Задачи по Катализу
Подождите немного. Документ загружается.


КАТАЛИЗ
4.2. Ферментативные процессы.
Задача 30. (M88). /C4.2.3/. Реакция, катализируемая ферментом E, протекает согласно следующей
схеме превращений:
PEESSE
21
1
kk
k
.
Определить период индукции. E
t=0
) =E
0
)
, S=) S.
Решение. Поскольку в практически интересных случаях концентрация субстрата значительно
превышает концентрацию фермента, индукционный период можно считать временем выхода на
стационарный режим τ
хар
. Методы оценки τ
хар
уже подробно обсуждались в задачах.
Поскольку S>>) E
0)
, при оценках можно считать концентрацию субстрата постоянной.
ESkESkSEk
dt
ESd
211
.
Существенным отличием от предыдущих задач является в данном случае необходимость
использовать уравнение массобаланса
0
EESE
, позволяющее свести кинетическое
уравнение к одной переменной:
ESbaESkkSkSEk
dt
ESd
211
0
1
.
Легко видеть, что
211
хар
kkSk
1
b
1
.
Задача 33. (M88). /C4.2.9/. Каталитическое разложение H
2
O
2
в водных растворах в присутствии
фермента каталазы (E) происходит по схеме:
1
k
k
22
EEOH
1
1
OH2OEOHE
22
k
221
2
,
в которой символом E
1
обозначен нестабильный интермедиат. Найти порядок реакции по
концентрации перекиси водорода и фермента. Найти скорость реакции при H
2
O
2
) =) 0,01) M;
k
1
)=)k
2
) =) 100) M
) –1)
c
–1
; k
–1
) =) 10
) –1)
c
–1
. Концентрацию фермента принять равной 10
) –7)
M.
Решение. Поскольку H
2
O
2
0
)>>)E
0)
, можно воспользоваться квазистационарным приближением:
0
22
ст
12
ст
11
ст
0
221
1
OHEkEkEOHk0
dt
Ed
.
Используя уравнение массобаланса по ферменту E+E
1
=E
0)
, преобразуем предыдущее выражение
к виду:
0OHEkEkEEOHk
0
22
ст
12
ст
11
ст
1
0
0
221
,
откуда находим стационарную концентрацию интермедиата
M10764
OHkkOHk
EOHk
E
8
0
2221
0
221
0
0
221
ст
1
,
.
Скорость разложения в стационарном режиме определяется необратимой второй стадией:
c
M
10764OHEkW
8
0
22
ст
12
,
.

4.3. Гомогенный катализ.
Задача 20. (М88 Катализ). /С4.3.5/. Гидролиз уксусного ангидрида (CH
3
CO)
2
O происходит при
взаимодействии с OH
) –
:
1. (CH
3
CO)
2
O)+)OH
) –
)→)CH
3
COOH)+)CH
3
COO
) –
, k
1
)=)10)M
) –1
·
)
с
–1
.
Катализатором гидролиза уксусного ангидрида является H
3
O
+
.
2. (CH
3
CO)
2
O)+)H
3
O
+
)→)(CH
3
CO)
2
OH
3
O
+
+
)
OH
2
) 2CH
3
COOH)+)H
3
O
+
.
Эффективная константа кислотного гидролиза k
2
равна 7·10
–3
M
) –1
·
)
с
–1
. При каком pH водного
раствора уксусный ангидрид будет наиболее устойчив?
Решение. Полная скорость гидролиза уксусного ангидрида является суммой скоростей по обоим
каналам реакции. Как следует из размерности константы скорости
11
cM
, эффективная скорость
реакции по каналу 2 зависит от концентраций (CH
3
CO)
2
O и H
3
O
+
, в то время как концентрация
воды H
2
O уже учтена в константе.
OCOCHOHkOHk
dt
OCOCHd
2
3321
2
3
.
Минимум скорости гидролиза, как легко видеть, соответствует минимуму выражения:
k
1)
OH
–
)+)k
2)
H
3
O
+
.
Продифференцируем его по H
3
O
+
, учитывая, что OH
–
H
3
O
+
)=)10
–14
М
) 2
.
0107
OH
10
10k
OH
OH
k
OH
OHkOHk
3
2
3
14
2
3
1
3
321
,
M1078310
7
1
OH
610
3
,
, pH)=)5,577.
Задача 1. (26.05.00 КР №3). /C4.3/. Найти выражение для стационарной скорости протекания
гомогенной каталитической реакции A)+)B)→)P, если ее механизм описывается схемой:
1.
XEA
1
1
k
k
2.
YH2X
a
K
3.
EH2PBY
3
k
.
Известно, что равновесия в первой и второй стадиях устанавливаются быстро, и константа
кислотной диссоциации Y равна K
a
.
Решение. Так как равновесие в первой и второй стадиях устанавливается быстро,
концентрации промежуточных продуктов X и Y можно рассчитать, исходя из
квазиравновесного приближения. Причем константа равновесия первой стадии является
отношением констант скорости прямой и обратной реакции:
1
1
1p
k
k
K
.
Таким образом
EA
X
K
1p
,
2
a
HX
Y
K
;
откуда получаем:
2
1pa
2
a
HEAKKHXKY
.

Стационарная скорость реакции, то есть скорость реакции после установления равновесия в 1-ой и 2-ой
стадиях (точнее квазиравновесия, так как 3-я стадия приводит к небольшому отклонению концентраций
X и Y от их равновесных значений, которым мы пренебрегаем) запишется в виде:
BHEAKKkBYkW
2
1pa33cт
.
4.4. Адсорбционные процессы и реакции на поверхности.
Задача 30. (М88 Катализ). /С4.4.4/. Адсорбция азота на слюде при 90)K хорошо описывается
изотермой Лэнгмюра. При давлениях 5 и 20 бар величина адсорбции (в мм
3
при стандартных условиях)
составляет 18 и 30 соответственно. Найти максимальное количество азота, которое может
адсорбироваться при этой температуре.
Решение. Изотерма Лэнгмюра позволяет определить степень заполнения поверхности θ как функцию
давления газа
2
N
P
2
2
Np
Np
PK1
PK
,
где K
p
– константа равновесия.
В свою очередь степень заполнения поверхности определяется как
m
n
n
,
где n – число заполненных адсорбционных мест, а n
m
– полное число адсорбционных мест, то
есть величина максимальной адсорбции.
Используя изотерму Лэнгмюра в виде
2
2
Np
Np
m
PK1
PK
nn
,
получаем два уравнения:
p
p
m
K51
K5
n18
,
p
p
m
K201
K20
n30
.
Решая, находим
pp
pp
KK5120
KK2015
30
18
,
K
p
) ≈) 0,175, n
m
) ≈) 38,57) мм
3
) н.у.
Задача 21. (М88 Катализ). /С4.4.5/. Энергия активации для прыжка из одной элементарной ячейки
поверхности в другую элементарную ячейку E
a
)=)20)ккал/моль. Оценить, на какое расстояние в
среднем сместится адсорбированная частица за 10)сек при T)=)400)K.
Решение. Для расстояния r, пройденного при случайном блуждании частицы на плоскости имеем
формулу Эйнштейна:
r
2
)=)t)·)4D,
где D)=)νl
2
– коэффициент диффузии частицы, определяемый произведением частоты прыжков ν на
квадрат длины прыжка l. Длину прыжка можно оценить, считая ее примерно равной межатомному
расстоянию, l≈2Å.
Частота ν рассчитывается, как произведение частоты тепловых колебаний на вероятность преодолеть
активационный барьер:
1
K400
Kмоль
кал
971
моль
кал
20000
34
23
RT
E
Б
c79e
cДж10636
40010381
e
h
Tk
акт
,
,
,
,
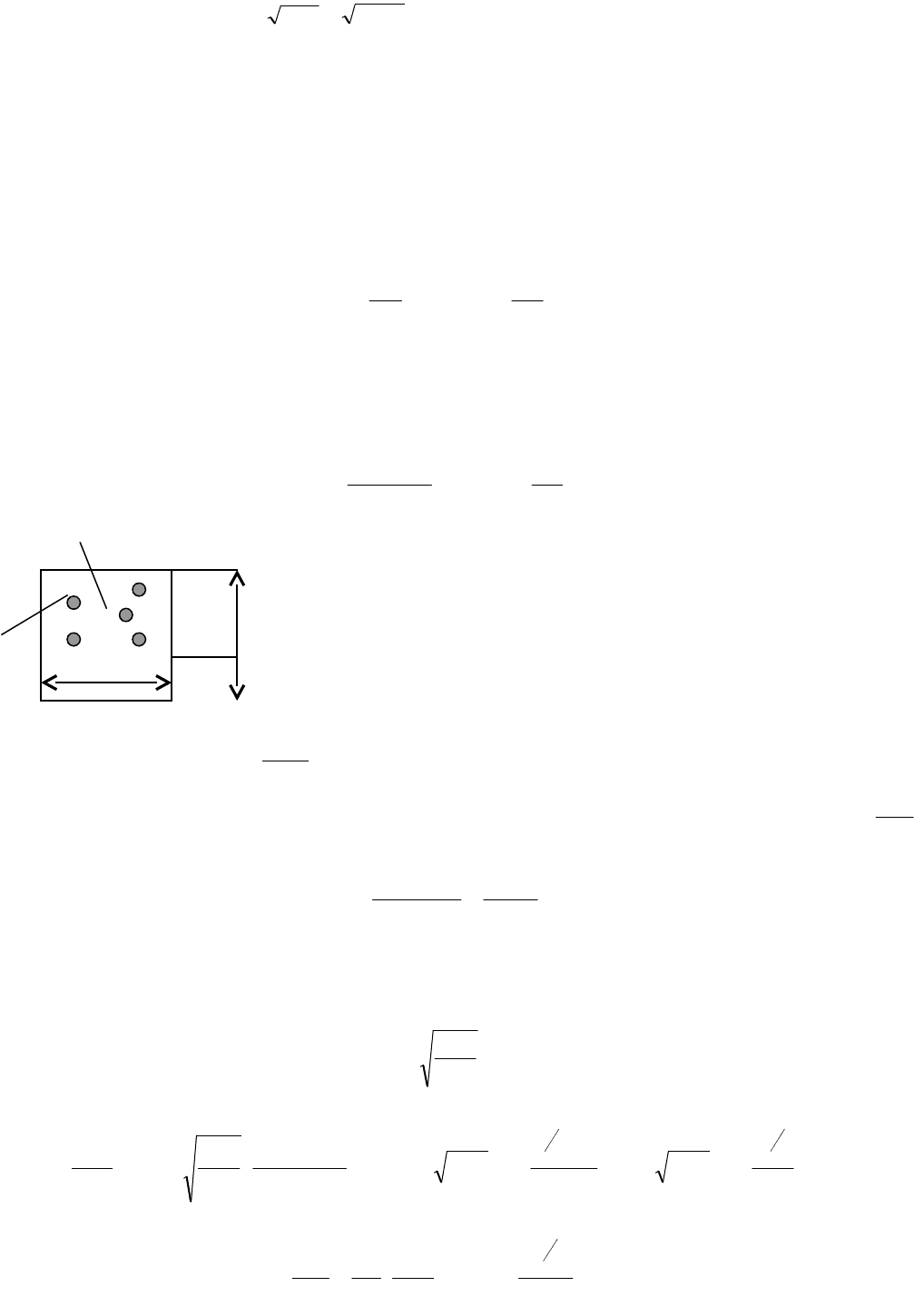
4112м101241tl4Dt4r
82
,,
Å .
Задача 5. (М88 Катализ). /С4.4.14/. На однородной поверхности протекает бимолекулярная
реакция A) +) B) →) C(газ). Частицы B расположены на поверхности в виде непересекающихся
островков одинакового радиуса, остальная часть поверхности занята частицами A . Реакция
протекает на границах островков в кинетическом режиме, то есть реакция не лимитируется
диффузией частиц A к островкам. Найти зависимость покрытия (θ
A)
, θ
B
) поверхности
реагентами от времени.
Решение. Выразим степень покрытия поверхности как
0
A
A
N
N
,
0
B
B
N
N
,
где N
A
и N
B
– число частиц на единице поверхности, N
0
– число адсорбционных мест на
единице поверхности. Внутри островков покрытие монослойное, то есть все адсорбционные
места заняты частицами B. В начальный момент времени
0
B
0
A
NN
, то есть
0
B
0
A
.
Пусть на единице поверхности находится m
B
островков частиц радиуса r, тогда
0
B
B
2
0
B0
2
B
N
N
mr
N
mNr
.
A
1
B
1
Скорость исчезновения частиц описывается выражением
BA
B
mrn2k
t
N
, (*)
где k – константа скорости реакции, n
A
– реальная (в отличие от кажущейся концентрации
1
N
A
)
концентрация частиц A на поверхности.
B
A
B
2
A
A
1
N
mr1
N
n
.
Далее, исходя из равенства
θ
B
) =) πr
2
m
B)
,
находим
B
B
m
r
.
Используем очевидное соотношение θ
A
) =) θ
B
(в любой момент времени) и подставляем в (*):
1
Nmk2
1
Nmk2m
1N
NN
m
2k
t
N
2
3
B
0B
B
A
2
1
B
0BB
B0
0A
B
BB
.
Таким образом,
B
2
3
BB
0
B
1
const
dt
dN
N
1
t
.

Задача 17. (М88 Катализ). /С4.4.17/. Титрование адсорбированного на поверхности металла кислорода
водородом при давлении
Па10P
6
H
2
идет по схеме:
H2газH
1
1
k
k
2
(1)
OHHO
3
k
(2)
газOHHOH
2
k
4
, (3)
молекулы газовой фазы отмечены индексом (газ), остальные частицы адсорбированы. Кинетические
уравнения, соответствующие стадиям (1) - (3), имеют вид
HOH4HO3
2
H1H1
2
t
H
kkkPk1
dt
d
2
,
HO3
O
k
dt
d
,
HOH4HO3
OH
kk
dt
d
,
где
2
H
P
– давление водорода, θ
t
)=)θ
O
)+)θ
H
) +) θ
OH
– полное покрытие, )k
1
)=)10
6
)Па
–1
·с
–1
,
k
-1
)=)1)с
–1
, k
3
)=)10
4
)с
–1
, k
4
)=)10
6
)с
–1
.
Начальные условия при t) =) 0: θ
O
)=)0,9, θ
H
) =) θ
OH
) =) 0. Найти за какое время покрытие
поверхности кислородом достигнет величины θ
O
)=0,1.
Решение. Предложенная кинетическая схема является нелинейной, и не позволяет интегрирование в
аналитическом виде, поэтому необходимо использовать упрощение. Например, предположим, что
применим метод квазистационарных концентраций и проверим это предположение. Для этого найдем в
квазистационарном приближении θ
H
и θ
OH
(попутно сразу предполагая, что они много меньше θ
O)
:
θ
H)
,θ
OH
)<<)θ
O
, 1)-)θ
t
)≈)θ
O
).
HOH4HO3
2
H1H1O
H
kkkPk0
dt
d
2
,
HOH4HO3
OH
kk0
dt
d
.
Решая систему алгебраических уравнений, получаем:
0k2kPk
HO3
2
H1H1
2
O
2
,
090102101090
2
HH
466
2
,,
,
θ
H
=4,5·10
–5
,
3
O
4
3
OH
109
k
k
.
Так как θ
H
и θ
OH
действительно очень малы, то можно использовать их квазистационарные значения,
и наше предположение оправдано.
Скорость десорбции H
2
пренебрежимо мала по сравнению со скоростью рекомбинации H и O:
HO3
2
H1
k2k
,
поэтому можно записать
0k2Pk
dt
d
HO3H1
2
O
H
2
,
O
5
O
3
H1
H
105
k2
Pk
2
,
OO
54
HO3
O
5010510k
dt
d
,
,
t50
O
e90
,
,
,
c394
10
90
50
1
t
10
,
,
,
ln
,
,
.
Задача 19. (М88 Катализ). /С4.4.18/. Двухатомная молекула может при адсорбции ориентироваться
параллельно поверхности, занимая два места, и перпендикулярно, занимая одно адсорбированное
место. В духе модели Лэнгмюра вывести уравнение изотермы адсорбции.

Решение. В духе модели Лэнгмюра обозначим как θ
1
места, где молекулы адсорбированы
перпендикулярно поверхности, а как θ
2
– места с параллельной адсорбцией. Заметим, что θ
2
соответствует двум местам на поверхности, поэтому условие массобаланса по полному числу мест
выглядит следующим образом
θ
1
) +) 2θ
2
) +) θ=1,
где θ – число незаполненных адсорбционных центров.
Пусть константы адсорбции и десорбции для простоты равны 1. Тогда получаем систему
уравнений на θ
1
и θ
2
:
0P
dt
d
1
1
,
0P11
dt
d
2
4
2
.
Приведем объяснение, как получено второе уравнение. Первое слагаемое описывает вероятность найти
два свободных адсорбционных центра рядом, которая является произведением вероятности найти
свободное место θ на вероятность того, что рядом с этим местом есть еще одно свободное:
(1) –(1) –) θ)
4
). В свою очередь, эта величина получается, если мы предположим, что решетка
квадратная и каждое адсорбционное место имеет четыре соседа. Тогда ( 1) –) θ)
4
– вероятность,
что все четыре места заняты, а 1) –) (1) –) θ)
4
– вероятность найти одно или более свободных
мест.
Итак,
θ
1
) =) θΡ, θ
2
=θ(1) –) (1) –) θ)
4
)Ρ,
или
θ
2
=θ
1)
(1) –(1) –) θ)
4
).
Подставляя θ
1)
, θ
2
в условие массобаланса, находим:
θΡ) +) 2θ) (1) –) (1) –) θ)
4
)Ρ) +) θ=) 1,
θ) (3Ρ) –) 4θ) +) 6θ
2
–) 4θ
3
+) θ
4
)) =) 1.
Дальше автору этих строк продвинуться не удалось.
Задача 31. (М88 Катализ). /С4.4.23/. Оценить теплоту адсорбции криптона на древесном угле,
используя следующие величины количества адсорбированного газа (в единицах 10
13
)мол/см
2
)
T,)K 5тopр 15тopр
273,2 0,7 2,0
193,5 3,9 7,6
При оценке пользоваться изотермой Лэнгмюра. Оценить стандартную энтропию адсорбции.
Решение. Чтобы рассчитать теплоту адсорбции, необходимо знать зависимость константы
адсорбционного равновесия K от температуры. Рассчитаем K по данным задачи, используя изотерму
адсорбции Лэнгмюра (см. также задача??(30)):
KP1
KP
nn
m
.
Получаем четыре уравнения:
273
273
m
13
K51
K5
n1070
,
,
273
273
m
13
K151
K15
n102
,
193
193
m
13
K51
K5
n1093
,
,
193
193
m
13
K151
K15
n1067
,
.
Откуда
K
273
)=)0,012)торр
–1
, K
193
)=)0,092)торр
–1
.
Зная температурную зависимость, воспользуемся уравнением изобары химической реакции (см. курс
химической термодинамики ??)
2
RT
H
T
K
ln
,
2273
1
5193
1
R
H
K
K
193
273
,,
ln
,

моль
кДж
211H ,
,
где ΔH – искомая теплота сорбции.
Задача 9. (М88 Катализ). /С4.4.30/. Под действием рентгеновского излучения в атмосфере кислорода
на поверхности твердого тела образуется короткоживущие активные центры A* хемосорбции
кислорода:
AO
2
A*
A
Считая, что хемосорбция при T)=)500˚C протекает по механизму Или-Ридила с коэффициентом
прилипания p)=)10
–1
, определить зависимость начальной скорости хемосорбции W
хем
от давления
кислорода
2
O
P
и оценить значения W
хем
при
2
O
P
)=)100)торр и 10
–6)
торр. Время жизни активных
центров 10
–3
с, скорость их образования 3·10
10)
см
–2
·c
–1
. Состояние A неактивно в процессе
хемосорбции.
Решение. Поскольку процессы образования и гибели активных центров A* быстропротекающие,
рассмотрим задачу в стационарном приближении:
0OAkAkW
dt
Ad
2
ст
2
ст
10
,
где W
0
)=)3·10
10
см
–) 2
·с
–1
– скорость образования активных центров,
13
3
1
c10
c10
1
k
–
константа скорости дезактивации A*, k
2
– константа скорости хемосорбции O
2
, которую
необходимо оценить из молекулярно-кинетической теории газов. Величина k
2
A*
ст
по
физическому смыслу является вероятностью прилипания молекулы кислорода в единицу
времени к единичной площадке поверхности. В свою очередь она распадается на произведение
вероятностей достигнуть поверхности и вероятности, что данный участок является активным
центром A*.
Очевидно, что поверхности за 1) с достигнут все молекулы O
2
, которые движутся в
нужном направлении и находятся на расстоянии, меньшем средней тепловой скорости
с
см
10157
с
м
715
m
Tk8
4
Б
,
. Так как все направления движения равновероятны, то
количество таких молекул
6
. Точный расчет, учитывающий распределение молекул по
скоростям, дает результат
4
(см??). Чтобы найти долю поверхности, занятую A*, необходимо
оценить площадь активного центра σ. Предположим, что она приблизительно равна сечению
молекулы кислорода, то есть
σ≈) 20Å
2
) =) 2·10
–15
см
2
.
Тогда
с
см
10573
4
10210k
3
12151
2
,
.
Количество активных центров составляет
2
3
Б
0
21
0
221
0
ст
cм
1
1086
Tk
P
kk
W
Okk
W
A
2
,
;
2
7
см
1
103
при давлении 100) торр и 10
–6
торр, соответственно.
Скорость хемосорбции в этих случаях будет
+O
2
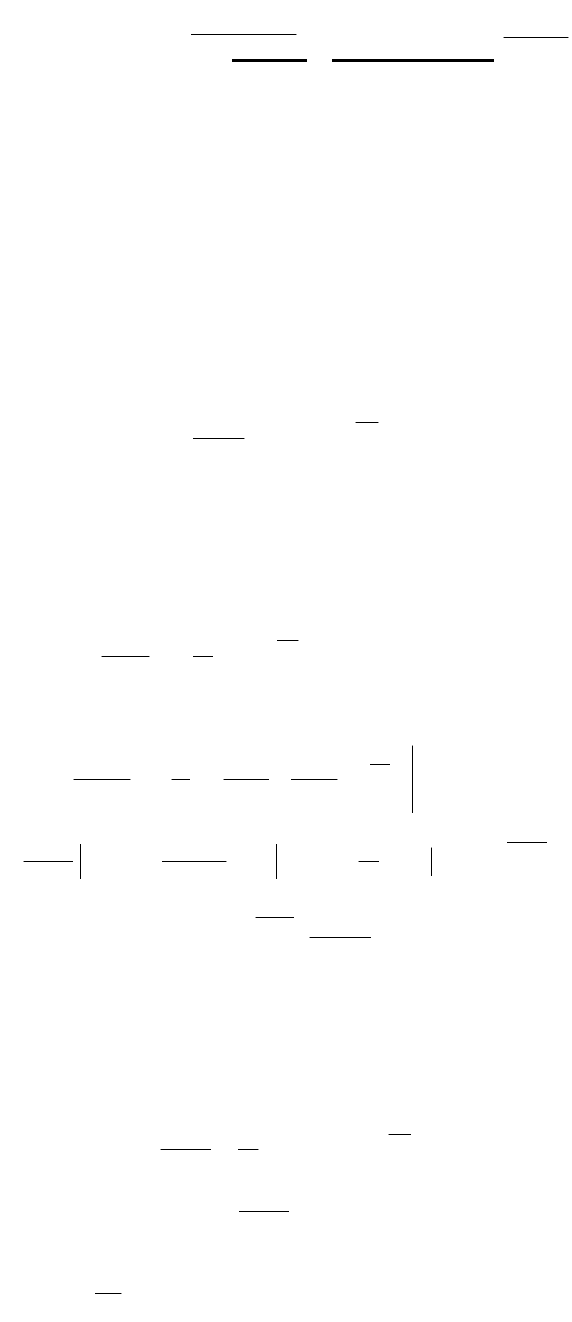
10
221
22
2
ст
2хем
103
Okk
Ok
OAkW
;
ссм
1
10321
2
6
,
.
Отметим, что в первом случае большинство активных центров реагирует с кислородом, в то
время как при малом давлении A* в основном дезактивируются.
Задача 1. (23.09.99 Канд. экз.). /С4.4/. Линейный во времени нагрев монокристалла с адсорбированным
на его поверхности веществом А приводит к десорбции последнего в хорошо откачиваемый вакуумный
объем. Скорость десорбции анализируется масспектрометром в непосредственной близости от
поверхности монокристалла. Как изменится (увеличится или уменьшится) температура максимума
десорбционной кривой при изменении скорости нагрева, если известно, что вещество А десорбируется
по первому порядку? (Обосновать предполагаемую тенденцию).
Решение. Воспользуемся (Боресков???) следующей формулой для кинетики десорбции A:
RT
E
eA
dt
Ad
,
где A – концентрация на поверхности монокристалла, Е – энергия активации десорбции, β –
постоянный коэффициент. Скорость нагрева линейно зависит от времени
Т)=)Т
0
)
+)α)t,
здесь Т – температура монокристалла в момент времени t, Т
0
)
– начальная температура, α – скорость
нагрева. Выражая t через T и подставляя в предыдущее выражение, получаем:
RT
E
eA
dT
Ad
, (*)
откуда находим положение max, анализируя вторую производную от поверхностной
концентрации A:
0e
RT
E
dt
Ad
dT
Ad
TT
RT
E
22
2
max
,
max
max
maxmax
max
RT
E
TT
TT
2
TT
eAA
RT
E
dt
Ad
,
E
RT
e
2
RT
E
max
max
.
Из последней формулы легко видеть, что увеличение α должно сопровождаться увеличением
Т
max
. В принципе, этого достаточно для правильного ответа на поставленный вопрос: при
возрастании скорости нагрева максимум смещается в область более высоких температур.
Однако, приведем, следуя оригинальному решению задачи, также дополнительные выкладки,
подтверждающие этот вывод.
RT
E
1
eTA
dT
Ad
.
Появление max на кривой термодесорбции
Тот
dt
Ad
обусловлено уменьшением поверхностной
концентрации вещества А в процессе нагрева A(Т) и одновременным увеличением вероятности
десорбции (пропорциональной
RT
E
e
).
Рис.???
Пусть при определенной скорости нагрева max находится при Т
max
. Увеличивая скорость нагрева
можно добиться того, что концентрация А при Т) =Т
max
)
будет сколь угодно близка к начальной
A
0
.
(Вещество не будет успевать десорбироваться).

В этом случае можно полагать A(Т
1max
α))≈)A
0
. Правая часть уравнения будет выглядеть
RT
E
0
eA
и расти с температурой при Т) =Т
max.
. То есть при увеличении скорости нагрева
температура максимума должна сдвинуться в область более высоких температур.
Задача 4. (весна 1999 Канд. экз.). /С4.4/. На поверхности цеолитного катализатора присутствуют два
вида адсорбционных центров молекул диоксида хлора. Найти равновесную долю активных центров
каждого вида, занятых молекулами ClO
2
, если константы адсорбционного равновесия для активных
центров первого и второго вида связаны соотношением (К
1)
/К
2
)) =)4, а половина общего числа
активных центров катализатора в равновесии свободна. Концентрации активных центров первого и
второго типов на поверхности одинаковы.
Решение. Данная задача описывается следующей системой реакций и соответствующих кинетических
уравнений:
1
1
S
2
K
12
ClOSClO
,
1
ClO12
1
ClO1
1
ClO
22
2
KClO1K
dt
d
,
2
2
S
2
K
22
ClOSClO
,
2
ClO22
2
ClO2
2
ClO
22
2
KClO1K
dt
d
.
Для решения задачи воспользуемся изотермой адсорбции Лэнгмюра, которая легко получается из
кинетических уравнений, если приравнять нулю правые части, то есть рассматривать равновесный
случай.
21
21
1
ClO
ClOK1
ClOK
2
,
22
22
2
ClO
ClOK1
ClOK
2
,
где
1
ClO
2
,
2
ClO
2
степени заполнения 1-го и 2-го типов адсорбционных центров, соответственно;
ClO
2
– концентрация диоксида хлора в газовой фазе, К
1
и К
2
– константы соответствующих
адсорбционных равновесий. Находя из изотерм ClO
2
и приравнивая эти выражения, получаем
уравнение на
1
ClO
2
и
2
ClO
2
:
2
ClO2
2
ClO
1
ClO1
1
ClO
2
2
2
2
2
1K1K
ClO
,
или
2
2
ClO
2
2
ClO
1
ClO
1
ClO
2
ClO
2
ClO
2
1
2
2
2
2
2
2
1
1
1
K
K
4
. (1)
Поскольку половина общего числа активных центров свободна, получаем еще одно уравнение:
111
2
ClO
1
ClO
22
,
1
2
ClO
1
ClO
22
. (2)
Решая систему уравнений (1) и (2), находим долю занятых активных центров второго вида:
012
2
ClO
2
ClO
2
2
2
,
21
2
ClO
2
,
40
2
ClO
2
,
,
(второй ответ не подходит, так как должно быть
)≥)0);
60
1
ClO
2
,
.
Задача 5. (14.04.98 Канд. экз.). /C4.4/. Одной из причин дезактивации нанесенных металлических
катализаторов является «спекание». Этот термин означает, что за счет поверхностной диффузии
или диффузии через газовую фазу происходит перенос атомов металла от мелких частиц (зерен) к
крупным. В англоязычной литературе такой процесс называется «Ostwald ripening». Классическая
теория асимптотического роста зерен была построена Лифшицем и Слезовым в начале 60-х годов.
Согласно их теории, увеличение среднего радиуса зерен со временем описывается уравнением
dr/dt)=)A/r
2
, (1)

где А – константа, пропорциональная коэффициенту диффузии.
Предполагая, что (а) форма каталитических частиц близка к сферической, (б) средний размер
частиц удовлетворяет уравнению (1), и (с) активность отдельной частицы катализатора
пропорциональна ее поверхности, получить зависимость наблюдаемой активности катализатора
(т.е. активности на макроскопическую единицу объема) от времени. Предполагая, что за 10 дней
наблюдаемая активность уменьшится в два раза, определить, за какое время активность уменьшится
в четыре раза (по отношению к начальной активности).
Решение. Пусть в единице объема содержится m
r
металла (частицы радиуса r, плотность
–
const). Следовательно, количество зерен катализатора N может быть найдено из уравнения:
r
3
mrNr
3
4
,
3
r
3
4
m
rN
.
А их поверхность рассчитывается как
r
m3
r
3
4
m
r4Nr4rS
3
22
.
Найдем скорость изменения площади поверхности в единице объема:
4222
r
Am3
r
A
r
m3
dt
dr
r
m3
dt
dS
.
Изменение среднего радиуса зерна рассчитывается интегрированием уравнения Лифшица-
Слезова:
dr/dt)=)A/r
2
,
, AtRR
3
1
AdtdRR
3
0
3
t
0
R
R
2
0
3
0
3
RAt3R
.
Теперь легко определить зависимость активности катализатора от времени.
3
1
3
0
RAt3
m3
tS
.
Обозначим как S
0
и R
0
исходные поверхность и средний радиус частиц, S
10
поверхность
катализатора через 10 дней, и рассчитаем, следуя оригинальному решению, время уменьшения
активности в 4 раза.
0
0
R
m3
S
,
2
R
R10A3
S
S
0
3
1
3
0
10
0
,
3
1
3
0
10
R10A3
m3
S
,
8
R
R10A3
3
0
3
0
.
3
1
3
0
4
1
X
RAt3
m3
S
,
644
R
RAt3
S
S
3
3
0
3
0
3
4
1
0
,
3
0
3
0
R
R10A3
.
8
R10A3
RAt3
S
S
3
0
3
0
3
4
1
10
,
8
1
R10A3
R
3
0
3
0
,
64
R
RAt3
3
0
3
0
.
81
R
10A3
3
0
,
641
R
tA3
3
0
,
10
7
R
A3
3
0
,
641t
10
7
.
90
7
1063
t
дней.
Задача 3. (14.04.98 Канд. экз.). /C4.4/. Первой стадией приготовления нанесенных катализаторов
часто является стадия закрепления предшественника активного компонента на поверхности
носителя путем взаимодействия с поверхностными функциональными группами.
Напишите возможные химические реакции, протекающие при сорбции TiCl
4
из неводных растворов на
поверхности SiO
2
и MgO.
