Задачи на скрещивающиеся прямые. Алгоритмы решения
Подождите немного. Документ загружается.

Глава 1. Скрещивающиеся прямые. Основные понятия.
1. Скрещивающиеся прямые. Определение.
Как известно из планиметрии, для двух прямых на плоскости
возможны два случая их взаимного расположения: либо эти прямые
пересекаются, либо они параллельны.
Поскольку в пространстве имеются плоскости, и на них
выполняется планиметрия, то эти два случая взаимного расположения
прямых сохраняются и для пространства. Но в пространстве
добавляется еще один случай – когда две прямые не лежат в одной
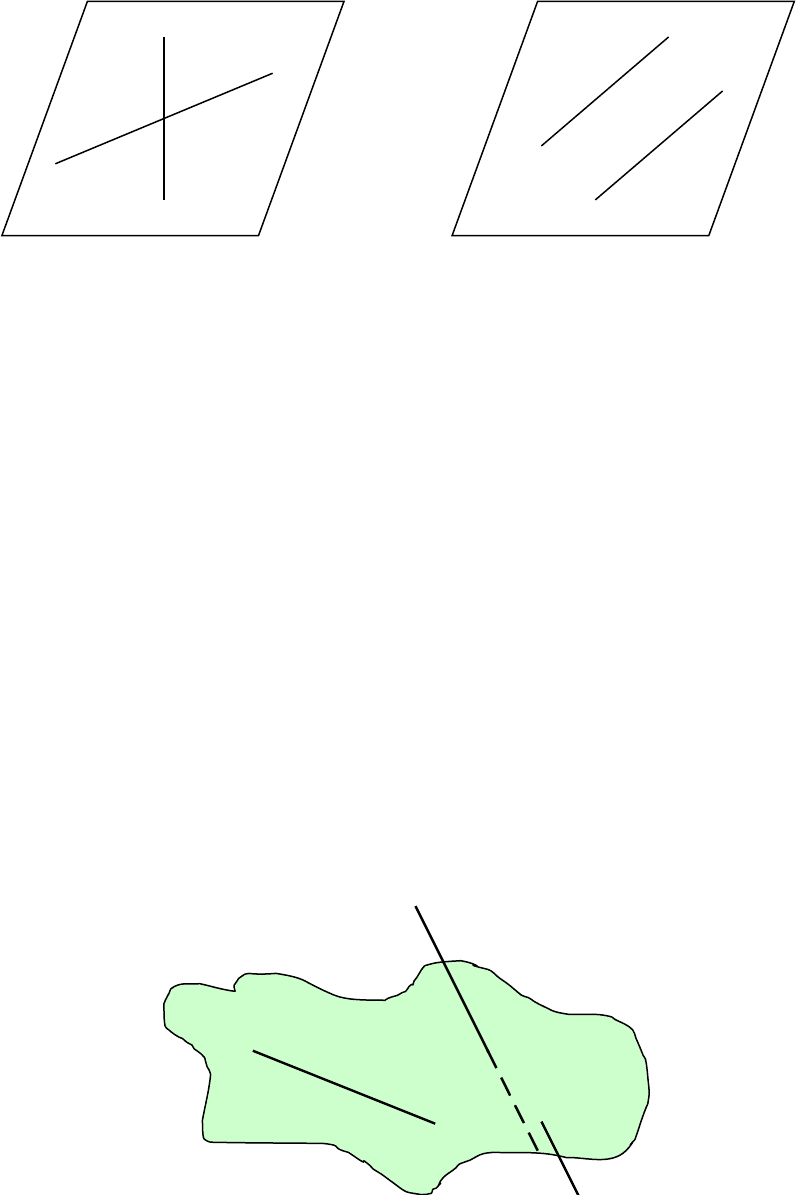
плоскости. Такие две прямые легко построить. Возьмем любые четыре
точки A, B, C, D, не лежащие в одной плоскости. Тогда прямые AB и
CD не лежат в одной плоскости.
D
А
C
В
a
b
a b
A
a C b’
b’
a’
B b D
α
Определение: Две прямые, не лежащие в одной плоскости,
называются скрещивающимися.
Иначе говоря, скрещивающиеся прямые – это прямые, через которые
нельзя провести плоскость.
2. Способы нахождения расстояния между скрещивающимися
прямыми.
Для нахождения расстояния между скрещивающимися прямыми
существуют четыре основных способа:
1. нахождение общего перпендикуляра двух скрещивающихся
прямых;
2. расстояние от одной из скрещивающихся прямых до
параллельной плоскости, проходящей через другую прямую;
3. нахождение расстояния между параллельными плоскостями, в
которых находятся скрещивающиеся прямые;
4. нахождение расстояний между проекциями скрещивающихся
прямых на перпендикулярную им плоскость.
Для начала докажем, что две скрещивающиеся прямые имеют
общий перпендикуляр, и притом только один. Он является общим
перпендикуляром параллельных плоскостей, проходящих через эти
прямые.
Определение: Общим перпендикуляром двух скрещивающихся
прямых называется отрезок с концами на этих прямых и являющийся
перпендикуляром к каждой из них.
α
β

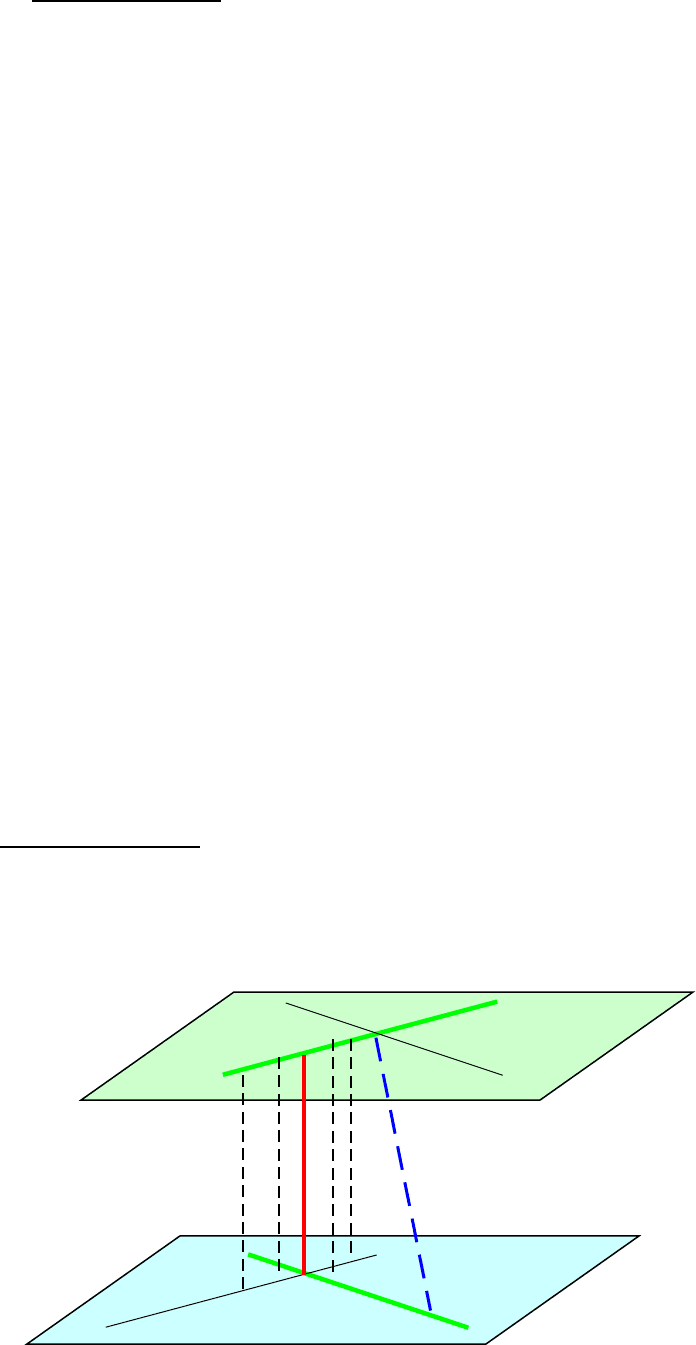
Доказательство: Действительно, пусть a и b – данные
скрещивающиеся прямые. Проведем через них параллельные
плоскости α и β. Прямые, пересекающие прямую а и
перпендикулярные плоскости α, лежат в одной плоскости. Эта
плоскость пересекает плоскость β по прямой a’,параллельной а. Пусть
В – точка пересечения прямых a’ и b. Тогда прямая АВ,
перпендикулярная плоскости α, перпендикулярна и плоскости β, то
есть, β параллельна α. Отрезок АВ – общий перпендикуляр
плоскостей α и β, а значит и прямых а и b.
Теперь докажем, что этот перпендикуляр единственный.
Допустим, что у прямых a и b есть другой общий перпендикуляр СD.
Проведем через точку С прямую b’ параллельную b. Прямая СD
перпендикулярна прямой b, а значит и b’.Так как она
перпендикулярна прямой а, то она перпендикулярна плоскости α, а
значит параллельна АВ. Выходит, что через прямые АВ и СD, как
через параллельные, можно провести плоскость. В этой плоскости
будут лежать наши скрещивающиеся прямые АС и ВD, а это
невозможно, что и требовалось доказать.
Определение: Расстоянием между скрещивающимися прямыми
называется длина их общего перпендикуляра. Оно равно расстоянию
между параллельными плоскостями, проходящими через эти прямые.
L b
A
a K
В
a’
Глава 2. Алгоритм нахождения расстояния между
скрещивающимися прямыми.
1.Случай, если одна из прямых лежит в плоскости основания.
Рассмотрим случай, когда одна из прямых лежит в плоскости
основания.
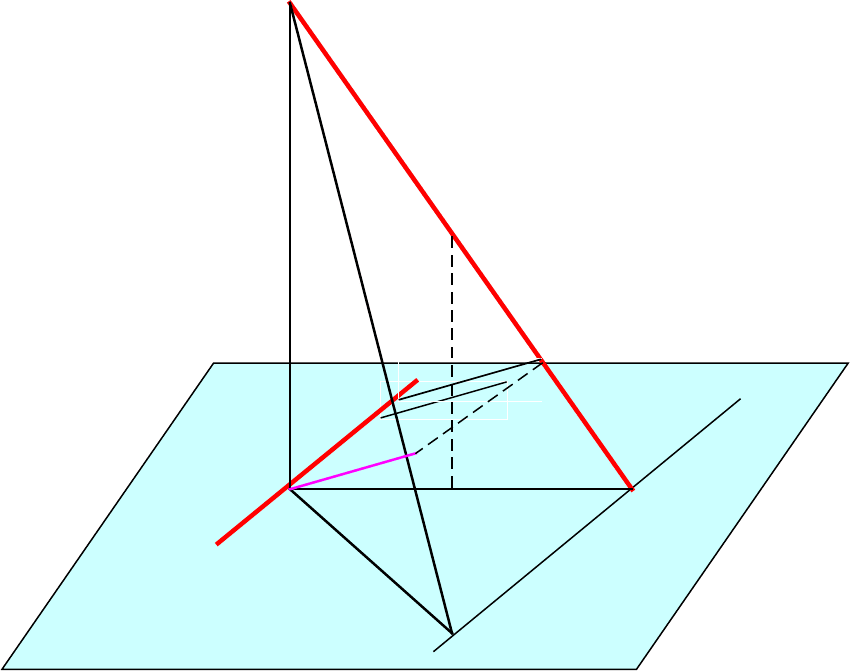
Пусть даны две скрещивающиеся прямые a и b .Прямая а лежит
в плоскости α, а прямая пересекает b плоскость α в некоторой точке
В. Найти расстояние между прямыми а и b.
P
М
В
α С
Порядок выполнения работы.
1. Возьмем произвольную точку М, принадлежащую прямой b.
2. Из точки М опустим перпендикуляр МК на плоскость α , точка К
принадлежит α.
3. Проведем прямую ВК, которая пересекает прямую а в некоторой
точке А.
4. Через точку В проведем прямую а’ параллельную а.
5. Восстановим из точки А перпендикуляр АР к плоскости α, АР
пересечет b в точке Р.
6. Из точки А на прямую а’ опустим перпендикуляр АС.
7. Рассмотрим прямоугольный треугольник РАС. Проведем из
точки А перпендикуляр АL на гипотенузу PС.
Перпендикуляр АL является искомым. Докажем это.
c B1
B2
Доказательство:
По построению АL перпендикулярна РС. Так как АС является
проекцией АL на α , то по теореме о трех перпендикулярах АL
перпендикулярна a’.Отсюда, по признаку перпендикулярности прямой
и плоскости АL перпендикулярна плоскости (ВРС), а значит она
перпендикулярна любой прямой, лежащей в этой плоскости, AL
перпендикулярна b.
2. Случай, когда одна из прямых перпендикулярна плоскости
основания.
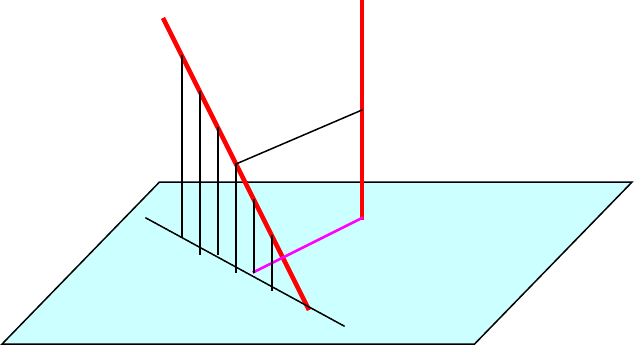
Пусть даны две скрещивающиеся прямые а и b. Прямая а
перпендикулярна плоскости α. Найдем расстояние между этими
прямыми.
b a
A2 A1
α
Порядок выполнения работы.
1. Так как плоскость α перпендикулярна прямой а, то
ортогональная проекция последней на α есть точка В1
пересечения α и а.
2. Искомое расстояние между а и b равно расстоянию от В1 до
прямой с, где с – ортогональная проекция b на α.
3. Пусть В1В2 перпендикуляр, опущенный в плоскости α из точки В1
на прямую с.
Докажем, что В1В2 – искомое расстояние.
Доказательство:
Точка В2, принадлежащая прямой с является ортогональной
проекцией на α в некоторой точке А2, принадлежащей b, откуда
А2В2 перпендикулярна В1В2. По признаку перпендикулярности
прямой и плоскости, отрезок В1В2 перпендикулярен плоскости π,
A
содержащей прямые b и с (а значит и отрезок А2В2). Очевидно, что
а параллельна π.
Следовательно, отрезок В1В2 есть перпендикуляр, опущенный из
точки В1, принадлежащей а, на плоскость π, проходящую через b
параллельно а, и его длина и есть расстояние между а и b.
Глава 3. Как применять алгоритмы нахождения
расстояния между скрещивающимися прямыми на
практике.
Задача 1.
В кубе с ребром а найти расстояние между непересекающимися
диагоналями двух смежных граней.
Решение:
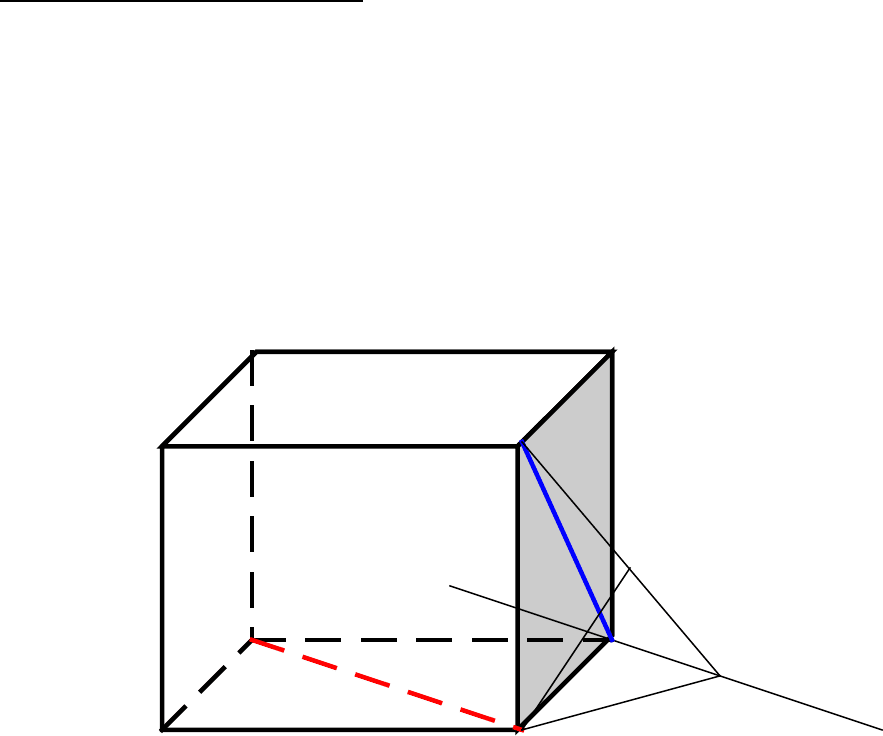
Обозначим через АВСDА1В1С1D1 куб. Нужно найти расстояние
между диагональю основания АС и диагональю боковой грани
С1D1.
1 способ (по алгоритму 1).
1. Через точку D проведем прямую а1 параллельную АС.
2. Проведем перпендикуляр СЕ из точки С на прямую а1.
3. Рассмотрим прямоугольный треугольник С1СЕ. Из точки С
проведем высоту СL, СL перпендикулярна С1Е.
С – искомое расстояние между АС и С1.
A1 D1
B1 C1
L
D E
a1
A
B C
Как высота из прямоугольного треугольника С1СЕ,
CC1∙CE
3
СL = ───── = a∙───.
C1E 3
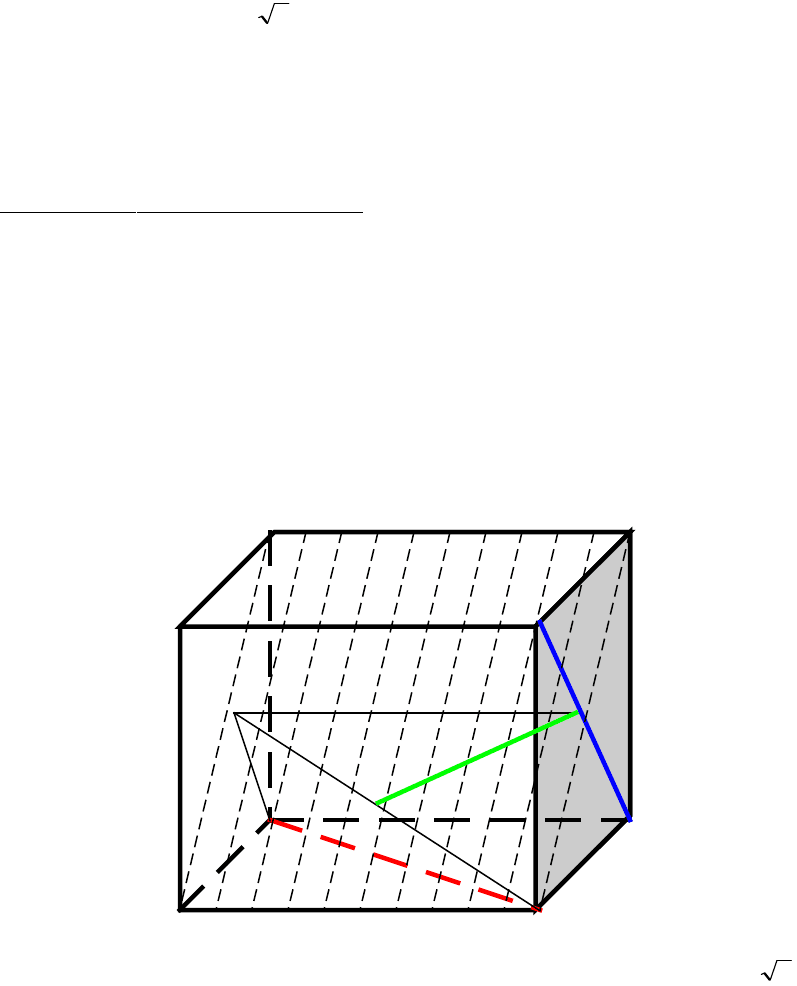
2 способ ( по алгоритму 2).
1. Выбрав две прямые СD1 и А1В строим плоскость π,
перпендикулярную DС1.
2. Проекция DC1 на π – С’,АС – А1С, где АА1 – перпендикуляр к π.
3. Из точки С’ восстанавливаем перпендикуляр к А’C, C’K – искомое
расстояние.
A1 D1
B1 C1
A' C’
K D
B C
A’C’∙CC’
3
Из треугольника А’С’С, С’К = −−−−−−− = a∙−−.
A’C 3
Задача 2.
Дана правильная треугольная призма со стороной основания а и
высотой Н. Найти расстояние между высотой основания и
непересекающейся с ней апофемой боковой грани.
Решение:
Пусть SABC – данная пирамида. Найдем расстояние между
высотой основания BL и апофемой SD боковой грани SBC.
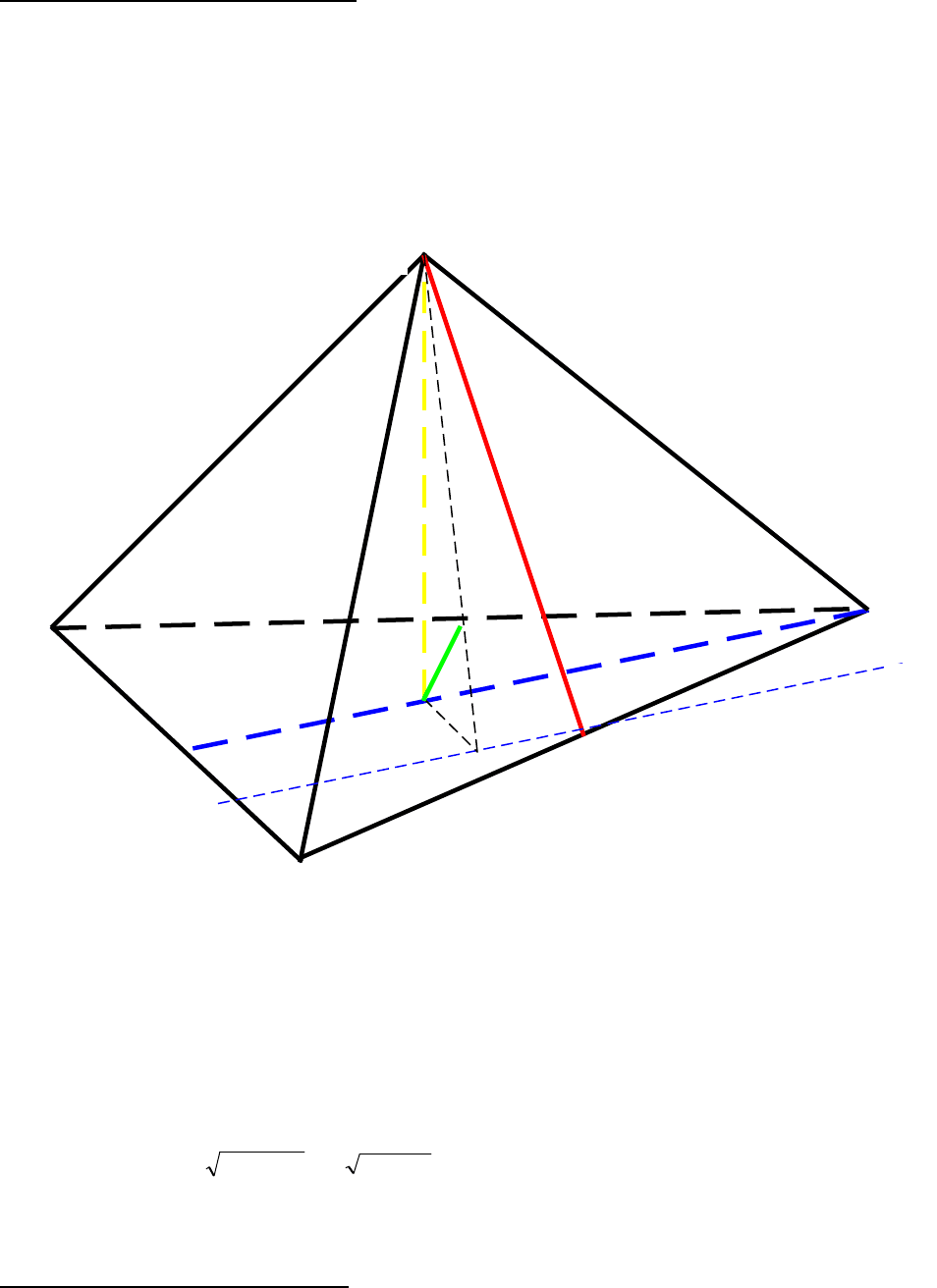
1 способ (по 1 алгоритму).
1. Через точку D проведем прямую a1 ,параллельную BL.
2. Опустим перпендикуляр SO на плоскость основания АВС.
3. Из точки О проведем перпендикуляр ОЕ к прямой а1.
4. Рассмотрим прямоугольный треугольник SOE:ОК перпендикулярно
SE, ОК – искомое расстояние.
SO∙OE h∙a/4 a∙h
OK = −−−−− = −−−−−− = −−−−−
SE
16/ah
ah 16
2 способ (по 2 алгоритму)
1. Из точки S восстановим перпендикуляр SO к плоскости (АВС).
2. Через точку О проведем прямую а, параллельную АС.
3. Поскольку BL перпендикулярно АС, то она перпендикулярна и а.
Через точку S и прямую а построим плоскость, перпендикулярную
BL.
E
A
K
O
L
B
D
a
C
S
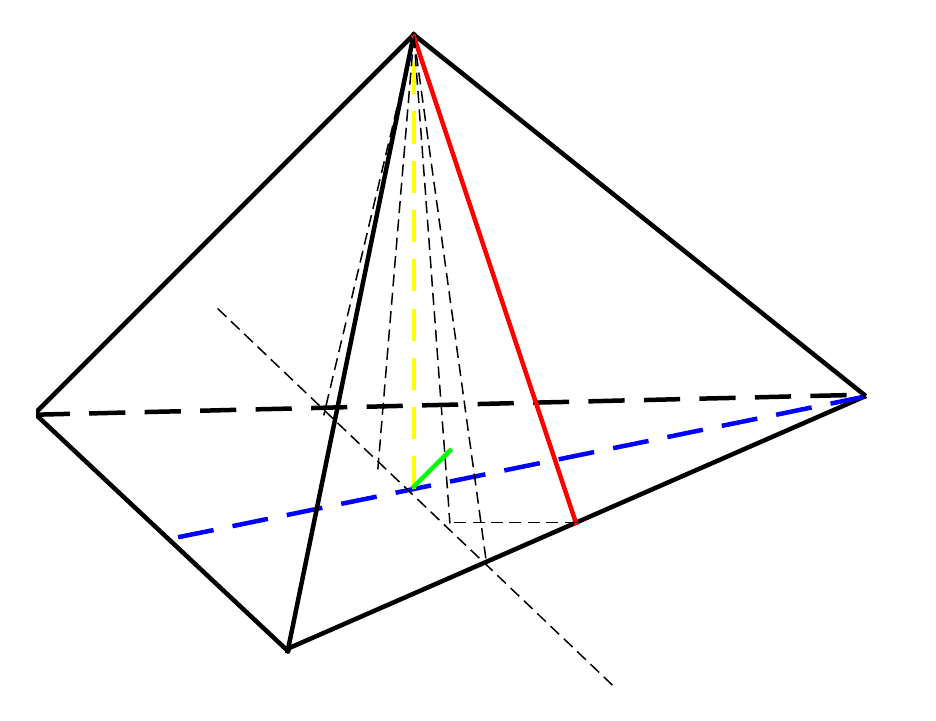
4. Точка О – проекция BL на эту плоскость, SD’ – проекция SD на эту
плоскость.
5. Из точки О опустим перпендикуляр на SD’, OH – искомое
расстояние.
OH находится из треугольника SOD’ так же, как в 1 случае.
D
H
D’
O
a
S
L
A
C
B
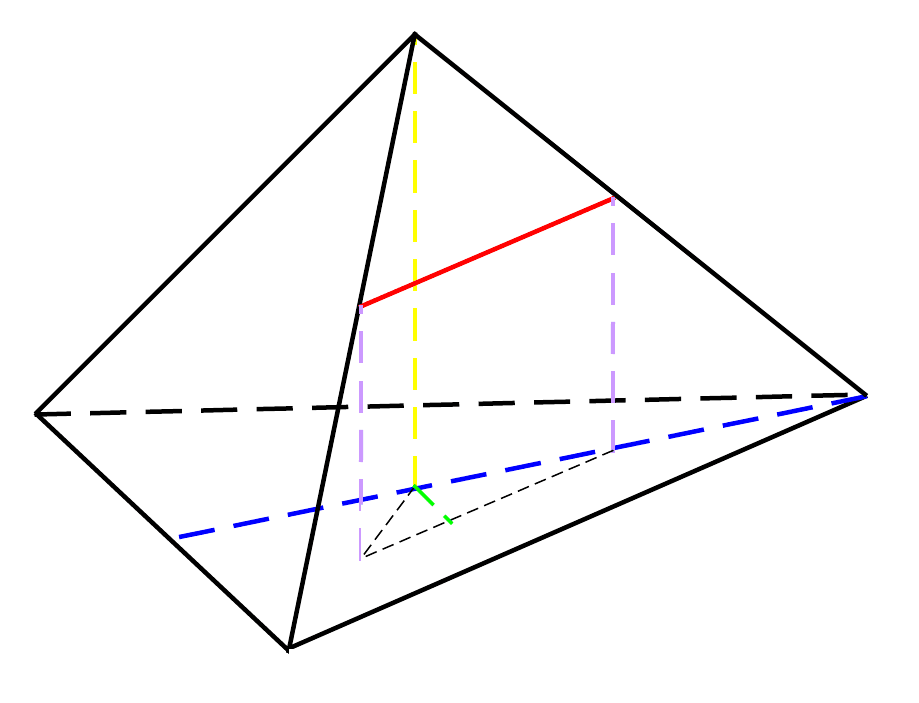
Задача 3.
Дана правильная треугольная пирамида SABC со стороной основания
а. На ребре SB взята точка Е, которая делит SB в отношении k, а на
ребре SC взята точка D, которая делит SC в отношении m. Найти
расстояние между высотой основания BN и отрезком DE.
Решение:
Выполним дополнительные построения:
1. Из точки Е опустим перпендикуляр ЕК на плоскость основания;
2. Из точки D опустим перпендикуляр на плоскость основания;
3. Соединим точки К и L;
4. Рассмотрим треугольник КОL. Проведенный перпендикуляр ОM
является искомым.
M
L
A
O
S
N
E
D
K
C
B
