Yamaguchi H. Engineering Fluid Mechanics (Fluid Mechanics and Its Applications)

Подождите немного. Документ загружается.

20 1 Fundamentals in Continuum Mechanics

of a material line element as displayed in Fig. 1.3, where the material line

element

xL )(t (in the material reference frame) is transformed to

)(dtt

L (in the new space frame), noting that



XLL  tdtt )( and

defining the displacement gradient tensors as

E |

෕

lim

ൺ

(1.3.3)

so that Eq. (1.3.3) can be further written as

xX | E

(1.3.4)

and

Xx |

1᧩

(1.3.5)

Eventually

E is a linear transformation tensor, and in order to verify the

principle of frame invariance we will transform a tensor

T (in the mate-

rial reference frame) to T (in the new space frame). This transformation

can be written

ETET 

(1.3.6)

and the reverse transformation is defined by

)(

11 

 ETET

(1.3.7)

Thus, the material derivative of

T in Eq. (1.3.7) will be



)()(

111111 

 ETEETEETE



(1.3.8)

denoting the material derivative, i.e.



DtD

. Equation (1.3.8) can be

further reduced to the form

TTTT

)()(

)()()()()(

111111









ETTTE

ETEETEETET





(1.3.9)

It is noted that to derive Eq. (1.3.9) we have used the relations

111 

 EEEE



and

1

 ww  EE



xuu . The relations are obtained

from Eq. (1.3.4) for the velocity

u as

 E



(1.3.10)

and

1.3 Material Objectivity and Convective Derivatives 21

1



 EEE



(1.3.11)

Consequently, the tensor (

uu ේේ  TTT



) is linearly transformed by a

material line element of

1

E , and we denote Eq. (1.3.9) as

)(

11 





 ETET



(1.3.12)

where

 is called the upper convective derivative, which is defined as fol-

lows





TTT



(1.3.13)

In the upper convective derivative, the base vectors are ‘‘contravariant’’

base vectors. That is, the base coordinate vectors are parallel to material

lines, which are deformed (stretched and rotated) with a material line.

In a similar manner, with ‘‘covariant’’ base vectors, that are normal to

material planes, where in a deformation each base vector rotates to remain

normal and stretches so that its length remains proportional to the area of

the material plane to which it is normal, we have the lower convective de-

rivative defined by

uu  TTTT



(1.3.14)

If we extend further, we will see that when material lines are in a de-

formation with rotational coordinates, we can define the derivative in the

following manner

ȦTTȦTT 



(1.3.15a)

or alternatively



ȦTTȦTT 



(1.3.15b)

where

Ȧ is the spin tensor and the derivative

is called the corotational

derivative (a) or the Jaumann derivative (b). The corotational (Jaumann)

derivative can be gotten from the upper convective derivative directly by

setting

ȦȦe   0ේ u , and using

ȦȦ 

22 1 Fundamentals in Continuum Mechanics

The three derivatives, Eqs. (1.3.13), (1.3.14) and (1.3.15), can satisfy

the principle of frame invariance, and this can be easily demonstrated to

meet the condition in Eq. (1.3.2) for the rotation tensor Q to give



TTTT

TTT

Q)TT

)ȍQ(QQTQ

QTQȍ)Q(Q)QT(Q









ේේ᧩᧩

᧩

(1.3.16)

So,



T meets the sufficient condition for the principle of frame invariance.

Observe that in deriving Eq. (1.3.16), the following relation was used

TTT

ȍQQQQȍ ᧩᧩  



(1.3.17)

since we have

I 

QQ , where Q is the unitary matrix, which is written

QQQQ



  ᧩ . It is further noted that the velocity gradient tensor

u itself does not satisfies the principle of frame invariance as it is shown

that

ȍQQ

QQQQ



 



(1.3.18)







XXXXxx ddds

  

112

᧩

᧩᧩

EEEE

(1.4.1)

xxxxXX dddS

TTTT



  E)(E)(E)(E

(1.4.2)

'' ' '

The displacement gradient tensor E , defined in Eqs. (1.1.13) and (1.3.3), is

not generally symmetric and contains both deformation and rotation of a

material line. Thus,

E itself is not a quantity of the frame invariance and

one may have to exclude the effect of rotation of a material line, particu-

larly when a constitutive equation is considered. In order to define finite

strain tensors, which are free from rotation, we can simply take the square

of the length of

, for the material lines before and after deforma-

tion respectively (see Fig. 1.3), such that

1.4 Displacement Gradient and Relative Strain

1.5 Reynolds’ Transport Theorem 23

Equations (1.4.1) and (1.4.2) contain metric tensors,

1᧩

)E(E

 and

E)(E 

respectively.

Hereafter we define strain tensors, one of which is called the Cauchy

strain tensor

C defined by

EEC 

(1.4.3)

and the other is called the Finger strain tensor defined by

111 

 EEC

(1.4.4)

These two tensors are both positive symmetric, and describe the deforma-

tion from

t to tt  of a material line, which are free from rotation. Con-

sidering the character of two tensors,

C and

C , we can define two

closely related relative strain tensors as follows

CIȖ

(1.4.5)

ICȖ

(1.4.6)

These two relative strain tensors are very useful and are often used in de-

riving integral constitutive equations for viscoelastic fluids.

1.5 Reynolds’ Transport Theorem

In deriving conservation equations of flow, it is particularly important to

consider the volume integral

)(

),(

dVtFI x , of which material deriva-

tive is defined as

DtDI .



tVV is a closed volume of fluid particles, or

otherwise known as a material volume (element) consisting of a represen-

tative material line, and

),( tF x is any scalar, vector, or tensor function.

Reynolds’ transport theorem concerns the rate of change of any volume in-

tegral, i.e.

DtDI .

Before proceeding further, it may be useful to consider the change of a

material volume

dV from coordinates ȟ at time

t to coordinates x at

time

t , where ȟ is the material coordinates, and they are Cartesian coor-

dinates,

),,(

321

[

ȟ . Also let the volume element

dV be

321

[

ddd ,,

of an elementary parallelepiped, as sketched in Fig. 1.7. Due to the fluid

motion, this parallelepiped

dV is moved to some neighborhood of the

Cartesian point

),( tȟxx

at time t , with the volume element of dV,



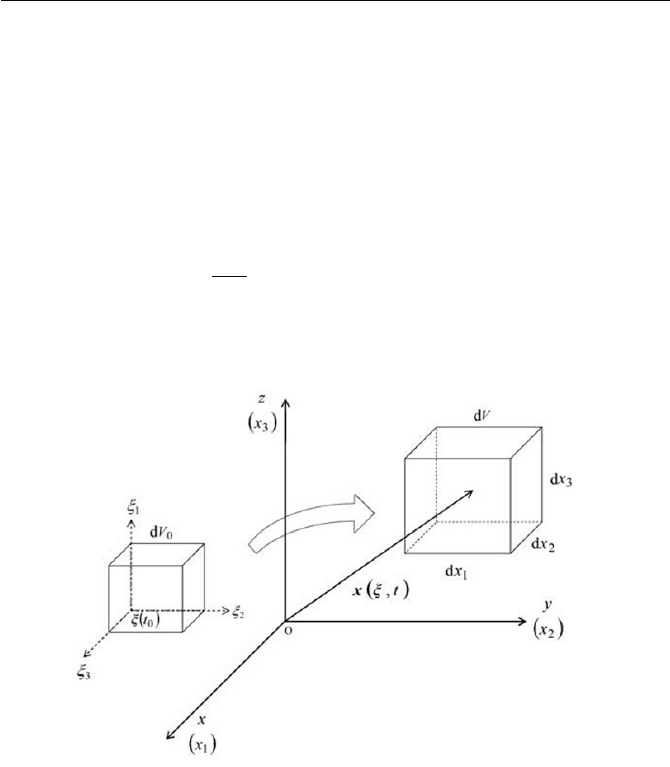
24 1 Fundamentals in Continuum Mechanics

whose sides are

dx ,

dx and

dx , i.e.

321

dxdxdxdV . The change of co-

ordinates

),,(

321

xxx x must be given to the corresponding coordinates

),,(

321

[

ȟ by

),,(

321

[

(1.5.1)

The sides

dx ,

dx and

dx of the volume element can be given by chain

rule as

dȟ

෕

for 3,2,1 i

(1.5.2)

Fig. 1.7 Change of material volume at time

The resultant volume element dV can be calculated by the box product

of vectors’

xd ,

xd , and

xd three sides, representing material line

elements of





321

321321

[[[

ddJd

dddddddV

u xxxxxx

(1.5.3)

where

is called the Jacobian of the transformation of the variables, and

is defined as

1.5 Reynolds’ Transport Theorem 25



321

෕

[[[

xxx

ȟȟȟ

xxx

kji

ijk

(1.5.4)

From the relation given by Eq. (1.5.3),

is the ratio of a material vol-

ume element to its initial volume as

(1.5.5)

and

VJdVd . This is called the dilatation.

In consideration of the dilatation, the time derivative (the material de-

rivative) of the volume integral



)(

dVtFI x can be written (by

means of the Lagrangian description)

 

෾

෾෾

VV(t)

dVJttF

dVtF



,,, ȟxx

(1.5.6)

Using the definition of the divergence in Eq. (1.1.22), we can obtain

the dilatation’s relative rate of change along a path line of a fluid particle

as follows

 

JtD

JdVD

JdVDt

dVD

div

111

(1.5.7)

Thus, from Eqs. (1.5.6) and (1.5.7) we can obtain the following relation-

ship

 

dVF

JdVF









uu ේේ

෾෾

(1.5.8)

The formula (1.5.8) is called the Reynolds’ transport theorem, and can be

further extended into a number of different forms, using the definition of

the material derivative given by Eq. (1.1.7) as

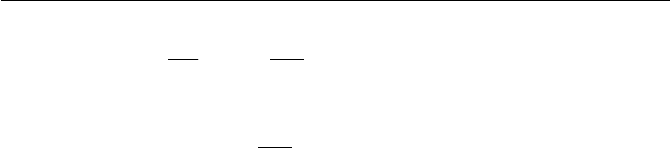
26 1 Fundamentals in Continuum Mechanics



dVF





uේ

෕

෾

(1.5.9)

dSFdV

un 

෕

෾෾

(1.5.10)

It should be noted that the Gauss’ divergence theorem was applied in order

to write the surface integral

dS~ from the volume integral

dV~ .

The physical picture of the Reynolds’ transport theorem is that the rate

of change of the integral of

in Lagrangian description is the sum of the

integral of the rate of change at a point, and the net flow of

over the

control volume surface in Eulerian description.

1.6 Forces on Volume Element

There are two kinds of forces acting on a volume element of a continuum

medium. The volume element taken in a flow field is called the control

volume in Eulerian description and equivalently called the fluid particle in

Lagrangian description. In both cases, as depicted in Fig. 1.8, “Body

forces” as one of the two kinds, can be regarded as reaching the medium

and acting over the entire volume. Body forces, which are represented by a

symbol

g, are due to long-range forces, such as gravitation (with the

gravitational acceleration

g) or electromagnetic forces, etc. They are usu-

ally independent from a deformation of the volume element and are caused

by an external field of source.

“Surface forces”, of another kind, are to be regarded as acting upon the

surface of each part of the volume element. The origins of surface forces

are chiefly due to two short-range forces, viscous and elastic forces, those

have strong dependence on a deformation of the volume element. The sur-

face forces have molecular origin in the vicinity of the surface, and act on

internal forces through the surface. Surface forces may also be generated

by an externally applied field, such as electromagnetic field, through sur-

face coupling. We shall see detailed descriptions of body forces and sur-

face forces in later chapters, such as Chapter 7 and Chapter 8. However, at

present we will treat the surface forces, with reference to stresses, that can

be represented by a stress tensor. We follow to define a general stress ten-

sor in a continuum medium, in this chapter, through Cauchy’s fundamental

theorem for stress.

1.6 Forces on Volume Element 27

Stress is a vector quantity defined as a force per unit area. Let

be a

force exerted across an area

, on which the unit outward normal vector

is acting by the material. From Cauchy’s theorem, the stress vector at

the point

a of S located by a position vector

at time t can be defined



,lim

(1.6.1)

Fig. 1.8 Body and surface forces

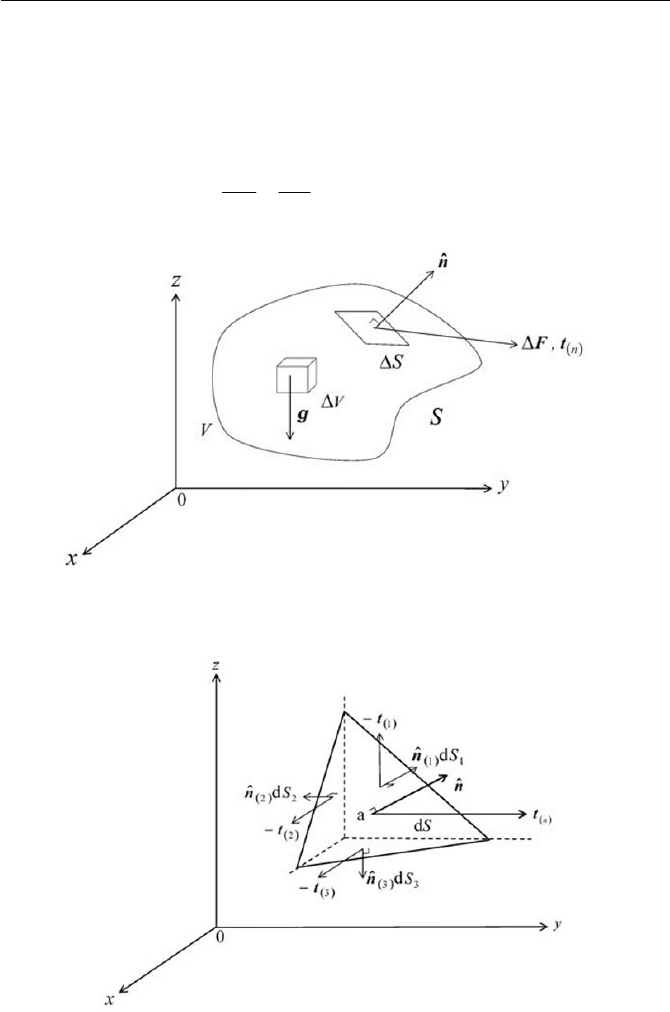
Fig. 1.9 Stresses on surface elements

28 1 Fundamentals in Continuum Mechanics

In order to give an insight to the nature of the stress



t at point a, we

consider an elementary tetrahedron of the body as schematically displayed

in Fig. 1.9, where the front surface

dS has a normal unit vector of n

. As

elucidated in Fig. 1.9, the small tetrahedron has three of its faces, where

the surface elements are



111

dSd nS



222

dSd nS

and



333

dSd nS

denoting



the normal unit vector and

dS the area of each element. We

may further indicate the stress vectors over each of three faces, by



t for 1,

2, 3 and

n. Since the surface of the tetrahedron is closed, owing that four

faces

1 i , 2, 3 and n bind the tetrahedron, we apply the principle of local

equilibrium to the stress forces, subjecting to infinitesimal tetrahedron, so

that

   



332211

 dSdSdSdS

tttt

(1.6.2)

Then, in the limit of 0

dS , we can write the components of the surface

element in such a way that

   





   





dSdSdSdS

321332211

ˆˆ

nnnnnn

(1.6.3)

since

321

dSdSdSdS can certainly be true. Thus Eq. (1.6.2)

becomes

          



332211

tntntnnt

ˆˆˆˆ



(1.6.4)

The expression in the parenthesis is a dyadic and each term in the paren-

thesis has three components, that is

  

jjj

eetneetneetn

ˆˆˆ

332

221

(1.6.5)

where

 

shows the vector components of



on the surface of

 

dSn

facing



direction, and so on.

Using the dyadic notation, Eq. (1.6.5) can be written as

jiij

TTT

ˆˆ

333231

232221

131211

(1.6.6)

1.6 Forces on Volume Element 29

where T is called the stress tensor, which has components of a second or-

der matrix. Therefore, Eq. (1.6.4) can be written alternatively with the

stress

T by

ijij

Tnt

(1.6.7)



 nt

(1.6.8)

The expression of Eq. (1.6.6) is called Cauchy’s stress formula. It can

be verified by some tensor calculus that

 

, where

T is the

transpose of

T . It is, however, only true that when the tensor T is sym-

metric, the relationship of

 

can be held.

The diagonal components

T ,

T and

T of the stress tensor T are

called the normal stresses and the off-diagonal components

T ,

T and

T are called the shear stresses.

When continuum medium is at rest, implying that fluid velocity is

identically zero at any given time, any stress acting upon a volume element

is called hydrostatic stress, except for very specific cases in non-

Newtonian fluids or electromagnetic medium, which will be introduced in

the later chapters. The hydrostatic stress is a normal stress, which is inde-

pendent of the orientation. The hydrostatic stress can be expressed by de-

noting

 as

jiji

pnTn 

(1.6.9)

and this expression yields the following relationship as

ijij



(1.6.10)

or alternatively

IT p

(1.6.11)

where

I is the unit tensor.

in Eqs. (1.6.10) and (1.6.11) can be identi-

fied as the thermodynamic pressure in a compressive fluid under assump-

tion that the fluid is in equilibrium even when the fluid is in motion. How-

ever, in incompressible limit,

can be treated as an independent dynamic

variable, retaining

as a pressure. Including the hydrostatic stress, the

stress tensor may be written as

ijijij



(1.6.12)