Wilkinson D.J. Stochastic Modelling for Systems Biology
Подождите немного. Документ загружается.


64
PROBABILITY MODELS
3.3
The
discrete
uniform
distribution
The theory
of
discrete random quantities covered in the previous section provides
a generic set
of
tools for studying distributions and their properties. However, there
are several important
"families"
of
discrete probability models that occur frequently
and are therefore worthy
of
special consideration. The first is the "discrete uniform
distribution," which corresponds to a generalisation
of
the number obtained by rolling
a single die. A random quantity X is discrete-uniform on the numbers from 1 to
n,
written
X~
DU(n)
if
each
of
the integers from 1 to n is equally likely to be the observed value
of
X.
We
therefore have outcome space
Sx={1,2,
...
,n}
andPMF
1-,
P(X=k)=-,
kESx.
n
The CDF at the points in
Sx
is therefore clearly given by
P(X::;k)=~,
kESx.
n
It
is straightforward to compute the expectation
of
X as
n 1
E (X) =
:E
k x
;:;:
k=l
=~tk
n
k=l
1
n(n
+ 1)
n 2
n+1
2
The variance can be calculated similarly to be
n
2
-1
Var(X)=~·
Although this distributional family seems somewhat contrived, it is especially useful
as it typically forms the starting point for the development
of
any stochastic simula-
tion algorithm.
3.4 The binomial distribution
The binomial distribution is the distribution
of
the number
of
"successes" in a series
of
n independent "trials," each
of
which results in a "success" (with probability p)
or
a "failure" (with probability 1 - p ).
If
the number
of
successes is
X,
we would write
X
rv
B(n,p)

THE GEOMETRIC DISTRIBUTION
65
~~------------------==~
Figure 3.2 PMF and CDF for a
B(B,
0.
7) distribution
to indicate that X is a binomial random quantity based on n independent trials, each
occurring with probability
p.
Let us now derive the probability mass function for X
"'
B(n,p).
Clearly X
can take on any value from 0 up to n, and no other. Therefore, we simply have to
calculate
P
(X=
k)
fork=
0, 1, 2,
...
, n. The probability
of
k successes followed
by
n
~.
k failures is clearly pk
(1
- p
)n-k.
Indeed, this is the probability
of
any
particular sequence involving k successes. There are
(~)
such sequences, so
by
the
multiplication principle, we have
p
(X=
k)
=
(~)pk(l-
p)n-k,
k = 0, 1, 2,
...
,
n.
Now, using the binomial theorem, we have
:tp
(X=
k) = t
(~)pk(1-
p)n-k
=
(p
+
[1-
p])n
=
1n
=
1,
.k=O k=O
and so this does define a valid probability distribution. There is no neat analytic
expression for the CDF
of
a binomial distribution, but
it
is straightforward to compute
and tabulate. A plot
of
the probability mass function and cumulative distribution
function
of
a particular binomial distribution is shown in Figure 3.2.
The expectation and variance
of
the binomiat distribution can be computed straight-
forwardly, and are found to be
·
E
(X)=
np
and
Var
(X)=
np(1-
p).
3.5
The
geometric distribution
The geometric distribution is the distribution
of
the number
of
independent suc-
cess/fail trials until
tlte first success is encountered.
If
X is the number
of
trials until
a success is encountered, and each independent trial has probability
p
of
being a
success, we write
X""'
Geom(p).

66
PROBABILITY MODELS
Clearly X can take on any positive
integer(Sx
= {1, 2,
...
}
),
so to deduce thePMF,
we need to calculate P
(X
= k) for k =
1,
2,
3,
....
In order to have X =
k,
we
must have an ordered sequence
of
k - 1 failures followed by one success. By the
multiplication rule, therefore,
·
P
(X=
k) =
(1-
p)k-
1
p,
k = 1,2,3,
....
For the geometric distribution, it is possible to calculate an analytic form for the
CDF
as
follows.
If
X
""
Geom(p ), then
Fx(k)
=
P(X:::;
k)
k
= 2:)1-
p)j-1p
j=1
k
= p 2.:(1
~
p)!-l
j=1
1-(1-p)k
= p X
----',,.----'-'-:-
1-(1-p)
=1-(1-p)k.
(geometric series)
Consequently, there is no need to tabulate the CDF
of
the geometric distribution.
Also note that the CDF tends to 1
as
k increases. This confirms that the PMF
we
defined does determine a valid probability distribution.
3.5.1
Useful series
in
probability
Notice that we used the sum
of
a geometric series in the derivation
of
the
CD
F.
There
are many other series that crop up in the study
of
probability. A
few
of
the more
commonly encountered series are listed below.
n 1 n
I>i-1
=
1-::._:
i=l
L
oo
i-1
1
a
=--
1-a
i=l
00
1
Liai-1
=
(1-
a)2
t=1
L
oo
·2
i-1
1
+a
z a =
-,----'7::'
.
(1-
a)3
t=1
ti=
n(n+1)
i=l
2
n 1
L i
2
=
6
n(n
+ 1)(2n + 1).
i=1
(a
>
0)
(0
<a<
1)
(0
<a<
1)
(0
<a<
1)

THE
..
?OISSON
DISTRIBUTION
67
We
will use two
of
these in the derivation.
of
the expectation and variance
of
the
geometric distribution.
3.5.2 Expectation and variance
of
geometric random quantities
Supp?se that
X"'
Geom(p). Then
Similarly,
and so
00
E(X)
=LiP
(X=
i)
i=l
00
i=l
1
= p X
(1
-
[1
- p])2
1
=-.
p
00
E
(X
2
)
= L i
2
p
(X=
i)
i=l
00
=
:L
i2(1-
p)i-lp
i=l
1 +
[1-
p]
= p X
-:-:(1-----;[!,..-1
_--"-::pj'=)3
2-p
=y,
Var (X) = E
(X
2
) -
E (X)
2
2
-p
1
y-p2
1-p
=y·
3.6
The
Poisson distribution
The Poisson distribution is a very important discrete probability distribution, which
arises in many different contexts in probability and statistics. For example,
Poisson
random quantities are often used in place
of
binomial random quantities in situations
where
n is large, p is small, and the expectation
np
is stable. The Poisson distribu-
tion is particularly important
in the context
of
stochastic modelling
of
biochemical
networks, as the number
of
reaction events occurring in a short time interval is ap-
proximately Poisson.

68
PROBABILITY
MODELS
A Poisson random variable, X with parameter
)..
is written
as
X"'
Po(>..).
3.6.1 Poisson as the limit
of
a binomial
Let
X"'
B(n,p).
Put)..=
E
(X)=
np and let n increase
andp
decrease
so
that)..
remains constant.
p
(X=
k)
=
(~)pk(1-
p)n-k,
Replacingp by
:>..jn
gives
k =
0,1,2,
..
.
,n.
P(X=k)=
(~)
(~):(1-~)n-k
n!
()..)·.k
( )..)·n-k
=
k!(n-
k)!
;;;
1
-
;;;
;>..k
n!
{1-
:>..jn)n
- k!
(n-
k)!nk
(1-
)..jn)k
;>..k
n
(n-
1)
(n-
2)
(n-
k + 1)
(1-
:>..jn)n
=
k!;;;-n--n-
· · · n
(1-
:>..jn)k
;>..k
e-A
-+-x1x1x1x···x1x-
asn-+oo
k!
1 '
)..k
-A
=
k!e
To
see the limit, note that
(1
-
:>..jn)n
-+
e->-
as
n increases (compound interest
formula).
3.6.2
PMF
If
X
"'
Po(>..),
then the PMF
of
X is
;>..k
P(X=k)=
k!e-A,
k=0,1,2,3,
....
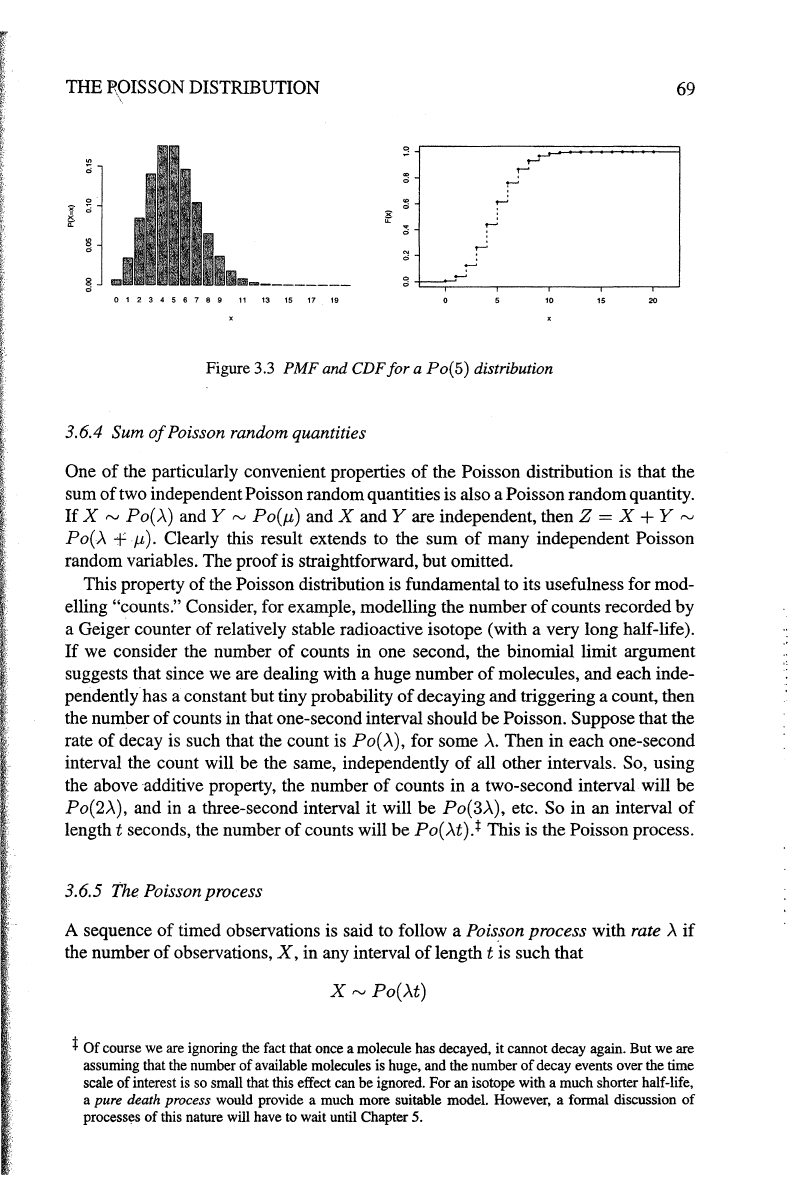
The PMF and CDF
of
X
rv
Po(5) are given in Figure 3.3.
It
is
easy to verify that
the
PMF we have adopted for X
"'
Po(.\) does indeed define a valid probability
distribution, as the probabilities sum to
1.
3.6.3 Expectation and variance
of
Poisson
If
X
rv
Po()..),
the expectation and variance can be computed directly from the PMF,
but
it
is clear from the binomial limit that we must have
E(X)
=)..
and
Var(X)
=
;>...
That is, the mean and variance are both .\.
THE
:F,OISSON
DISTRIBUTION
69
~
~
~
~
ci
~
;¥
;;
~
:;:
~
ci
0 1 2 3 4 5 6 7 8 9
11
13 15
17 19
10
15
20
Figure 3.3
PMF
and CDF for a
Po(5)
distribution
3.6.4 Sum
of
Poisson random quantities
One
of
the particularly convenient properties
of
the Poisson distribution is that the
sum
of
two independent Poisson random quantities is also a Poisson random quantity.
If
X"'
Po(
A.)
andY"'
Po(p,)
and X
andY
are independent, then Z
=X+
Y"'
Po(>..
+ p). Clearly this result extends to the sum
of
many independent Poisson
random variables. The proof is straightforward, but omitted.
This property of the Poisson distribution is fundamental to its usefulness for mod-
elling
"counts." Consider, for example, modelling the number
of
counts recorded by
a Geiger counter
of
relatively stable radioactive isotope (with a very long half-life).
If
we consider the number
of
counts in one second, the binomial limit argument
suggests that since we are dealing with a huge number
of
molecules, and each inde-
pendently has a constant but tiny probability
of
decaying and triggering a count, then
the number
of
counts in that one-second interval should be Poisson. Suppose that the
rate
of
decay is such that the count is Po(
A.),
for some>... Then in each one-second
interval the count will be the same, independently
of
all other intervals. So, using
the above additive property, the number
of
counts in a two-second interval will be
Po(2A.),
and in a three-second interval it will be
Po(3A.),
etc. So in an interval
of
length t seconds, the number
of
counts will be
Po(A.t).+
This is the Poisson process.
3.6.5 The Poisson process
A sequence
of
timed observations is said to follow a Poisson process with rate
A.
if
the number
of
observations,
X,
in any interval
of
length t is such that
X
rv
Po(A.t)
+
Of
course we are ignoring the fact that once a molecule has decayed, it cannot decay again. But we are
assuming that the number
of
available molecules is huge, and the number
of
decay events over the time
scale
of
interest is so small that this effect can be ignored. For an isotope with a much shorter half-life,
a pure death process would provide a much more suitable model. However, a formal discussion
of
processes
of
this nature will have to wait until Chapter 5.

70
PROBABILITY
MODELS
and the numbers
of
events in disjoint intervals are independent
of
one another.
We
see
that this is a simple model for discrete events occurring continuously in time. It turns
out that the
Poisson process is too simple to realistically model the time-evolution
of
biochemical networks, but a detailed understanding
of
this simple process is key
to understanding more sophisticated stochastic processes.
It
is interesting to wonder
about the time between successive events
of
the Poisson process, but it is clear that
such random times do not have a discrete distribution. This, therefore, motivates the
study
of
continuous random quantities.
3.7 Continuous probability models
3.7.1 Introduction,
PDF
and
CDF
We now turn to techniques for handling continuous random quantities. These are
random quantities with a sample space which is neither finite nor countably infinite.
The sample space is usually taken to be the real line,
or
a part thereof. Continuous
probability models are appropriate
if
the result
of
an experiment is a continuous
measurement, rather than a count
of
a discrete set. In the context
of
systems biology,
such measurements often (but not always) correspond to measurements
of
time.
If
X is a continuous random quantity with sample space S
x,
then for any particu-
lar
a E S
x,
we
generally have that
P(X
=a)=
0.
This is because the sample space is so "large" and every possible outcome so "small"
that the probability
of
any particular value is vanishingly small. Therefore, the prob-
ability mass function
we
defined for discrete random quantities is inappropriate for
understanding continuous random quantities. In order to understand continuous ran-
dom quantities, a little calculus is required.
Definition 3.13 (probability density function)
If
X is a continuous random quan-
tity, then there exists a function
f x ( x ), called the probability density function (PDF),
which satisfies the following:
1.
fx(x)
~
0,
Vx;
(the symbol "V" means ''for
all")
2.
I:
fx(x)
dx = 1;
3. P
(a
:S
X
:S
b)
=
1b
fx(x)
dx
for
any a
:S
b.
Consequently we have
1
x+8x
P(x:SX:Sx+ox)=
x
fx(y)dy
~
fx(x)ox,
f
()
P(x::;X:::;x+ox)
=}
X X
~
--~--~------~
ox
(for small ox)

CON1;'INUOUS PROBABILITY MODELS
71
and so we may interpret the PDF
as
f
( )
-
r
P(x~X~x+ox)
x x -
al~o
ox
·
Note that PDFs are not probabilities. For example, the density can take values greater
than 1 in some regions
as
long
as
it still integrates to
1.
Also note that because
P
(X=
a) =
0,
we have P
(X
s;
k) = P
(X<
k) for continuous random quan-
tities.
Definition 3.14 (cumulative distribution function) Earlier
in
this chapter
we
de-
fined the
cumulative distribution function
of
a random variable X
to
be
Fx(x)
= P
(X
s;
x),
Vx.
This definition works just as well for continuous random quantities, and is one
of
the many reasons why the distribution function is so useful.
For
a discrete random
quantity
we
had
Fx(x)
=
P(X
s;
x) =
p
(X=
y)'
{yESx!y:$x}
but for a continuous random quantity
we
have the continuous analogue
Fx(x)
= P
(X
s;
x)
= p (
-00
s;
X
s;
X)
=
[xoo
fx(z)
dz.
Just
as
in the discrete case, the distribution function is defined for all x E
JR.,
even
if
the sample space S x
is
not the whole
of
the real line.
Proposition 3.8
1.
Sinceitrepresentsaprobability,Fx(x) E
[0,1].
2.
Fx(
-oo)
= 0 and Fx(oo) =
1.
3.
lfa
<
b,
then
Fx(a)
s;
Fx(b). i.e.
Fx(·)
is a non-decreasingfunction.
4.
When X is continuous,
Fx(x)
is
continuous. Also, by the Fundamental Theorem
of
Calculus,
we
have
d
dxFx(x)
=
fx(x),
and so the slope
of
the CDF
Fx(x)
is the PDF
fx(x).
Proposition 3.9
The
median
of
a random quantity is the value m which is the "mid-
dle"
of
the distribution. That
is,
it
is
the value m such that
1
P(X
s;
m) =
2
.
Equivalently,
it
is
the
value,
m
such
that
Fx(m)
= 0.5.

72
PROBABILITY
MODELS
Similarly, the lower quartile
of
a random quantity is the value l such that
Fx
(l) = 0.25,
and the upper quartile is the value u such that
Fx(u)
= 0.75.
3.
7.2 Properties
of
continuous random quantities
Proposition 3.10 The expectation
or
mean
of
a continuous random quantity X is
given by
E(X)
=
;_:
xfx(x)dx,
which
is
just the continuous analogue
of
the corresponding formula for discrete ran-
dom quantities.
Similarly, the variance
,is
given by
Var(X)
=
;_:[x-E(XWfx(x)dx
=
;_:
x
2
fx(x)dx-
[E(X)J
2
.
Note that the expectation
of
g(X)
is
given by
E (g(X)) =
;_:
g(x)fx(x)
dx
and so the variance is just
Var (X) = E ([X - E (X)J
2
)
= E
(X
2
)
-
[E
(X)J
2
as in the discrete case.
Note that all
of
the properties
of
expectation and variance derived for discrete random
quantities also hold true in the continuous case.
It
is also worth explicitly noting the
continuous version
of
Proposition 3. 7.
Proposition 3.11
IfF
is an event and X is a continuous random quantity, then
P
(F)
=
;_:
P
(FIX=
x)
f(x)
dx
= E (P
(FIX)),
where P (FIX) is the random quantity which takes the value P (FIX =
x)
when X
takes the value x.
Proposition 3.12 (PDF
of
a linear transformation) Let X be a continuous random
quantity with
PDF
fx(x)
and CDF
Fx(x),
and let Y
=aX+
b.
The PDF
ofY
is
given by
.
~

CON1JNUOUS PROBABILITY MODELS
73
Proof.
First assume that a >
0.
It
turns out to be easier to work out the CDF first:
Fy(y)
= P
(Y:::;
y)
=
P(aX
+b:::;
y)
(
y-b)
=P
X:::;-a-
(since
a>
0)
=
Fx
(Y:
b).
So,
Fy(y)
=
Fx
(
y:
b),
and by differentiating both sides with respect to y we get
1
(y-
b)
fy(y)
=
~
fx
-a-
·
If
a <
0,
the inequality changes sign, introducing a minus sign in the expression for
the PDF. Both cases can therefore be summarised by the result.
0
Proposition 3.13 (PDF
of
a differentiable 1·1 transformation) Using a similar ar-
gument it is straightforward to deduce the
PDF
of
an arbitrary differentiable invert-
ible transformation
Y =
g(X)
as
Jy(y) =
fx
(g-l(y)) I
!g-l(y),.
Note that the term I
d~g-
1
(y)
I is known as the "Jacobian"
of
the transformation.
3.
7.3 The law
of
large numbers
In many scenarios involving stochastic simulation, it is desirable to approximate the
expectation
of
a random quantity,
X,
by the sample mean
of
a collection
of
indepen-
dent observations
of
the random quantity
X.
Suppose we have a computer program
that can simulate independent realisations
of
X (we will see in the next chapter how
to do this);
X1, Xz,
...
, Xn. The sample mean is given by
1 n
X=-
Exi.
n
i=l
If
in some appropriate sense the sample mean converges to the expectation, E
(X),
then for large
n,
we can use X as an estimate
of
E
(X).It
turns out that for random
quantities with finite variance, this is indeed true, but a couple
of
lemmas are required
before this can be made precise.
Lemma 3.6
If
X has finite mean and variance, E
(X)=
1-'
andVar
(X)=
<r
2
,
and
X1, Xz,
...
,
Xn
is a collection
of
independent realisations
of
X used to form the
