White R.E. Computational Mathematics: Models, Methods, and Analysis with MATLAB and MPI
Подождите немного. Документ загружается.

260 CHAPTER 6. HIGH PERFORMANCE COMPUTING
12.! Every processor gets values for a,b and n.
13. data a,b,n,dest,tag/0.0,100.0,1024000,0,50/
14.! Initializes mpi, gets the rank of the processor, my_rank,
15.! and number of pro cessors, p.
16. call mpi_init(ierr)
17. call mpi_comm_rank(mpi_comm_world,my_rank,ierr)
18. call mpi_comm_size(mpi_comm_world,p,ierr)
19. if (my_rank.eq.0) then
20. t1 = timef()
21. end if
22. h = (b-a)/n
23.! Each processor has unique value of loc_n, loc_a and loc_b.
24. loc_n = n/p
25. loc_a = a+my_rank*loc_n*h
26. loc_b = loc_a + loc_n*h
27.! Each processor does part of the integration.
28.! The trapezoid rule is used.
29. integral = (f(loc_a) + f(loc_b))*.5
30. x = loc_a
31. do i = 1,loc_n-1
32. x=x+h
33. integral = integral + f(x)
34. end do
35. integral = integral*h
36.! The mpi s ubroutine mpi_reduce() is used to communicate
37.! the partial integrations, integral, and then sum
38.! these to get the total numerical approximation, total.
39. call mpi_reduce(integral,total,1,mpi_real,mpi_sum,0&
40. ,mpi_comm_world,ierr)
41. call mpi_barrier(mpi_comm_world,ierr)
42. if (my_rank.eq.0) then
43. t2 = timef()
44. end if
45.! Pro cessor 0 prints the n,a,b,total
46.! and time for computation and communication.
47. if (my_rank.eq.0) then
48. print*,n
49. print*,a
50. print*,b
51. print*,total
52. print*,t2
53. end if
54.! mpi is terminated.
55. call mpi_finalize(ierr)
56. contains
© 2004 by Chapman & Hall/CRC
6.4. MPI AND THE IBM/SP 261
57.! This is the function to be integrated.
58. real function f(x)
59. implicit none
60. real x
61. f = x*x
62. end function
63. end program trapezoid
The communication command in lines 39-40 mpi_reduce() sends all the
partial integrals to processor 0, processor 0 receives them, and sums them. This
command is an e
!cient concatenation of following sequence of mpi_send() and
mpi_recv() commands:
if (my_rank .eq. 0) then
total = integral
do source = 1, p-1
call mpi_recv(integral, 1, mpi_real, source, tag,
mpi_comm_world, status, ierr)
total = total + integral
enddo
else
call mpi_send(integral, 1, mpi_real, dest,
tag, mpi_comm_world, ierr)
endif.
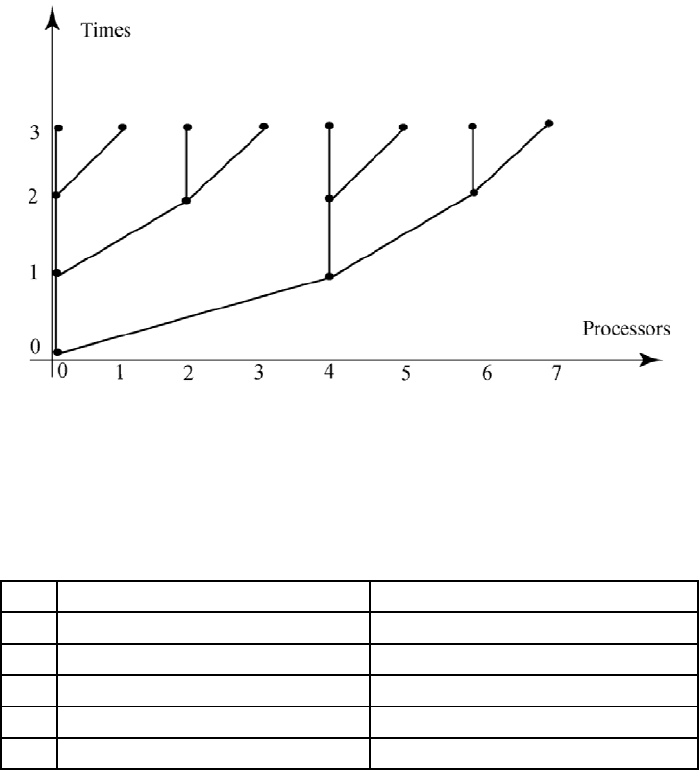
If there are a large number of processors, then the sequential source loop may
take some significant time. In the mpi_reduce() subroutine a “tree” or “fan-in”
scheme allows for the use of any available processors to do the communication.
By going
backward in time processor 0 can receive the partial integrals in 3 = log
2
(8)
time steps. Also, by going forward in time processor 0 can send information
to all the other processors in 3 times steps. In the following sections three
additional collective communication subroutines (mpi_bcast(), mpi_scatter()
will be illustrated.
The code can be compiled and executed on the IBM/SP by the following
commands:
mpxlf90 —O3 trapmpi.f
poe ./a.out —procs 2 —hfile cpus.
The mpxlf90 is a multiprocessing version of a Fortran 90 compiler. Here we
have used a third level of optimization given by —O3. The execution of the
a.out file, which was generated by the compiler, is done by the parallel operating
environment command, poe. The —procs 2 indicates the number of processors
to be used, and the —hfile cpus indicates that the processors in the file cpus are
to be used.
A better alternative is to use Load Leveler given by the llsubmit command.
In the following we simply used the command:
© 2004 by Chapman & Hall/CRC
One "tree" scheme of communication is depicted in Figure 6.4.1.
and mpi_gather())that utilize "fan-out" or "fan-in" schemes, see Figure 7.2.1,
262 CHAPTER 6. HIGH PERFORMANCE COMPUTING
Figure 6.4.1: Fan-out Communication
Table 6.4.1: MPI Times for trapempi.f
p Times(S
s
) n = 102400 Times(S
s
) n = 1024000
1 6.22(1.00) 61.59(1.00)
2 3.13(1.99) 30.87(1.99)
4 1.61(3.86) 15.48(3.98)
8 0.95(6.56) 07.89(7.81)
16 0.54(11.54) 04.24(14.54)
llsubmit envrmpi8.
This ran the compiled code with 2 nodes and 4 processors per node for a total
of 8 processors. The output will be sent to the file mpijob2.out. One can check
on the status of the job by using the command:
llq.
The code trapmpi.f generated Table 6.4.1 by using llsubmit with di
erent
numbers of CPUs or processors. The e
!ciencies (S
s
@s) decrease as the number
of processors increase. The amount of independent parallel computation in-
creases as the number of trapezoids, n, increases, and so, one expects the better
speedups in the third column than in the second column. If one decreases n
to 10240, then the speedups for 8 and 16 processors will be very poor. This
is because the communication times are very large relative to the computation
times. The execution times will vary with the choice of optimization (see man
xlf90) and with the numb er of other users (see who and llq). The reader will find
it very interesting to experiment with these parameters as well as the number
of trapezoids in trapmpi.f.
© 2004 by Chapman & Hall/CRC
6.5. MPI AND MATRIX PRODUCTS 263
6.4.4 Exercises
1. Browse the www pages for the NCSC and MPI.
2. Experiment with dierent levels of optimization in the compiler mpxlf90.
3. s and q.
4. Experiment with the alternative to mpi_reduce(), which uses a loop with
mpi_send() and mpi_recv().
5. In trapmpi.f replace the trapezoid rule with Simpson’s rule and repeat
the calculations in Table 6.4.1.
6.5 MPI and Matrix Products
6.5.1 Intro duction
In this section we will give examples of MPI/Fortran codes for matrix-vector
and matrix-matrix products. Here we will take advantage of the column order
of the arrays in Fortran. MPI communication subroutines mpi_reduce() and
mpi_gather(), and optimized BLAS (basic linear algebra subroutines) sgemv()
and sgemm() will be illustrated.
6.5.2 Matrix-vector Products
The ij method uses products of rows in the p × q matrix times the column
vector, and the ji method uses linear combinations of the columns in the
p × q
matrix. In Fortran p × q arrays are stored by columns, and so, the ji method
is best because it retrieves components of the array in stride equal to one.
Matrix-Vector Product (ji version) d
+
= d + Ax=
for m = 1> q
for l = 1> p
g
l
= g
l
+ d
l>m
{
m
endloop
endloop=
A parallel version of this algorithm will group the columns of the matrix,
that is, the j-loop will be partitioned so that the column sums are done by a
particular processor. Let eq and hq be the beginning and end of a subset of
this partition, which is to be assigned to some processor. In parallel we will
compute the following partial matrix-vector products
D(1 : p> eq : hq){(eq : hq)=
Upon completion of all the partial products, they will be communicated to some
pro cessor, usually the root processor 0, and then summed.
In the MPI/Fortran code matvecmpi.f the arrays in lines 13-15 are initialized
before MPI is initialized in lines 16-18, and therefore, each processor will have a
© 2004 by Chapman & Hall/CRC
Repeat the calculations in Table 6.4.1. Use additional
264 CHAPTER 6. HIGH PERFORMANCE COMPUTING
copy of the array. Thus, there is no need to send data via mpi_bcast() in lines
26-28; note the mpi_bcast() subroutines are commented out, and they would
only send the required data to the appropriate processors. The matrix-vector
product is done by computing a linear combination of the columns of the matrix.
The linear combination is partitioned to obtain the parallel computation. Here
these calculations are done on each processor by either the BLAS2 subroutine
in lines 30-34. Then mpi_reduce() in line 36 is used to send n real numbers
(a column vector) to processor 0, received by processor 0 and summed to the
product vector. The mflops (million floating point operations per second) are
computed in line 42 where the timings are in milliseconds and there are 1000
repetitions of the matrix-vector product.
MPI/Fortran Code matvecmpi.f
1. program matvec
2. implicit none
3. include ’mpif.h’
4. real,dimension(1:1024,1:4096):: a
5. real,dimension(1:1024)::prod,prodt
6. real,dimension(1:4096)::x
7. real:: t1,t2,mflops
8. real:: timef
9. integer:: my_rank,p,n,source,dest,tag,ierr,loc_m
10. integer:: i,status(mpi_status_size),bn,en,j,it,m
11. data n,dest,tag/1024,0,50/
12. m = 4*n
13. a = 1.0
14. prod = 0.0
15. x = 3.0
16. call mpi_init(ierr)
17. call mpi_comm_rank(mpi_comm_world,my_rank,ierr)
18. call mpi_comm_size(mpi_comm_world,p,ierr)
19. loc_m = m/p
20. bn = 1+(my_rank)*loc_m
21. en = bn + loc_m - 1
22. if (my_rank.eq.0) then
23. t1 = timef()
24. end if
25. do it = 1,1000
26. ! call mpi_bcast(a(1,bn),n*(en-bn+1),mpi_real,0,
mpi_comm_world,ierr)
27. ! call mpi_bcast(prod(1),n,mpi_real,0,
mpi_comm_world,ierr)
28. ! call mpi_bcast(x(bn),(en-bn+1),mpi_real,0,
mpi_comm_world,ierr)
© 2004 by Chapman & Hall/CRC
sgemv() (see http://www.netlib.org /blas/sgem v.f ) in line 29, or by the ji-loops

6.5. MPI AND MATRIX PRODUCTS 265
Table 6.5.1: Matrix-vector Product mflops
p sgemv, m = 2048 sgemv, m = 4096 ji-loops, m = 4096
1 430 395 328
2 890 843 683
4 1628 1668 1391
8 2421 2803 2522
16 3288 4508 3946
29. ! call sgemv(’N’,n,loc_m,1.0,a(1,bn),n,x(bn),1,1.0,prod,1)
30. do j = bn,en
31. do i = 1,n
32. prod(i) = prod(i) + a(i,j)*x(j)
33. end do
34. end do
35. call mpi_barrier(mpi_comm_world,ierr)
36. call mpi_reduce(prod(1),pro dt(1),n,mpi_real,mpi_sum,0,
mpi_comm_world,ierr)
37. end do
38. if (my_rank.eq.0) then
39. t2 = timef()
40. end if
41. if (my_rank.eq.0) then
42. mflops =float(2*n*m)*1./t2
43. print*,prodt(n/3)
44. print*,prodt(n/2)
45. print*,prodt(n/4)
46. print*,t2,mflops
47. end if
48. call mpi_finalize(ierr)
49. end program
Table 6.5.1 records the mflops for 1000 repetitions of a matrix-vector product
where the matrix is
q × p with q = 1048 and variable p. Columns two and
three use the BLAS2 subroutine sgemv() with
p = 2048 and 4096. The mflops
are greater for larger
p. The fourth column uses the ji-loops in place of the
optimized sgemv(), and smaller mflops are recorded.
6.5.3 Matrix-matrix Products
Matrix-matrix products have three nested loops, and therefore, there are six
possible ways to compute these products. Let
D be the product E times F.
The traditional order is the ijk method or dotproduct method, which computes
row
l times column m. The jki method computes column m of D by multiplying
© 2004 by Chapman & Hall/CRC
266 CHAPTER 6. HIGH PERFORMANCE COMPUTING
E times column m of C, which is done by linear combinations of the columns of
E. D is initialized to zero.
Matrix-matrix Product (jki version) A
+
= A + BC=
for m = 1> q
for n = 1> q
for l = 1> p
d
l>m
= d
l>m
+ e
l>n
f
n>m
endloop
endloop
endloop.
This is used in the following MPI/Fortran implementation of the matrix-
matrix product. Here the outer j-loop can be partitioned and the smaller
matrix-matrix products can be done concurrently. Let eq and hq be the begin-
ing and end of a subset of the partition. Then the following smaller matrix-
matrix products can be done in parallel
E(1 : p> 1 : q)F(1 : q> eq : hq)=
Then the smaller products are gathered into the larger product matrix. The
center k-loop can also be partitioned, and this could be done by any vector
pipelines or by the CPUs within a node.
The arrays are initialized in lines 12-13 before MPI is initialized in lines
15-17, and therefore, each processor will have a copy of the array. The matrix-
matrix products on the submatrices can be done by either a call to the optimized
26, or by the jki-loops in lines 27-33. The mpi_gather() subroutine is used
in line 34, and here
qp real numbers are sent to processor 0, received by
processor 0 and stored in the product matrix. The mflops (million floating
point operations per second) are computed in line 41 where we have used the
timings in milliseconds, and ten repetitions of the matrix-matrix product with
qp dotproducts of vectors with q components.
MPI/Fortran Code mmmpi.f
1. program mm
2. implicit none
3. include ’mpif.h’
4. real,dimension(1:1024,1:512):: a,b,prodt
5. real,dimension(1:512,1:512):: c
6. real:: t1,t2
7. real:: timef,mflops
8. integer:: l, my_rank,p,n,source,dest,tag,ierr,loc_n
9. integer:: i,status(mpi_status_size),bn,en,j,k,it,m
10. data n,dest,tag/512,0,50/
11. m = 2*n
© 2004 by Chapman & Hall/CRC
BLAS3 subroutine sgemm() (see http://www.netlib.org /blas/sgemm.f) in line
6.5. MPI AND MATRIX PRODUCTS 267
12. a = 0.0
13. b = 2.0
14. c = 3.0
15. call mpi_init(ierr)
16. call mpi_comm_rank(mpi_comm_world,my_rank,ierr)
17. call mpi_comm_size(mpi_comm_world,p,ierr)
18. loc_n = n/p
19. bn = 1+(my_rank)*loc_n
20. en = bn + loc_n - 1
21. call mpi_barrier(mpi_comm_world,ierr)
22. if (my_rank.eq.0) then
23. t1 = timef()
24. end if
25. do it = 1,10
26. call sgemm(’N’,’N’,m,loc_n,n,1.0,b(1,1),m,c(1,bn) &
,n,1.0,a(1,bn),m)
27. ! do j = bn,en
28. ! do k = 1,n
29. ! do i = 1,m
30. ! a(i,j) = a(i,j) + b(i,k)*c(k,j)
31. ! end do
32. ! end do
33. ! end do
34. call mpi_barrier(mpi_comm_world,ierr)
35. call mpi_gather(a(1,bn),m*loc_n,mpi_real,prodt, &
m*loc_n, mpi_real,0,mpi_comm_world,ierr)
36. end do
37. if (my_rank.eq.0) then
38. t2= timef()
39. end if
40. if (my_rank.eq.0) then
41. mflops = 2*n*n*m*0.01/t2
42. print*,t2,mflops
43. end if
44. call mpi_finalize(ierr)
45. end program
D with p = 2q rows and q columns.
The second and third columns use the jki-loops with
q = 256 and 512, and the
speedup is generally better for the larger
q. Column four uses the sgemm to
do the matrix-matrix products, and noticeable improvement in the mflops is
recorded.
© 2004 by Chapman & Hall/CRC
In Table 6.5.2 the calculations were for

268 CHAPTER 6. HIGH PERFORMANCE COMPUTING
Table 6.5.2: Matrix-matrix Product mflops
p jki-loops, n = 256 jki-loops, n = 512 sgemm, n = 512
1 384 381 1337
2 754 757 2521
4 1419 1474 4375
8 2403 2785 7572
16 4102 5038 10429
6.5.4 Exercise
1. Browse the www for MPI sites.
2. In matvecmpi.f experiment with di
erent n and compare mflops.
3. In matvecmpi.f experiment with the ij-loop metho d and compare mflops.
4. In matvecmpi.f use sgemv() to compute the matrix-vector product. You
may need to use a special compiler option for sgemv(), for example, on the
IBM/SP use -lessl to gain access to the engineering and scientific subroutine
library.
5. In mmmpi.f experiment with di
erent n and compare mflops.
6. In mmmpi.f experiment with other variations of the jki-loop method and
compare mflops.
7. In mmmpi.f use sgemm() and to compute the matrix-matrix product.
You may need to use a special compiler option for sgemm(), for example, on
the IBM/SP use -lessl to gain access to the engineering and scientific subroutine
library.
6.6 MPI and 2D Models
6.6.1 Introduction
In this section we will give examples of MPI/Fortran codes for heat diusion
and pollutant transfer in two directions. Both the discrete models generate 2D
arrays for the temperature, or pollutant concentration, as a function of discrete
space for each time step. These models could b e viewed as a special case of the
matrix-vector products where the matrix is sparse and the column vectors are
represented as a 2D space grid array.
6.6.2 Heat Diusion in Two Directions
The basic model for heat diusion in two directions was formulated in Section
1.5.
© 2004 by Chapman & Hall/CRC
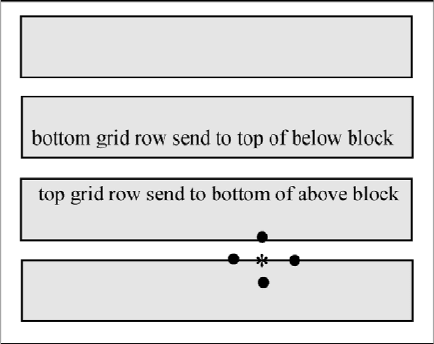
6.6. MPI AND 2D MODELS 269
Figure 6.6.1: Space Grid with Four Subblocks
Explicit Finite Di
erence 2D Model: u
n
l>m
x(lk> mk> nw)=
x
n+1
l>m
= (w@f)i + (x
n
l
+1>m
+ x
n
l
1>m
+ x
n
l>m
+1
+ x
n
l>m
1
)
+(1
4)x
n
l>m
> (6.6.1)
= (N@f)(w@k
2
)> l> m = 1> ==> q 1 and n = 0> ==> pd{n 1>
x
0
l>m
= given> l> m = 1> ==> q 1 and (6.6.2)
x
n
l>m
= given> n = 1> ===> pd{n, and l> m on the boundary grid. (6.6.3)
The execution of (6.6.1) requires at least a 2D array u(i,j) and three nested
loops where the time loop (k-loop) must be on the outside. The two inner loops
are over the space grid for x (i-loop) and y (j-loop). In order to distribute the
work, we will partition the space grid into horizontal blocks by partitioning
the j-loop. Then each pro cessor will do the computations in (6.6.1) for some
partition of the j-loop and all the i-loop, that is, over some horizontal block of
the space grid. Because the calculations for each ij (depicted in Figure 6.6.1 by
*) require inputs from the four adjacent space nodes (depicted in Figure 6.6.1
by •), some communication must be done so that the bottom and top rows of
the partitioned space can be computed. See Figure 6.6.1 where there are four
horizontal subblocks in the space grid, and three pairs of grid rows must be
communicated.
The communication at each time step is done by a sequence of mpi_send()
and mpi_recv() subroutines. Here one must be careful to avoid "deadlocked"
communications, which can occur if two processors try to send data to each
other at the same time. One needs mpi_send() and mpi_recv() to be coupled
with respect to time.
cations for eight processors associated with eight horizontal subblo cks in the
space grid. Each vector indicates a pair of mpi_send() and mpi_recv() where
the processor at the beginning of the vector is sending data and the processor
© 2004 by Chapman & Hall/CRC
Figure 6.6.2 depicts one way of pairing the communi-
