Water Power and Dam Construction

Подождите немного. Документ загружается.

WWW.WATERPOWERMAGAZINE.COM OCTOBER 2009 31

WAVE & TIDAL POWER

COTLAND has the potential to be a powerhouse of marine

energy. Although this is the ﬁrmly held belief of those work-

ing to develop such technology within the region, the facts

do speak for themselves.

Scottish seas account for 25% of Europe’s tidal stream resource

and 10% of Europe’s wave resource. And Scottish government

estimates suggest that 21.5GW of wave and tidal energy could

be generated from Scottish waters – providing almost 50% of the

country’s energy demands. Furthermore, the marine energy indus-

try has the potential to provide up to 12,500 jobs, contributing up

to £2.5B (US$4B) to the Scottish economy by 2020.

Scottish company Aquamarine Power is one of the key players in

the wave and tidal power industry, having developed Oyster – the

UK’s ﬁrst nearshore wave energy converter. The company’s chief

executive, Martin McAdam, spoke about the importance of secur-

ing the future development of this industry.

“We have a vast resource, and the vital engineering and manu-

facturing skills,” he said. “As a nation we have the necessary drive

and determination to lead this brand new industry. At this early

stage of development, the marine energy industry needs consistent

support to help reach its full potential. It’s not just funding and

investment that is required; it’s the solutions that help to save our

most precious commodity: time.”

Although it is recognised that Scotland has the potential for the

healthy development of marine energy technology, these technolo-

gies have very different development paths compared with other

‘wet renewables’, such as tidal impoundment, marine biomass and

offshore wind. Scotland’s marine energy industry has made signiﬁ-

cant steps forward over the past ﬁve years, but the technology has

not developed as quickly as analysts had predicted.

The story, however, may read differently over the next ﬁve years.

The wheels of change are in motion and the industry may soon be

accelerating down the road to progress. The Scottish government

recognises that this is a key growth area, both in terms of increasing

the rate of economic growth and in addressing the pressing needs of

climate change. Over the past six months the engines of the Scottish

powerhouse have been ﬁnely tuned to help deliver a new future for

the country’s seas.

MARIN E SCOTLAND

The ﬁrst step has been the establishment of an integrated marine

management organisation. Marine Scotland is a directorate of the

Scottish government, bringing together the functions and resourc-

es of the former Marine Directorate, Fisheries Research Services

and the Scottish Fisheries Protection Agency. As McAdam said:

“Marine Scotland will be a one-stop shop for developers to get our

wave and tidal power devices from the drawing board and into the

water for testing as quickly and efﬁciently as possible.”

Then on 29 April 2009, the Scottish government introduced its

ﬁrst Marine Bill. Its aims are to balance the protection of the marine

environment while supporting the sustainable economic develop-

Above: The 194-tonne full scale nearshore wave energy converter, Oyster, was

bolted onto its seabed subframe in August 2009. The device has been deployed

at the European Marine Energy Centre in Orkney, Scotland. Aquamarine Power,

Oyster’s developer, has signed an agreement with Airtricity for the creation of

up to 1000MW of marine energy sites by 2020 using Oyster technology.

Scotland has the potential to build a world-

leading marine energy industry. Although

signiﬁcant advances have been made over

recent years, development has been slower

than expected. The introduction of new

legislation and government bodies, plus

the publication of an industry-led report,

looks set to accelerate the pace of change.

Suzanne Pritchard gives an insight into

Scotland’s marine energy prowess, assessing

the current status of the industry and

explaining the importance of the Marine

Energy Road Map

Mapping out a

powerful future

for Scotland

32 OCTOBER 2009 INTERNATIONAL WATER POWER & DAM CONSTRUCTION

WAVE & TIDAL POWER

ment of marine industries; ultimately providing a coherent frame-

work and stable environment to promote investment in renewable

projects. Marine Scotland, through the Scottish Marine Bill, will

make planning and consenting a more streamlined process.

“Compared to the rest of the UK, in Scotland the waters tend

to be more oceanic and deeper, the coastline is less heavily popu-

lated and ﬁshing and aquaculture are a much larger part of the

marine picture. However, as in the rest of the UK, competition for

marine space and resources can be intense. The need to manage

such competition is at the heart of the Scottish Bill,” John Booth,

spokesperson for the Scottish government, explained.

The Bill introduces a framework to deliver sustainable economic

growth by improving stewardship of Scotland’s seas, including:

U Marine planning – a statutory planning system will manage the

increasing and often conﬂicting demands on the seas.

U Marine licensing – a simpler licensing system will minimise the

number of licences required for development in the marine envi-

ronment to cut bureaucracy and encourage economic investment.

In addition, provisions in the Bill allow Section 36 consents for

renewable generation to be considered alongside a new licence

for construction and navigation issues.

National marine plans will also set out the objectives and broad tar-

gets for the marine renewables industry at a Scottish level. Marine

plans at the regional level will add a greater spatial dimension to

the national plans identifying areas that could be appropriate for

a variety of activities. This enhanced level of spatial information

will provide developers with more information on possible sites

reducing search costs and hopefully reducing timescales.

POWER FU L ROAD MAP

The latest development was the publication of the Marine Energy

Road Map in August 2009. The report was produced by the

Marine Energy Group (MEG). This is an industry-led collabo-

ration under the auspices of the Forum for Renewable Energy

Development in Scotland (FREDS).

The vision of FREDS Marine Energy Group is to create a world-

leading marine energy industry. In order to achieve this, the group

has recognised a distinction between two needs:

U Promoting market opportunities for marine energy generation.

U Ensuring that Scottish companies and communities are well

placed to capture these opportunities.

The group’s road map gives an up-to-date assessment of the status

and potential of the marine energy industry in Scotland. Ultimately,

its aims are to chart a course for wave and tidal power around

Scotland, recommending actions to ensure Scotland takes full

advantage of the vast power of the seas. The recommendations are

industry driven and will be presented to Scottish and UK govern-

ment ministers, public bodies, regulatory and enterprise agencies,

and the private sector. At the heart of this work is the agreement

that the government, its partners and industry will continue to

work together to build a world leading renewables sector.

The road map makes various recommendations, the most impor-

tant of which is the urgent need for ﬁnancial support. Since 2004

the industry has achieved some signiﬁcant milestones. Investment-

wise the sector now attracts blue-chip and institutional investors

who are viewing Scotland as a preferred investment location due to

its high support tariff, strength of commitment to the sector, and

consistency of support from the government, local communities

and industry. Utilities are closely involved with pre-commercial

projects indicating conﬁdence and a belief that the basic building

blocks for growth are largely in place, while national grid and

transmission operators are also giving assurance about the recog-

nised need for new grid connections, in time for proposed technol-

ogy deployments in the islands and coastal areas of Scotland. In

addition, conﬁdence that the investments meet wider economic

performance standards has been demonstrated through the market

listing of leading marine technology developers.

However, MEG states that given its emerging nature the indus-

try still faces relatively high costs and perceptions of high risk.

Ultimately this means that it is more difﬁcult to attract private

ﬁnance here than in other renewable sectors, particularly for proto-

type and pre-commercial developments. And now such difﬁculties

are taking place within the context of a global recession. Indeed,

the pace of advancement has been slower than previously esti-

mated, due to underestimating technical challenges and difﬁculty

securing sufﬁcient ﬁnancial support. But the marine energy indus-

try now needs the devices to develop from the prototype stage.

MEG recognises that insufﬁcient or misdirected ﬁnancial sup-

port is a key barrier to the pace of success. Current funding for the

different technology stages includes The Carbon Trust Applied

Research Fund, the Energy Technologies Institute, the Scottish

government’s Wave and Tidal Energy Support Scheme (WATES)

and the banded renewables obligation.

However MEG recommends that there is now a need to create

a market pull and reduce ﬁnancial risk for marine energy. As cap-

ital risk peaks at stages two and three of project development,

MEG recommends that up-front capital risks are diluted in order

to attract the private sector commitment needed to deliver these

schemes. The Marine Energy Road Map emphasises that contin-

ued investment is vital and lists various funding recommendations

throughout the stages in order to ensure a consistent innovation

pipeline. These include:

Stage one:

U Get the Scottish government to consider the roles of various

public bodies to ensure that they are supporting marine energy

projects.

U Encourage funding councils to award more to marine energy.

U Ask the European Commission to include marine energy within

future work plans under its seventh framework programme.

Stage two

U Introduce a ﬂexible WATES-style initiative as an open call with

an annual allocation.

U Get the government treasury to include marine energy technology

in the Energy Technology Criteria List to enable devices at stages

2 and 3 to attract a capital write down allowance of 100%,

opposed to the current 10%. Plus release funding for renewables,

including marine technology, from the Fossil Fuel Levy.

Marine Energy Group - members

U Aquamarine Power. U Aquatera

U AWS Ocean Energy. U European Marine Energy Centre.

U National Grid. U Pelamis Wave Power.

U Scottish Power Renewables. U Scottish & Southern Energy.

U Scottish Enterprise. U Subsea UK.

U University of Edinburgh. U Wavegen.

U Representatives from the Scottish government.

U Scottish Development International.

Funding context

Technology development stages Typical project budgets

Stage 1: Proof of concept and pre-prototype £500K to £5M (US$824K-8M)

scale testing at sea

Stage 2: Full scale prototype £10M (US$16M)

Stage 3: Demonstration project/array £10-50M (US$16-82M)

Stage 4: Commercial project £20M+ (US$33M)

WWW.WATERPOWERMAGAZINE.COM OCTOBER 2009 33

WAVE & TIDAL POWER

Stage three:

U Get the government to introduce a WATES-style stage 3 support

in recognition of increased capital costs at this stage.

Stage four:

U The government should review the level of renewable obligation

banding for tidal stream in line with the band for wave energy.

There is no strong evidence to support a banding differentiation

between the two technologies.

OVERC OM ING BARR IE RS TO DEV ELOPMENT

In its road map the Marine Energy Group identiﬁ ed other areas

needing further development. For example, grid capacity is very

limited in the north and northwest of Scotland where much of

the marine energy potential is located. Additional upgrades will

be necessary for future development. Through its grid sub group

MEG will identify long term grid infrastructure upgrades on the

basis of expected development locations. It also urges Scottish

Ministers to give the go ahead for the Beauly-Denny link as it will

not only provide capacity for renewable projects most ready for

connection, but it is also the key to unlocking further progress

on network upgrades. Scottish Hydroelectric Transmission is also

encouraged to build two new transmission routes.

Other recommendations pinpointed by MEG include a focus

on infrastructure. The Scottish government is currently undertak-

ing a National Renewables Infrastructure Project which is set to

report in late 2009 on the current facilities available and future

opportunities for expansion. MEG wants to feed into the spatial

framework being drawn up and give information on infrastructure

requirements for marine renewables.

Closer links with Europe are also required. MEG recommends that

the Scottish industry works with the European Commission to raise

the proﬁ le of marine renewables within Europe. It believes that the EC

does not yet perceive marine renewables to be commercially viable,

and as a result they are not featured in the European Strategic Energy

Technology Plan. Therefore, amongst other actions, MEG wants to

present its road map to the EC and a wider European audience to

promote more effective support for the technology.

LARGE -SCALE DEP LO YMENT

The Marine Energy Road Map acknowledges that the large-scale

deployment of marine technology in Scottish water is possible by

2020, but it requires fast and concerted action by all players, cou-

pled with a strong leadership role for the public sector. In order to

assess progress, MEG will review the report’s recommendations in

the summer of 2012.

“The road map shows that Scotland has the potential to build

a world-leading marine energy industry,” said McAdam from

Aquamarine Power. “Scotland had a global lead in marine renew-

able technology but the next step, building and developing com-

mercial wave and tidal farms to prove long term viability of the

technology, will cost each developer between £30-50M. Much of

this is being raised from the private sector, but at this early stage

of the industry, government support is essential.

“If the Scottish government continues to support us, together

with the UK parliament and Europe, we can build an industry to

make Scotland proud.”

Marine energy denotes both wave and tidal stream

technologies, as deﬁ ned in the Marine Energy Group’s

Marine Energy Road Map

Watertight doors & hatches

for when it really matters.

Any pressure; any location.

Walz & Krenzer, Inc.

Tel: 203.267.5712 | sales@wkdoors.com

www.ﬂoodbarriers.com | www.wkdoors.com

t*NQFSNFBCMF

t'MFYJCMF

t3FTJTUBOUUPTFUUMFNFOUT

t*OTUBMMFERVJDLMZ

BMTPVOEFSXBUFS

t%VSBCMF

t"QQMJDBCMFUPBMMUZQFT

PGTUSVDUVSFT

t&OWJSPONFOUBMMZGSJFOEMZ

t&GGJDJFOUMZNPOJUPSFE

(&0.&.#3"/&4"3&

#JH5PPUI64"&YQPTFE17$HFPNFNCSBOFUPXBUFSQSPPGB

NIJHISPDLGJMMEBN+VMZ8BUFSTVQQMZ

$"31*4:/5)&5*$(&0.&.#3"/&4

)"7&45011&%-&","(&*/%".4

4JODF

1,200+ projects completed. Design and supply of waterproofing systems for

dams, canals, hydraulic tunnels, reservoirs. Dry and underwater installation.

$"31*5&$)

$PSTP4BO(PUUBSEP$IJBTTP4XJU[FSMBOE

1I 'BY

XXXDBSQJUFDIDPN FNBJMJOGP!DBSQJUFDIDPN

Carpi_Sept 09:Carpi ad Oct07 10/9/09 08:42 Page 1

IWP& DC

34 OCTOBER 2009 INTERNATIONAL WATER POWER & DAM CONSTRUCTION

A methodology for the determination of generator inertia for isolated impulse turbined

hydro systems is developed based on an analysis of 25 units having installed capacities

varying from about 1MW to over 60MW

Hydro impulse turbine speed regulation

HE methodology outlined in a previous paper (1) on this

subject, covering reaction units, was used to determine

whether the same procedure is applicable to impulse

units. It was found that isolated impulse units could oper-

ate effectively with a fraction of the minimum inertia previously

suggested. This is primarily due to the dual mode of ﬂow control,

by needle valve, and by a deﬂector on the jet which rapidly cuts

off ﬂow when the speed rises above synchronous. This is clearly

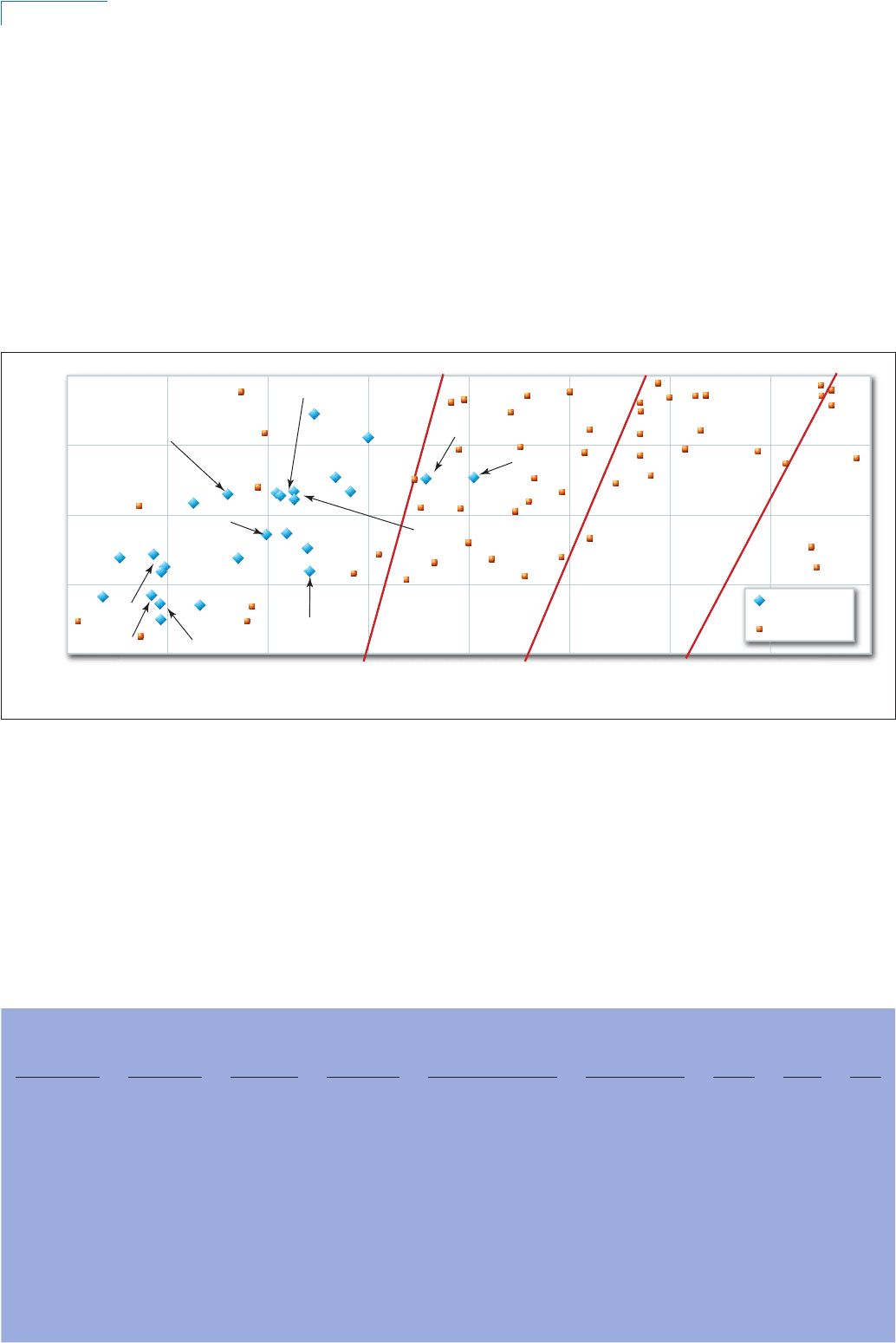
illustrated in Figure 1, where the plant characteristics are plotted

on the chart applicable to reaction units, and most impulse units

fall into Area A, designated for units which cannot provide any

form of frequency control. Frequency control, derived from reac-

tion unit data, can only commence when unit characteristics have

a T

ratio in excess of about 1.0.

Based on this analysis, it was decided to determine whether an

improved methodology could be developed for impulse units which

could more precisely deﬁne their ability to control frequency. Finding

isolated impulse turbine powered utility systems is difﬁcult, and there

are very few examples to study. However, lessons can be learned

from early experience with three isolated systems in Bolivia, provid-

ing electricity to the cities of La Paz, Oruro, and Cochabamba. The

principal characteristics of units associated with these systems are

shown in Table 1, along with one Canadian development at Cat Arm

in Newfoundland.

TURBINES

0.4

0.3

0.2

0.1

0.0

Waterhammer ratio = Tw/Te

0.0 0.2 0.4 0.6

Unit start/total governor open time = Tm/Tg

0.8 1.0 1.2 1.4 1.6

Impulse units

Reaction units

Santa Rosa #2

Santa Rosa #1

Angostura

Achachicala

Cuticucho

Corani

Miguilla

Cat Arm

Botijlaca

Zongo #1

C D

Table 1: Selected impulse unit characteristics.

Unit Net Head (m) Power (kW) Speed (rpm) Mechanical time, secs Water time, secs T

Rank

Achachicala 414.5 895 429 5.04 1.59 0.425 0.227 6

Angostura 502.9 2,536 1,000 3.78 1.60 0.319 0.229 7

Botijlaca 370.3 2,238 750 3.11 0.72 0.184 0.072 9

Cat Arm 380.5 63,500 327 9.59 1.77 0.808 0.253 1

Corani 585.2 13,800 600 4.86 0.77 0.476 0.128 3

Cuticucho 650.7 2,425 1,000 3.09 0.93 0.450 0.232 4

Miguilla 457.2 1,492 1,000 6.45 1.33 0.714 0.251 2

Santa Rosa #1 198.1 4,500 429 3.00 0.69 0.437 0.173 5

Santa Rosa #2 792.5 6,714 750 3.77 0.59 0.187 0.049 8

Zongo #1 381.0 821 429 5.49 2.71 0.172 0.143 10

Rank based on largest T

ratio.

Above: Figure 1 – Chart showing relationship between T

, T

and T

for

impulse and reaction units. Area A – no frequency control possible; Area B

– frequency regulation on large systems only; Area C – frequency regulation

on small systems with small load changes; Area D – frequency regulation on

small systems with large load changes

WWW.WATERPOWERMAGAZINE.COM OCTOBER 2009 35

The ﬁrst hydro power development in Bolivia was at La Paz, where

a small single jet horizontal axis 1,200 HP impulse unit was com-

missioned in 1909 within the city at Achachicala. At the time, there

was no industrial load. Speed regulation was reasonable. The ﬁrst

development in the Zongo valley was also constructed at the same

time, but due to the excessively high penstock velocity of 9.08m/sec,

the unit had to be operated on base load.

Over time, further units were added at Achachicala, Zongo and

downstream at Botijlaca, which had to be operated manually to avoid

excessive frequency ﬂuctuations. More power plants were added

downstream at Cuticucho and Santa Rosa (2), but speed regulation

was difﬁcult, as the units all had slow needle jet opening times. When

a district dropped off line due to a fault, the only way to re-connect

was to manually intercept the jet ﬂow with the deﬂector at the largest

unit, the 9,000HP Santa Rosa #2, and then let the governor take over

by releasing manual control, on a telephone command, the instant the

district was re-connected. The weighted needle jet effective opening

time of all the hydro units on the La Paz system at that time was 9.2

seconds, far too slow to accommodate a signiﬁcant load-on due to

re-connection of a district.

The isolated Oruro system provides power for the tin mines around

Catavi. In 1931, two units of 2,000HP were installed at Miguilla,

and the speed regulation capability was much improved from that

experienced with Achachicala in La Paz. However, as the mining

load increased, a unit was added downstream at Angostura, but the

governing had to be manual, due to excessive speed deviations during

load-on demand from the mining equipment.

In 1968, two 18,500HP units were installed at Corani for the

Empresa Nacional de Electricidad, to provide power for the isolated

system at Cochabamba, where there is light industrial development,

(3). Speed regulation was found to be satisfactory.

From an inspection of Figure 1, it is evident that speed regulation with

impulse units improves as the ratio of unit start time to governor opening

time increases, as was experienced with reaction units. In Table 1, the

units are ranked according to their speed regulation capability, based on

the unit mechanical start time to jet opening time ratio. However, this

measure is not sufﬁciently accurate for design purposes.

I M P U L S E U N I T S P E E D C O N T R O L

Impulse units have two ﬂow controls – by the needle valve(s) which

control ﬂow, and by the jet deﬂector(s) which deﬂect the jet off the

runner. The needle valves can open rapidly, but always close slowly,

in order to limit penstock waterhammer. The jet deﬂector(s) move

very rapidly, usually in about 1.5 to 3 seconds to fully deﬂect the

jet(s) off the runner. The result is that speed rise on a full load-off is

very small compared to the speed rise in reaction units. Speed rise on

full load-off is usually less than 20%. Part load-off speed rise will be

much smaller. This is the main reason why impulse units can control

frequency with much smaller unit inertia than that required in reac-

tion units.

Speed drop on a 10% partial load-on from 50% to 60% load can

be calculated from the following equation derived from (4) -

N / N

= [1 - T / T

{1.2 -1.1 (1 - h

)

1.5

}]

0.5

[1]

The unknowns in Equation 1 are the part-load jet opening time T

and the negative waterhammer hw. The jet opening time can vary

considerably, is usually in the order of 4 to 60 seconds, and calculated

to produce a negative waterhammer between 40% and 20% or less.

The limiting criterion is the penstock proﬁle. If it has a “knee”, the

negative waterhammer may be limited to only a few percent, and the

jet opening time will be very long. In such cases, the unit will not be

capable of operating in an isolated mode. When there is no limitation

imposed by the penstock proﬁle, the negative waterhammer can be

large, and a fast opening time can be used.

The jet needle discharge characteristic has an “S” shape, with a

slow increase in ﬂow relative to stroke at the beginning and end of the

stroke. The slow start is imposed by the gradual curve of the needle,

required to avoid cavitation. The slow end is due to the smaller inner

diameters being opened at the end of the opening stroke. The most

rapid change in ﬂow with respect to stroke is in the middle range,

between about 20% and 70% stroke, and the relationship between

the effective opening stroke in the middle is about 0.6 times the full

stroke (T

= 0.6 T

). However, this relationship will vary slightly with

head and between manufacturers. The time required to complete a

10% increase in ﬂow from half-load will then be, including an allow-

TURBINES

Table 2: Selected impulse unit speed drop characteristics

Unit Penstock

length (m)

Max sound

wave a m/s

J ratio Waterham ratio

(N, I)

10% Jet time, T

Speed Drop % Regulation rank

New Old

Achachicala 1,532 1,352 2.50 0.134 I 0.90 2.83 5 6

Angostura 1,070 1,252 1.30 0.193 I 0.90 4.91 8 7

Botijlaca 406 1,216 1.14 0.141 N 1.20 6.48 9 9

Cat Arm 2,900 1,100 1.54 0.067 I 0.90 0.99 1 1

Corani 1,158 1,052 1.15 0.080 I 0.80 1.91 3 3

Cuticucho 1,207 1,207 1.08 0.098 I 0.60 2.53 4 4

Miguilla 1,323 1,243 2.54 0.130 I 0.73 1.76 2 2

Santa Rosa #1 330 1,070 1.07 0.225 I 0.60 4.60 7 5

Santa Rosa #2 1,274 1,224 1.05 0.060 I 1.40 3.73 6 8

Zongo #1 1,117 1,292 2.79 0.249 N 2.10 9.74 10 10

N = normal waterhammer, I = instantaneous waterhammer.

New regulation rank based on speed drop, old from Table 1.

Santa Rosa #1

Santa

Rosa #2

Angostura

Botijlaca

Zongo #1

Units in this area cannot provide

any form of speed control

Cuticucho

Corani

Miguilla

Achachicala

Cat Arm

Speed drop (%)

2 3 4 5 6 7 8 9 10

Unit start time (seconds)

Figure 2 – Chart showing relationship between unit start time and speed drop

on a nominal 10% load on from half load

36 OCTOBER 2009 INTERNATIONAL WATER POWER & DAM CONSTRUCTION

ance of 0.2 seconds to start the movement -

T = 0.2 + 0.1T

[2]

Combining equations 1 and 2 produces –

10% load-on = N / N

= [1 - (0.2 + 0.1T

)/ T

{1.2 - 1.1 (1 -

)

1.5

}]

0.5

. [3]

To calculate the negative waterhammer, the short time for the load

change must be taken into account; hence the instantaneous or regu-

lar waterhammer value may need to be used.

S P E E D R E G U L A T I O N A N A L Y S I S .

Equation 5 was used to calculate the 10% load-on speed drop for

the 25 units used in this analysis. For the 10 units listed in Table 1,

additional characteristics are provided in Table 2.

In Table 2, the units are ranked according to the speed drop on a

10% load-on, and the ranking from Table 1 is also shown. It is inter-

esting to note that the new regulation ranking is identical to the rank-

ing based on experience with reaction units, for the best 4 units. The

speed drops at Miguilla and Corani at less than 2% indicate that this

is about the limit for regulation of light industrial loads. Achachicala,

with a speed drop between 2% and 4% indicates that this is the range

for regulation for no industrial load, and at a speed drop of over 4%,

as indicated by Zongo, Angostura and Botijlaca, there is no speed

regulation, all conﬁ rming early operating experiences.

Another chart was developed to more clearly indicate the level of

regulation which could be provided by impulse units. This is shown

in Figure 2, where the 10% speed drop is plotted against the unit start

time. Two units, with valve opening times of more than 20 seconds

are missing on Figure 2, since their speed drop exceeds 10%. This

chart indicates that: for industrial loads, speed drop should be less

than 1%; for light industrial loads, speed drop should be less than

2%; for systems with no industrial load, speed drop should be less

than 4%; and systems with a speed drop over 4% cannot provide

any speed regulation.

To reduce the speed deviation, there are three alternatives avail-

able. These are listed in order of increasing cost –

1. Shorten the effective governor needle valve opening time as much

as possible. Assuming there are no restrictions imposed by a knee

in the penstock proﬁ le, the limit is reached at about 40% negative

waterhammer. Cost will be negligible.

2. Increase inertia. This could easily be accomplished by adding a ﬂ y-

wheel in a horizontal axis unit, or by increasing the rotor diameter

and weight in a vertical axis unit. Cost will increase slightly. For

a horizontal shaft unit, this will require an extra bearing, a longer

shaft, and more space will be needed in the powerhouse. For a

vertical axis unit, the rotor diameter and weight will increase.

3. Increase the penstock diameter and reduce the effective governor

opening time, to produce the same negative waterhammer. This

option would be very expensive, but friction would be reduced,

and energy increased. It is usually not an economic alternative.

Assuming that the needle opening time is as fast as possible, equation

3 can be re-written to determine the required inertia as -

= (0.2 + 0.1T

) {(N / N

)

– 1}

-1

{1.2 - 1.1 (1 - h

)

1.5

} [4]

With a deﬁ ned speed variation of 1%, 2% and 4%, equation 4 can

be revised to -

= k (0.2 + 0.1T

) {1.2 - 1.1 (1 - h

)

1.5

} [5]

Where k is a factor depending on the desired degree of regulation,

and has a value of –

U 49 or more for industrial loads,

U between 24 and 49 for light industrial loads,

U between 12 and 24 for isolated units with no industrial loads.

U less than 12, will not provide any speed regulation.

This analysis is not applicable to small units with capacities less than

about 1000kW. For such units, speed control can be provided by using

a dump load such as water heaters, wherein the power is electronically

diverted to the dump load whenever there is a surplus. A governor is not

required, since water ﬂ ow is maintained at a constant level.

C O N C L U S I O N S

A review of operating experience with isolated impulse turbine systems

in Bolivia, has indicated that by calculating the speed drop on a nominal

10% load change, from 50% load to 60% load, the extent of speed drop

will indicate the unit’s ability to control frequency. A speed drop of 1%

or less deﬁ nes a unit capable of accepting industrial load changes. A unit

with a speed drop of between 1% and 2% could be used on an isolated

system with light industrial load changes. At a speed drop of between

2% and 4%, the unit would only be suitable for isolated systems with

no industrial loads. A speed drop in excess of 4% indicates that the unit

would not contribute to frequency regulation.

The most economic method of improving speed regulation is to

ﬁ rst decrease the needle jet opening time as much as possible, and

then increase inertia with a ﬂ ywheel in horizontal axis units, or by

adding inertia to the generator rotor in vertical axis units.

J. L. Gordon, Hydropower Consultant, 102 Blvd St-Jean,

Pointe Claire, Quebec, Canada, H9S 4Z1. Fax/tel: +1 514

695 2884. Email: jim-gordon@sympatico.ca

TURBINES

References

(1) Gordon, J. L. and Whitman, D. H. 1985 Generator inertia for isolated

power systems. Canadian Journal of Civil Engineering, 12(4): 814-820.

(2) Encinas, L. and Ebenstein, G. L. Una cascada de plantas intercepta at

Zongo en Bolivia. Ingenieria Internacional Construccion, 1968, (12): 53-58.

(3) Zenteno, M., Williams, A. W. and Gordon, J. L. 1982. The expansion of

two Bolivian plants. Water Power and Dam Construction, Vol. 34 (2): 26-31.

(4) Gordon, J. L. and Smith, W. G. 1961. Speed regulation for hydraulic

turbines. The Engineering Journal, 44 (10): 92-97.

List of symbols

a sound wave velocity in meters per second.

g acceleration due to gravity, in meters per second squared.

generator inertia, in tonne-meters squared, based on diameter

of rotating mass.

h turbine rated head in meters.

water hammer ratio, expressed as a fraction of h.

J ratio of actual to normal inertia, ranges between 0.9 and about 3.0.

k a coefﬁ cient deﬁ ning the required speed regulation for an impulse unit.

kW generator rating, in kilowatts.

N synchronous speed, in revolutions per minute.

speed at end of load change, in revolutions per minute.

T needle valve opening time required for a part load change, in seconds.

effective needle valve opening time, in seconds.

total needle valve opening time, in seconds.

mechanical start time of unit, in seconds = 0.00274 (GD)

/ (kW)

water column start time, in seconds = LV/(gh)

IWP& DC

ARMAC is Montanhydraulik‘s computer-

controlled ﬂ ow-level-regulation and control

system, operating successfully in many hydro

dam projects in India. It measures water inﬂ ows

into the reservoir every 15 minutes. Using 80-

to 100-year water ﬂ ow data, it works out the

optimum combinations of water levels and

gate openings for the speciﬁ c time of year,

and commands the gates to open or close.

ARMAC can also be used to regulate flows

through several reservoirs and dams on the same

river, communicating the data, including hydraulic

system health, via VSAT or GPRS.

ARMAC is part of Montanhydraulik‘s turnkey

solutions for hydromechanical and electrohydrau-

lic systems. We offer the complete system with

hydraulic cylinders, aggregates, electrical control

and installation.

INTELLIGENT POWER

www.mont anhydraulik.com

Montanhydraulik Group

„100 years

of data for today‘s

flow-level

regulation“

38 OCTOBER 2009 INTERNATIONAL WATER POWER & DAM CONSTRUCTION

IRRIGATION

USTRALIAN agriculture is highly dependant on farm

dams. Storage sizes range from a few megalitres (ML)

for stock and domestic supplies to larger dams used for

commercial irrigation. Conservative estimates suggest

that in excess of 8 million ML is stored in farm dams (ie. 9% of

total stored water), and that there are more than 2 million farms

dams across Australia. Evaporation from bulk distribution chan-

nels in regulated irrigation systems also amounts to a signiﬁcant

loss. Annual evaporation losses from these storages are estimated

to be around 1.32GL/yr and up to 2.88GL/yr. It is important to

quantify evaporation losses from storages in order to assess the

feasibility of investing in evaporation mitigation technologies.

M E A S U R I N G L O S S E S F R O M F A R M D A M S

It is difﬁcult to accurately measure evaporation from an open storage.

Evaporation of a free water surface is the result of complex processes

affected by incident solar radiation, wind speed, air temperature and

humidity, and the energy stored in the water body, especially surface

water temperature.

A water balance approach provides a practical approach for esti-

mating aggregate losses due to evaporation. For periods when there

is no inﬂow, outﬂow or rainfall and for small incremental time steps

when surface area is constant, the net change in evaporation and

seepage can be determined by measuring changes in water depth.

The accuracy of this method depends greatly on the accuracy of the

equipment used to measure the change in water depth. Monitoring

systems and data analysis techniques have recently been commercial-

ised by Aquatech Consulting as the Irrimate Seepage and Evaporation

Meter. This uses an accurate pressure sensitive transducer to measure

changes in water level every 15 minutes. Rainfall, wind velocity and

water temperature are also logged for use in the analysis which are

achieved using software developed by the CRC for Irrigation Futures

through the National Centre for Engineering in Agriculture.

There are a wide range of products available for controlling evapo-

ration loss. These systems include:

Reducing evaporation losses

Annual evaporation losses from irrigation

storage dams and channels are signiﬁcant

across Australia. Erik Schmidt gives an

overview of the mitigation technologies

that can be employed to reduce such losses

A modular system can typically provide up

to 90% savings for 100% of the area of water covered

Shade cloth structures can come in a range of UV ratings

WWW.WATERPOWERMAGAZINE.COM OCTOBER 2009 39

IRRIGATION

U Continuous ﬂ oating covers.

U Modular covers.

U Shade structures.

U Chemical covers

Continuous ﬂ oating covers

Continuous ﬂ oating plastic covers act as an impermeable barrier that ﬂ oats

on the water surface and can achieve above 90% evaporation savings for

full cover of the dam. Most of these products have a high capital cost and

replacement life varies (typically between 10 and 20 years). The structural

integrity of the product under windy conditions and ﬂ uctuating water levels

is important. Water quality can be impacted by reduced dissolved oxygen,

light penetration and change in water temperature. This can have a positive

impact on reducing algal growth. Signiﬁ cant difﬁ culties can be encountered

with installation on large storages above 5ha. In some cases these covers can

be deployed as a series of large rafts covering up to 1ha.

Modular systems

Modular ﬂ oating covers come in a range of sizes typically up to 3m

in area and act in a similar manner to ﬂ oating covers. However they

do not have the structural challenges of a continuous sheet. Modular

ﬂ oating covers can also be deployed to cover only a portion of the

storage, for example that portion always holding water.

Modules can be free-floating or connected together to form a

larger raft. Modules are typically made from a plastic material and

can generally provide up to 90% savings for 100% area covered. The

actual area covered will depend on the number, shape and size of the

module and storage characteristics.

Generally these systems have a very high capital cost (in excess of

US$17/m

). Repair and replacement of modules is possible and water

quality impacts will depend on the relative area covered, oxygen

transfer and changes to water temperature.

Shade structures

Shade structures in general are suspended above the water surface using

cables creating a web-like structure with shade cloth ﬁ tted between the

cables. The shade cloth can come in a range of UV ratings (to describe

the amount of UV blocked by the shade cloth). Evaporation savings of

70 to 80% have been demonstrated in trials.

Floating shade cloth modules or rafts have recently been marketed.

Most of these products have a relatively high capital cost. In general shade

structures are not as effective in reducing evaporation as ﬂ oating covers.

They allow free ﬂ ow of oxygen to the water, although wind velocity

and wave action will be reduced, which impacts dissolved oxygen levels.

Algae may be reduced owing to less light penetration.

Chemical covers

Chemical covers have been promoted as a low cost method to reduce

evaporation losses. Some products are true monolayers (ie a single

molecule thick) while others are multiple layers with different water

saving characteristics and water quality impacts. These products are

generally biodegradable and there is a need to reapply frequently

(between three and ten days). Water savings have been shown to be

highly variable, from less than 10% to up to 50% and are impacted

by prevailing wind, temperature and water quality.

True monolayers are applied at very low application rates and rely

on the self spreading ability of the chemical. Advantages of these

products are the low capital cost and choice to apply only when

needed. Monolayers offer much potential for affecting evaporation

savings but inconsistent evaporation saving performance has lim-

ited their adoption in Australia. It has been recognised that further

research is needed and the Cooperative Research Centre for Irrigation

Futures (CRC-IF) is currently working on such a project.

The key objectives of the project are to:

U Develop standardised methods for evaporation and seepage monitor-

ing of storage dams based on depth sensing technologies, analysis pro-

cedures and use of meteorological based evaporation estimates.

U Improve understanding of the monolayer product performance and

factors affecting this performance.

U Develop improved monolayer products.

U Develop monolayer application, monitoring and control systems

and recommendations for best management practice.

E C O N O M I C V I A B I L I T Y

The cost beneﬁ t of evaporation control is a key driver in investment

in the technologies described above. The potential cost of installing

and operating an evaporation control product per unit of water saved

($/ML) will be a function of:

U Installation and maintenance costs which are very dependent on site

situation and installation issues.

U Annual and seasonal evaporation losses from storages at the location.

U Efﬁ ciency of the evaporation mitigation technology.

U Storage operating conditions.

This needs to be compared with the value of water to the landholder

in terms of increased crop production, the cost of water to be pur-

chased or the potential to trade water surplus. A ready reckoner has

been developed by the CRC for Irrigation Futures to help undertake

such an economic analysis. For more details log onto http://www.

readyreckoner.ncea.biz

Erik J Schmidt, CRC for Irrigation Futures, National

Centre for Engineering in Agriculture, University of

Southern Queensland, Australia

IWP& DC

Above left to right: A continuous ﬂ oating cover can last for 10-20 years;

Irrimate Seepage and Evaporation Meter; A modular system can typically

provide up to 90% savings for 100% of the area of water covered

Right: More research is being carried out to optimise the performance of

chemical monolayers

40 OCTOBER 2009 INTERNATIONAL WATER POWER & DAM CONSTRUCTION

PLANNING & PROJECTS

HE Red River ﬂows northward at a minimal slope as it

traverses the relatively ﬂat terrain between North Dakota

and Minnesota in the US. As the snow melts and the rains

begin each spring, the rising water challenges the river’s

capacity. At least once a year, the Red River overﬂows its banks.

Most of these ﬂoods are minor. However, in 1997, an extreme

set of conditions conspired to create the region’s most disastrous

ﬂood since 1826. Heavy winter snowfall, ﬂuctuating spring tem-

peratures, early spring rains and an April blizzard caused unprec-

edented runoff into the Red River Basin. Rising river levels caused

extensive backﬂow into tributaries, and the riverbanks and sup-

porting systems simply could not contain the increased water

volume. Floodwaters crested at a record 17m in Grand Forks,

North Dakota, and reached 4.8km inland there and in the twin city

of East Grand Forks, Minnesota.

Approximately 60,000 residents

were forced to evacuate their homes;

some never returned. Damage from the

ﬂood totalled US$3.5B.

This event highlighted the need for improved

elevation data throughout the Red River Basin

to help scientists and decision makers better under-

stand, predict and respond to future ﬂood events. “The

1997 ﬂood was an unprecedented and historic event that

stressed – and in some cases exceeded – the mathematical

limits of ﬂood-modelling software as well as our understanding

of ﬂoods in this region,” explains Charles Fritz, director of the

International Water Institute (IWI).

The devastation caused by the ﬂood sparked the creation of the

Red River Basin Mapping Initiative, a US$5M programme that was

ofﬁcially launched in May 2008 to collect high-accuracy elevation

data over the entire US portion of the Red River Basin using airborne

LiDAR mapping technology.

“Much of the uncertainty in current forecasting models is related

Advances in LiDAR data collection technology can help decision makers better

understand, predict and respond to future ﬂood events in the US’ Red River

Basin. David A Webb explains

Flood control from the air

Right: This 3D perspective view of the LiDAR data shows how the river has

meandered over the years. The dark green is the current river channel

Below: Ground survey points are being used to supplement airborne GPS for

the airborne LiDAR and imagery acquisition

Water Power and Dam Construction - Issue October 2009

Подождите немного. Документ загружается.