Wang X. Vehicle Noise and Vibration Refinement

Подождите немного. Документ загружается.

Random signal processing and spectrum analysis

in vehicle noise and vibration reﬁ nement

X. WANG, RMIT University, Australia

Abstract: Starting from deﬁ nitions of a linear system, random data and

process, the statistical properties of random data, correlation analysis,

spectral analysis, the Fourier transform, the impulse response function

and the frequency response function are introduced. The digital FFT

analysis process is illustrated. The relationships between the correlation

function and the power density spectrum function, between the impulse

response function and the frequency response function, and between the

Fourier spectrum function and the power spectrum function are

established. The deﬁ nition and physical meaning of the coherence

function are illustrated. Frequently encountered random signals and

their conversions are demonstrated.

Key words: random data, time-history record, ensemble, stationary,

non-stationary, ergodic, non-ergodic, time-averaging, expected value,

mean square value, variance, standard deviation, probability distribution,

Gaussian distribution, Rayleigh distribution, correlation analysis,

autocorrelation, cross-correlation, Fourier series, Fourier transform,

digital FFT analysis, sampling frequency, spectrum size, windowing,

anti-alias ﬁ ltering, sampling points, Fourier spectrum, FFT versus time

spectrum, spectral density function, power spectrum density function,

auto-power spectrum density function, cross-power spectrum density

function, impulse response function, frequency response function,

coherence function, linear system, additive property, homogeneous

property, superposition principle, convolution integral.

5.1 Random data and process

Random data are any type of data occurring especially in vehicle tyre–road

induced noise and vibration that do not have an explicit mathematical

formula to describe their properties. It is impossible to predict the precise

level of the disturbance at any given time and hence it is impossible to

express such disturbances as continuous functions in the time domain – only

statistical representations are possible. Any time-history record represents

only one record out of a collection of different time-history records that

might have occurred. From the vibration point of view, the frequency

content of a random signal is very important. For example, the frequency

spectrum of a road input to a vehicle is a function of the spatial random

Copyrighted Material downloaded from Woodhead Publishing Online

Delivered by http://woodhead.metapress.com

ETH Zuerich (307-97-768)

Sunday, August 28, 2011 12:04:14 AM

IP Address: 129.132.208.2

94 Vehicle noise and vibration reﬁ nement

proﬁ le of the road surface and the speed of the vehicle. For a given set of

conditions, it results in a large number of frequency components distributed

over a wide band of frequencies.

5.1.1 Deﬁ nition of terms

As shown in Fig. 5.1, an ensemble is deﬁ ned as a collection of records.

A random process is deﬁ ned as a process which is represented by the

ensemble and deﬁ ned by analysing various statistical properties over the

ensemble.

Stationary random data is deﬁ ned as data whose ensemble-averaged

statistical properties are invariant with time. For such data, ensemble-

averaged mean values are the same at every time. For vehicle applications,

stationary processes include idle conditions, constant-speed driving or

cruise control driving conditions. Ergodic data is stationary random data

where one long-duration average on any arbitrary time-history record gives

results that are statistically equivalent to associated ensemble averages over

a large collection of records. In practice, stationary random data will auto-

matically be ergodic if there are no sine waves or other deterministic phe-

nomena in the records. Classiﬁ cation of random systems is shown in Fig.

5.2. For example, a white noise, wideband random signal is stationary and

ergodic. For such data, one long-duration experiment is sufﬁ cient to obtain

useful information, as a stationary random record should never have a

beginning or an end.

(t)

+ t

5.1 Ensemble of time-history records deﬁ ning a random process.

Copyrighted Material downloaded from Woodhead Publishing Online

Delivered by http://woodhead.metapress.com

ETH Zuerich (307-97-768)

Sunday, August 28, 2011 12:04:14 AM

IP Address: 129.132.208.2

Random signal processing and spectrum analysis 95

Non-stationary random data is deﬁ ned as data whose ensemble-averaged

statistical properties change with time. Transient random data is a special

class of non-stationary random data with a clearly deﬁ ned beginning and

end to the data, for example vehicle second/third gear slow acceleration,

ﬁ rst gear wide open throttle (WOT) acceleration, overrun/coastdown

deceleration processes, braking, cornering, etc.

When stationary random data pass through constant-parameter linear

systems, the output data will also be stationary. When transient random

data pass through constant-parameter linear systems, the output will be

transient random data. However, when stationary or transient random data

pass through time-varying linear systems, the output will be non-stationary.

In general, techniques for analysing stationary random data are not appro-

priate for analysing non-stationary random data.

5.1.2 Time-averaging and expected value

In random data, we often encounter the concept of time-averaging over a

long period of time:

xt xt

xt t

()

→∞

∫

lim

(5.1)

or the expected value of x(t), which is:

Ext

xt t

(

)

[]

(

)

→∞

∫

lim

(5.2)

In the case of discrete variables x

, the expected value is given by:

[]

→∞

∑

lim

(5.3)

Random

Stationary

Non-stationary

Non-ergodic

Special types of non-stationary

data

Ergodic

5.2 Classiﬁ cation of random systems.

Copyrighted Material downloaded from Woodhead Publishing Online

Delivered by http://woodhead.metapress.com

ETH Zuerich (307-97-768)

Sunday, August 28, 2011 12:04:14 AM

IP Address: 129.132.208.2

96 Vehicle noise and vibration reﬁ nement

5.1.3 Mean square value

The mean square value, designated by

()

or E[x

(t)], is found by integrat-

ing x

(t) over time interval T and taking its average value according to:

Ex t x

xt t

22 2

(

)

[]

()

(

)

→∞

∫

lim d

(5.4)

5.1.4 Variance and standard deviation

An important property describing the ﬂ uctuation in ensemble is the vari-

ance σ

, which is the mean square value about the mean, given by:

=−

(

)

→∞

∫

lim

xx td

(5.5)

By expanding, you can determine that:

=−

()

()xx

(5.6)

so that the variance is equal to the mean square value minus the square

of the mean. The positive square root of the variance is the standard devia-

tion σ.

5.1.5 Probability distribution

Refer to the random data in Fig. 5.3. A horizontal line at the speciﬁ ed value

is drawn and the time interval Δt

(i = 1, 2, 3 . . .) during which x(t) is less

than x

is summed and divided by the total time, which represents the frac-

tion of the total time that x(t) < x

. The probability density that x(t) will be

found less than x

is:

Px x Px

()

−

()

→

lim

(5.7)

1. 0

Δt

P(x)

x(t)

5.3 Calculation of cumulative probability.

Copyrighted Material downloaded from Woodhead Publishing Online

Delivered by http://woodhead.metapress.com

ETH Zuerich (307-97-768)

Sunday, August 28, 2011 12:04:14 AM

IP Address: 129.132.208.2

Random signal processing and spectrum analysis 97

From Fig. 5.4 you can see that p(x) is the slope of the cumulative probability

distribution P(x):

Px px x

(

)

(

)

∫

(5.8)

The area under the probability density curve of Fig. 5.4(b) between two

values of x represents the probability of the variable being in this interval.

Because the probability of x(t) being between x = ±∞ is certain:

Ppxx()+∞ =

(

)

−∞

∞

∫

(5.9)

and the total area under p(x) must be unity.

The mean and mean square value deﬁ ned in terms of the time average

are related to this probability density function in the following manner. The

mean value

coincides with the centroid of the area under the probability

density curve p(x), as shown in Fig. 5.4(b), and can be determined by the

ﬁ rst moment:

xxpxx=

(

)

−∞

∞

∫

(5.10)

The mean square value is determined from the second moment:

xxpxx

()

(

)

−∞

∞

∫

(5.11)

Δx

ΔP

p(x)

(a)

(b)

1. 0

P(x)

5.4 (a) Cumulative probability; (b) probability density.

Copyrighted Material downloaded from Woodhead Publishing Online

Delivered by http://woodhead.metapress.com

ETH Zuerich (307-97-768)

Sunday, August 28, 2011 12:04:14 AM

IP Address: 129.132.208.2

98 Vehicle noise and vibration reﬁ nement

which is analogous to the moment of inertia of the area under the probabil-

ity curve about x = 0.

The variance σ

is deﬁ ned as the mean square value about the mean:

=−

(

)

(

)

(

)

−

(

)

(

)

(

)

−∞

∞

−∞

∞

−∞

∞

−∞

∞

∫∫

∫

x x px x xpx x

x xpx x x px

∫∫

(5.12)

()

−

(

)

(

)

()

−

(

)

xxxxx

(5.13)

5.1.6 Gaussian and Rayleigh distributions

The Gaussian and Rayleigh distributions frequently occur in vehicle noise

and vibration data. The Gaussian distribution is a bell-shaped curve sym-

metric about the mean value:

px e

(

)

−

()

(5.14)

The expected value of the product of four Gaussian random process vari-

ables, E[x

, x

], the fourth moment of the Gaussian random inputs,

can be reduced to the products of the expected values of two process

variables:

Ex x x x Exx Exx Exx Exx

Exx Exx

1 2 3 4 12 34 13 24

14 23

,,,

[]

[][]

[][]]

− 2

1234

μμμμ

(5.15)

where μ

is the mean value of the x

process (i = 1, 2, 3, 4). In most Gaussian

random processes, μ

= 0 (i = 1, 2, 3, 4).

Random variables restricted to positive values, such as the absolute value

A of the amplitude, often tend to follow the Rayleigh distribution, deﬁ ned

as:

pA A

(

)

(

)

⎧

⎨

⎪

⎩

⎪

−

()

(5.16)

The shape is shown in Fig. 5.5. The mean and mean square values for the

Rayleigh distribution can be found from the ﬁ rst and second moments:

Copyrighted Material downloaded from Woodhead Publishing Online

Delivered by http://woodhead.metapress.com

ETH Zuerich (307-97-768)

Sunday, August 28, 2011 12:04:14 AM

IP Address: 129.132.208.2

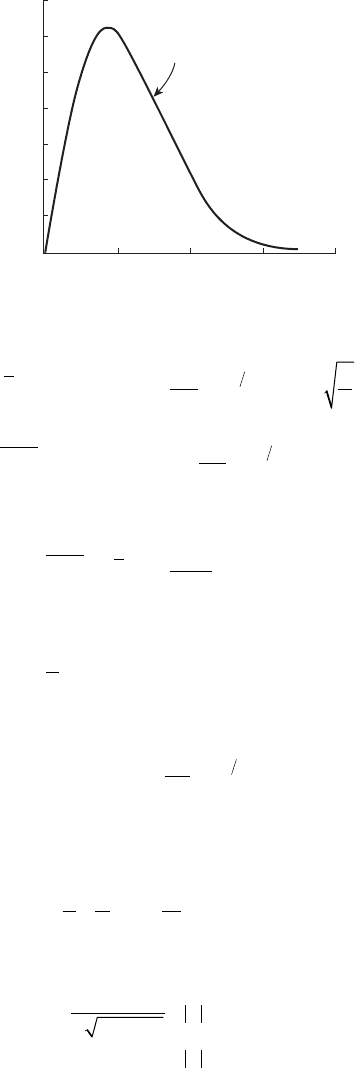
Random signal processing and spectrum analysis 99

AApAA

(

)

∞

−

()

∞

∫∫

ded

(5.17)

AApAA

()

(

)

∞

−

()

∞

∫∫

ded

(5.18)

The variance associated with the Rayleigh distribution is:

()

−

()

−

(

)

(5.19)

i.e.

≈

(5.20)

The probability of A exceeding a speciﬁ ed value λσ is:

prob e dA

[]

∞

−

()

∫

λσ

(5.21)

The cumulative probability distribution for a sine wave is shown in the ﬁ rst

column of the table in Fig. 5.6, and is written as:

(

)

(

)

−

sin

(5.22)

Its probability density is:

px x A

(

)

−

(

)

⎧

⎨

⎪

⎩

⎪

(5.23)

Rayleigh distribution

01234

(A)

0.6

0.5

0.4

0.3

0.2

0.1

5.5 Rayleigh distribution.

Copyrighted Material downloaded from Woodhead Publishing Online

Delivered by http://woodhead.metapress.com

ETH Zuerich (307-97-768)

Sunday, August 28, 2011 12:04:14 AM

IP Address: 129.132.208.2

100 Vehicle noise and vibration reﬁ nement

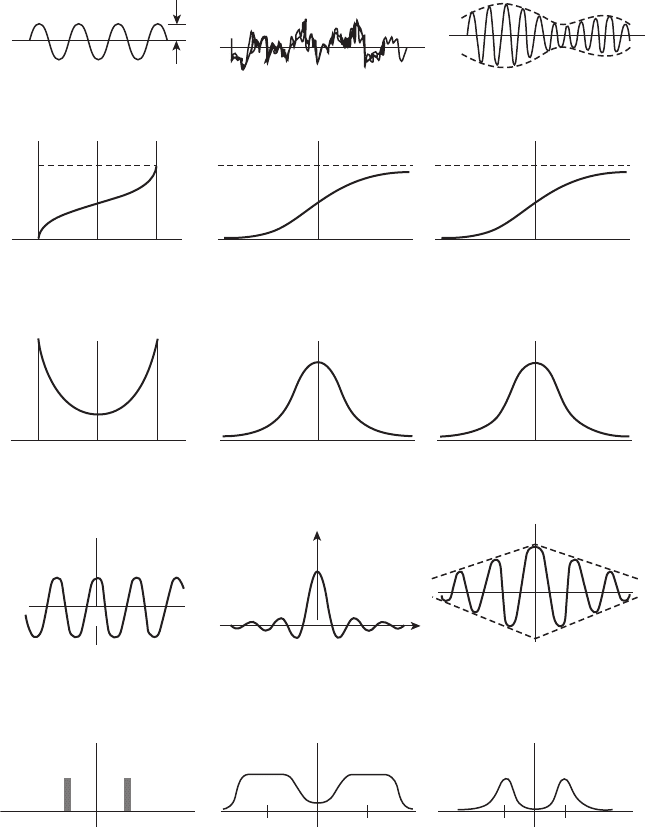
5.6 Three frequently encountered signals and their conversions.

Sine wave

Autocorrelation

Autospectrum Autospectrum Autospectrum

Wideband record

1. 0 1. 0

–A

A00

–A

Narrowband record

P(x) P(x)

p(x)

R(t)

(w)

R(t) = –cos w

–w

Area = –

–w

(w) S

(w)

Area = –

R(t) = ce

–k/t

p(x)

1. 0

P(x)

5.2 Correlation analysis

Correlation analysis consists of autocorrelation and cross-correlation

analysis. It is a type of analysis in the time domain.

Copyrighted Material downloaded from Woodhead Publishing Online

Delivered by http://woodhead.metapress.com

ETH Zuerich (307-97-768)

Sunday, August 28, 2011 12:04:14 AM

IP Address: 129.132.208.2

Random signal processing and spectrum analysis 101

5.2.1 Autocorrelation

Correlation is a measure of the similarity between two quantities. Suppose

two records x

(t) and x

(t) in one ensemble/collection are as shown in Fig.

5.7. The autocorrelation is deﬁ ned as:

R Extxt xtxt

xtxt t

WWW W

()

[]

()

→∞

−

∫

lim

(5.24)

When τ = 0:

Rx0

(

)

()

(5.25)

where the random process has a mean of zero. R(τ) = R(−τ) is symmetric

about the origin τ and the vertical axis which is an even function of τ as

shown in Fig. 5.6. Figure 5.8 shows the block diagram of an autocorrelation

analyser.

5.2.2 Cross-correlation

Consider two random quantities x(t) and y(t). The cross-correlation between

them is deﬁ ned as:

x(t)

(t)

x(t + t)

5.7 Correlation between x(t) and x(t + τ).

Copyrighted Material downloaded from Woodhead Publishing Online

Delivered by http://woodhead.metapress.com

ETH Zuerich (307-97-768)

Sunday, August 28, 2011 12:04:14 AM

IP Address: 129.132.208.2

102 Vehicle noise and vibration reﬁ nement

R Extyt xtyt

xtyt t

WWW W

()

[]

()

→∞

−

lim

∫

(5.26)

5.3 Fourier series

Generally, random time functions contain oscillations of many frequencies,

which approach a continuous spectrum. Although random time functions

are generally not periodic, their representations by Fourier series, in which

the periods are extended to a large value approaching inﬁ nity, offers a

logical approach.

The exponential form of the Fourier series is shown to be:

xt c c c c

()

==+ +

()

−∞

∞

−

∞

∑∑

eee

ZZZ

111

(5.27)

This series, which is a real function, involves a summation over negative

and positive frequencies and also contains a constant c

. c

is the average

value of x(t) and because it can be dealt with separately we exclude it in

future considerations. Moreover, actual measurements are made in terms

of positive frequencies, so it would be more desirable to work with:

xt c

()

⎡

⎣

⎢

⎤

⎦

⎥

∞

∑

Re e

(5.28)

where:

ata tbtbt

(

)

=+ + ++ + +

1122 1122

cos cos sin sin

ωω ωω

……

(5.29)

and ω

= 2π/T, ω

= nω

and c

= a

/2.

Multiplier

Time

delay t

Integrator

and

averager

R(t)

x(t + t)

x(t)x(t + t)

x(t)

5.8 Autocorrelation analyser block diagram.

Copyrighted Material downloaded from Woodhead Publishing Online

Delivered by http://woodhead.metapress.com

ETH Zuerich (307-97-768)

Sunday, August 28, 2011 12:04:14 AM

IP Address: 129.132.208.2