Вісник Харківського національного технічного університету сільського господарства імені Петра Василенка. Вип. 107. Механізація сільськогосподарського виробництва. Том 2

Подождите немного. Документ загружается.

111

піврами трактора від прямолінійної траєкторії та витрати палива.

Обчислення та накопичення статистичної інформації відбувається в

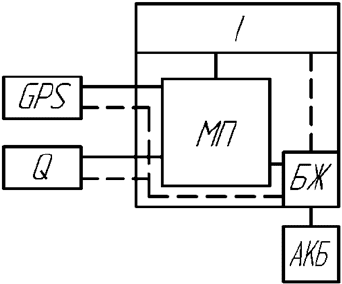
мікропроцесорі МП, а результат виводиться на індикаторі І (рис. 1). Дані

амплітуди відхилення та траєкторії руху надходять від навігаційного пристрою

GPS. Також МП з’єднаний з датчиком витрати палива Q для отримання

інформації про витрату палива. Блок живлення БЖ перетворює бортову

напругу трактора або акумуляторної батареї АКБ в напругу, необхідну для

вузлів пристрою.

В якості датчика витрати палива використовується модифікований

витратомір палива ИП-179. Курсопоказчик Trimble EZ-Guide 250 виконує

функцію навігаційного пристрою. Також на блоці з мікропроцесором

розташовується інтегральний гіроскоп ADXRS300 [3].

В пам’яті пристрою фіксуються та відображаються на екрані: довжина гону,

координати початку та кінця гону, витрата палива, амплітуда відхилення. При

послідуючих проходах агрегату по полю на індикаторі додатково відображаються

(відносно до попереднього проходу): витрата палива, довжина гону, амплітуда

відхилення.

Пристрій видає попереджуючий сигнал у випадках: довжина гону

збільшилась відносно до попереднього проходу на 10% і вище, амплітуда

відхилення збільшилась відносно до попереднього проходу на 10% і вище,

амплітуда відхилення та довжина пройденого шляху поступово зростають на 7,5% і

вище на кожному проході відносно першого проходу, витрата палива збільшилась

відносно до попереднього проходу на 10% і вище, витрата палива поступово

зростає на 7,5% і вище на кожному проході відносно першого проходу.

Рис. 1 – Блок-схема пристрою контролю за траєкторією руху та витратою палива мобільного

енергетичного засобу:

GPS – навігаційний пристрій; Q – датчик витрати палива; МП – мікропроцесор;

І – індикатор; БЖ – блок живлення; АКБ – акумуляторна батарея.

Пристрій працює наступним чином. На технічно справний трактор після

проведення ЩТО встановлюється пристрій контролю за траєкторією руху та

витратою палива. В настройки пристрою вноситься режим керування агрегатом

(за нечітко вираженим орієнтиром, за чітко вираженим орієнтиром або за

курсопоказчиком).

Агрегат виїжджає в поле та перед початком першого проходу тракторист натис-

кає кнопку на пристрої. Кінець гону тракторист відмічає натисканням кнопки (рис. 2).

112

Рис. 2 – Розташування пристрою контролю за траєкторією руху та витратою палива в кабіні

трактора ХТЗ-150К-09: 1 – індикатор; 2 – кнопка керування.

Таким чином розроблений пристрій попереджає тракториста при

збільшенні амплітуди відхилення та довжини гону, поступового збільшення

цих показників, а також при збільшенні витрати палива. При появі

попереджуючого сигналу тракторист повинен змінити режим руху агрегату або

провести технічне обслуговування та при необхідності – ремонт елементів

агрегату.

Дослідження системи контролю за траєкторією руху та витратою палива

виконувались в агрофірмі ФГ «Восход» Сахновщанського району, Харківської

області на ґрунтообробно-посівному агрегаті в складі трактора ХТЗ-150К-09 та

сівалки прямої сівби АПП-6. При дослідженнях визначались наступні

показники: швидкість руху агрегату, відхилення траєкторії руху першої

піврами трактора від прямої лінії, витрата палива та час виконання

технологічного процесу.

Результати польових досліджень пристрою контролю за траєкторією руху

та витратою палива наведені в табл. 1.

Таблиця 1 – Результати польових досліджень системи контролю за траєкторією руху

та витратою палива

Спосіб

керування

Показники

Агрегат ХТЗ

150К

09 + АПП

базовий

з системою

контролю

в, % до базового

На не чіткий

орієнтир

Витрата палива Q, мг

95,318

12,315

68,302

73,298

9,94

8,94

Амплітуда

відхилення у, м

77,0

75,0

0,695

0,668

90,3

89,1

Погектарна витрата

палива G, кг/га

22,300 21,163 94,9

На чіткий

орієнтир

Витрата палива Q, мг

40,285

20,283

73,270

42,268

86,94

78,94

Амплітуда

відхилення у, м

52,0

51,0

493,0

484,0

85,94

81,94

Погектарна витрата

21,120

20,022

94,8

113

палива

, кг/га

Примітка. Над рискою середнє значення показника, під рискою

максимальне значення показника

Як видно з табл. 1, використання пристрою контролю за траєкторією руху

та витратою палива зменшує погектарну витрату та витрату палива на гоні

100 м в середньому на 5,2%, а амплітуду відхилення – на 11%.

Висновки. Використання системи забезпечило в господарстві зниження

експлуатаційних витрат у 2009 р. від впровадження пристрою контролю за

траєкторією руху та витратою палива на сівбі озимих культур на 12,0 грн/га та

2545,32 грн на один агрегат. Доцільно запровадити цей пристрій на трактора в

сільських господарствах України.

Список використаних джерел

1. Антощенков Р. В. Підвищення ефективності експлуатації комбінованих

ґрунтообробно-посівних агрегатів: Автореф. дис. канд. техн. наук:

05.05.11 / ХНТУСГ ім. П.Василенка. – Х., 2010. – 20 с.

2. Рославцев А.В. Результаты исследования движения МТА /

А.В. Рославцев, С.Л. Абдула // Тракторы и сельхозмашины. – 1999. – №

10. – с. 14-18.

3. Cистема контролю за траєкторію руху та витратою палива. Патент

України № 51162, опубл. В бюл. № 13, 2010 // Мазоренко Д. І. та ін.

Аннотация

МЕХАТРОННАЯ ИНФОРМАЦИОННАЯ СИСТЕМА

МАШИННО-ТРАКТОРНОГО АГРЕГАТА

Антощенков Р., Ковалёв Р.

В работе исследована мехатронная информационная система машинно-

тракторного агрегата.

Abstract

MECHATRONIC INFORMATION SYSTEM OF MACHINE-TRACTOR

AGGREGATE

R. Antoshchenkov, R. Kovalyov

Mechatronic information system of machine-tractor aggregate investigated in

this article.

114

УКД 631.35:621.225: 621.891

ОЦЕНКА ВЛИЯНИЯ НЕСУЩЕЙ СПОСОБНОСТИ СМАЗОЧНОЙ

ПЛЕНКИ РАБОЧЕЙ ЖИДКОСТИ НА ВЫХОДНЫЕ ПАРАМЕТРЫ

ОБЪЕМНОГО ГИДРОПРИВОДА ТРАНСМИССИЙ

СЕЛЬСКОХОЗЯЙСТВЕННЫХ МАШИН

Косолапов В.Б., к.т.н., доц.

Харьковский национальный автомобильно-дорожный университет

Литовка С.В., ассист.

Харьковский национальный технический университет сельского хозяйства

имени Петра Василенка

Выполнены экспериментальные исследования влияния несущей

способности смазочной пленки рабочей жидкости (РЖ) на скорость

изменения объемного коэффициента полезного действия (КПД) гидромотора

объемного гидропривода трансмиссии (ОГТ) сельскохозяйственных машин

(СХМ). Показано, что уменьшение несущей способности смазочной пленки РЖ

в процессе эксплуатации СХМ определяет, при прочих равных условиях,

увеличение скорости изменения объемного КПД гидромотора ОГТ.

Введение. Важным условием повышения эксплуатационных характеристик

сельскохозяйственных машин (СХМ) является применение гидроприводов. В

настоящее время в конструкциях СХМ широко применяются гидравлические

исполнительные механизмы для привода рабочих органов, в системах управления,

а также в качестве привода трансмиссий. Применение ОГТ является важным

условием повышения эксплуатационных характеристик СХМ [1].

Анализ публикаций. По данным многочисленных исследований

установлено, что до 70% отказов в работе гидронасыщенных мобильных машин

приходится на долю гидропривода [2, 3].

Трансмиссия широко используемого зерноуборочного комбайна Дон-

1500 оснащена объемным гидроприводом типа ГСТ-90 [4]. В процессе

эксплуатации привода трансмиссии по мере износа рабочих поверхностей

увеличиваются зазоры и уменьшается давление нагнетания, что ведет к росту

утечек РЖ, а, следовательно, к снижению эффективной мощности ГСТ-90 и, в

целом, производительности зерноуборочного комбайна.

Ресурс агрегатов гидропривода во многом определяется физико-

химическими свойствами РЖ [5]. Все гидроагрегаты ГСТ-90 периодически

работают в условиях неустановившихся режимов нагружения, при которых

возникает граничный режим смазки. Разрушение граничной смазочной пленки

имеет большое значение для практики, так как может привести к схватыванию,

заеданию и повышенному износу сопряженных деталей [3]. Отсюда вытекает

значение качества, как поверхностного слоя, так и применяемой РЖ, влияющих

на работоспособность элементов гидропривода.

115

Способность смазочной пленки РЖ разделять поверхности трения

определяется прочностью структурированного слоя поверхностно-активных

веществ, адсорбированных на поверхности, т.е. его несущей способностью [4].

В процессе эксплуатации гидропривода трансмиссии РЖ стареет [5]. В

результате этого происходит ухудшение ее эксплуатационных свойств, в том

числе уменьшение несущей способности смазочной пленки РЖ, которое

приводит к повышению износа поверхностей сопряжений ОГТ [6].

Цель исследований. Целью данной работы является оценка влияния

несущей способности смазочной пленки РЖ на скорость изменения объемного

КПД гидромотора ОГТ СХМ.

Результаты исследований. Наиболее дорогостоящими, а также

определяющими работоспособность гидромашинами на большинстве

современных СХМ с ОГТ, являются аксиальнопоршневые насосы и

гидромоторы. Наиболее широкое применение нашли аксиальнопоршневые

регулируемые насосы с наклонной шайбой марки НП 90 и

аксиальнопоршневые нерегулируемые гидромоторы с наклонной шайбой марки

МП 90, предназначенные для гидросистем с замкнутой цепью трансмиссий

типа ГСТ-90.

Аксиальнопоршневой нерегулируемый гидромотор МП 90 является

наиболее тяжелонагруженным агрегатом ОГТ в результате действия

неустановившихся внешних нагрузок и внутренних возмущений трансмиссии,

действующих на машину, поэтому рассматривался в качестве объекта

исследования.

В качестве исследуемой РЖ применялось гидравлическое масло МГЕ-

46В с различной наработкой. Отбор проб производился из системы привода

трансмиссии зерноуборочного комбайна Дон-1500. Свойства РЖ соответствуют

ТУ 38 001347-83. Предварительно определялась несущая способность

смазочной пленки РЖ по методике и устройстве, описанных в работах [7, 8].

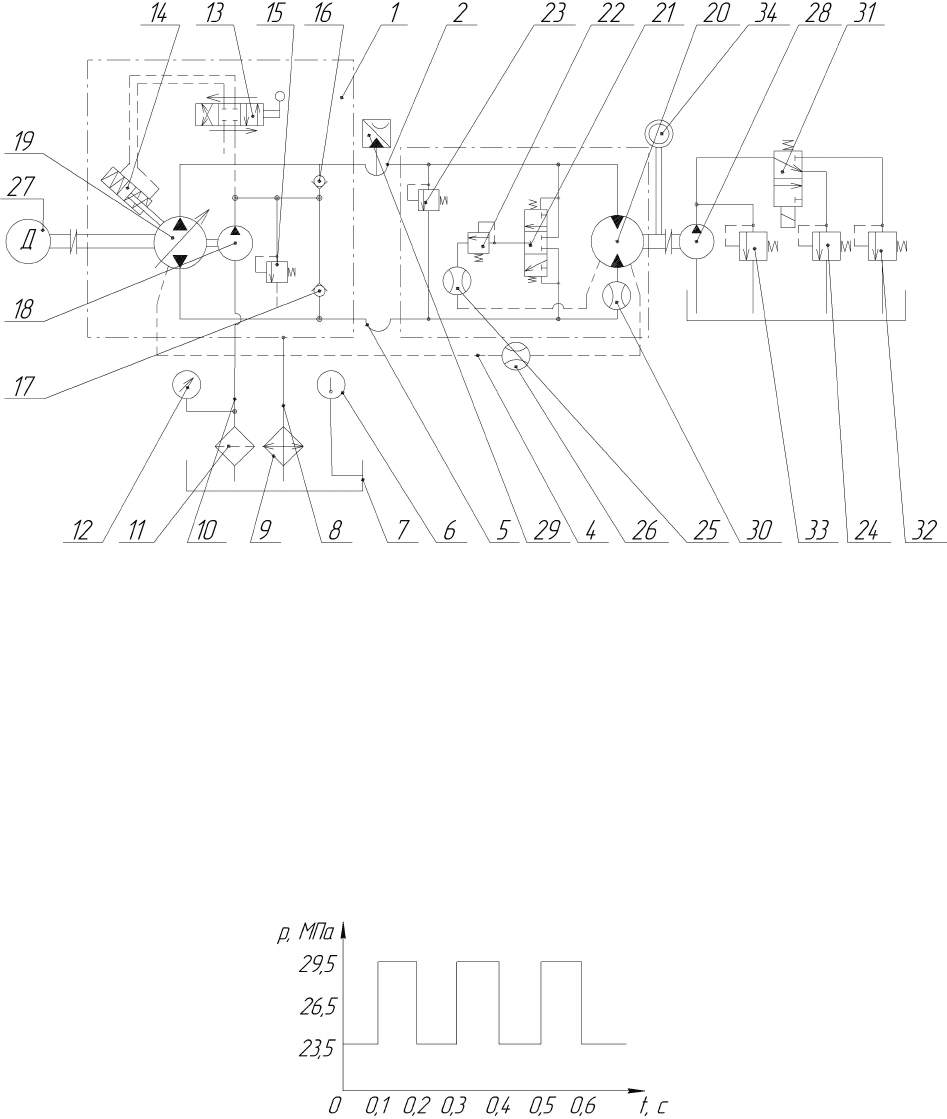
Схема стенда диагностики гидромотора МП-90 представлена на рис. 1.

Стенд работает следующим образом. Испытываемый гидромотор

монтируется согласно рис. 1. Прогревается РЖ до рабочей температуры,

(t=323 К); рычаг управления сервоцилиндра 4 устанавливается в крайнее

положение.

Давление в линии нагнетания 2 создается торможением выходного вала

гидромотора 20 нагрузочной станцией. Торможение осуществляется в

динамическом режиме, то есть вал гидромотора 20 вращается под заданной

нагрузкой. Циклограмма нагружения гидромотора на стенде показана на рис. 2.

Для автоматизации контроля параметров и управления в линию нагнетания 2

установлен датчик давления с аналоговым электрическим выходным

сигналом 29.

Температура РЖ контролируется термометром 6. В линию низкого

давления 5 встроен расходомер 30 (индикатор расхода ИРЭ-200). В линию

дренажа 4 встроен расходомер 26 (счетчик жидкости ШЖУ-40/0,6).

Параллельно заглушенному каналу клапана подпитки 22 – корпус гидромотора

20 подключался расходомер 25 (счетчик жидкости ШЖУ-40/1,6).

116

Экспериментальные исследования по влиянию несущей способности

смазочной пленки РЖ на скорость изменения объемного КПД гидромотора

ОГТ СХМ проводились при следующих условиях: температура РЖ, t = 323 К;

частота вращения приводного вала насоса, n=25 с-1 (1500 об/мин); наработка

РЖ варьировалась в пределах Т = 0..720 мото-ч с шагом 200 мото-ч; чистота

РЖ не ниже 10 класса по ГОСТ 17216-2001; время проведения опыта

принималось равным 40 часов; давление в линии нагнетания 26,5 МПа,

амплитуда колебания 6МПа, частота колебания 0,2 с (циклограмма на рис. 2).

Рис. 1 – Схема стенда диагностики гидромотора:

1 – насос; 2 –гидролиния нагнетания; 3 – гидромотор; 4 – линия дренажа; 5 – гидролиния

низкого давления ; 6 – указатель температуры; 7 – бак; 8 – сливная линия; 9 – масляный

радиатор; 10 – линия всасывания; 11 – фильтр; 12 – вакуумметр; 13 – распределитель

управления; 14 – сервоцилиндр; 15 – предохранительный клапан подпитки; 16, 17 – обратные

клапаны; 18 – аксиальноплунжерный насос; 19 – насос подпитки; 20 – аксиальноплунжерный

гидромотор; 21 – челночный золотник подпитки; 22 – клапан подпитки;

23, 24, 32, 33 – предохранительные клапаны; 25 – расходомер (счетчик жидкости

ШЖУ-40/1,6), 26 – расходомер (счетчик жидкости ШЖУ-40/0,6), 27 – электродвигатель;

28 – нагрузочный насос; 29 – датчик давления; 30 – расходомеры (индикатор расхода

ИРЭ-200); 31 – распределитель; 34 – датчик частоты вращения.

Рис. 2 – Циклограмма нагружения гидромотора на стенде диагностики.

117

Для проведения эксперимента использовались два новых гидромотора

МП-90, изготовленных по ТУ 3 Украины 5786106.010-93.

Объемный КПД гидромотора определяли по зависимости:

0 м

ом

В Д КЛ

V n

Q Q Q







 

, (1)

где:

– рабочий объем гидромотора;

– частота вращения выходного звена гидромотора;

– расход, измеренный расходомером 30 на выходе их гидромотора;

– утечки РЖ в дренажную линию;

КЛ

– утечки РЖ через клапан подпитки.

Скорость изменения объемного КПД гидромотора определяли по

формуле:

н к

ом ом

ом

оп

 





 , (2)

где:

ом



ом



– начальная и конечная величины объемного КПД гидромотора;

оп

– длительность одного опыта.

Результаты проведенного эксперимента по определению влияния

несущей способности смазочной пленки РЖ на скорость изменения объемного

КПД гидромотора ОГТ СХМ представлены в рис. 3.

Анализ эмпирической функции регрессии, представленной на рис. 3

показывает, что при уменьшении несущей способности смазочной пленки РЖ

наблюдается увеличение скорости изменения объемного КПД гидромотора

ОГТ СХМ. Данное обстоятельство свидетельствует об увеличении скорости

изнашивания поверхностей сопряжений гидромотора и, как следствие,

увеличение утечек РЖ.

Рис. 3 – Зависимость скорости изменения объемного КПД гидромотора от несущей

способности смазочной пленки РЖ.

-1

, c

ом



118

Вывод. Таким образом, уменьшение несущей способности смазочной

пленки РЖ в процессе эксплуатации СХМ определяет, при прочих равных

условиях, увеличение скорости изменения объемного КПД гидромотора ОГТ,

обусловленного повышенным износом поверхностей сопряжений. Из чего

следует, что для предотвращения повышенного износа поверхностей

сопряжений ОГТ в процессе эксплуатации СХМ необходимо применение РЖ,

несущая способность смазочной пленки которой не превышает предельно-

допустимого значения.

Список использованных источников

1. Гідропривід сільськогосподарської техніки: Навчальне видання / О.М.

Погорілець, М.С. Волинський, В.Д. Войтюк, С.І. Пастушенко; За ред.

О.М. Погорільця. – К.: Вища освіта, 2004. – 368 с: іл.

2. Кондаков Л.А. Рабочие жидкости и уплотнения гидравлических систем /

Кондаков Л.А. – М.: Машиностроение, 1982. – 216 с.

3. Надежность объёмных гидроприводов и их элементов / [Беленков Ю.А.,

Нейман В.Г., Селиванов М.П., Точилин Ю. В.]. – М.: Машиностроение,

1977. – 167 с.

4. Зерноуборочные комбайны «Дон» / Ю.А. Песков, И.К. Мещеряков, Ю.Н.

Ярмашев, А.Р. Распопов и др. – М.: Агропромиздат, 1986. – 333 с., ил.

5. Проников А.С. Параметрическая надежность машин / Проников А.С. –

М.: Изд-во МГТУ им. Н.Э.Баумана, 2002. – 560 с.

6. Лысиков Е.Н. Надмолекулярные структуры жидких смазочных сред и их

влияние на износ технических систем / Лысиков Е.Н., Косолапов В.Б.,

Воронин С.В. – Х.: ЭДЭНА, 2009. – 274 с.

7. Косолапов В.Б. Влияние несущей способности смазочной пленки рабочей

жидкости гидропривода на ее противоизносные свойства /

В.Б. Косолапов, С.В. Литовка // Промислова гідравлика і пневматика. –

Вінниця: ВДАУ, 2010. – № 2 (28). – С. 20–23.

8. Литовка С.В. Влияние эксплуатационных параметров рабочей жидкости

гидропривода на стойкость адсорбционной пленки к внешней нагрузке в

режиме граничного трения / С.В. Литовка // Проблеми трибології. – 2008.

– № 4 (59). – С. 22–25.

Анотація

ОЦІНКА ВПЛИВУ НЕСУЧОЇ ЗДАТНОСТІ МАСТИЛЬНОЇ ПЛІВКИ

РОБОЧОЇ РІДИНИ НА ВИХІДНІ ПАРАМЕТРИ ОБ'ЄМНОГО

ГІДРОПРИВОДУ ТРАНСМІСІЙ СІЛЬСЬКОГОСПОДАРСЬКИХ

МАШИН

Косолапов В., Літовка С.

Виконані експериментальні дослідження впливу несучої здатності

мастильної плівки робочої рідини на швидкість зміни об'ємного коефіцієнта

корисної дії гідромотора об'ємного гідроприводу трансмісії

119

сільськогосподарських машин. Показано, що зменшення несучої здатності

мастильної плівки робочої рідини в процесі експлуатації сільськогосподарських

машин визначає, за інших рівних умов, збільшення швидкості зміни об'ємного

коефіцієнта корисної дії гідромотора об'ємного гідроприводу трансмісії.

Abstract

ESTIMATION OF INFLUENCE OF LOAD CARRYING CAPACITY OF

LUBRICATING FILM OF WORKING LIQUID ON OUTPUT PARAMETERS

OF THE TRANSMISSION HYDRODRIVE OF AGRICULTURAL

MACHINES

V. Kosolapov, S. Litovka

Experimental researches of influence of load carrying capacity of lubricating

film of working liquid for speed of change of volume efficiency of the hydromotor of

the transmission hydrodrive of agricultural machines have been executed. It has been

shown that reduction of load carrying capacity of lubricating film of working liquid

while in service agricultural machines defines, with other things being equal,

increase of change rate of volume efficiency of the hydromotor of the transmission

hydrodrive.

УДК 621.873

ДИСКРЕТНИЙ МЕТОД СИНТЕЗУ ОПТИМАЛЬНИХ КЕРУВАНЬ

ТЕХНИЧНИМИ СИСТЕМАМИ

Ловейкін В.С., д.т.н, Ромасевич Ю.О., к.т.н.

Національний університет біоресурсів і природокористування України

Приведено метод синтезу оптимального керування, який дозволяє

враховувати обмеження накладені на керування та інші динамічні та

кінематичні параметри руху системи. Запропоновано ієрархічну структуру

роботи системи керування, яка реалізує оптимальне керування на практиці.

Постановка проблеми. Керування у складних технічних ситемах різної

фізичної природи має велике значення, оскільки до них ставляться вимоги

найбільш раціонального використання pecypcів, вибору найкращих

можливостей програм дій тощо. Це пов’язано з тим, що технічні системи

„працюють” з високими енергіями, значними швидкостями, швидкоплинними

процесами. Усе це визначає проблеми, які становлять предмет теорії

оптимального керування.

Аналіз досліджень та публікацій. Загальна постановка задачі

оптимального керування така: необхідно знайти оптимальне керування, яке

знаходиться у області допустимих керувань і яке переводить технічну систему з

одного стану у інший при екстремізації деякого критерію, який відображає

120

бажані або небажані показники роботи системи. В залежності від областей

початкового та кінцевого стану (у частинному випадку область може

перетворюватись на точку), виду оптимізаційних критеріїв (функціональний,

термінальний критерій), області допустимих керувань (відкрита, закрита)

задача оптимального керування отримує той чи інший сенс.

Існує декілька математичних методів розв’язування задач оптимального

керування: варіаційне числення [1], принцип максимуму [2], динамічне

програмування [3]. Два останні методи були розроблені у 50-х роках минулого

сторіччя у зв’язку з тим, що область допустимих керувань для більшості

технічних систем є замкнутою. Це обмеження не дає змогу використати

класичне варіаційне числення для розв’язування подібних задач.

Принцип максимуму дозволяє оптимати оптимальне керування у функції

часу. Таке керування прийнято називати П-керуванням [4]. За допомогою

динамічного програмування можна отримати С-керування [4], яке є функцією

часу та фазових координат технічної системи. Це є перевагою, оскільки на

систему у процесі її руху можуть справляти вплив стохастичні збурення. Крім

того, параметри системи не завжди вдається точно визначити. Все це впливає

на кінцевий стан системи та на величину оптимізаційного критерію. Однією з

властивостей С-керування є те, що воно автоматично „враховує” всі

стохастичні збурення та неточності моделі і завжди „веде” систему по

оптимальній траєкторії. Крім того, якщо відома математична модель технічної

системи, то з С-керування можна отримати П-керування (наприклад,

підставивши його у праву частину диференціального рівняння і розв’язавши це

рівняння).

Недоліком методу динамічного програмування є складність розрахунків

при синтезі оптимального керування [5]. Якщо область допустимих керувань є

замкненою, то визначити оптимальне керування за допомогою динамічного

програмування надзвичайно складно.

Постановка мети дослідження. Метою дослідження є виклад методики

синтезу оптимального дискретного керування за допомогою динамічного

програмування., а також виклад пропозицій щодо практичного використання

отриманого оптимального керування. Відповідно до мети ставляться такі

задачі: 1) викласти методику синтезу оптимального керування при якій би

враховувалось обмеження накладене на керування рухом технічної системи; 2)

привести алгоритм роботи програми, яка б дозволила реалізувати оптимальне

керування на практиці.

Виклад основного матеріалу.

1. Синтез оптимального керування

Нехай потрібно перевести систему з стану

у стан

(

- це вектор

початкових, а

- кінцевих фазових координат системи). Керування обмежене

деякою областю:





(



- це область допустимих керувань). На траєкторії

руху системи необхідно мінімізувати критерій dtuxI



 















)()(



(