Волков А.Ф., Лумпиева Т.П. Лабораторный практикум по физике

Подождите немного. Документ загружается.

Молекулярная физика Описания лабораторных работ

Лабораторная работа № 14

ОПРЕДЕЛЕНИЕ УДЕЛЬНОЙ ТЕПЛОТЫ ПЛАВЛЕНИЯ ОЛОВА

Цель работы: определить удельную теплоту плавления олова.

Приборы и принадлежности: фарфоровый тигель с оловом, трубчатая

печь, милливольтметр, хромель−алюмелевая термопара, секундомер.

Общие положения

При плавлении вещества поглощается количество теплоты Q пропорцио-

нальное массе металла m:

mQ , (1)

где − удельная теплота плавления (кристаллизации), т.е. количество тепло-

ты, которое необходимо сообщить 1 кг твердого вещества, взятого при темпе-

ратуре плавления, для перехода его в жидкое состояние.

Такое же количество теплоты выделяется при кристаллизации. Темпера-

тура жидкого металла при кристаллизации остается постоянной. Отсюда следу-

ет, что количество теплоты, выделяющееся в единицу времени при кристалли-

зации, должно быть равно количеству тепла, отдаваемому в окружающую среду

в единицу времени (скорости теплоотдачи). На этом и основан применяющийся

в данной работе метод определения величины

Количество теплоты, отдаваемой в окружающую среду, обозначим через

. Скорость теплоотдачи

τΔ

равна скорости выделения теплоты кристалли-

зации:

τ−τ

τΔ

, (2)

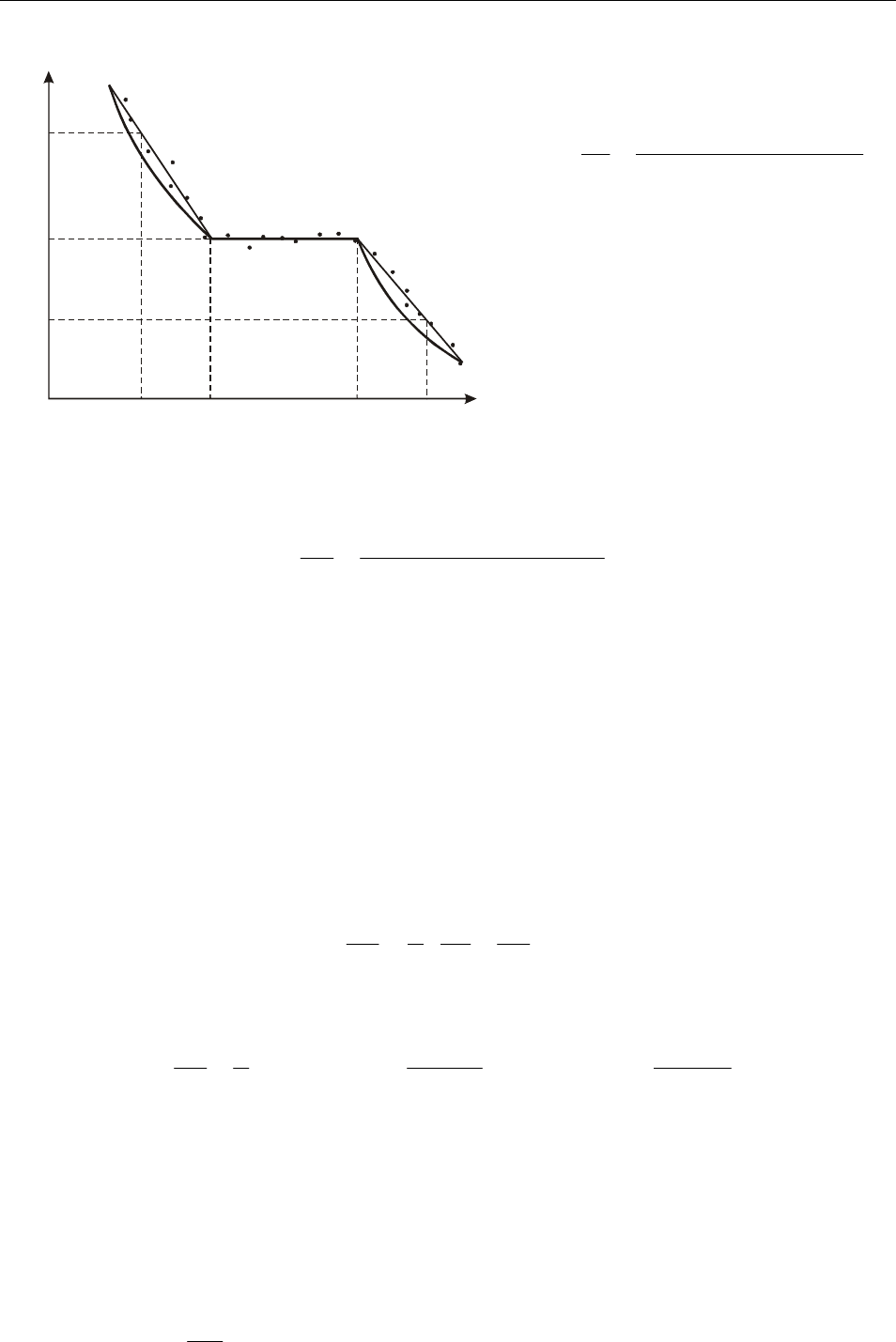
где − длительность процесса кристаллизации (рис. 1).

τ−τ

Отсюда:

()

τ−τ

τΔ

=λ

. (3)

Метод определения скорости теплоотдачи состоит в следующем. После

того, как металл в тигле расплавится и достигнет температуры, превышающей

на

температуру плавления, печь выключают и через равные промежут-

ки времени фиксируют показания милливольтметра. По градуировочному гра-

фику, приведенному на рис. 2, находят соответствующие этим показаниям зна-

чения температуры. Затем строят график зависимости температуры от времени,

примерный вид которого приведён на рис. 1.

3020 −

Участок АВ на графике соответствует остыванию жидкого металла до на-

чала кристаллизации, участок ВС − кристаллизации металла, а участок СД −

охлаждению твердого металла ( − температура плавления).

Заменим полученный график идеализированным, соединив точки А и В,

С и Д прямыми линиями.

Описания лабораторных работ Молекулярная физика

Количество теплоты, отдаваемой в среднем в единицу времени жидким

металлом вместе с тиглем при ос-

тывании:

(

)( )

21211

τ−τ

−⋅+

τΔ

TTmCMCQ

(4)

где M

− масса тигля;

m − масса металла;

− удельная теплоёмкость тигля

(С

=1090 Дж/кг⋅К);

− удельная теплоемкость иссле-

дуемого

жидкого металла

(для олова С

=266 Дж/кг⋅К).

При остывании твёрдого ме-

талла в единицу времени отдаётся

количество теплоты:

Рисунок 1

(

)

(

)

τ−τ

−⋅+

τΔ

TTmCMC

, (5)

где − удельная теплоемкость исследуемого твердого металла

( =230 Дж/кг⋅К).

Так как в процессе кристаллизации температура металла не изменяется,

то скорость теплоотдачи в этот период не может быть измерена непосредствен-

но. Скорость теплоотдачи при прочих равных условиях зависит от разности

температур между нагретым телом и окружающей средой, поэтому среднее

значение скорости охлаждения до наступления процесса кристаллизации и по-

сле него будет приблизительно равно скорости теплоотдачи в период затверде-

вания. Воспользовавшись этим, можно написать:

⎟

⎠

⎞

⎜

⎝

⎛

τΔ

, (6)

Используя уравнения (4), (5) и (6), находим:

()

(

)

⎥

⎦

⎤

⎢

⎣

⎡

τ−τ

−

τ−τ

−

τΔ

2`1

mCMC

. (7)

Моменты времени и на графике выбираются так, чтобы:

2334

2312

τ−τ=τ−τ

−

(8)

Подставим соотношение (7) в выражение (3). С учетом равенства (8), получим:

()()

(

)

()

[

]

2`12121

TTmCMCTTmCMC

−⋅++−⋅+=λ

. (9)

Молекулярная физика Описания лабораторных работ

Подготовка к работе

(ответы представить в письменном виде)

В чем состоит цель работы?

Какие физические величины измеряются непосредственно (прямые измере-

ния)?

Какой график надо построить по результатам эксперимента? Схематически

изобразите, какой вид должен иметь этот график по теории. Как на графике

выбираются моменты времени τ

и τ

Запишите формулу, по которой Вы будете рассчитывать удельную теплоту

плавления. Поясните смысл обозначений, входящих в формулу.

Запишите формулу, по которой Вы будете рассчитывать скорость теплоот-

дачи. Поясните смысл обозначений, входящих в формулу.

Выполнение работы

1. По термометру определить и записать значение комнатной температуры.

Записать в протокол массу тигля М и массу олова m, указанные на установке.

Определить цену деления милливольтметра

Опустить в трубчатую печь тигель с оловом.

Включить печь. Когда олово расплавится (показание милливольтметра дос-

тигнет величины 5 mV), выключить печь.

6. Поднять тигель и через 10 секунд записывать показания милливольтметра ε.

Измерения прекратить при достижении эдс 2,5 mV.

Оформление отчета

Расчеты

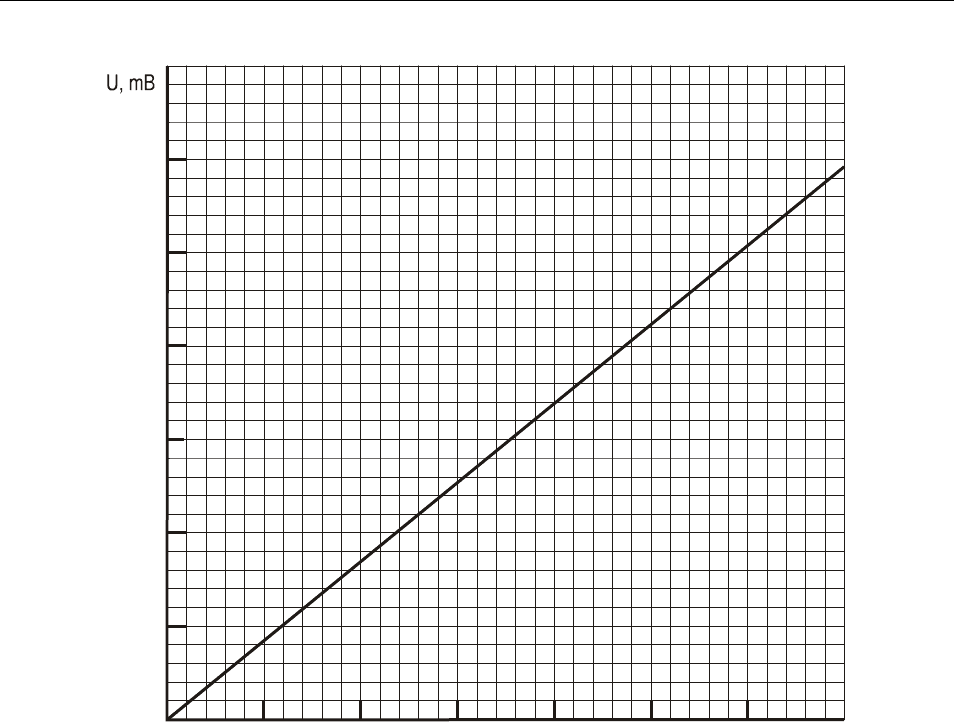
1. По градуировочному графику (см. рис. 2) определить разность температур

Δt, соответствующую каждому показанию милливольтметра.

Определить температуру олова для каждого момента времени по формуле

комн

ttT

где t

комн

– комнатная температура.

Построить график .

()

τ= fT

По графику определить температуру плавления .

Определить по графику температуры и . Для этого отложить от точек В

и С влево и вправо равные отрезки

−

(см. рис. 1).

Рассчитать удельную теплоту плавления олова по формуле (9).

Рассчитать скорость теплоотдачи по формуле (2).

Описания лабораторных работ Молекулярная физика

50 100

150 200

250

300

Δ°

, C

1,0

2,0

3,0

4,0

5,0

6,0

Рисунок 2

2. Защита работы

(ответы представить в письменном виде)

Дайте определение удельной теплоты плавления. От чего зависит ее значе-

ние?

Почему температура кристаллического тела во время плавления остается не-

изменной, несмотря на то, что к нему подводится теплота?

Каким агрегатным состояниям соответствуют участки АВ, ВС, СД на графи-

ке, приведенном на рис. 1?

4. Сравните полученный экспериментально график с теоретической зависимо-

стью. Сравните полученное значение удельной теплоты плавления олова с

табличным значением. Сделайте вывод.

Молекулярная физика Описания лабораторных работ

ПРОТОКОЛ

измерений к лабораторной работе №14

Выполнил(а)_____________________ Группа_________________

Комнатная температура t

комн

= ___________

Цена деления милливольтметра С

=___________

Масса тигля М = _________________

Масса олова m = ________________

Температура плавления Т

= __________

№

п/п

τ,

ε,

Δt,

°C

Дата________ Подпись преподавателя___________________

Описания лабораторных работ Молекулярная физика

Лабораторная работа № 15

ОПРЕДЕЛЕНИЕ ОТНОШЕНИЯ МОЛЯРНЫХ ТЕПЛОЕМКОСТЕЙ

ВОЗДУХА

Цель работы: определить отношение молярных теплоёмкостей воздуха

(показатель адиабаты).

Приборы и принадлежности: стеклянный баллон, U − образный мано-

метр, насос, секундомер.

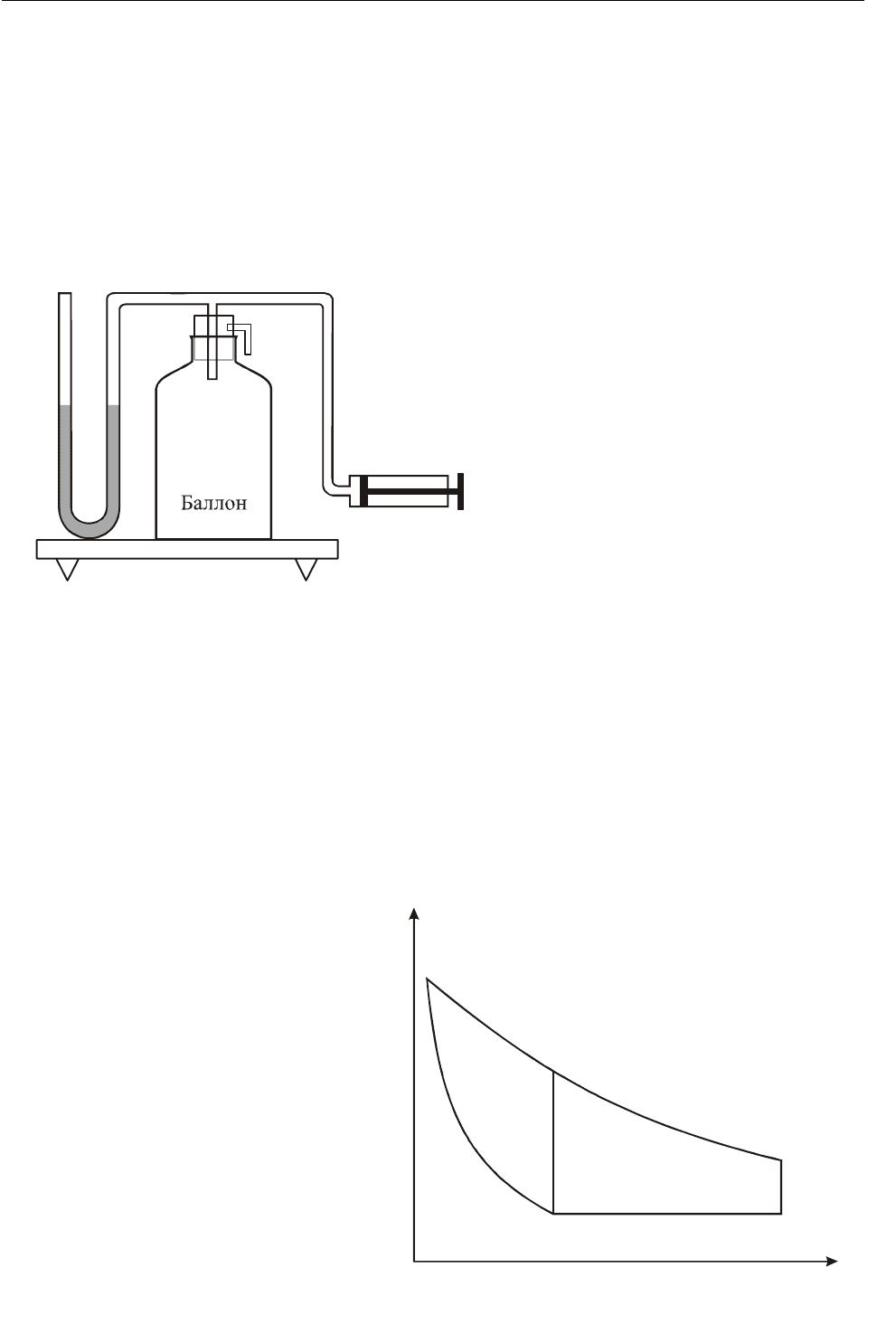
Описание экспериментальной

установки

Рисунок 1

Установка состоит из

стеклянного баллона, соеди-

ненного с открытым U–

образным манометром М и

насосом Н (рис. 1). Баллон за-

крыт пробкой, в которую

вставлен клапан К.

Общие положения

Адиабатический (адиабатный) процесс – это процесс, при котором физи-

ческая система не получает извне теплоты и не отдает ее. Адиабатные процессы

протекают в системах, окруженных теплоизолирующей (адиабатной) оболоч-

кой, но их можно реализовать и при отсутствии такой оболочки. Для этого про-

цесс должен протекать настолько быстро, чтобы за время его осуществления не

произошло теплообмена между системой и окружающей средой.

В баллон нагнетается воздух до определённой разности уровней жидко-

сти в коленах манометра. По

истечении 3-4 минут темпера-

тура воздуха в баллоне стано-

вится равной температуре ок-

ружающей среды. При этом

объем газа будет , давление

и температура (состоя-

ние 1 на рис. 2).

p V T

111

p V T

321

p V T

431

p V T

233

p V T

222

Рисунок 2

Затем на короткое время

открывается клапан К баллона

и воздух адиабатически пере-

ходит в состояние 2 (рис. 2).

Для адиабатного перехода из

первого состояния во второе

справедливо уравнение Пуас-

сона:

Молекулярная физика Описания лабораторных работ

VpVp

(1)

где − отношение молярной теплоемкости газа при постоянном давлении к

молярной теплоемкости при постоянном объеме. Этот коэффициент называют

показателем адиабаты.

При этом <0, т.к. работа расширения газа совершается за счет его

внутренней энергии.

TΔ

Через 3-4 минуты после закрытия клапана воздух нагревается изохорно

до комнатной температуры , причем давление повышается до величины

(состояние 3 на рис. 2). Сравнивая третье состояние газа с первым состояни-

ем, мы видим, что они принадлежат одной изотерме. По закону Бойля − Мари-

отта:

2311

VpVp

(2)

Из уравнений (1) и (2) можно определить . Для этого возводим уравне-

ние (2) в степень и делим его на уравнение (1):

γγ

Логарифмируя это выражение, находим :

(

)

()

=γ

(3)

Полученную формулу можно упростить. Обозначим разность уравнений

жидкости в манометре в первом состоянии через

Н, а в третьем через .

В этом случае:

023

hpp

Hpp

α+=

(4)

где − переводной коэффициент для перехода от разности к p. α hΔ

В каждом из этих выражений второе слагаемое в правой части мало по

сравнению с первым слагаемым. Из соотношения (4) получим:

()

013

hHpp

Hpp

−α−=

−

и подставим в формулу (3). Разделив числитель и знаменатель на , получим:

)(1

phH

−α−

α−

=γ

Величины

()

−α

много меньше единицы. Для малых значений

x справедливо приближенное выражение:

Описания лабораторных работ Молекулярная физика

(

)

−

1ln .

Применяя его, получаем:

()

−

=γ

. (5)

По этой формуле и производится вычисление . Величина , входящая в

формулу (5), получена в предположении, что клапан К закрывается в момент

окончания адиабатического процесса 1-2. Если клапан закрыть до или после за-

вершения процесса 1-2, то это приведет соответственно к завышению или за-

нижению величины

по сравнению с её действительным значением.

Для получения правильного результата измерений клапан необходимо за-

крыть в тот момент, когда газ находится в состоянии 2, что не представляется

возможным. Ввиду этого ординату 2-3, соответствующую разности уровней ,

приходится определять косвенным путем. Рассмотрим c этой целью процесс

адиабатического расширения при открытом клапане с учетом теплообмена с

окружающей средой во время протекания процесса 2-4 (рис.2).

Предположим, что газ находится в состоянии 1. Нажатием клапана К

произведем адиабатическое расширение (1-2). При этом температура газа пони-

зится относительно комнатной температуры до величины , давление ста-

нет равным атмосферному . Если

клапан оставить открытым в течение вре-

мени τ после окончания процесса 1-2, то температура газа в баллоне за это вре-

мя несколько повысится за счет теплообмена до величины

Т (изобарический

процесс 2-4). Закроем после этого клапан и оставим баллон на некоторое время,

пока температура внутри баллона не станет равной температуре окружающей

среды (изохорический процесс 4-5). При этом давление газа в сосуде повы-

сится на величину

Δ , которую определим по манометру по разности уровней

жидкости. С уменьшением времени τ величина

h , как это видно из рис. 3, воз-

растает и в пределе при стремится к искомому значению .

0→τ

Следовательно, величину

, можно определить, имея полученный на

опыте график зависимости от τ. Можно показать, что в условиях нашего

опыта имеет место соотношение:

hln

Рисунок 3

τ−

Ahh

lnln

т.е. наблюдается линейная зави-

симость от времени τ, при-

чем начальная ордината равна

логарифму искомой величины

. Здесь А есть угловой коэф-

фициент прямой, зависящей от

условий опыта.

hln

Получив на опыте ряд зна-

чений соответствующих раз-

личным длительностям расшире-

hln

Молекулярная физика Описания лабораторных работ

ния τ от одного и того же начального давления p, можно построить график за-

висимости

()

= fhln

, Зная, что график представляет собой линейную функ-

цию, можем экстраполировать его до пересечения с осью

ординат. Точка пере-

сечения графика с осью ординат соответствует (рис. 3).

ln h

Подготовка к работе

(ответы представить в письменном виде)

1. В чем состоит цель работы?

Какие физические величины измеряются непосредственно (прямые измере-

ния)?

Какой график необходимо построить по результатам эксперимента? Как при

помощи графика определить

По какой формуле Вы будете рассчитывать показатель адиабаты? Поясните

смысл обозначений, входящих в формулу.

Выполнение работы

1. Накачать в баллон воздух так, чтобы разность уровней жидкости в маномет-

ре стала равна 25-30 см. Оставить баллон на 3-4 минуты, пока температура

внутри его не станет равной температуре окружающей среды. После этого

отсчитать показания манометра и . Отчеты делать по нижнему краю

мениска.

Быстрым нажатием открыть клапан К и одновременно включить секундо-

мер. Выдержать клапан открытым 5 секунд и закрыть. Давление в баллоне

станет равным атмосферному (уровни жидкости сравнялись), а температура

понизится. Подождав 3-4 минуты, чтобы температура в баллоне повысилась

до комнатной (уровни жидкости разошлись), отсчитать показания манометра

и .

Повторить измерения согласно п.1-2, открывая клапан на 10, 15, 20, 25 и 30

секунд.

При этом начальный уровень жидкости в коленах манометра

каждый раз устанавливать на то же деление, что и в первом опыте

Оформление отчета

1. Расчеты

1. Рассчитать и h=

LLH −=

− .

Найти значения . hln

По полученным данным построить график

(

)

fhln

Найти значение , соответствующее τ = 0 (рис. 3), и определить .

Рассчитать показатель адиабаты по формуле (5).

ln h

2. Защита работы

(ответы представить в письменном виде)

1. Какой процесс называется адиабатическим (адиабатным)?

Запишите уравнение, описывающее адиабатный процесс (уравнение Пуассо-

на). Приведите схематичный график этого процесса.

Рассчитайте теоретическое значение показателя адиабаты воздуха и сравните

его со значением, найденным экспериментально. Сделайте вывод.

Описания лабораторных работ Молекулярная физика

ПРОТОКОЛ

измерений к лабораторной работе №15

Выполнил(а)_____________________ Группа__________________

№,

п/п

τ,

см

hln

1 5

2 10

3 15

4 20

5 25

6 30

ln h

= _____________

Дата________ Подпись преподавателя___________________