Витяев Е.Е. Извлечение знаний из данных. Компьютерное познание. Модели когнитивных процессов (2006)

Подождите немного. Документ загружается.

181

§ 73. Распознавание на основе комплексных сигналов

Процедура распознавания базируется на найденных комплексных сиг-

налах. Оценка позиций объекта получается на основании оценок всех оли-

гонуклеотидных сигналов, применимых к этой позиции. Эта оценка озна-

чает вероятность появления этого сигнала на случайной последовательно-

сти. Используя негативные случайные выборки, мы можем вычислить ве-

личину оценки, что гарантирует некоторый уровень ошибок первого

второго рода. Если в некоторой контрольной последовательности оценка

больше, чем эти уровни, тогда мы предсказываем, что эта последователь-

ность принадлежит некоторому функциональному классу.

На первом шаге процедуры распознавания мы находим, все сигналы

применимые к некоторой контрольной последовательности. В результате

мы имеем последовательность сигналов 0 < N < …<N

total

, где

total

– общее

количество сигналов. Порядок сигналов означает порядок появлений сиг-

налов в этой последовательности. Тогда может быть вычислена вероят-

ность P(S) появления этих сигналов для каждой позиции последовательно-

сти.

Вероятность P(S) для последовательности S = X

... X

получается

как произведение вероятностей нуклеотидов

, i = 1,2, ..., n.

P(S) =

∏

i 1

P(X

Функция распознавания базируется на некоторой последовательности

согласия

S, которая получается как показано на рис. 29.

Процедура распознавания, основанная на комплексных сигналах по-

добна процедуре, описанной выше. Мы определяем функцию распознава-

ния для анализируемой последовательности.

Вес последовательностей определяется несколькими способами:

1) ∑

log P(S) – сумма логарифмов условных вероятностей комплексных

сигналов, найденных в последовательности;

– число комплексных сигналов, найденных в последовательности;

3) ∑ logP(S

) – сумма вероятностей логарифмов олигонуклеотидных

сигналов, найденных в последовательности.

Базируясь на этих оценках последовательностей, мы разработали метод

прогнозирования донорных сайтов связывания. Полученные ошибки пер-

вого и второго рода на контрольных данных были 4,4 и 4,0 % соответст-

венно.

182

§ 74. Обсуждение

Разработанная система Gene Discovery помогает нам находить ком-

плексные сигналы в области промотера. Функциональное значение сигна-

ла можно рассматривать в терминах сайтов связывания транскрипционных

факторов или конформационных свойств ДНК.

Автоматическая генерация правил для функциональной аннотации ге-

нов может использовать и другие методы извлечения знаний. Для предска-

зания функционального класса генов мы планируем объединить результа-

ты других методов, дающих элементарные сигналы, которые могут быть

использованы системой

Gene Discovery для обнаружения комплексных

сигналов, связанных не только с сигналами контекста регулирующих об-

ластей.

Проведенный анализ дает большое число комплексных сигналов для

промотеров эндокринной системы и промотеров эритроид-специфичных

генов. Функциональное значение комплексных сигналов подтверждено

похожестью расположением олигонуклеотидных мотивов относительно

старта транскрипции и похожими расстояниями между этими мотивами.

Частным типом комплексных

сигналов являются, так называемые,

композиционные элементы [http://compel.bionet.nsc.ru/]. Композиционный

элемент формируется парой транскрипционных факторов, которые приоб-

ретают новые регулирующие свойства из-за взаимодействия белка с бел-

Рис. 29

183

ком. Такое взаимодействие обеспечивает большую экспрессию транскрип-

ции. Анализ закономерностей, найденных системой

Gene Discovery дает

новый подход для компьютерного обнаружения композиционных элемен-

тов.

Доступные экспериментальные данные и специализированные молеку-

лярно-биологические базы данных содержат большое количество экспе-

риментальных результатов для последовательностей ДНК, вовлеченных в

регулирование транскрипции. В настоящее время больше чем 300 молеку-

лярно-биологических баз данных доступны в Интернет, и это число про-

должает

расти. Это обеспечивает большие возможности для анализа дан-

ных и извлечения знаний в биоинформатике.

Наш подход мы применили в основном для анализа регуляторных рай-

онов генов. В дальнейшем мы предполагаем проанализировать контекст-

ную структуру генов для всех уровней генной иерархии: генов в целом,

регуляторных областей генов, промотеров, сайтов связывания транскрип-

ционных

факторов, 5'UTR, сайтов сплайсинга.

184

ГЛАВА 8. ЕСТЕСТВЕННЫЕ КЛАССИФИКАЦИИ

И ОНТОЛОГИИ КАК ЗАКОНЫ ПРИРОДЫ

§ 75. Что такое естественная классификация

Понятие естественной классификации, несмотря на его важность, до

сих пор не вошло в обиход современной науки. Понятие естественной

классификации развивалось в 1970–1980 гг. в рамках классификационного

движения. В рамках этого направления был систематизирован опыт есте-

ствоиспытателей по созданию естественных классификаций, организовано

несколько конференций и создана библиография. В данной работе, обоб-

щающей опыт

классификационного движения, предлагается формализация

понятия естественной классификации.

В рамках классификационного движения В. Ю. Забродин систематизи-

ровал критерии «естественности» классификации, которые в различное

время выдвигались естествоиспытателями [45; 62]. Приведем эти крите-

рии.

1. Смирнов Е. С. [77]: «Таксономическая проблема заключается в «ин-

дикации»: от бесконечно большого числа признаков нам нужно перейти к

ограниченному их количеству, которое заменило бы все остальные при-

знаки»;

2. Рутковский Л. [70]: «Чем в большем числе существенных признаков

сходны сравниваемые предметы, тем вероятнее их одинаковость и в дру-

гих отношениях»;

Уэвель В. [Там же]: «Чем больше общих утверждений об объектах

дает возможность сделать классификация, тем она естественней»;

4. Любищев А. А. [45]: «Наиболее совершенной системой является та-

кая, где все признаки объекта определяются положением его в системе.

Чем ближе система стоит к этому идеалу, тем она менее искусственна, и

естественной следует

называть такую, где количество свойств объекта, по-

ставленных в функциональную связь с его положением в системе, является

максимальным (в идеале это все его свойства)».

Участники классификационного движения по инициативе инициатора

движения Кожара В. Л. также дали некоторые определения естественной

классификации:

5. Забродин В. Ю. [45]: «Естественной» является та, и только та клас-

сификация, которая выражает закон природы»;

6. Шрейдер С. А. [86]: «В многообразии объектов, образующих «есте-

ственную» классификацию, можно обнаружить два типа закономерностей:

― соотношения, связывающие «короткое» описание архетипа, доста-

точное для диагностирования принадлежности объекта к данному классу, с

185

«полным» описанием. В сущности, это законы, позволяющие на основании

принадлежности объекта к некоторому естественному классу прогнозиро-

вать все его свойства;

― правила, показывающие как деформируются свойства объектов при

переходе к смежным классам. Именно они гарантируют возможность пе-

реноса знаний с одного объекта на все принадлежащие данному классу и,

несколько сложнее,

на объекты смежных классов»;

7. Витяев Е. Е. [14; 29; 34]: «Разбиение на классы должно производить-

ся так, чтобы объекты одного класса подчинялись одним и тем же законо-

мерностям. Между классами существуют закономерности перехода от

класса к классу. Объекты класса, кроме того, должны обладать некоторой

целостностью. Целостность – взаимная согласованность закономерностей

класса по взаимному предсказанию

свойств объектов».

Далее мы введем определение естественной классификации и система-

тики объясняющее перечисленные выше свойства естественной классифи-

кации.

§ 76. Онтологии и описание предметной области.

В последнее время внимание различных исследователей привлекают

онтологии. Это понятие заимствованно из философии. Точного определе-

ния этого понятия для задач искусственного интеллекта до сих пор нет.

Емкое определение онтологии дал Thomas R. Gruber [106] как специфика-

цию концептуализации. Неформально онтология представляет собой опи-

сание предметной области. Такое описание, обычно называемое концеп-

туализацией, состоит из системы

понятий и определений новых понятий,

описания предмета и методов исследования и априорного знания об объ-

ектах и методах исследования.

Построение онтологий предполагает концептуализацию предметной

области (ПрОбл), которая включает в себя систему понятий и величин, а

также систему законов аналитических и синтетических, связывающих ме-

жду собой понятия и величины. Понятие естественной

классификации

предполагает заданной некоторую онтологию. Приведем определение он-

тологии необходимое для введения понятия естественной классификации.

Онтология состоит из системы понятий ПрОбл, которая содержит:

– систему взаимосвязанных понятий, определяющих предмет рассмотре-

ния и цели исследования и что именно интересует нас в объектах

ПрОбл;

– потенциально бесконечное множество признаков, величин (оснований)

характеризующих объекты.

– систему законов ПрОбл, включающей:

аналитические выражения, фиксирующие связь понятий;

186

законы, например, физические, устанавливающие взаимосвязь ве-

личин; множество индуктивных законов (закономерностей), устанавли-

вающих взаимосвязи между потенциально бесконечным множеством при-

знаков, характеристик (оснований) объектов ПрОбл.

Аналитические выражения являются априорными. Индуктивные зави-

симости могут быть явно представлены в системе законов ПрОбл или мо-

гут быть обнаружены некоторым методом

Data Mining на множестве объ-

ектов ПрОбл. Аналитические выражения имеют статус определений и мо-

гут рассматриваться как аксиомы ПрОбл. Закономерности тоже могут

быть выражены в виде некоторых логических утверждений и имеют неко-

торую дополнительную характеристику своей выполнимости – вероятно-

сти, достоверности и т. д.

Объекты ПрОбл являются целостными образованьями, соединяющими

в себе понятия

из системы понятий и законы из системы законов ПрОбл.

Поэтому законы из системы законов выполнены (с некоторой степенью

вероятности, достоверности и т. д.) на объектах ПрОбл.

Если на систему законов ПрОбл смотреть как на систему аксиом

ПрОбл, сформулированную в системе понятий ПрОбл, которой должны

удовлетворять объекты ПрОбл, то объекты являются объектами

-моделями

системы аксиом ПрОбл. Совокупность всех таких объектов-моделей сис-

темы аксиом ПрОбл дает картину всех возможных объектов ПрОбл в дан-

ной системе понятий и позволяет предсказывать существование новых

объектов, удовлетворяющих системе аксиом ПрОбл.

§ 77. Формальное определение «естественной» классификации

и систематики

Определим модель M

объекта a. В нее входит множество Ω

значений

всех понятий, признаков, характеристик и величин, которые применимы к

объекту и принимают на нем определенные значения (истинности, число-

вые). Выделим из системы законов ПрОбл подмножество Z

, законов и за-

кономерностей, которые применимы к данному объекту. Это будут не все

закономерности системы законов ПрОбл. Например, закономерности вида

IF…THEN… не применимы к объекту, если посылка правила не выполне-

на на объекте. Подмножество Z

дает закономерную структуру объекта.

Модель M

= 〈Ω

, Z

〉 назовем закономерной моделью объекта.

Рассмотрим некоторый класс

ℭ объектов. Определим закономерную

модель класса

ℭ

= 〈Ω

ℭ

, Z

ℭ

〉 как пересечение всех закономерных моделей

объектов класса

ℭ.

Проанализируем критерий Е. С. Смирнова [77]. Разнообразие классов

всегда несопоставимо меньше разнообразия комбинаций значений призна-

187

ков и, следовательно, между значениями признаков должно существовать

огромное количество закономерных связей. Если число классов составля-

ет, например, сотни, а признаки бинарные, то независимыми среди них мо-

гут быть только около 10 признаков: 1024 = 2

. При классификации жи-

вотных, растений, почв и т. д. естествоиспытатели могут использовать ог-

ромное, потенциально бесконечное, множество признаков и характери-

стик. Но среди них только десяток признаков может быть в известной сте-

пени независим, а остальные признаки связаны между собой закономерно-

стями так, что из десятка признаков предсказываются значения всех

ос-

тальных признаков. Найти признаки, из которых предсказываются все ос-

тальные и составляет проблему индикации. Такими значениями признаков

в закономерной модели класса M

ℭ

являются порождающие совокупности

значений признаков. По набору значений порождающих признаков

〈x

= x

i1j1

, x

= x

i2j2

, …, x

= x

imjm

〉, где x

i1j1

, x

i2j2

, …, x

imjm

– значения при-

знаков x

i1j1

, x

, …, x

, и закономерностям из Z

ℭ

мы можем предсказать все

остальные значения признаков Ω

ℭ

объектов класса. Понятно, что набор

значений порождающих признаков определяется неоднозначно.

Предположим, что все классы {

ℭ

∈

} нам известны и мы знаем все зако-

номерные модели этих классов M

ℭi

. Рассмотрим задачу построения систе-

матики. Будем искать такие порождающие наборы признаков x

, x

, …,

, что для каждого класса из {ℭ

∈

} набор значений признаков

〈x

= x

i1j1

, x

= x

i2j2

, …, x

= x

iNjN

〉 является порождающим. Набор призна-

ков S = 〈x

, x

, …, x

〉 будем называть системообразующим, если для

каждого класса из {

ℭ

∈

} значения порождающего набора признаков

〈x

= x

, x

= x

, …, x

= x

〉 различны. В этом случае каждый класс

будет однозначно определяться набором значений системообразующих

признаков. Понятно, что наборы системообразующих признаков также оп-

ределяются неоднозначно. Задача и состоит в том, что бы найти наиболее

компактный и информативный набор системообразующих признаков. В

работах [8; 48; 163] также ставиться задача нахождения минимального

множества «существенных» признаков.

Систематика состоит в

том, чтобы представить некоторым образом, на-

пример таблицей, как изменяются наборы значений системообразующих

признаков при переходе от объектов одного класса к объектам другого

класса. Значения остальных признаков объектов класса будут предсказы-

ваться по значениям системообразующих признаков данного класса. Из-

менение значений системообразующих признаков может удовлетворять

некоторому закону, вследствие чего систематику

можно представить неко-

188

торым специальным образом, чтобы этот закон был виден наглядно. Опре-

делим

закономерную модель систематики как M

= 〈S, Z

〉, где S – набор

системообразующих признаков, а Z

– закон систематики – закон изме-

нения значений признаков из S при переходе от класса к классу. Каждому

набору значений системообразующих признаков S соответствует некото-

рый класс M

ℭ

= 〈Ω

ℭ

, Z

ℭ

〉. Тогда закон систематики Z

является метазако-

ном по отношению к закономерностям класса Z

ℭ

. Закон систематики Z

связан с законами классов как это определено в определении данном

С. А. Шрейдером [86]. Закономерностями первого типа являются законо-

мерности соответствующего класса Z

ℭ

, а закономерностями второго типа

– закон систематики Z

Рассмотрим критерий А. А.Любищева [45]. Системой по Любищеву яв-

ляется такое представление классификации объектов, где по месту объекта

в системе определяются все его признаки. В нашем определении значения

признаков некоторого объекта определяются взаимодействием двух зако-

нов – сначала

законом систематики Z

, используя который, мы по положе-

нию объекта в системе

можем определить значения системообразующих

признаков и

класс, к которому принадлежит этот объект, и далее по значе-

ниям системообразующих признаков этого класса и по закономерностям

класса

ℭ

мы можем определить все остальные свойства объекта.

Определим систематику как набор Σ = 〈S, Z

, {Z

ℭi

}

∈

〉. Не все законо-

мерности из системы законов ПрОбл будут входить во множества законо-

мерностей Z

, {Z

ℭi

}

∈

, так как эти множества зависят от выбора порож-

дающих признаков. Задача и состоит в том, чтобы выбрать наиболее со-

вершенную систему объясняющую свойства и строение объектов про-

стейшим образом. Систематика как закон природы определяется набором

〈S, Z

, {Z

ℭi

}

∈

〉.

Предположим теперь, что нам неизвестно разбиение объектов на клас-

сы. Тогда систематику надо строить по закономерным моделям объектов, а

не классов. Задача построения систематики сводится в этом случае к на-

хождению такого разбиения множества объектов на классы, чтобы постро-

енная на этих классах систематика была наиболее совершенной и простой.

189

§ 78. Пример построения систематики.

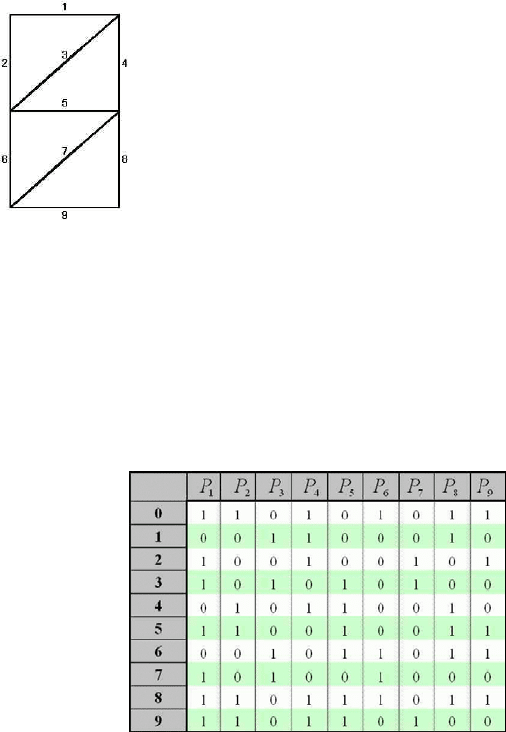
Рассмотрим цифры индекса как набор из десяти объектов. Предикат

P оз-

начает наличие i-го элемента в начертании цифры. Занумеруем признаки

таким образом как показано на рис. 30 Представление цифр признаками

показано на рис. 31.

Будем рассматривать цифры как классы {

ℭ

∈

{

}

0,..,9=I . Найдем закономерные модели этих классов.

Для этого будем искать закономерности в виде им-

пликативных детерминированных закономерностей, оп-

ределение которых приведено ниже.

Рассмотрим М = {A, Q} – модель сигнатуры Ω =

, …, P

}, где A – генеральная совокупность объектов;

Q = {

P ,…,

P } множество предикатов сигнатуры Ω, за-

данных на А; P

, i = 1, …, 9 – предикатные символы сиг-

натуры Ω.

Импликативной детерминированной закономерно-

стью назовем истинную на A формулу вида

F = (P

ε1

(a)& … &P

εm

(a) ⇒ P

ε0

(a)),

где {P

, …, P

, P

} ⊂ {P

, …, P

}, ε = 1(0), если отношение берется без от-

рицания (с отрицанием), удовлетворяющую следующим условиям:

― среди атомарных отношений P

ε1

(a), … , P

εm

(a), P

ε0

(a) нет повто-

рений и нет одновременно отношения и его отрицания;

― если из конъюнкции P

ε1

(a)& … &P

εm

(a) удалить одно из отноше-

ний, либо заменить отношение P

ε0

(a) на 0 (ложь), то полученная формула

Рис. 30

Рис. 31

190

станет ложной на A.

Найдем все импликативные детерминированные закономерности для

системы законов предметной области

{

}

0,..,9=I . Получим 3 743 законо-

мерности, найденные программой в таблице 1.

Далее для каждого класса выделим закономерности, которые на нем

выполняются. Например, для цифры 2 будет выполнено 529 закономерно-

стей.

По таблице (набор значений признаков) и набору закономерностей

можно получить закономерную модель класса. Выделим для каждого

класса минимальные определяющие совокупности.

Для двойки это будет, например, совокупность

{

}

P,P . Значения ос-

тальных признаков восстанавливается по следующим закономерностям:

¬P

&¬P

⇒ P

¬P

&¬P

⇒ P

&¬P

⇒ ¬P

¬P

&¬P

⇒ ¬P

¬P

&¬P

⇒ P

&¬P

⇒ ¬P

&¬P

⇒ P

Как уже упоминалось, определяющие совокупности выделяются не

единственным образом. Например,

{

}

P,P

тоже будет определяющей со-

вокупностью, для которой значения остальных признаков восстанавлива-

ется по следующим закономерностям:

⇒ P

&¬P

⇒¬P

&¬P

⇒ P

&¬P

& P

⇒¬P

¬P

&¬P

⇒P

&¬P

⇒¬P

&¬P

& P

⇒ ¬P

Глядя на закономерности видно, что в порождающих

{

}

P,P законо-

мерная модель двойки проще. Она будет выглядеть следующим образом:

= 〈Ω

, Z

〉 = {{1, 0, 0, 1, 0, 0, 1, 0, 1}, {P

, ¬P

, P

⇒ P

, P

&¬P

⇒¬P

&¬P

⇒ P

, P

&¬P

& P

⇒¬P

, ¬P

&¬P

⇒P

, P

&¬P

⇒¬P

&¬P

⇒ ¬P

}}. По минимальной определяющей совокупности каж-

дой цифры мы можем построить ее закономерную модель.