Вайнштейн Р.А., Коломиец Н.В., Шестакова В.В. Режимы заземления нейтрали в электрических системах
Подождите немного. Документ загружается.

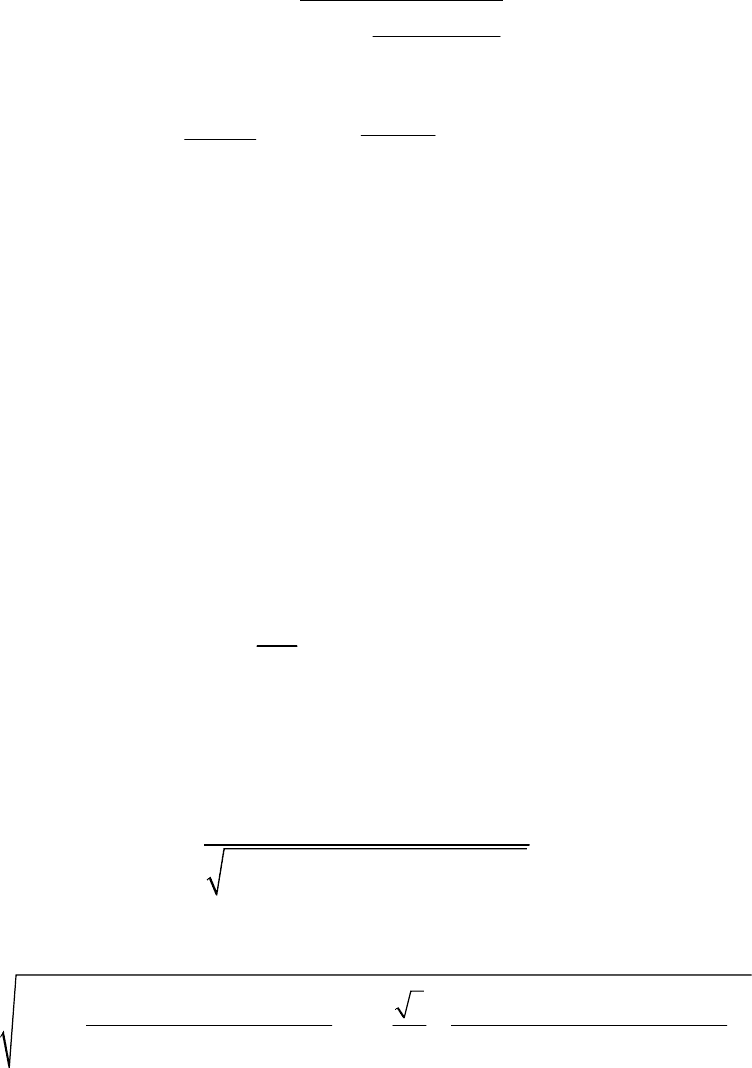
Приняв, как и ранее в качестве базисной суммарную емкостную
проводимость фаз сети относительно земли (3ω ) преобразуем (5.6)
следующим образом
Ф
C
П
З C
N
1
II
1
R
dG j
∗
∗
=
+
+
+
, (5.7)
где ,
ППФ
RR3C
∗
=ω
Ф
Ф
3G
d
3C
=
ω
,
N
N
Ф
G
G
3C
∗
=
ω
,
– емкостная составляющая тока замыкания на зем-
лю.
CA Ф
IE3jC=ω
Приняв в (5.7) , получим
П
R
∗
= 0
C
З aaN
III I
=
++
, (5.8)
где – активная составляющая тока замыкания, обусловленная
активной проводимостью фаз сети относительно земли,
aC
II=
d
aN Ф NCN
IEGIG
∗
==
– активная составляющая тока замыкания, обуслов-
ленная заземлением нейтрали через резистор.
Очевидно, что относительная проводимость
N
G
∗
равна также от-
ношению дополнительного активного тока к емкостному току замыка-
ния, которое обозначим
aN
aN
C
I
I
I
∗
=
.
Действуя также, как и при выводе соотношений (4.20) и (4.22), по-
лучим для абсолютных значений:
напряжение на нейтрали
()
П N П
Ф
N
2
2
П
E
U
dR G R 1 R
∗∗∗
∗
=
+++
; (5.9)
напряжения на неповрежденных фазах
()
()
()
П N П
П
П N ППN ПП
22
C,B Ф
22
dR G R 1
3R
UE0,5
2
dR G R 1 1 dR G R 1 R
∗∗∗
∗
∗∗∗ ∗∗∗ ∗
⎛⎞⎛
++
=+ +±
⎜⎟⎜
⎜⎟⎜
+++ +++
⎝⎠⎝
⎞
⎟
⎟
⎠
(5.10)
92
ЭЛТИ ТПУ
В (5.10) знак «+» относится к фазе опережающей по отношению к
поврежденной, а «–» к отстающей.
На рис. 5.4 построены графики напряжений на нейтрали и непо-
врежденных фазах в зависимости от переходного сопротивления при
различных значениях .
N
G
∗
П*
R
1
U
*
0246810
0.5
1
1.5
2
.
.
o.e
.
o.e
.
2
3
4
5
6
Рис. 5.4. Графики напряжений в зависимости от переходного сопротивления
1, 2 – напряжение на нейтрали;
3,4 – напряжение на фазе С;
5,6 – напряжение на фазе В;
1, 3, 5 – построены при
N
G1
∗
=
;
2, 4, 6 – построены при
N
G0,
∗
5
=
Как и следовало ожидать, при
П
R
∗
0
=
и при любом значении
N
G
∗
напряжения на неповрежденных фазах равно линейному и, для приня-
тых значений
N
G
∗
, сопротивления прямой и обратной последовательно-
стей значительно меньше сопротивления нулевой последовательности.
Также вполне объяснимо и то, что при одних и тех же значениях пере-
ходного сопротивления напряжение нулевой последовательности
меньше, чем в сети с изолированной нейтралью и в сети с компенсацией
емкостного тока.
Напряжение смещения нейтрали, вызванное емкостной несиммет-
рией, при отсутствии замыкания определяется также как и в сети с изо-
лированной нейтралью (4.24) при
LN
GG
=
()
N
C
Nсм Ф
2
UE
dG 1
∗
α
=
+
+
. (5.11)
93
ЭЛТИ ТПУ
Из (5.11) следует, что при резистивном заземлении напряжение
смещения нейтрали при прочих равных условиях (при определенной
емкостной несимметрии) тем меньше, чем больше .
N
G
5.2. Влияние резистивного заземления нейтрали на
перенапряжения при повторных зажиганиях дуги
Переходные процессы в сети с резистивным заземлением нейтрали
будем рассматривать по схеме замещения, приведенной на рис. 5.2.
Заземляющий резистор в принципе оказывает влияние на переход-
ный процесс после погасания дуги. При рассмотрении переходных про-
цессов, вызываемых пробоем изоляции одной из фаз, в сети с компенса-
цией емкостного тока было принято, что дугогасящий реактор не ока-
зывает на эти процессы практически никакого влияния, так как его со-
противление при высоких частотах переходных процессов весьма вели-
ко. При заземлении нейтрали через резистор отсутствие такого влияния
не очевидно.
Рассмотрим сначала влияние заземляющего резистора на переход-
ные процессы изменения заряда емкостей неповрежденных фаз. При
оценке этого влияния пренебрежем индуктивностью заземляющего
трансформатора, что заведомо даст большее влияние, так как упомяну-
тые процессы носят высокочастотный характер.
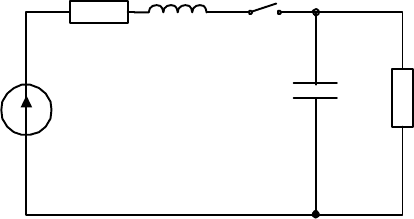
Полученные в главе 2 соотношения показывают, что переходный
процесс в неповрежденных фазах одинаков и проходит синхронно. По-
этому схема замещения, отображающая этот процесс представлена на
рис. 5.5, где – напряжение, при котором зажигается дуга (напряже-
ние пробоя).
пр
U
U
пр
N
G
Ф
2C
экв
L
экв
R
K
Рис. 5.5. Схема замещения контуров неповрежденных фаз для переходного
процесса при зажигании дуги
94
ЭЛТИ ТПУ

Дифференциальное уравнение, описывающее свободную состав-
ляющую переходного процесса в схеме (рис. 5.5), относительно напря-
жения на емкости
2
CNэкв CNэкв
C
2
Ф экв экв Ф экв Ф
du G R du G R
1
++ + + u=
dt 2C L dt 2L C 2L C
⎛⎞⎛ ⎞
⎜⎟⎜ ⎟
⎝⎠⎝ ⎠
0.
(5.12)
Коэффициенты дифференциального уравнения (5.12)
N экв
1
Фэкв
GR
д +
4C 2L
⎛⎞
=
⎜⎟
⎝⎠
,
2
N экв
p1
эквФ эквФ
GR
1
щ +
2L C 2L C
⎛⎞
=
⎜
⎝⎠
⎟
являются соответст-
венно коэффициентом затухания и квадратом резонансной частоты эк-
вивалентного контура переходного емкостного тока, которые с учетом
того, что представим в следующем виде
NN* Ф
G= G 3щC
/
11 N
3
дд+ щG
4
=
*
, (5.13)
2/2 /
p
1p1 1 N
щ =щ +3дщG
*
, (5.14)
где
//2
экв
1p1
экв экв Ф
R
1
д =,щ =
2L 2L C
– соответственно коэффициент затухания
и резонансная частота контура переходного емкостного тока без учета
влияния заземляющего резистора (в сети с изолированной нейтралью).
Таким образом, в сети с резистивным заземлением нейтрали коэф-
фициент затухания переходного емкостного тока замыкания определя-
ется по (5.13), а частота свободных колебаний равна
2
1p1
щ = щ - д
2
1
p1
0
p1
. (5.15)
Как видно из (5.13), (5.14), степень влияния проводимости зазем-
ляющего резистора на значения зависит от их исходных значе-
ний при . Для количественной оценки этого влияния примем
конкретные значения 1/с (2000 Гц) в соответствии
с принимаемым при расчете перенапряжений значением (3.13).
1
д , щ
N
G
∗
=
/
1p1
д = 420, щ 12566=
д1
k=0,1
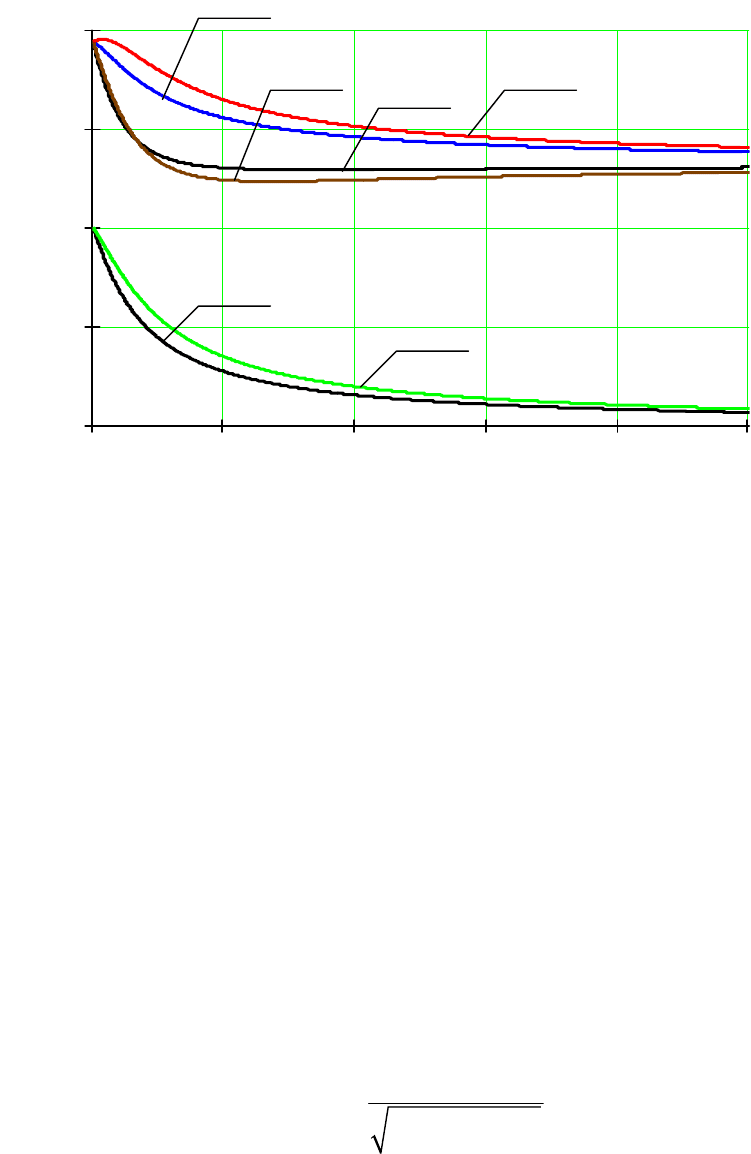
Зависимости от
1
д , щ
N
G
∗
приведены на рис. 5.6.
95
ЭЛТИ ТПУ
р11
ω , δ
1
с
p1 N
(G )
∗
ω
N*
G
1N
(G )
∗
δ
0 0.6 1.2 1.8 2.4 3
3500
7000
1.05
.
10
4
1.4
.
10
4
.
о.е.
Рис. 5.6. Зависимости коэффициента затухания и резонансной частоты
от проводимости заземляющего резистора
Как видно, даже при сравнительно больших значениях пере-
ходный процесс, вызванный зажиганием дуги, остается колебательным
слабозатухающим. Поэтому и в сети с резистивным заземлением ней-
трали погасание дуги может происходить при прохождении через нуль
суммарного тока замыкания, то есть практически через целое число по-
лупериодов составляющей с частотой
N
G
∗
1
ω
или при прохождении через
нуль принужденной составляющей тока.
Так как остаточное напряжение на нейтрали, обусловленное этими
зарядами, является одной из основных причин возникновения больших
перенапряжений, то определим значение
N
G
∗
, при котором выполняется
условие практически полного стекания избыточных зарядов за полови-
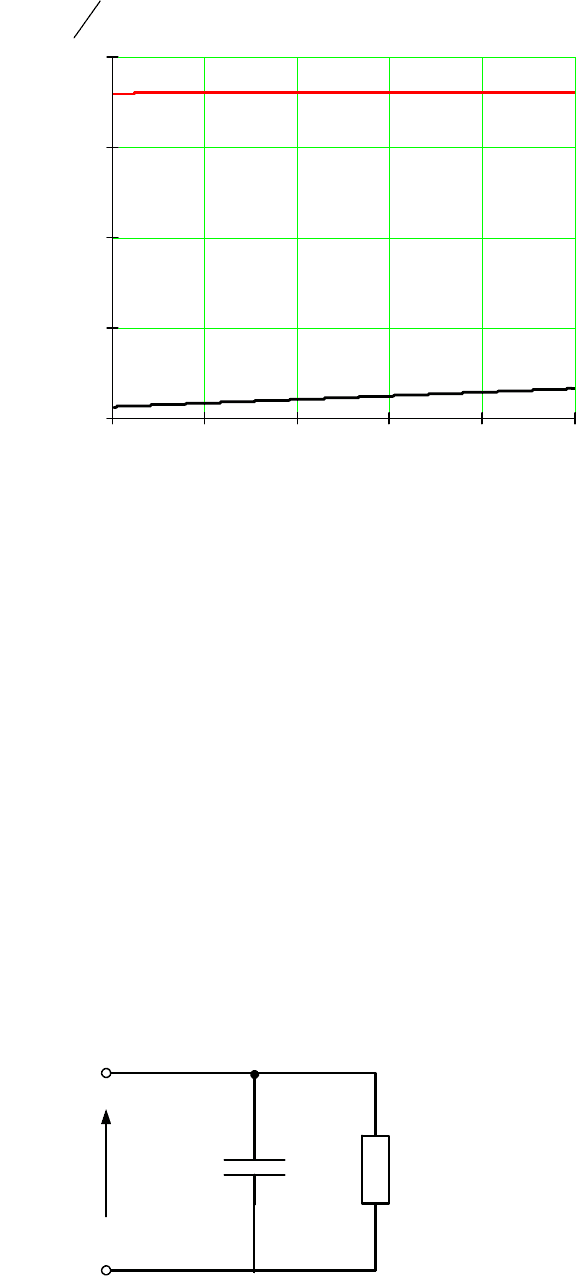
ну периода промышленной частоты после погасания дуги. Cхема заме-
щения нулевой последовательности для этой стадии процесса представ-
лена на рис. 5.7.
Ф N
3G G
+
N
u
Ф
j
3Cω
Рис. 5.7. Схема замещения сети с резистивным заземлением нейтрали
после погасания дуги
96
ЭЛТИ ТПУ
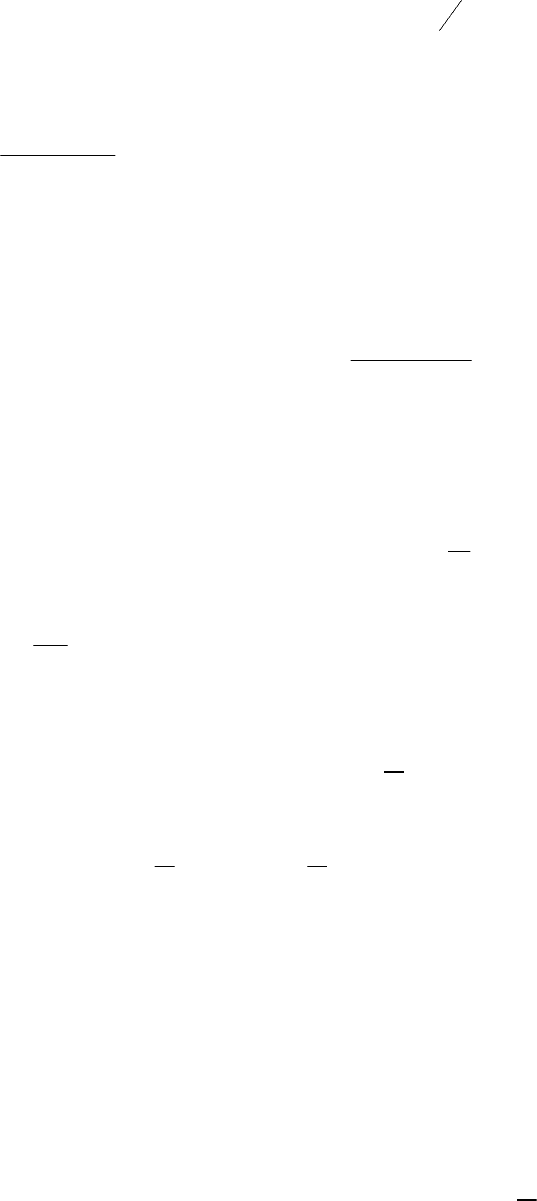
Напряжение на нейтрали после погасания дуги изменяется по зако-
ну
N
t
-
ф
NN0
uue=
, (5.16)
где – напряжение на нейтрали в момент погасания дуги,
N0
u
Ф
N
Ф N
3C
=
3G +G
τ
– постоянная времени процесса стекания избыточных за-
рядов.
Умножив и разделив выражение для
N
τ
на промышленную частоту
ω, приведем его к виду
N
N*
1
ф =
(d+G )щ
. (5.17)
Так как переходный процесс по (5.16) практически заканчивается
за время, равное , искомое значение
N
3τ
N
G
∗
найдем из условия
N
T
3ф =
2
, (5.18)
где
2р
T=
щ
– период напряжения промышленной частоты.
Подставив в (5.17) выражение (5.18) получим
N*
3
G=- d
р
.
Так как
3
d<<
р
, то
N*
3
G0,
р
≈=955
.
Таким образом, положительное влияние резистивного заземления,
проявляющееся в устранении эффекта накопления избыточных зарядов
при повторных зажиганиях дуги, практически полностью реализуется,
если дополнительная активная составляющая тока замыкания примерно
равна емкостной составляющей.
Так как стоимость заземляющего резистора при прочих равных ус-
ловиях уменьшается при уменьшении тока, на который он рассчитыва-
ется, то целесообразно рассмотреть насколько сохраняется эффект сни-
жения перенапряжений, если принимать
N*
3
G
р
<
.
97
ЭЛТИ ТПУ

Так как в принимаемом диапазоне значений
N
G
∗
(примерно от 0 до
1) переходный ток в месте замыкания может оставаться колебательным
со сравнительно слабым затуханием, то и в сети с резистивным зазем-
лением нейтрали формирование перенапряжений может происходить по
любой из известных теорий (пункт 3.3).
Проанализируем, как изменяются расчетные перенапряжения по
теории Петерсена при изменении
N
G
∗
. Для этого, очевидно, следует в
выражение для напряжения на нейтрали, формирующегося при очеред-
ном цикле зажигания и погасания дуги, ввести множитель, учитываю-
щий его затухание за половину периода промышленной частоты. В ре-
зультате получим
N
*
-
р
(d+G )
Nn BM(n-1)
2
u=u e
3
. (5.19)
При этом максимальное расчетное перенапряжение будет равно
N
C1
BMn Фm
(d G )
C1
1,5(1k)(1k)
uE
2
1(1k)(1k)e
3
∗
δ
−π +
δ
+
−−
=
−− −
. (5.20)
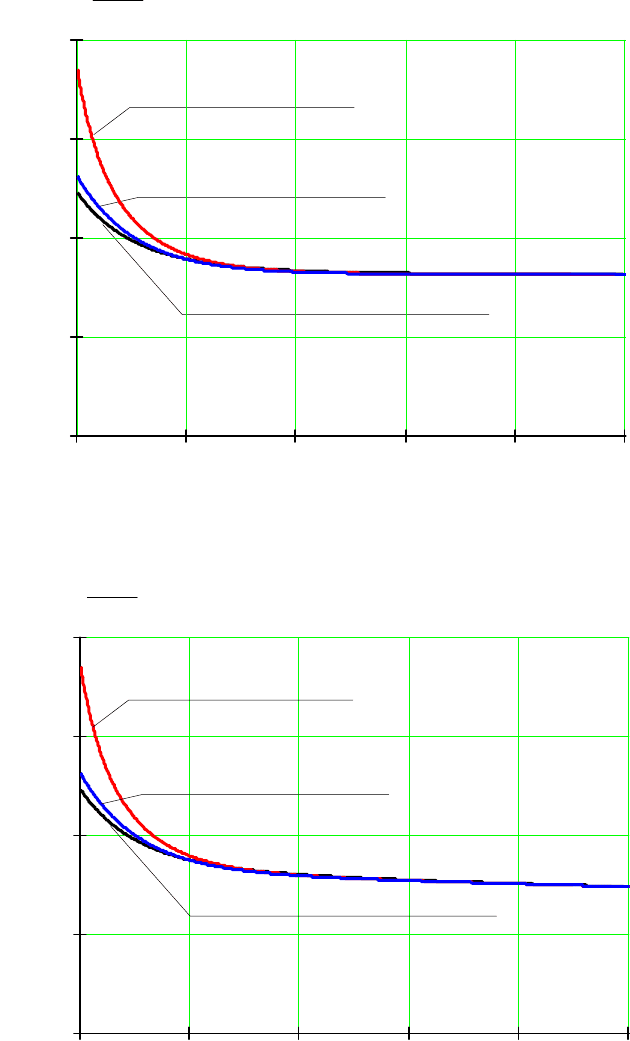
Зависимость перенапряжений от
N
G
∗
по (5.20) приведена на рис.
5.8. При расчете перенапряжений было учтено некоторое увеличение
затухания напряжения с частотой
1
ω
в соответствии с (5.13), поэтому
принято конкретное значение
1
420
δ
=
(1/с).
Влияние заземления через резистор на формирование перенапря-
жений по теории Петерса и Слепяна обусловлено не только затуханием
напряжения на нейтрали к моменту очередного зажигания дуги, но и
тем, что момент перехода принужденного тока замыкания через нуль
сдвигается относительно максимума напряжения на нейтрали. Поэтому
в момент погасания дуги начальное значение остающегося напряжения
на нейтрали меньше амплитуды фазного напряжения и, следовательно,
время от момента погасания дуги до достижения ближайшего максиму-
ма напряжения на поврежденной фазе меньше половины периода (рис.
5.9).
При погасании дуги в момент , когда полностью затухает пере-
ходный процесс, вызванный предыдущим зажиганием дуги, напряжение
на нейтрали (рис. 5.9) равно
2
t
98
ЭЛТИ ТПУ
BM
Фm
u
E
N*
G
теория Петерсена
теория Петерса и Слепяна
теория Белякова
o.e.
o.e.
0 0.6 1.2 1.8 2.4 3
1
1.75
2.5
3.25
4
.
а)
00.61.21.82.4 3
1
1.75
2.5
3.25
4
.
BM
Фm
u
E
теория Петерсена
теория Петерса и Слепяна
теория Белякова
o.e.
o.e.
N*
G
б)
Рис. 5.8. Зависимости перенапряжений от проводимости заземляющего резистора
а – без учета влияния резистора на коэффициент затухания;
б – с учетом влияния резистора на коэффициент затухания
99
ЭЛТИ ТПУ
o.e
.
N
u
0 0.006 0.012 0.018 0.024 0.03
1.5
1
0.5
0.5
1
1.5
..
0 0.006 0.012 0.018 0.024 0.03
35
24
13
2
9
20
..
A
e
1
t
2
t
3
t
t
t
c
c
2
t
Cm
i
I
3
β
Фm
u
E
o.e.
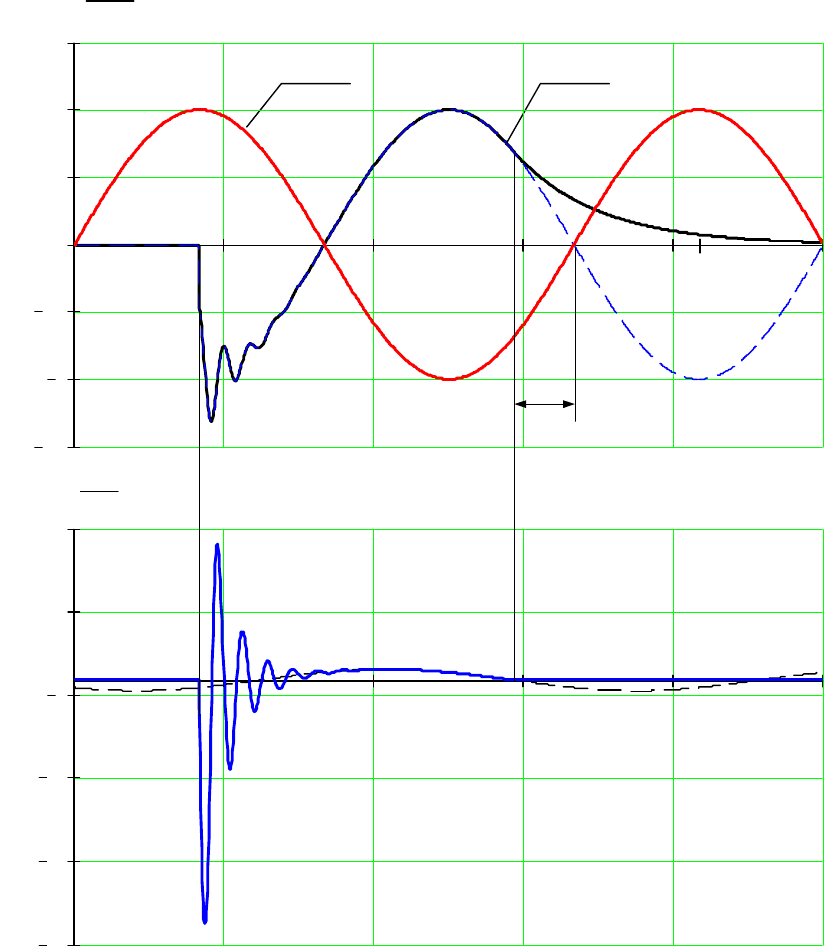
Рис. 5.9. Влияние заземления через резистор на перенапряжения
по теории Петерса и Слепяна
(показан процесс при
N
G1
∗
=
)
N Фm3Фm
uEsin(2 )Esin(=− π−β = β
3
)
. (5.21)
Угол определяется соотношением между емкостной и активной со-
ставляющими тока замыкания, то есть
3
β
100
ЭЛТИ ТПУ
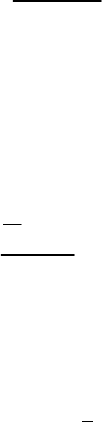
3
N
1
arctg
dG
∗
β=
+
. (5.22)
Отрезок времени от момента погасания дуги (момент ) до момента
достижения максимума напряжения на поврежденной фазе (момент )
равен
2
t
3
t
3
32
2
tt
π
+
β
−=
ω
. (5.23)
Напряжение на поврежденной фазе в момент повторного зажигания ду-
ги (момент )
3
t
()
3N
dG
2
A3 Фm Фm3
u (t ) E E sin( )e
∗
π
⎛⎞
−+β +
⎜⎟
⎝⎠
=+ β . (5.24)
В момент принужденное напряжение на неповрежденных фазах
равно . Пренебрегая, как и ранее, его изменением за половину
периода переходного емкостного тока получим
3
t
Фm
1, 5E
BM CM ФmA3 C 1
uu1,5Eu(t)(1k)(1k)
δ
== + − −
. (5.25)
Для определения влияния резистивного заземления нейтрали на
формирование перенапряжений по теории Белякова в формуле (3.50)
также учтем затухание напряжения на нейтрали за половину периода
промышленной частоты, что дает
N
(d G )
BM Фm Фm ФmC
u 1,5E (1,2E e E )(1k)(1k)
∗
−π +
δ
=+ +−−
1
. (5.26)
Как следует из кривых, представленных на рис. 5.8, эффект сниже-
ния перенапряжений существенно проявляется и при значении
N
G1
∗
<
,
начиная примерно со значения
N
G0,
∗
5
=
. Это обстоятельство является
очень важным, так как позволяет получить существенный эффект при
меньшей мощности и, следовательно, при меньшей стоимости зазем-
ляющего резистора.
6. СЕТИ С КОМБИНИРОВАННЫМ ЗАЗЕМЛЕНИЕМ НЕЙТРАЛИ
В последние годы в ряде работ [16, 19] предложено использовать
заземление нейтрали через параллельно соединенные дугогасящий ре-
актор и резистор, сопротивление которого подбирается определенным
101
ЭЛТИ ТПУ
