Васильев В.Г. Применение интеграла свертки в анализе систем автоматического управления
Подождите немного. Документ загружается.


Государственный комитет Российской Федерации
по высшему образованию
Тверской государственный технический университет
Кафедра автоматизации технологических процессов
В. Г. Васильев
Применение интеграла свертки в анализе
систем автоматического управления
Методическое пособие для студентов 3 курса спец. 5515
"Биотехнические машины, аппараты и системы"
по курсу “Управление в медико-биологических системах ”
для студентов 4 курса спец. 072000
«Стандартизация и сертификация продуктов питания»
по курсу “Основы автоматического управления”
Tверь 2002
Методические пособие предназначено для студентов,
для студентов 4 курса спец. 072000 «Стандартизация и сертификация
продуктов питания» по курсу “Основы автоматического управления” и для
студентов 3 курса спец. 5515 "Биотехнические машины, аппараты и системы"
по курсу “Управление в медико-биологических системах ”. В пособие
рассматривается применение операции свертки для решения задач анализа
систем автоматического управления.
Методическое пособие обсуждено на заседании кафедры и реко-
мендовано к печати (протокол N 2 от октября 2002 г.).
Составитель: доцент кафедры Автоматизации технологических
процессов В.Г.Васильев
(С) Тверской государственный
технический универcитет,2002
Содержание
Введение
1. Линейные инвариантные во времени системы.
2. Применение интеграла свертки для анализа реакции ЛИВ-систем на
входной сигнал.
3. Определение переходной характеристики объекта управления с
применением преобразования Лапласа и интеграла свертки.
Заключение
Использованная литература
Введение
Основные понятия связанные с интегралом свертки изложены в
методическом пособии «Интеграл свертки». Данное пособие преследует
цель показать применение этой операции для анализа систем
автоматического управления. С помощью интеграла свертки приведен вывод
некоторых основных соотношений, используемых для анализа систем
частотными методами.
1. Линейные инвариантные во времени системы
Системы, которые могут быть описаны линейными дифференциальными
уравнениями с постоянными коэффициентами, носят название линейных
инвариантных во времени систем ( ЛИВ–систем). Для таких систем сигнал
на выходе g(t), соответствующий импульсу бесконечно малой
продолжительности на входе, называется импульсной характеристикой
системы. Используются также следующие названия: весовая функция,
импульсная переходная характеристика, функция импульcной реакции и
др. Весовая функция g(t) полностью характеризует поведение ЛИВ-
системы. В одномерных физических системах, в которых независимой
переменной является время, весовая функция g(t) должна быть равна нулю
для отрицательных значений t. Такие системы называют физически
реализуемыми (или удовлетворяющие принципу причинности). В таких
системах реакцию на входное воздействие можно наблюдать только после
подачи на ее вход какого–либо воздействия. В этой связи системы,
удовлетворяющие принципу причинности, называют еще казуальными.
Линейные инвариантные во времени системы характеризуются
следующими свойствами:
Свойство линейности: если x
1
(t) и x
2
(t) – два входных сигнала, а y
1
(t) и
y
2
(t) – соответствующие им выходные сигналы, то линейная комбинация

η
1
x1(t) + η
2
x
2
(t) входных сигналов дает на выходе туже самую линейную
комбинацию выходных сигналов η
1
y
1
(t) и η
2
y
2
(t).
Свойство неизменности (инвариантности) во времени: если входной
сигнал x(t) задержать на время , так что x(t)= x(t-), то выходной сигнал
y(t) задержится на тоже самое время и будет иметь туже самую форму y(t-
) и тем же самым смещением. Это свойство обеспечивается тем, что
весовая функция системы g(t) не зависит от времени ( система не стареет
во времени).
2.Применение интеграла свертки для анализа реакции
ЛИВ-систем на входной сисгнал
2.1 Вывод основного соотношения
Для физически реализуемых ЛИВ- систем, для которых весовая функция
g(t) = 0 при t < 0, реакцию y(t) на произвольный входной сигнал x(t) можно
найти, воспользовавшись интегралом свертки
dtxgty )()()(
0
или же
dtgxty
t
)()()(
Обычно доказательство данного положения выглядит так. Пусть на вход
динамической системы подается произвольное входное воздействие x(t)
(рис 1).
Будем рассматривать значение выходной величины рассматриваемой
системы в некоторый произвольный момент времени t. С этой целью
разобъем ось времени на достаточно малые отрезки длительности Δ
каждый и построим график новой функции x’(t) , совпадающей с x(t) в
точках разбиения и остающейся постоянной в промежутках между ними (
на рис.1 этот график показан пунктиром). Выбор такой
аппроксимирующей функции объясняется двумя причинами:
1. Замена действительной функции x(t) приближенной x’(t) может быть
осуществлена со сколько угодной высокой точностью, так как при Δ → 0
функция x’(t) стремится x(t)
0
)()('lim
txtx
2. Полагая, что система линейна, можно использовать свойство линейности
(теорему сложения), согласно которому сигнал на выходе равен сумме
реакций на отдельные импульсы.
Приближенная функция x’(t) может рассматриваться как
последовательность прямоугольных импульсов длительности Δ каждый,
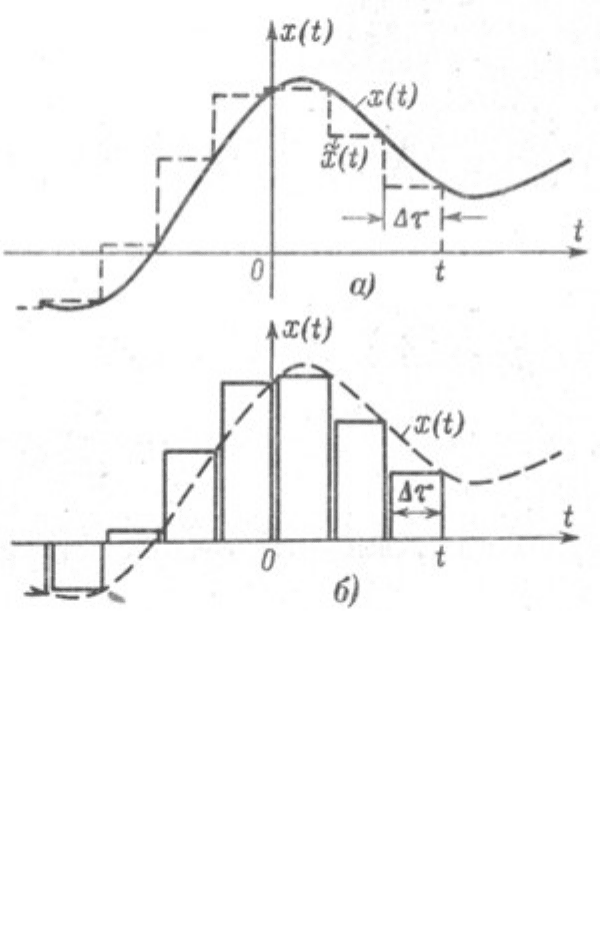
что позволяет вычислить реакцию системы на воздействие x’(t) по
известной реации на прямоугольный импульс. Обозначим: ğ(t) – реакция
системы на прямоугольный импульс, имеющий длительность Δ и
единичную площадь. Тогда сигнал на выходе системы в момент
времени t можно представить как
)()('...
...)()(')()0(')(
0
txig
txgtxgty
i
Рис. 1 Входной сигнал и его аппроксимация ступенчатой функцией
Точное решение задачи можно получить, устремив длительность
импульсов к нулю. При таком предельном переходе последовательность
прямоугольных импульсов превращается в последовательность дельта-
функций площадью x(t-)d каждая, реакция на прямоугольный импульс с
единичной площадью ğ(t) – в реакцию на дельта-функцию g(t), а
интегральная сумма при этом переходит в интеграл
dtxgty )()()(
0
Отсюда становится ясным происхождение термина «весовая» функция – ее
значения определяют «веса», с которыми берутся слагаемые в
интегральной сумме. Для физически осуществимых систем g(t) =0, t <
0.Поэтому значение интеграла не изменится, если перенести нижний
предел в -∞, что часто бывает удобным при математических выкладках.

Таким образом, интеграл свертки является наиболее общим
представлением ЛИВ-системи непрерывного времени. Применение
интеграла свертки для расчета реакции системы, посуществу, является
методом ее анализа во временной области, в то время как применение
пребразования Лапласа – методом анализа в частотной области. Выбор
метода для анализа зависит от ряда причин. К примеру, если известна
весовая функция системы, то проще сразу же воспользоваться интегралом
свертки. Если же известна передаточная функция – то проще применить
обратное преобразование Лапласа.
Чтобы проиллюстрировать применение интеграла свертки для
исследования реакции системы на входной сигнал , рассмотрим вначале
реакцию линейной системы на синусоидальный входной сигнал.
2.2 Реакция ЛИВ- системы на синусоидальный входной сигнал
Метод состоит в следующем. Аналитически удобно рассмотреть более
общий случай и считать, что входной сигнал x(t) = sinωt является
комплексной функцией. Фактически входной сигнал, воздействующий на
систему, всегда действительная функция времени. Однако, если считать
сигнал комплексным, то и выходной сигнал тоже будет комплексным, но
выходной сигнал, соответствующий Re[x(t)], равен просто Re[y(t)] (в
предположении что g(t) –действительная функция), а выходной
сигнал ,соответствующий Im[x(t)], равен Im[y(t)], где Re[] и Im[] –
действительная мнимая части комплексной функции.
Если воспользоваться формулой Эйлера, то входной синусоидальный
сигнал может быть записан в виде
tjte
tj
sincos
где j =
1
Подстановка этого сигнала в интеграл свертки дает
)()()()()(
)(
jWedegedeegdegty
tjjtjjtjtj
где
degjW
j
)()(
Функция W(jω) имеет название амлитудно-фазовой частотной
характеристикой системы. Другое ее название - комплексная передаточная
функция системы (комплексный коэффициент передачи системы ).
Учитывая что W(jω) функция комплексная ее можно представить в
виде
)()(
)(|)(|)(
jj
eAejWjW

где
)(|)(|
AjW
- амплитудно-частотная, а φ(ω) - фазо-частотная
характеристика системы. Таким образом функция W(jω) определяет и
амплитуду и фазу входного синусоидального сигнала на выходе системы.
Окончательно с учетом принятых обозначений сигнал на выходе
системы можно представить в виде
))((
)()(
j
eAty
Таким образом, при подаче на вход системы сигнала
tj
e
на ее выходе
также будут наблюдаться синосуидальной сигнал частотой ω, но с
амлитудой A(ω) и фазой φ(ω) зависящих от частоты. Форма сигнала при
этом сохраняется. Отметим также, что амлитудно-фазовая частотная
характеристика системы является прямым преобразованием Фурье весовой
функции системы.
2.3 Реакция ЛИВ- системы на произвольный входной сигнал
Пусть на вход линeйной системы подается произвольный сигнал x(t) и
требуется определить сигнал на выходе этой системы y(t) при условии, что
известна весовая функция системы g(t). Непериодической функции x(t)
будет соответствовать комплексная спектральная характеристика X(jω),
которая является прямым преобразованием Фурье входного сигнала
x(t)
dtetxjX
tj
)()(
С учетом интеграла свертки преобразование Фурье от выходного
сигнала y(t) может быть записано в следующем виде
dtdtxgedtetyjY
tjtj
])()([)()(
degdex
jtj
)()(
где υ = t - . Отсюда следует, что
Y( jω ) = W( jω ) X( jω )
(2.3.1)
Таким образом, комплексная спектральная функция выходного сигнала
системы Y(jω) равна комплексной спектральной функции входного
сигнала X(jw), умноженного на комплекcный коэффициент передачи
системы W( jω ).
Выражение (2.3.1) во французcкой технической литературе оно носит
название теоремы Планшереля, а у англичан – теоремой Бореля.
Соотношение (2.3.1) показывает, что преобразование Фурье свертки двух
функций равно произведению преобразований Фурье функций,
составляющих свертку.
Из ( 2.3.1 )находим
W( jω ) = Y( jω ) / X( jω )
Из данного соотношения следует, что при X(jω) = 1 имеет место
равенство
Y( jω ) = W( jω )
Таким образом, если на вход системы подать единичный импульс,
частотный спектр которого равен единице, то частотный спектр
выходного сигнала ( весовой функции системы) совпадает с зависимостью
комплексного коэффициента усиления системы от частоты.
Для того чтобы восстановить сигнал на выходе системы как функцию
времени, необходимо воспользоваться обратным преобразованием
Фурье
dejWjXdejYty
tjtj
)()(
2
1
)(
2
1
)(
2.4 Пример анализа реакции систем
Пусть некоторая динамическая система описывается
дифференциальным уравнением
)()(
)(
tkxty
dt
tdy
T
где T – постоянная времени , а К – коэффициент усиления системы.
Для рассматриваемой системы передаточная функция
1)(
)(
)(
Tp
K
pX
pY
pW
(2.4.2)
По таблицам преобразования Лапласа находим весовую функцию (оригинал
выражения (2.4.2) )
Tt
e
T
k
tg
/
)(
Затем используя интеграл свертки, найдем реакцию этой системы на
воздействие вида x(t) = t.
Подставив в интеграл свертки g(t) , x(t-) = t- и учитывая, кроме того, что
x(t-) = 0 при t- < 0, что позволяет положить верхний предел равным t,
получим

)]1([)()(
/
0
/
0
/
0
/ Tt
t
T
t
T
t
T
eTtkde
T
k
de
T
kt
dTe
T
k
ty
При t →
будем иметь
)()( Ttkty
Откуда следует, что сигнал на выходе будет отставать от сигнала на входе
системы на время T .
Решим эту же задачу, воспользовавшись соотношением
Y( p ) = W( p ) X(p )
Для входного сигнала x(t) = t изображение по Лапласу
2
2
1
)(
p
pX
Следовательно можно записать
pT
K
pTp
K
pY
11
1
)(
2
где α =1/T.
Далее по таблицам преобразования Лапласа находим оригинал
)(
2
1
)(
te
T
K
ty
t
После подстановки α =1/T и соответствующих упрощений получим
)]1([)(
/Tt
eTtkty
При t →
также будем иметь
)()( Ttkty
Если сравнить два рассмотренных метода, то второй метод - проще.
Однако применение интеграла свертки во многих случаях может быть
единственно возможным приемом нахождения реакции системы на
входное воздействие. Рассмотрим следующий пример.
3. Определение переходной характеристики объекта управления с
применением преобразования Лапласа и интеграла свертки
Пусть для объекта управления с передаточной функцией
,
)1)(1(
)(
21
pTpTp
K
pW

требуется найти переходную характеристику y(t), т.е реакцию системы на
единичное ступенчатое воздействие (единичный скачок).
Изображение по Лапласу единичного скачка (ступенчатой функции) есть
.
1
)(
p
pX
Учитывая, что Y(p)=W (p) X(p) можно записать
.
)1)(1(
21
2
pTpTp
K
pY
В таблицах преобразования Лапласа данное выражение отсутствует.
Поэтому, для того чтобы восстановить оригинал y(t), воспользуемся
теоремой Бореля, согласно которой, если Y(p)=X
1
(p)*X
2
(p) , то
,)()()(
0
21
dtxxty
t
Положим
,
)1)(1(
)(
21
1
pTpTp
K
pX
(3.1)
Тогда
p
pX
1
)(
2
Разделив и умножив (3.1) на 1 / (T1T3), можно записать
,
))((
1
)(
2
1
1
ppp
TT
K
pX
где α = 1/T1 и β = 1/T2.
Из таблиц преобразований Лапласа находим:
- для X1(p) оригинал есть функция
)(
11
1
)(
21
2
tt
ee
TT
K
tx
,
а для X2(p) -
)(1)(2 ttx
, т.е. единичная ступенчатая функция.
После подстановки α = 1/T1 и β = 1/T2 получим
][][
)1(
1111
1
21
)(
21
21
1
12
2
1
12
1
21
1
2
1
1
21
1
t
T
t
T
t
T
t
T
e
TT
T
e
TT
T
K
TT
eTeT
TT
TT
K
tx
Подставим полученные оригиналы в интеграл свёртки:
