Удут Л.С., Кояин Н.В., Мальцева О.П. Проектирование и исследование автоматизированных электроприводов. Часть 1. Введение в технику регулирования линейных систем Часть 2. Оптимизация контура регулирования
Подождите немного. Документ загружается.


процессов позволяют построить логарифмические частотные
характеристики: амплитудную
)(lg20)(
з.у
kL
и фазовую
( )
.
При окончательном определении качественных показателей
работы спроектированной системы автоматического регулирования для
конкретного производственного механизма или технологического
процесса кривые переходных процессов обрабатываются по
приведенным правилам. Однако, при этом должны приниматься
технологически допустимые значения погрешности
и
откладываться относительно заданного
зад
y
(а не установившегося
уст
y
) значения регулируемой координаты или относительно нулевого
0y
(а не установившегося
уст
y
) значения ошибки.
Для нахождения прямых показателей качества требуется
рассчитать или экспериментально снять переходные процессы на
выходе системы при требуемом воздействии. Расчеты могут быть
осуществлены аналитическими или численными методами. Поскольку
при аналитических методах расчета переходных процессов необходимо
определение корней характеристического уравнения замкнутой
системы, то их применение в общем плане ограничено практически 3–4-
м порядком уравнений. Прибегать к приближенным методам расчета
переходных процессов при современном уровне вычислительной
техники, по видимому, нецелесообразно.
1.4.2. Интегральные методы оценки качества регулирования
Многообразие прямых показателей качества затрудняет анализ и
сравнительную оценку кривых переходного процесса. С целью
получения общей оценки качества переходных процессов (в первую
очередь быстродействия и ошибки) в совокупности, без определения
отдельных показателей качества, применяются интегральные
показатели [10]:
• линейный интегральный показатель качества
00
)()()( ttxtxtxI dd
лин
, (1.104)
характеризующий площадь, охваченную кривой ошибки и осью
времени. Чем меньше эта площадь (
t
I min
лин
), тем больше кривая
переходного процесса приближается к кривой изменения входного
воздействия. Показатель пригоден для оценки апериодических
процессов;
• квадратичный интегральный показатель качества
0 0
22
кв
d)(d)()( ttytytyI
, (1.105)
пригоден для любой формы кривой переходного процесса.
51

Чтобы получить быстрозатухающий, но достаточно плавный
процесс, применяют улучшенную квадратичную интегральную оценку
качества
0
222
кв
d)()( ttyTtyI
, (1.106)
где T – некоторая постоянная времени.
В этом случае ограничение накладывается не только на величину
отклонения x(t), но и на скорость изменения отклонения
)(tx
.
Применяются и более сложные выражения, в которых кроме первой
ограничиваются и вторая, третья и т. д. производные от отклонения,
например вида
ttyTtyTtyI d)()()(
0
24
2
22
1
2
кв
. (1.107)
Эта оценка характеризует приближение переходного процесса к
экстремали, определяемой решением дифференциального уравнения
0)()()(
1
2
2
tytyTtyT
, (1.108)
которая соответствует более сложной кривой, чем экспонента, что
позволяет точнее задать желаемый вид переходного процесса.
Привлекательность интегральных показателей определятся
возможностью их вычисления без расчета переходных процессов, они
также хорошо подходят для оценки результатов, полученных на
вычислительных машинах.
1.4.3. Корневые методы оценки качества регулирования
Характер переходного процесса в системе определяется полным
решением дифференциального уравнения (1.1) (общим и частным) и,
следовательно, зависит как от знаменателя, так и от числителя
передаточной функции системы. Корневыми оценками качества
называют такие, которые основываются на анализе распределения
полюсов передаточной функции (1.5) (корней знаменателя) и ее нулей
(корней числителя) и позволяют судить о качестве переходных
процессов, не рассматривая самих переходных процессов. Наиболее
полно разработаны методы анализа качества по распределению полюсов
передаточной функции (корней характеристического уравнения). Они
применяются для систем, у которых числитель передаточной функции
не имеет нулей, т. е. является постоянной величиной
)(
)(
pA
k
pW
. (1.109)
Оценка качества в этом случае сводится к задаче отыскания
корней. Возможность получения решения в аналитическом виде при
этом ограничена системами 4–5-го порядков. Для систем более высоких
52

порядков приходится либо прибегать к понижению порядка (если это
возможно), либо пользоваться приближенными и, в частности,
численными методами определения корней.
Известно, что для обеспечения устойчивости САУ корни
характеристического уравнения должны располагаться в левой
полуплоскости (иметь отрицательные вещественные части).
Расположение корней принято характеризовать параметрами
, ,
(рис. 1.26). Параметр
( ) 0
, называемый степенью устойчивости,
есть расстояние от мнимой оси до ближайшего корня. Не следует
смешивать понятия "степень устойчивости" и "запас устойчивости", т. к.
они являются совершенно разными. Степень устойчивости оценивает
быстродействие системы. Параметр
, называемый
колебательностью, есть модуль отношения мнимой части
ближайшей к мнимой оси пары комплексно-сопряженных корней к
модулю их вещественной части
tg
. (1.110)
Параметр
( > 0)
есть расстояние от мнимой оси до наиболее
удаленного корня.
x
x
x
x
j
x
x
x
x
j
а б
j
j
Рис. 1.26
Оценка времени переходного процесса. Корни
характеристического уравнения, расположенные ближе всего к мнимой
оси, т. е. имеющие наименьшую по абсолютной величине
отрицательную вещественную часть, дают составляющую переходного
процесса, которая затухает наиболее медленно. Если ближайшим
является вещественный корень (рис. 1.26, а), то наиболее медленно
затухающей в переходном процессе является соответствующая ему
апериодическая составляющая и время переходного процесса
1
ln
1
ру2
t
, (1.111)
где
– зона допустимых отклонений, о. е.
При
%5
приближенное значение времени переходного
процесса
53

3
05.0
1
ln
1
)5(
2ру
t
. (1.112)
Если ближайшей к мнимой оси является пара комплексно-
сопряженных корней (рис. 1.26, б), то наиболее медленной в
переходном процессе является гармоническая составляющая. В этом
случае верхнюю границу длительности переходного процесса можно
оценить по выражению
.
1
ln
1
)(
2ру
t
(1.113)
При
%5
3
)5(
2ру
t
.
Некоторой обобщенной оценкой корней характеристического
уравнения (1.11) может служить параметр
n
n
n
n
a
a
0
210
, (1.114)
называемый среднегеометрическим корнем и являющийся мерой
быстроты протекания переходных процессов. Увеличение
0
в m раз
приводит к тому, что переходный процесс, оставаясь подобным самому
себе, будет протекать в m раз быстрее. Если качество переходного
процесса является приемлемым с точки зрения допустимого запаса
устойчивости, определяемого, например, перерегулированием, то
требуемая быстрота протекания переходного процесса может быть
обеспечена соответствующим выбором величины
0
. Для увеличения
величины
0
, как следует из (1.114), необходимо увеличивать
свободный член характеристического уравнения
0
a
. В статических
системах
ka 1
0
, в астатических
ka
0
, где k – коэффициент усиления
разомкнутой системы. Следовательно, повышение быстродействия
может осуществиться за счет увеличения общего коэффициента
усиления системы. Однако следует помнить, что это может привести к
потери устойчивости.
Оценка перерегулирования. Если ближайшей к мнимой оси
является пара комплексно-сопряженных корней, то величина
колебательности
позволяет определить приближенное значение
перерегулирования [2]
e
. (1.115)
Оценка запаса устойчивости. Запас устойчивости может быть
оценен по значению затухания за период
2
1 e
. (1.116)
Затуханием на период называют величину
100
1
21
m
mm
A
AA
, %,
54

где
1m
A
и
2m
A
– максимальные значения выходной величины через
период
2T
.
Обычно в САУ допускается затухание за один период не менее
%9890
. При
%90
допустимая величина колебательности
составляет
2 72.
, при
%98
соответственно
157.
.
Задание определенной колебательности
заставляет ограничивать
допустимую область расположения корней двумя лучами (рис. 1.26),
которые составляют с действительной осью угол
arctgarctg
.
При задании допустимых значений колебательности
и степени
устойчивости
область расположения корней должна также
ограничиваться вертикальной прямой, проходящей параллельно мнимой
оси на расстоянии
(рис. 1.26).
Расположение корней в указанной области обеспечивает
требуемый запас устойчивости, определяемый затуханием
, и
быстродействие, характеризуемое степенью устойчивости
.
Как указывалось выше, приведенные рассуждения и оценки
качества переходного процесса оказываются справедливыми лишь в
частном случае, а именно для передаточной функции вида (1.109), не
имеющей нулей. Для передаточной функции общего вида (1.5) удаление
нулей от области полюсов ведет к увеличению амплитуд собственных
колебаний переходного процесса. Это обстоятельство следует
учитывать при синтезе систем регулирования.
Корневые методы оценки качества практически редко
применяются для анализа САУ, т. к. при известных корнях построение
переходных процессов обычно не вызывает затруднений, что позволяет
оценить качество регулирования непосредственно с помощью прямых
показателей. Область применения корневых методов ограничена, как
правило, задачами синтеза. В этом случае проблема сводится к
определению параметров системы, при которых обеспечивается
нахождение корней характеристического уравнения в заданной области.
Для ее решения может быть применен метод корневого годографа [1].
Для системы третьего порядка характеристическое уравнение
0
01
2
2
3
3
aaaa
(1.117)
приводится к нормированному виду
01
23
BqAqq
, (1.118)
где
(1.121); = (1.120) = (1.119)
12
3
2
03
3
0
2
3
0
3
0
3
;;
aa
a
B
aa
a
A
a
a
q
55

3
3
0
0
a
a
– среднегеометрический корень.
Поставив в уравнение (1.118) общее выражение для корня
j
и отделяя вещественную и мнимые части, можно получить
систему уравнений
,
2
1
2
22
22
22
B
A
(1.122)
позволяющую построить в области параметров A и B диаграмму
Вышнеградского – многообразие кривых, характеризующих
распределение корней характеристического уравнения (рис. 1.27).
Граница области устойчивости характеризуется наличием пары
чисто мнимых корней. Полагая в (1.122)
0
, получим
2
=
BA ,
1
2
,
или AB = 1 – граница области устойчивости в параметрической форме
(кривая AB на рис. 1.27).
Граница области монотонных апериодических переходных
процессов. Переходный процесс будет монотонным апериодическим,
если все три корня вещественные. Приняв
0
, из (1.122) получим
027184
3322
BABABA
. (1.123)
Линии, ограничивающие область монотонных апериодических
переходных процессов, находятся приравниванием нулю
дискриминанта формулы Кардана для решения кубического уравнения
(1.123). Область монотонных апериодических процессов заключена
между кривыми CE и CF (область II, рис. 1.27). В точке С (3, 3) все три
корня
1 2
, и
3
вещественны и равны –1.
Кривая равных расстояний корней до мнимой оси находится из
условия, что все три корня имеют одинаковую вещественную часть
j
2,3
,
1
.
Линия равенства вещественных частей всех корней (кривая CD,
рис. 1.27) получается из (1.122) при использовании теоремы Виетта
2
32
1
1
2
1
= или
,
т. е. определяется уравнением
02792
3
BAA
. (1.124)
Выше линии DС вещественный корень по абсолютной величине
меньше модуля вещественной части комплексно-сопряженных корней
(расположен ближе к мнимой оси). Доминирующей в решении
переходного процесса будет апериодическая составляющая, на
которую накладывается колебательная. Ниже кривой DС ближайшими
к мнимой оси будут комплексные корни, и доминирующей
составляющей решения переходного процесса будет колебательная.
56
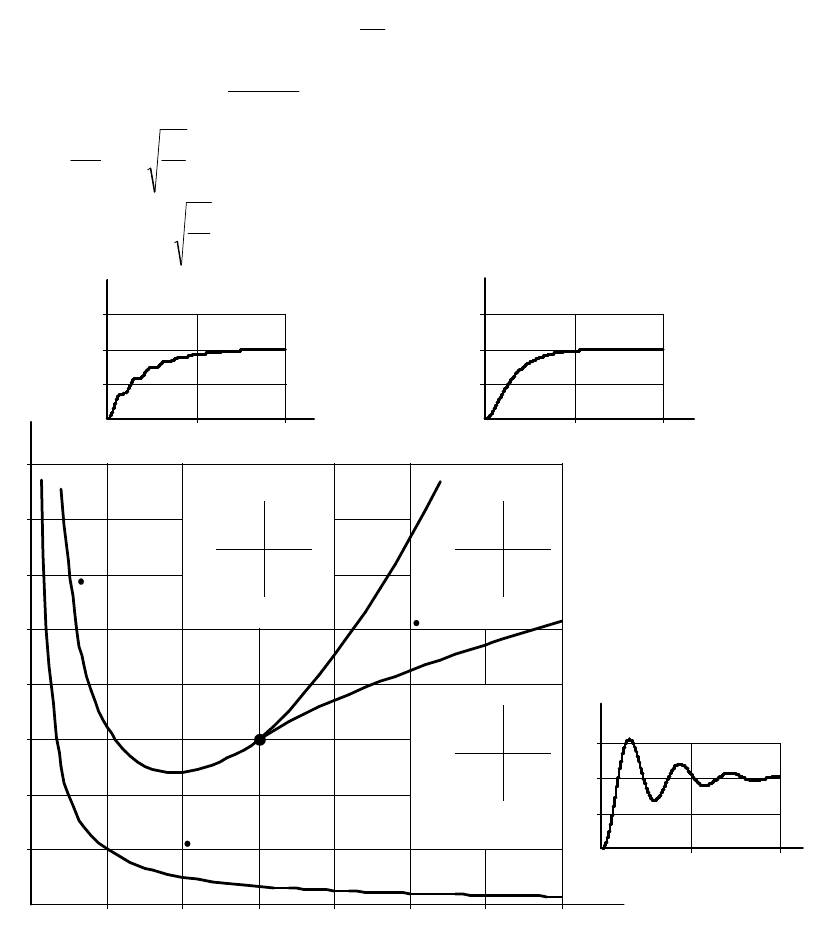
Таким образом, в области I процессы будут колебательные, в области
II – апериодические, а в области III – монотонные колебательные (без
перерегулирования).
Линии равной нормированной степени устойчивости
0
const
,
нанесенные на диаграмму Вышнеградского, характеризуют быстроту
затухания переходных процессов и могут быть построены на основании
уравнений:
0
2
00
1
AB
– в области II и III,
00
0
22
2
1
A
A
B
– в области I,
где
3
3
0
0
0
a
a
– нормированная степень устойчивости,
3
0
3
000
a
a
.
B
A
I
II
III
j j
j
x
x
x
x
x
x
xxx
1
2
3
4
5
6
7
8
1 2 3 4 5 6 7
С
Е
F
D
y
x
y
x
y
x
Рис. 1.27. Диаграмма Вышнеградского
На рис. 1.28 построены линии одинаковых значений
нормированной степени устойчивости
0
. Кривая
0
0
совпадает с
границей устойчивости. Наибольшая степень устойчивости
0
1
имеет
место в точке C с координатами A = 3, B = 3. Поэтому с точки зрения
57
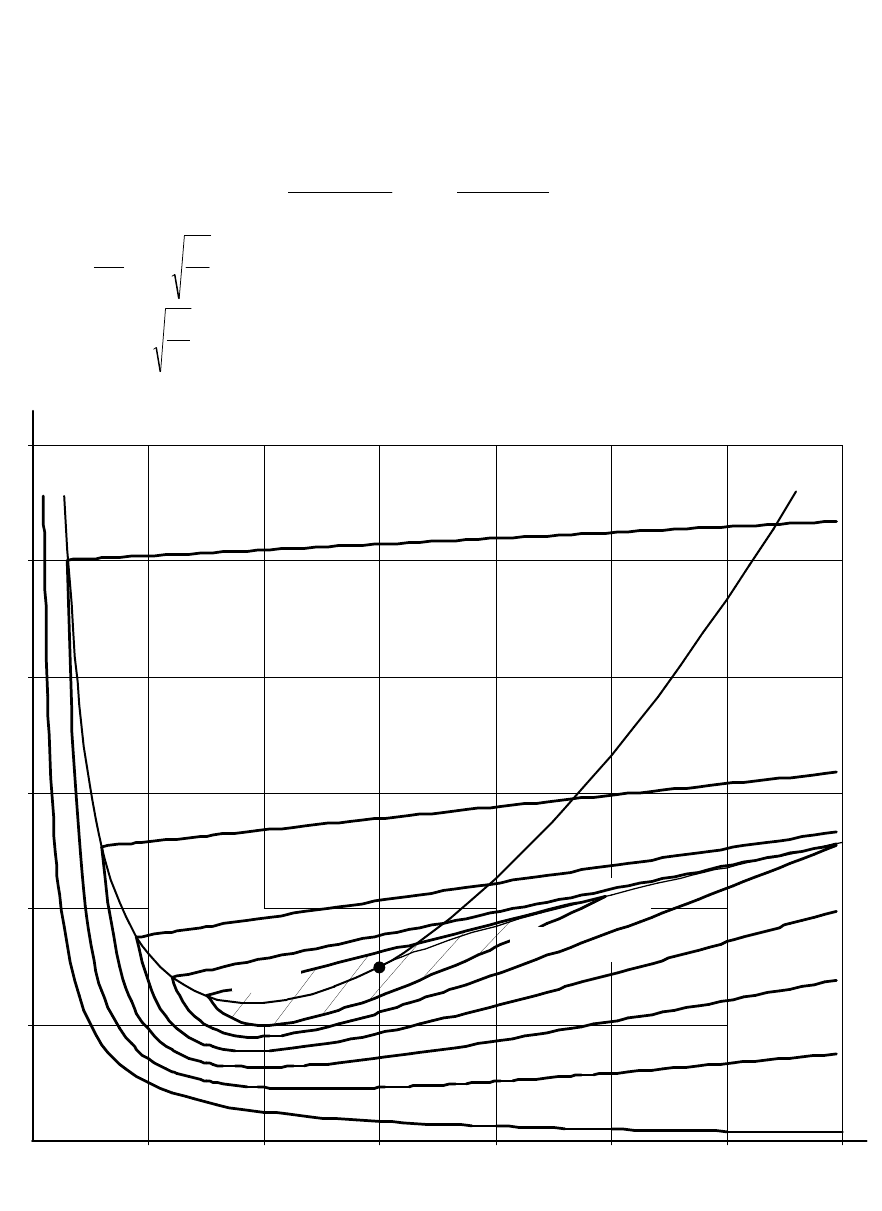
быстроты затухания переходных процессов наилучшей областью
параметров системы будет область, прилегающая к точке C, например
внутри замкнутой кривой
5,0
0
.
Линии равных значений нормированной колебательности
0
const
могут быть нанесены на диаграмму Вышнеградского в
областях I и III, где имеются комплексные корни. С учетом (1.110) из
(1.123) можно получить уравнения:
2
0
2
2
0
2
0
2
1
+1
2
= ;
1
1
2
BA
,
где
3
3
0
0
0
a
a
– нормированная колебательность;
3
0
3
000
a
a
.
2
4
6
8
10
12
1 2 3 4 5 6 7
B
A
0
01 .
0
0 2 .
0
0 3 .
0
0 4 .
0
0
0
01 .
0
0 2 .
0
0 3 .
0
0 4 .
0
0 5 .
0
0 5 .
С
II
I
III
D
E
F
Рис. 1.28. Линии равной степени устойчивости
const
0
58
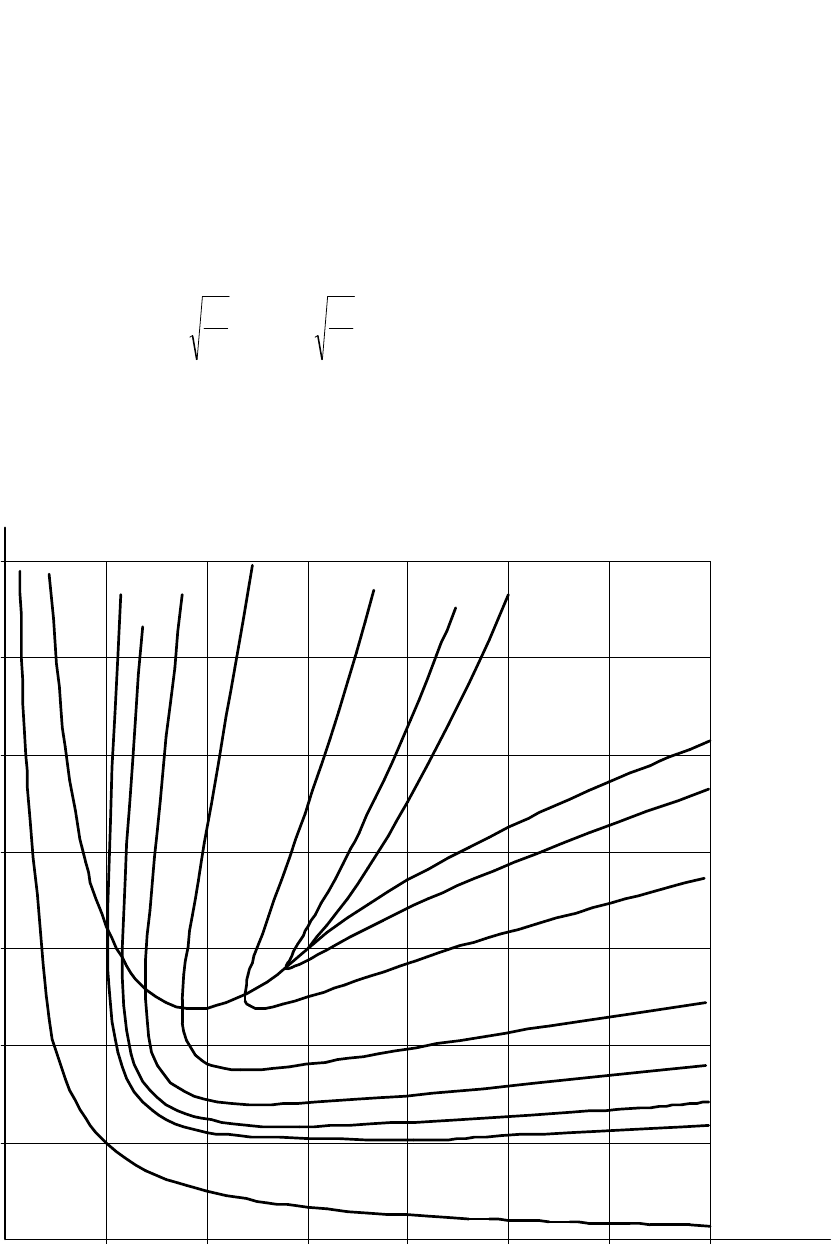
Задаваясь различными значениями
0
const
и рассматривая
как параметр, изменяя его от 0 до
, можно построить кривые равной
колебательности или равного затухания (рис. 1.29). При
0
0
получается граница апериодических переходных процессов, при
0
–
граница устойчивости.
Таким образом, если в системе третьего порядка требуется
получить заданное качество регулирования, определяемое временем
переходного процесса
)5(
2ру
t
и перерегулированием
, следует, пользуясь
выражениями (1.112, 1.113 и 1.115), задаться значениями степени
устойчивости
и колебательности
, перейти к нормированным
величинам
3
3
0
3
3
0
0
a
a
a
a
0
,
и на диаграммах рис. 1.28 и 1.29
выбрать соответствующую точку. По найденным значениям параметров
A и B с помощью формул (1.120 и 1.121) подбирают значения
коэффициентов характеристического уравнения, а затем параметры
реальной системы регулирования.
1
2
3
4
5
6
7
1 2 3 4 5 6 7
B
A
I
II
III
0
0
0
0
0
0
0
0
D
E
F
59

Рис. 1.29. Линии равных значений колебательности
const
0
Основным недостатком корневых методов, ограничивающим
область их практического применения, является то обстоятельство, что
при решении задач анализа они не дают возможности по расположению
корней точно оценить такие качественные показатели как время
переходного процесса, перерегулирование, а при синтезе САУ не
позволяют непосредственно связать прямые показатели качества с
параметрами системы.
1.4.4. Частотные методы оценки качества регулирования
При проектировании автоматизированных систем электропривода
широко используются методы частотных характеристик. Поскольку
существует связь между показателями качества по переходным
характеристикам и частотными свойствами системы, то целесообразно
сформулировать частотные показатели (критерии) качества систем
регулирования.
Показатели качества могут быть заданы по частотным
характеристикам разомкнутой системы: амплитудно-фазовой частотной
характеристике (годограф Найквиста) или логарифмическим частотным
характеристикам (ЛЧХ), или замкнутой системы: по вещественной
частотной характеристике
)(P
, амплитудной частотной
характеристике
зам
)( jW
или логарифмическим частотным
характеристикам (ЛЧХ).
Предпочтение следует отдать ЛЧХ. На рис. 1.30 приведены ЛЧХ
по управлению замкнутой системы регулирования. Они
характеризуются следующими показателями качества:
макс
з.у
)( jW
– резонансный максимум или максимальное
значение амплитудной частотной характеристики (модуль передаточной
функции);
0
)(
з.у
jW
– модуль передаточной функции при
0
или
коэффициент усиления замкнутой системы по управлению
з.у
k
;
р
– резонансная частота (частота максимума), соответствующая
макс
з.у
)( jW
. На этой частоте гармонические колебания проходят через
систему с наибольшим усилением;
сз
– частота среза замкнутой системы;
)(м
п
– граничная частота полосы пропускания замкнутой системы
(контура) по модулю, соответствующая значению модуля передаточной
функции, равному 0.707
0
)(
з.у
jW
;
60
