Удут Л.С., Кояин Н.В., Мальцева О.П. Проектирование и исследование автоматизированных электроприводов. Часть 1. Введение в технику регулирования линейных систем Часть 2. Оптимизация контура регулирования
Подождите немного. Документ загружается.

00
)()( xkxthty
. (1.31)
Амплитудно-фазовая частотная функция звена
kjW )(
, (1.32)
тогда выражения для ЛАЧХ и ЛФЧХ имеют соответственно вид
0)( ,lg20)( kL
. (1.33)
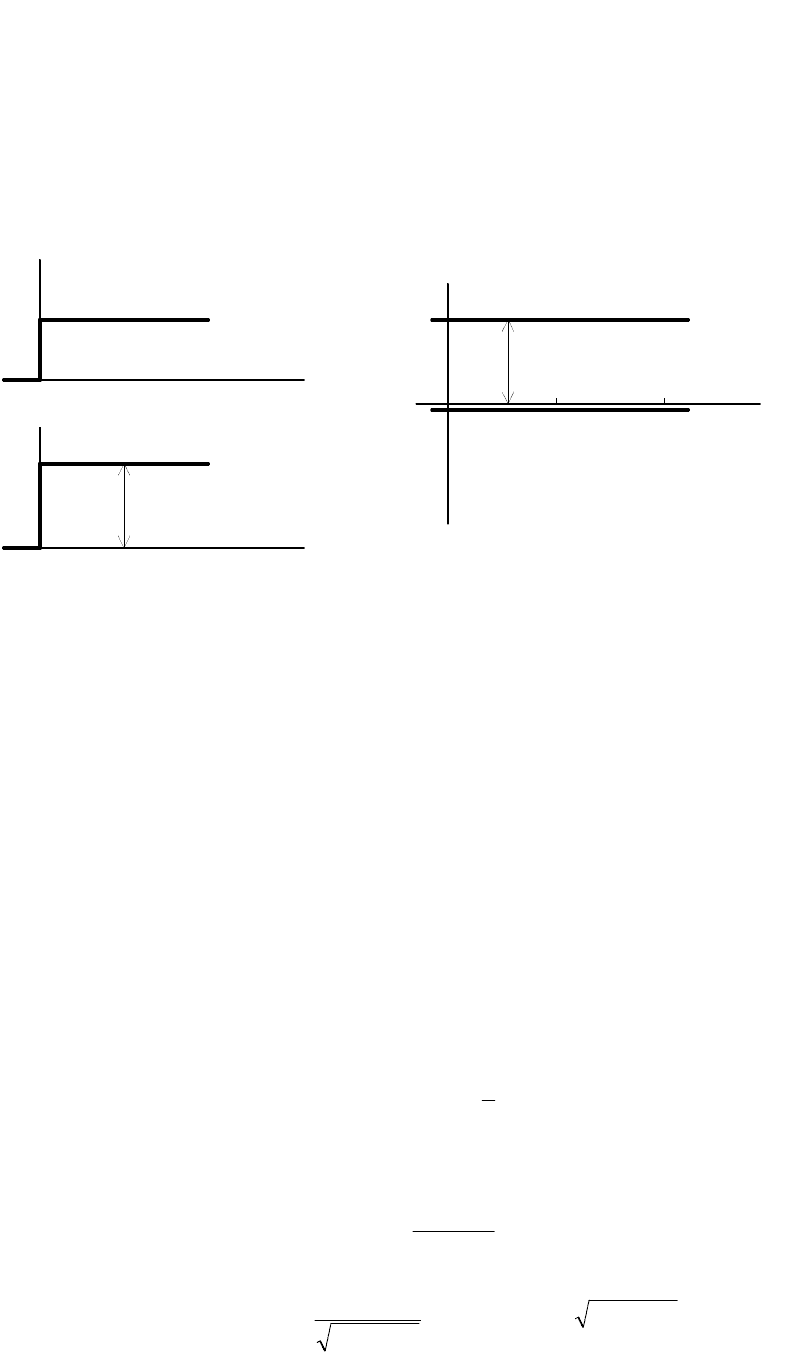
Временные и логарифмические частотные характеристики звена
приведены на рис. 1.8.
x
t
t
y
1
k
а
L
lg
L( )
( )
20lg
дБ
град
0
1
б
1 2
10 100
, с
-1
k
Рис. 1.8. Временные (а) и частотные (б) характеристики
пропорционального звена
1.2.3. Инерционные звенья
У инерционных звеньев выходная величина не следует
непосредственно за изменениями входной величины, она всегда отстает во
времени.
1. Инерционное (апериодическое) звено первого порядка
Дифференциальное уравнение и передаточная функция звена
приведены в табл. 1.1 (п. 2). Переходная функция звена при единичном
входном воздействии имеет вид
T
t
kth e1)(
, (1.34)
что соответствует апериодическому переходному процессу.
Амплитудно-фазовая частотная функция звена
Tj
k
jW
1
)(
, (1.35)
тогда
,1lg20lg20
1
lg20)(
22
22
Tk
T
k
L
(1.36)
21
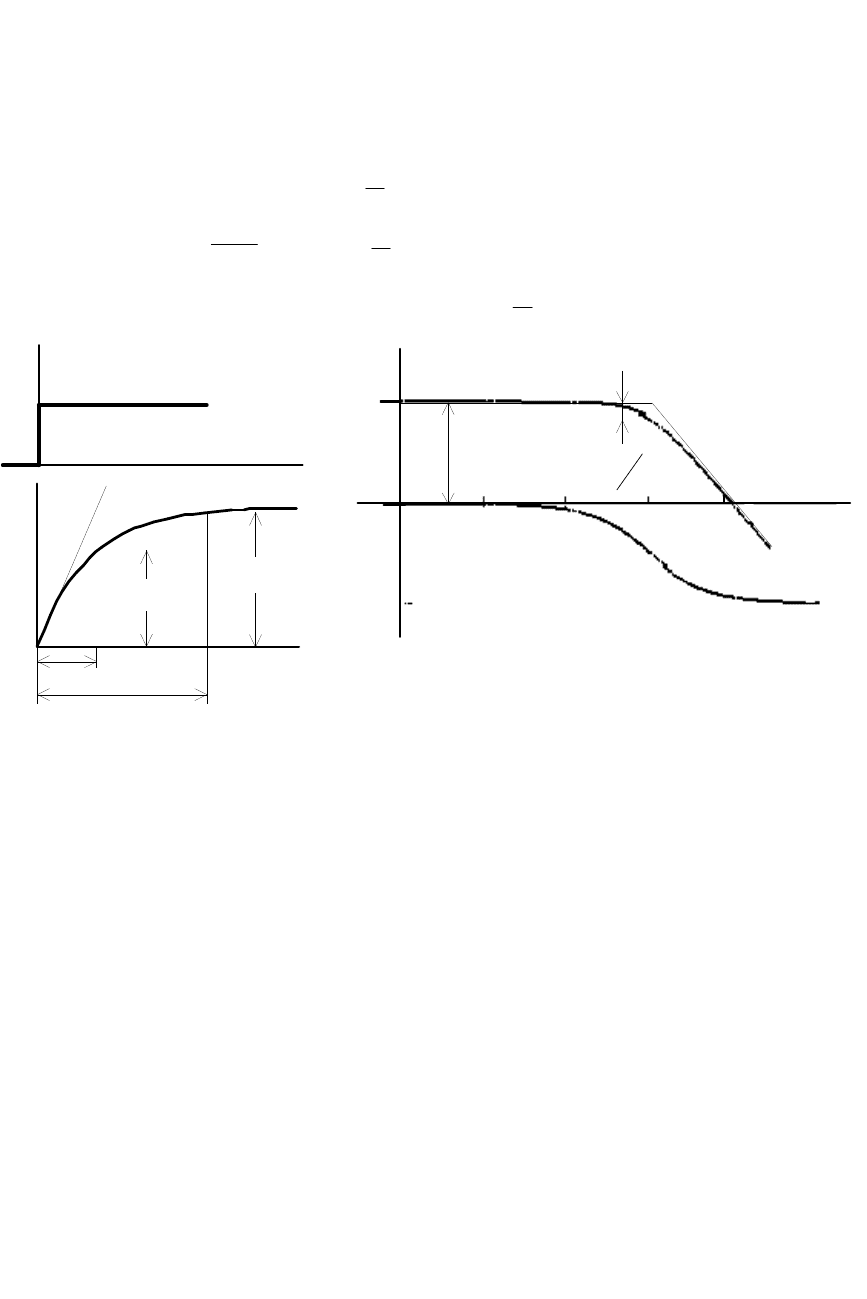
)(arctg)(arctg)( TT
. (1.37)
Временные и логарифмические частотные характеристики звена
приведены на рис. 1.9. Здесь и далее тонкими линиями показана
асимптотическая ЛАЧХ. Асимптотические прямые строятся в
соответствии с выражениями:
kL lg20)(
, при
T
1
– прямая с наклоном 0 дБ/дек;
3
lg20)(
T
k
L
, при
T
1
– прямая с наклоном -20 дБ/дек.
Ошибка в точке сопряжения при
T
1
равна 3 дБ.
град
-90
-45
дБ L
lg
-20 дБ/дек
20lg
x
t
T
t
k
1
L( )
( )
y
95%
3
63%
3 дБ
1
T
0
1
б
а
10 1000
1 2
, с
-1
T
k
Рис. 1.9. Временные (а) и частотные (б) характеристики инерционного звена
первого порядка
2. Инерционные звенья второго порядка
Дифференциальное уравнение и передаточная функция звена для
общего случая приведены в табл. 1.1 (п. 3). В зависимости от значения
коэффициента демпфирования
возможны три случая:
1.
1
– апериодическое звено второго порядка
(последовательное включение двух инерционных звеньев первого
порядка);
2.
1
– колебательное звено;
3.
0
– консервативное звено.
Апериодическое звено второго порядка
( ) 1
Передаточная функция звена приведена в табл. 1.1 (п. 3.2).
Переходная функция звена при единичном входном воздействии для
общего случая
)(
43
TT
имеет вид
22

4
3
ee
1
1)(
43
43
T
t
T
t
TT
TT
kth
, (1.38)
что соответствует монотонному процессу.
Амплитудно-фазовая частотная функция звена
43
1
2
2
2
11
1
)(
TjTj
k
TjT
k
jW
, (1.39)
тогда
,1lg201lg20lg20
21
lg20)(
2
4
22
3
2
4
2
42
2
2
1
2
TTk
TTT
k
L
(1.40)
43
2
2
2
1
arctgωarctgω
1
arctg)( TT
T
T
. (1.41)
Временные характеристики звена приведены на рис 1.10, а.
Апериодическое звено второго порядка эквивалентно двум включенным
последовательно апериодическим звеньям первого порядка и
обеспечивает монотонный апериодический переходный процесс без
перерегулирования (см. подраздел 1.4).
Переходный процесс характеризуется следующими показателями
качества:
•
4з
Tt
– время запаздывания;
•
3
4
3
43
43
н
ln T
T
T
TT
TT
t
– время нарастания;
•
(5)
ру2
)5(
ру1
tt
– время первого и окончательного вхождения в 5%-ю
зону, зависимость которого от параметров звена представлена на
рис. 1.10, в.
23

t
t
град
-180
-90
20
дБ L
L( )
( )
lg
1
4
T
1
3
T
1
3 4
T T
-20 дБ/дек
-40 дБ/дек
1
k
x
y
а
б
95%
t
з
t
ур
( )
2
5
3 дБ
3 дБ
0
1
T T
3 4
T T
T T
T
T
3 4
3 4
3
4
ln
t
н
20lg k
10 10000
4
, с
-1
Рис. 1.10. Временные (а) и
частотные (б)
характеристики и
зависимость времени
переходного процесса (в)
от отношения
постоянных времени для
апериодического звена
второго порядка
Логарифмические частотные характеристики звена приведены на
рис. 1.10, б. Асимптотическая прямая с наклоном -40 дБ/дек строится в
соответствии с выражением
43
2
43
2
lg20
1
lg20)( TT
TT
L
при
4
1
T
.
При этом ошибка в точке сопряжения при
4
1
T
равна 3 дБ.
Колебательное звено
( )0 1
Передаточная функция звена приведена в табл. 1.1 (п. 3.1).
Переходная функция звена при единичном входном воздействии имеет
вид
24
о.е. t
1
2
3
t
T
ур
( )
2
5
1
T
T
1
2
T
T
3
4
4 5 6 7 8 9 10
1 4.79 7.87
в
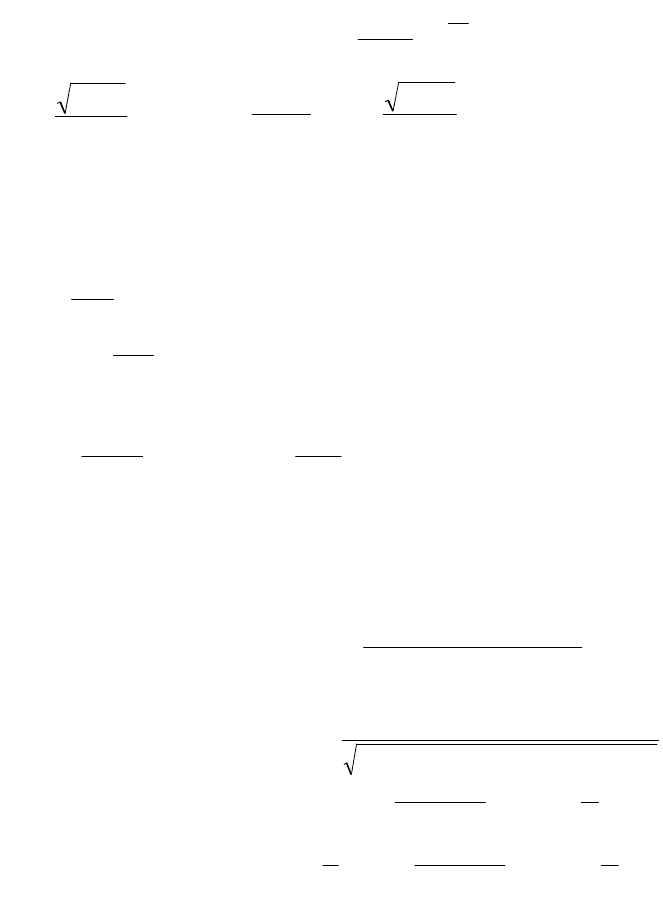
t
T
kth
k
T
t
k
sine
1
1)(
, (1.42)
где
T
k
2
1
;
2
1
arctgarctg
T
k
.
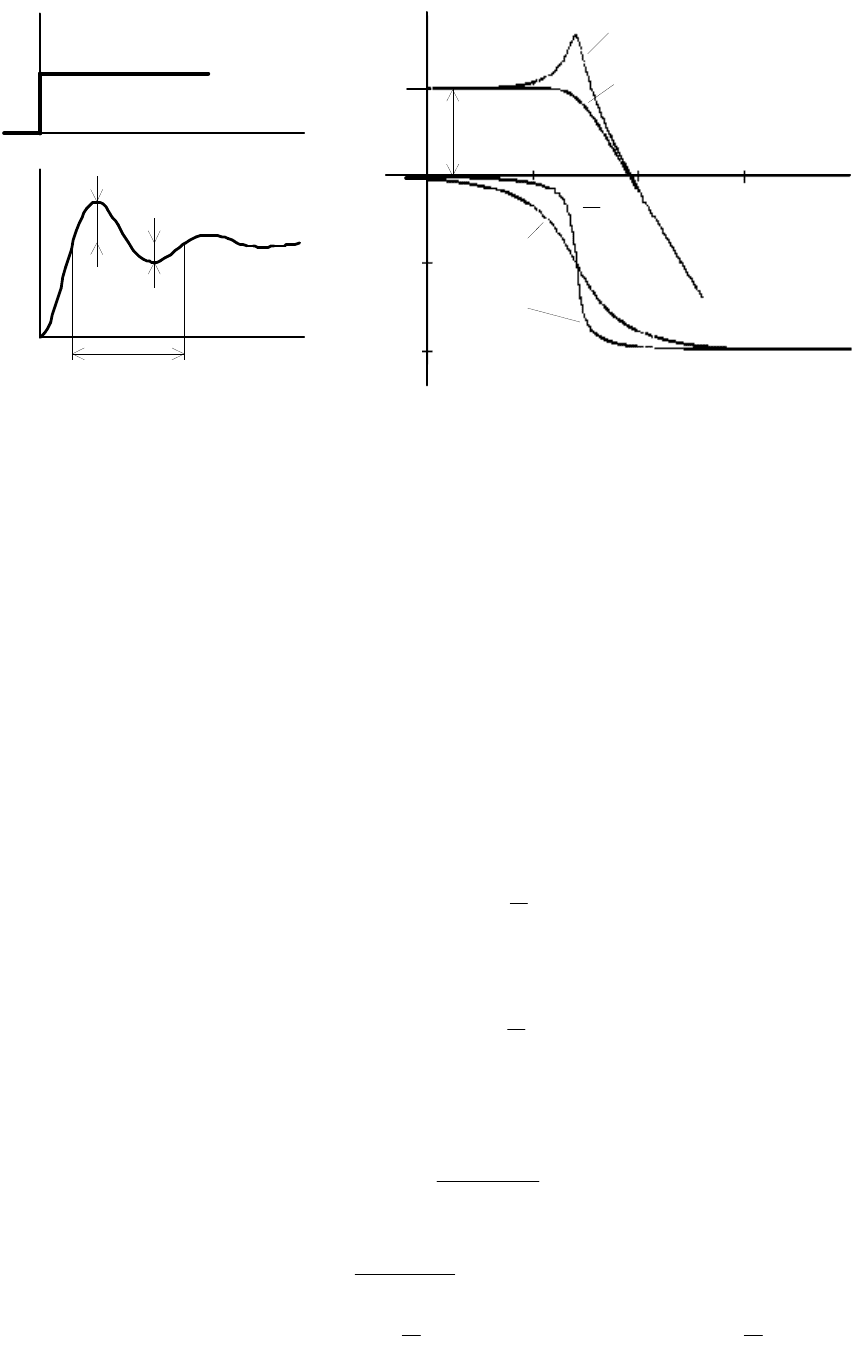
Временные характеристики звена приведены на рис. 1.11, а.
Переходный процесс имеет колебательный характер и характеризуется
следующими показателями:
k
– угловая частота свободных (собственных) колебаний, рад/с;
k
k
T
2
– период свободных колебаний, с;
T
k
k
e
1
– перерегулирование (первое) в единицах размерности
выходной координаты;
T
k
ln
, где
1
i
i
– декремент затухания, равный
отношению амплитуд соседних полуволн.
При
0
первое перерегулирование
%100
1
, а декремент
затухания
1
.
Амплитудно-фазовая частотная функция звена
TjT
k
jW
21
)(
22
, (1.43)
тогда
44222
1221
lg20)(
TT
k
L
, (1.44)
.
T
1
>при arctg
2
-=)(
T
1
<при arctg
22
22
1
2
,
1
2
)(
T
T
T
T
(1.45)
25
t
t
град
-90
-180
20
дБ
L
0,5
0,5
lg
0 5,
0 5,
-40 дБ/дек
20lg
L( )
( )
1
k
x
y
1
2
а б
T
k
0
1
1 3
1000
1
T
, с
-1
k
Рис. 1.11. Временные (а) и частотные (б) характеристики колебательного звена
Логарифмические частотные характеристики звена приведены на
рис. 1.11, б. При
0
коэффициент усиления гармонического входного
сигнала на частоте
k
стремится к бесконечно большому значению.
Полный анализ временных и частотных характеристик колебательного
звена будет произведен в подразделе 2.3. (см. п. 2.3.8).
Консервативное звено
( ) 0
Дифференциальное уравнение и передаточная функция звена
приведены в табл. 1.1 (п. 3.3). Переходная функция звена при
единичном входном сигнале имеет вид
T
t
kth cos1)(
. (1.46)
Временные характеристики звена приведены на рис. 1.12, а. При
наличии входного воздействия в звене возникают резонансные
колебания с угловой частотой
T
k
1
, периодом
TT
k
2
и
амплитудой, зависящей от величины входного сигнала,
xky
m
, где x =
const.
Амплитудно-фазовая частотная функция звена
22
1
)(
T
k
jW
, (1.47)
тогда
22
22
1lg20lg20
1
lg20)( Tk
T
k
L
, (1.48)
град0)(
при
T
1
,
град180)(
при
T
1
. (1.49)
26
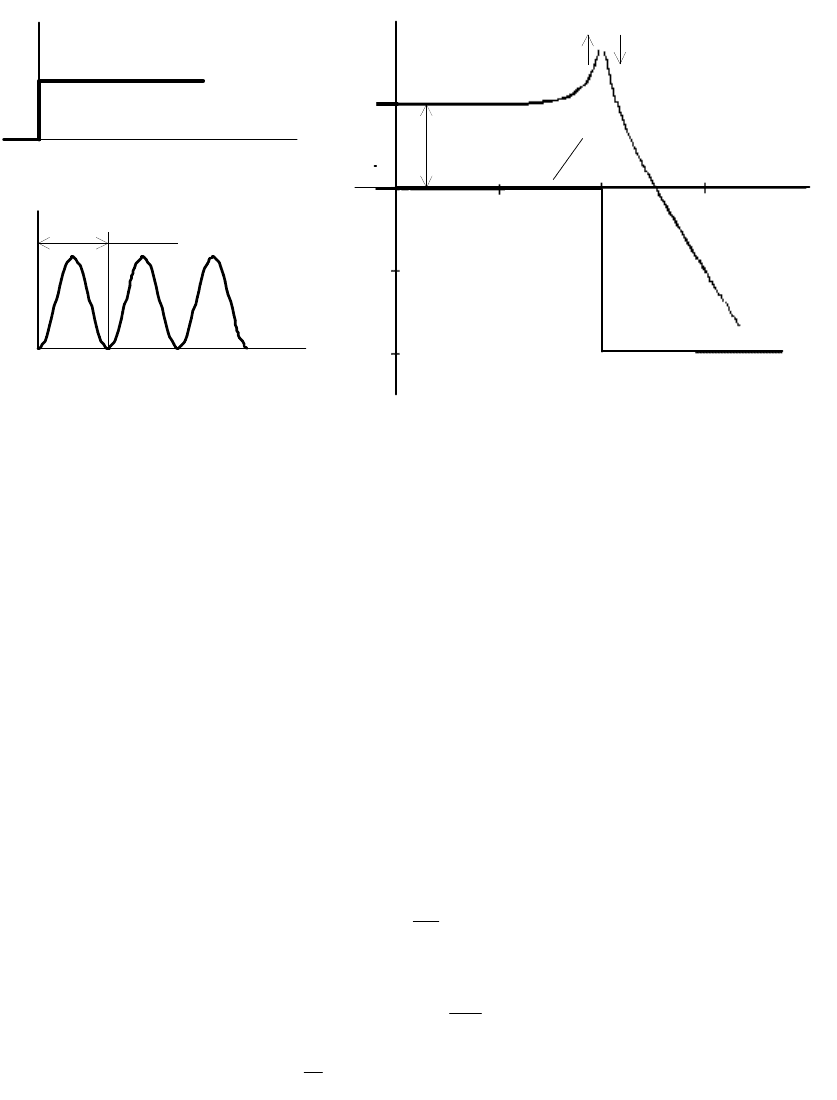
t
t
k
град
-180
-90
-40 дБ/дек
lg
дБ L
20lg
1
L( )
( )
x
y
а
б
k
1
T
T
k
0
1
1 3
10 1000
, с
-1
k
Рис. 1.12. Временные (а) и частотные (б) характеристики консервативного звена
Логарифмические частотные характеристики звена приведены на
рис. 1.12, б. Консервативное звено следует рассматривать как
идеализированное представление колебательного звена с малым
значением коэффициента демпфирования
01. .
1.2.4. Интегрирующие звенья
1. Интегрирующее идеальное звено
Дифференциальное уравнение и передаточная функция звена
приведены в табл. 1.1 (п. 4). Переходная функция звена при единичном
входном воздействии имеет вид
tkt
T
th
и
1
)(
. (1.50)
Амплитудно-фазовая частотная функция звена
j
k
jW )(
, (1.51)
тогда
lg20lg20lg20)( k
k
L
,
град 90)(
. (1.52)
Временные и логарифмические частотные характеристики звена
приведены на рис. 1.13.
27

t
t
lg
-20 дБ/дек
-90
град
LдБ
1
T
1
1
L( )
( )
x
y
k
1
T
и
20lg k
а
б
0
1
1 3
10 1000
, с
-1
и
Рис. 1.13. Временные (а и в) и
частотные (б) характеристики
интегрирующего идеального звена
При наличии входного воздействия выходная величина
интегрирующего звена изменяется непрерывно и неограниченно. Если
входную величину установить равной нулю, то выходная величина
сохраняется на достигнутом уровне сколько угодно долго. Характер
изменения выходной величины звена зависит от вида входного
воздействия (см. рис. 1.13, а и 1.13, в, а также табл. 1.2).
Таблица 1.2
Входной сигнал
(
0x
при
0t
)
Звено идеальное
интегрирующее дифференцирующее
1)( tx
tkty )(
)()( tkty
ttx 1)(
2
)(
2
t
kty
kty )(
2
1)( ttx
3
)(
3
t
kty
tkty 2)(
ttx sin1)(
t
k
ty
cos)(
tkty cos)(
28
x
t
1
2
1 2
1
2
y
t
1 2
в
k
k
2. Интегрирующее инерционное звено
Дифференциальное уравнение и передаточная функция звена
приведены в табл. 1.1 (п. 8). Переходная функция звена при единичном
входном воздействии имеет вид
T
t
T
t
TtkTt
T
ty e1e1
1
)(
и
. (1.53)
Амплитудно-фазовая частотная функция звена
jT
k
jW
2
)(
, (1.54)
тогда
22
1
lg20)(
T
k
L
.arctg
2
)( ,1lg20lg20
22
TT
k
(1.55)
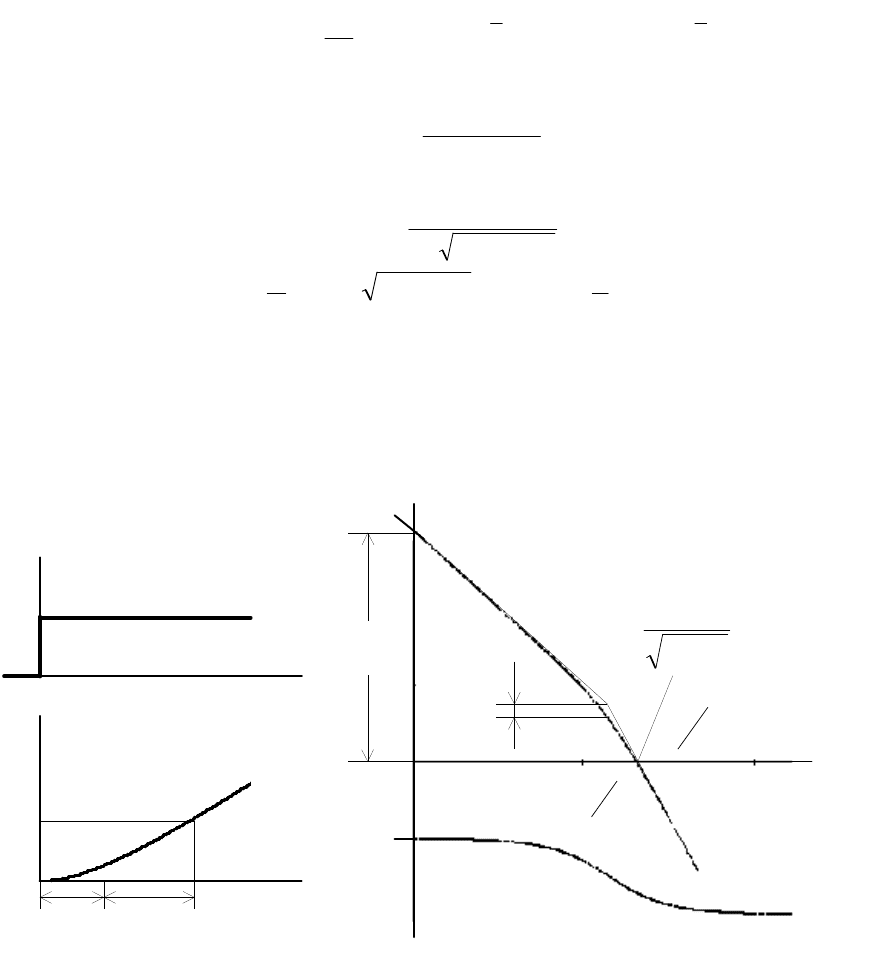
Временные и логарифмические частотные характеристики звена
приведены на рис. 1.14. Звено можно рассматривать как
последовательное включение двух звеньев: апериодического с
инерционной постоянной T и интегрирующего с постоянной
интегрирования
и
T
.
t
1
x
а
б
1
y
t
T
T
и
LдБ
град
-180
-90
-20 дБ/дек
-40 дБ/дек
L( )
( )
lg
3 дБ
1
T
и
1
T
1
T T
и
0
1
20lg k
1 2
100
, с
-1
Рис. 1.14. Временные (а) и частотные (б) характеристики инерционного
интегрирующего звена
1.2.5. Дифференцирующие звенья
1. Дифференцирующее идеальное звено
29

Дифференциальное уравнение и передаточная функция звена
приведены в табл. 1.1 (п. 5). Переходная функция звена при единичном
входном воздействии имеет вид
)()()(
д
tktTth
, (1.56)
где
( )t
– дельта-функция – предельно короткий импульсный сигнал,
площадь которого равна единице при длительности, равной нулю, и
высоте, равной бесконечности. Таким образом, переходная функция
идеального дифференцирующего звена представляет собой бесконечно
тонкий импульс с площадью k.
Амплитудно-фазовая частотная функция звена имеет вид
д
)( jTjW
, (1.57)
тогда
.град90)( ,lg20lg20lg20)(
дд
TTL
(1.58)
Временные и логарифмические частотные характеристики звена
приведены на рис. 1.15. Сигнал на выходе идеального
дифференцирующего звена появляется только при изменении входного
воздействия.
t
t
lg
+20 дБ/дек
L( )
( )
L
1
x
y
дБ
град
90
0
а б
0
1
1
T
д
100
1
1000
, с
-1
Рис. 1.15. Временные (а, в) и
частотные (б) характеристики
дифференцирующего идеального
звена
Характер изменения выходной величины звена зависит от вида
входного воздействия (см. рис. 1.15, а, в и табл. 1.2). При скачке
30
x
t
1
1
y
t
в
T
д
t
x
y
x
t
T
д
