Туркин Д.Г. Математические задачи энергетики. Методические указания
Подождите немного. Документ загружается.


Для схемы, представленной на рисунке 2.1, полная матрица соединений имеет
вид:
М
=
-1 1 0 0 0
0 -1 0 -1 -1
0 0 -1 1 0
1 0 1 0 1
а сокращенная, без строки соответствующей базисному узлу
М =
-1 1 0 0 0
0 -1 0 -1 -1
0 0 -1 1 0
Покажем возможность восстановления матрицы соединений для
балансирующего узла по сокращенной матрице соединений:
-1 1 0 0 0
MnM
tб
= -
1 1 1
0 -1 0 -1 -1 = 1 0 1 0 1
0 0 -1 1 0
Матрица соединений позволяет записать первый закон Кирхгофа (узловое
уравнение) в матричной форме:
M I = J, (2.7)
где I = (I
i
) – столбец токов в ветвях, i = 1 ,…, m;
J = (J
i
) – столбец задающих токов в узлах, i = 1 ,…, n.
Используя выражение (2.7) можно определить матрицу токов в
разомкнутой схеме:
I = M
p
-1
J = C
p
J. (2.8)
Матрица распределения токов С
р
=
1
p
M
определяет коэффициенты
распределения токов по разомкнутой схеме.
Ее строки соответствуют ветвям схемы, а столбцы – независимым, узлам.
Каждый столбец i этой матрицы определяет путь графа от узла i до узла
баланса (опорной вершины) схемы.
41
Положительная единица означает, что соответствующая ветвь входит в
состав данного пути с тем же направлением, а отрицательная – с
противоположным.
2
3
4
1
3
1 2
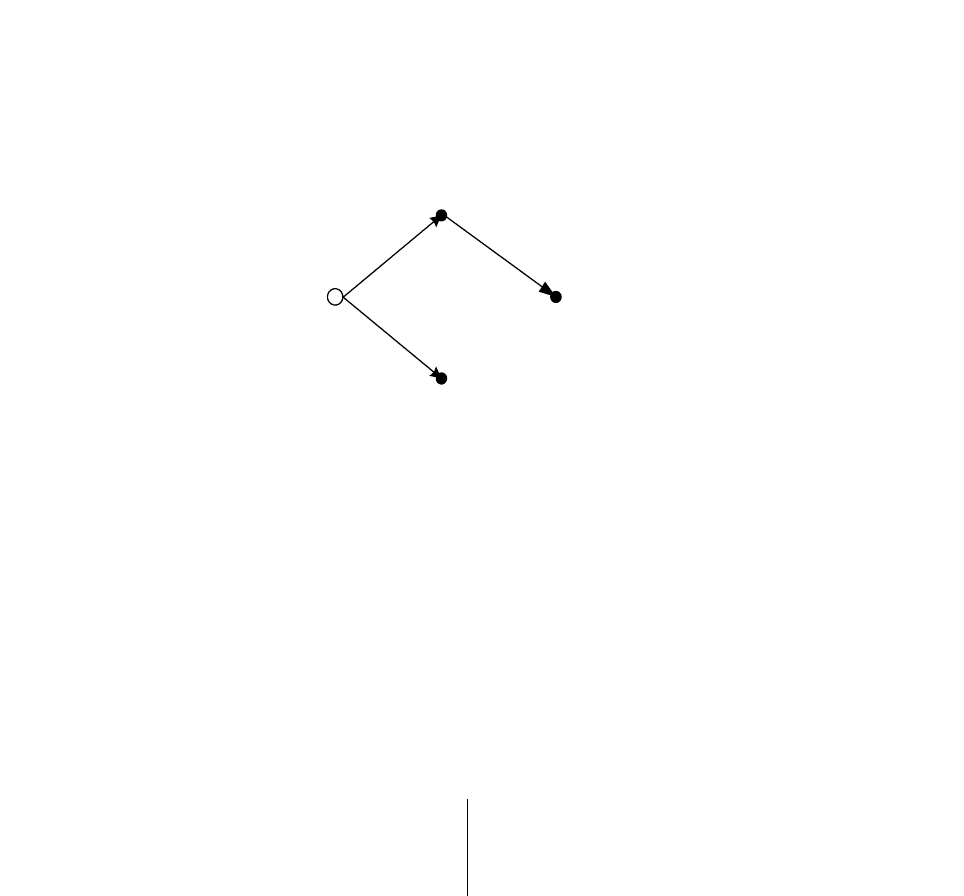
Рисунок 2.3- Пример разомкнутой схемы замещения
Нуль показывает, что данная ветвь не участвует в составе
соответствующего пути графа. Строки матрицы С
р
отражают состав путей
графа и направление каждой из ветвей. Каждый путь графа в данном случае
соответствует пути прохождения рассматриваемого задающего тока от
соответствующего узла к узлу баланса.
Для схемы, приведенной на рисунке 2.3 матрица С
р
имеет вид:
Ср =
-1 -1 0
0 -1 0
0 0 -1
Матрица соединений позволяет определить матрицу напряжений на
ветвях по матрице узловых напряжений:
U
в
= M
t
U
, (2.9)
где U
- столбец напряжений всех узлов (узловых напряжений), включая
базисный;
M
t
– транспонированная полная матрица соединений.
В практических задачах достаточно часто узловые напряжения
целесообразно определять относительно балансирующего узла, т.е. как падения
напряжения от независимых узлов до балансирующего.
Тогда выражение для падений напряжений на ветвях примет вид:
42

U
в
= M
t
U
D
, (2.10)
где U
D
= (U
i
– U
б
) – матрица узловых напряжений относительно
балансирующего узла.
2.3 Матрица контуров (вторая матрица инциденций)
Матрица контуров N служит для обобщенного аналитического
представления соединений ветвей схемы в независимые замкнутые контуры.
Строки второй матрицы инциденций N соответствуют номерам
независимых замкнутых контуров схемы, а столбцы — номерам ветвей.
Наличие соединений здесь также определяется коэффициентами
инцидентности +1, -1 и 0. При этом должно быть выбрано направление обхода
каждого контура (независимого, замкнутого).
Положительная единица показывает, что данная ветвь входит в состав
рассматриваемого контура и имеет то же направление, что и выбранное
направление контура.
Отрицательная единица показывает, что данная ветвь входит в состав
рассматриваемого контура, но имеет направление, противоположное
направлению контура.
Нуль показывает, что данная ветвь не входит в состав рассматриваемого
контура. На пересечении строки i матрицы N (соответствует контуру i схемы) и
столбца j (соответствует ветви j схемы) помещается коэффициент в
соответствии с приведенными выше показателями соединений.
Каждая строка матрицы показывает, какие ветви входят в состав
соответствующего независимого замкнутого контура и с каким направлением
относительно направления контура.
Каждый столбец той же матрицы показывает, в состав каких независимых
замкнутых контуров входит данная ветвь и совпадает ли ее направление с
направлениями этих контуров.
43

1
2
3
4
1 2
3 4
5
I
II
Рисунок 2.4- Пример схемы с выбранными направлениями обхода контуров
Для схемы, представленной на рисунке 2.4 матрица контуров имеет вид
N =
-1 -1 1 1 0
-1 -1 0 0 1
Матрица контуров позволяет получить матричное уравнение второго
закона Кирхгофа:
NZ
в
I = E
к
, (2.11)
где E
к
= NE – столбец контурных ЭДС, представляющий собой алгебраические
суммы ЭДС ветвей, входящих в каждый независимый контур.
Т.е. используя матрицы М и N можно получить уравнения состояния
электрический цепи (формулы 2.7 и 2.11) в матричном виде.
2.4 Обобщенное уравнение состояния
Если матрицы М и NZ
в
рассматривать как блоки объединенной матрицы
параметров схемы замещения:
М
А =
NZ
в
а матрицы J и E
к
рассматривать как блоки объединенной матрицы исходных параметров
режима:
J
F =
E
к
можно получить обобщенное уравнение состояния электрической цепи:
44

АI = F. (2.12)
Здесь матрица А является квадратной и полученное уравнение состояния
можно решить относительно матрицы токов ветвей:
I = А
-1
F = ВF. (2.13)
зная которые, можно определить все остальные параметры рабочего режима
непосредственно (без решения какой-либо системы уравнений).
2.5 Разделение схемы на дерево и хорды
Разделение схемы на дерево и хорды позволяет упростить решение ряда
практических задач.
Дерево — это наименьший связанный подграф, содержащий все узлы
замкнутой схемы. Число ветвей, входящих в состав дерева схемы, на единицу
меньше числа узлов всей схемы, или равно числу независимых узлов схемы.
Такая разомкнутая схема получается путем исключения ветвей,
входящих в независимые замкнутые контуры схемы.
Каждый замкнутый контур схемы размыкается, если исключается одна из
входящих в него ветвей. Если поочередно разомкнуть все независимые
замкнутые контуры, то одновременно разомкнутся и все прочие замкнутые
контуры; останется разомкнутая часть схемы — дерево.
Остальная часть схемы, состоящая из исключенных ветвей, не вошедших
в дерево схемы, называется хордами, или соединениями графа.
Число ветвей хорд равно числу независимых контуров схемы. Подграф в
виде хорд может содержать замкнутые контуры, он может получиться и
несвязанным.
Замкнутая схема, изображенная на рисунке 2.4, содержит два
независимых замкнутых контура. Поэтому достаточно исключить две ветви,
чтобы оставшиеся соединяли все узлы, т. е. составляли дерево схемы.
Одна и та же схема может быть разделена на дерево и хорды по-разному.
Обычно число вариантов такого разделения получается достаточно большим.
45
Для упрощения решения должны быть наложены некоторые дополнительные
условия.
1) Вначале нумеруются ветви, входящие в дерево схемы, а затем хорды.
2) При нумерации ветвей дерева схемы стремятся обеспечить совпадение
номеров ветвей и относящихся к ним узлов, так как число ветвей
дерева равно числу независимых узлов.
При этом на главной диагонали первой матрицы инциденций для
дерева схемы должны располагаться единицы (положительные или
отрицательные). Можно выбрать такие направления ветвей, что эти
единицы будут иметь один и тот же знак.
В общем случае единицы будут располагаться и на других местах
матрицы.
3) Хорды нумеруются в той же последовательности, в какой
пронумерованы соответствующие независимые контуры.
4) Направления обхода независимых контуров должны совпадать с
направлениями соответствующих хорд.
Если схема разделена на дерево и хорды, матрицы инциденций состоят из
двух подматриц или блоков:
М = |M
M
|, (2.14)
N = |N
N
|, (2.15)
где M
, N
- блоки, относящиеся к дереву; M
, N
- блоки, относящиеся к хорде.
1
2
3
4
1 2
3
1
2
3
4
4
5
а) б)
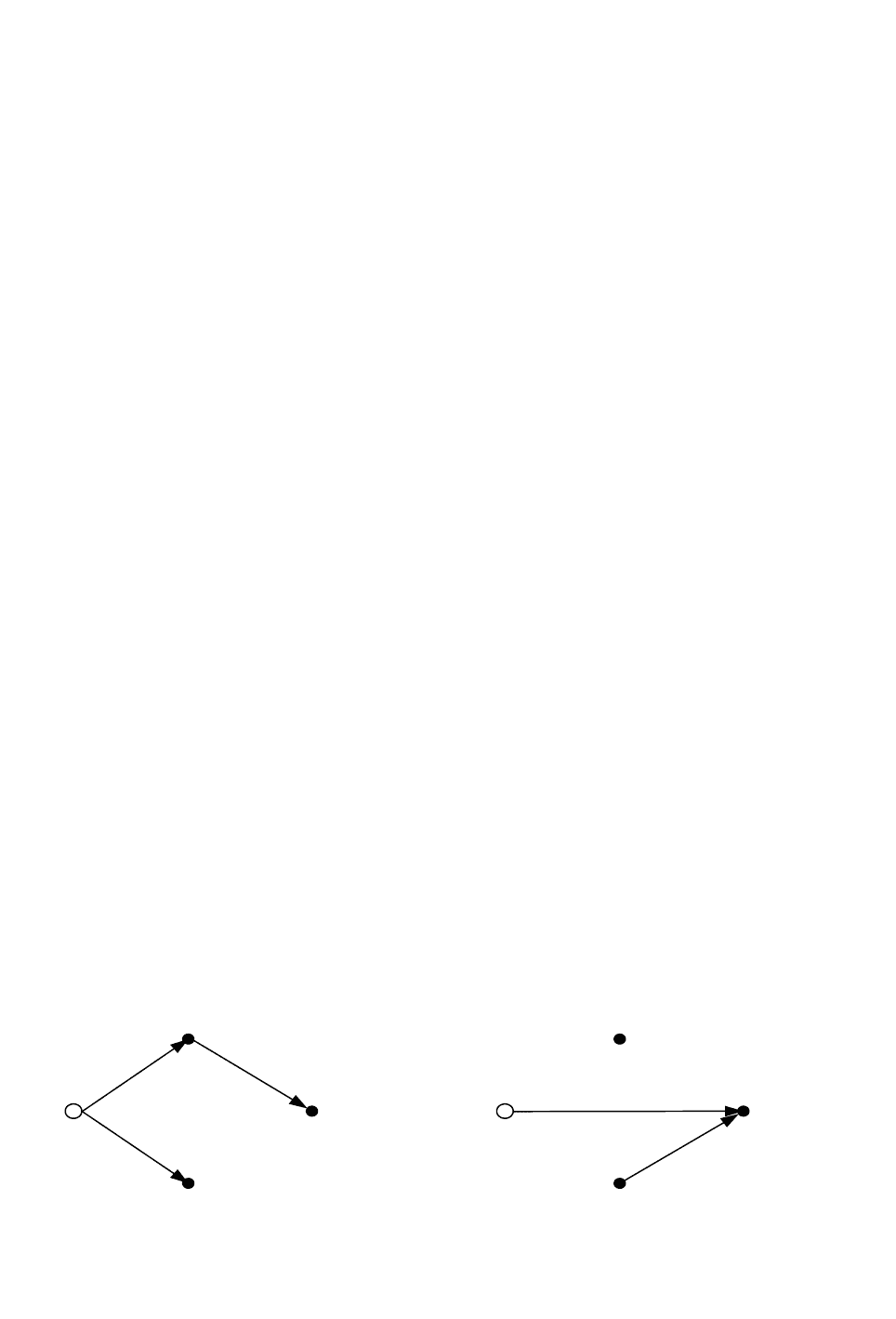
Рисунок 2.5- Разделение схемы на дерево (а) и хорду (б)
46
Составим блоки матриц для схемы, изображенной на рисунке 2.4,
разделенной на дерево и хорду как показано на рисунке 2.5.
М
=
-1 1 0
0 -1 0
0 0 -1
Т.е. выполнение первого и второго условия дает единичную диагональ
матрицы М
.
М
=
0 0
-1 -1
1 0
N
=
-1 -1 1
-1 -1 0
N
=
1 0
=1
0 1
Т.е. выполнение третьего и четвертого условия дает квадратную
единичную матрицу N
.
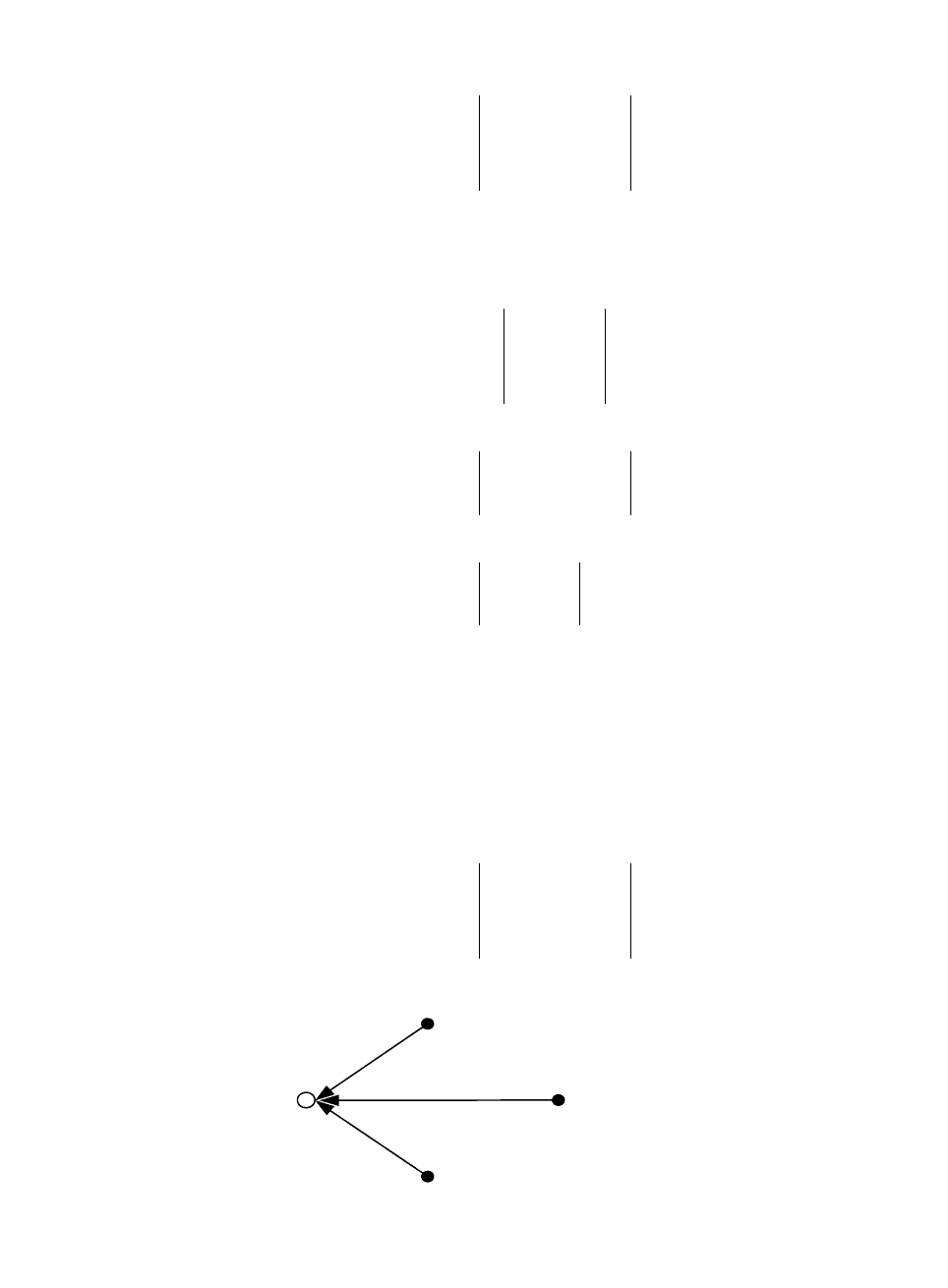
В частном случае, когда дерево схемы состоит только из ветвей,
конечной вершиной которых является базисный узел, матрица соединений для
этого дерева (рисунок 2.6) будет единичной.
М
=
1 0 0
0 1 0
0 0 1
1
2
3
4
1
3
2
Рисунок 2.6- Пример дерева схемы
47

2.6 Топологические свойства графа
Матрица М полностью определяет схему соединений, поэтому, зная ее,
можно найти и матрицу N. Для этого используется топологическое свойство
графов:
NM
t
= 0. (2.16)
Выражение (2.16) можно использовать для получения соотношения
между блоками матриц М и N. Действительно, из записи этого условия при
разделении матриц М и N на блоки
N
N
M
t
=0
M
t
получаем выражение
N
M
t
+ N
M
t
= 0
или, с учетом преобразований
N
= –N
M
t
M
t
-1
= –N
M
t
С
0t
,
где С
0
= M
-1
– матрица коэффициентов распределения токов для дерева.
Если при разделении схемы на дерево и хорду выполнялись условия три
и четыре, то N
= 1 и получаем выражение:
N
= –M
t
M
t
-1
= –M
t
С
0t
. (2.17)
Пример. Определить матрицу контуров для схемы на рисунке 2.4,
которая разделена на дерево и хорду по рисунку 2.5.
С
р
= С
0
=
-1 -1 0
0 -1 0
0 0 -1
M
=
0 0
-1 -1
1 0
N
= –M
t
С
0t
=
0 -1 1
0 -1 0
1 0 0
-1 -1 1
-1 -1 0
1 1 0 =
0 0 1
48

Окончательно матрица контуров для схемы, с учетом единичной
матрицы N
:
N = |N
N
| =
-1 -1 1 1 0
-1 -1 0 0 1
В некоторых случаях для упрощения расчета может быть использовано
произведение матриц М на M
t
, приводящее к квадратной матрице порядка у. Ее
строки и столбцы соответствуют узлам схемы.
На главной диагонали получаются суммарные числа ветвей, соединенных
с каждым данным узлом. На пересечении строки i и столбца j появляется или
отрицательная единица, или нуль. Отрицательная единица показывает, что узлы
i и j связаны ветвью. Нуль показывает, что такая связь отсутствует.
Для схемы на рисунке 2.4 получаем:
ММ
t
=
-1 1 0 0 0
-1 0 0
2 -1 01 -1 0
0 -1 0 -1 -1
0 0 -1 = -1 3 -1
0 0 -1 1 0 0 -1 1 0 -1 2
0 -1 0
Произведение матриц NN
t
показывает количество ветвей, принадлежащих
независимым контурам:
NN
t
=
-1 -1
=
-1 -1 1 1 0 -1 -1 4
-1 -1 0 0 1 1 0 3
1 0
0 1
2.7 Решение уравнений состояния
Используя обобщенное уравнение состояния (2.13) определим значения
токов в ветвях сложной схемы.
Для схемы замещения, содержащей ЭДС в ветвях и отсутствии взаимных
сопротивлений между ветвями дерева и хорды, значения токов для ветвей
49

хорды, при подстановке в (2.13) значений матриц А и F с учетом разделения на
блоки, определяются по выражению:
I
= (Z
+ N
Z
N
t
)
-1
(NE – N
Z
C
0
J) , (2.18)
где Z
и Z
- диагональные матрицы сопротивлений для ветвей дерева и
хорды соответственно;
N
– матрица контуров для дерева;
N
t
– транспонированная матица контуров для дерева;
Е – вектор ЭДС ветвей;
J – вектор задающих токов узлов;
С
0
– матрица коэффициентов распределения для дерева.
Для той же схемы значения токов для ветвей дерева определяются по
выражению:
I
= C
0
(J - M
I
), (2.19)
где М
- матрицы соединений для хорды.
Контрольные вопросы
1. Схема замещения как связанный граф – общие определения.
2. Составление первой матрицы инциденций.
3. Узловое уравнение для схемы замещения.
4. Разделение схемы замещения на дерево и хорды.
5. Составление второй матрицы инциденций.
6. Разделение матриц инциденций на блоки в соответствии с разделением
схемы замещения на дерево и хорды.
7. Топологические свойства графа – получение матрицы контуров по
матрице соединений.
8. Свойства матрицы произведений ММ
t
и NN
t
.
9. Выражение напряжений на ветвях схемы.
10. Составление матрицы распределения токов С
р
.
50
