Трофимова Т.И. Курс физики
Подождите немного. Документ загружается.

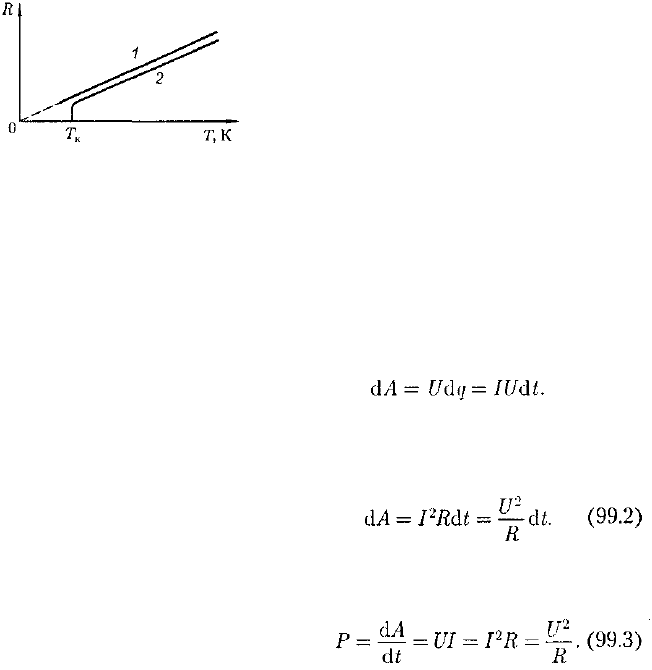
Рис. 149
Зависимость сопротивления от тем-
пературы (98.6) представлена на рис. 149
(кривая 1). При низких температурах
наблюдается отступление от этой зави-
симости.
Впоследствии было обнаружено, что
сопротивление многих металлов (на-
пример, Al, Pb, Zn и др.) и их сплавов
при очень низких температурах Т
к
(0,14 — 20 К), называемых критиче-
скими, характерных для каждого веще-
ства, скачкообразно уменьшается до
нуля (кривая 2), т.е. металл становит-
ся абсолютным проводником. Впервые
это явление, названное сверхпроводи-
мостью, обнаружено в 1911 г. Г. Камер-
линг-Оннесом для ртути.
Явление сверхпроводимости объяс-
няется на основе квантовой теории.
Практическое использование сверхпро-
водящих материалов (в обмотках сверх-
проводящих магнитов, в системах па-
мяти ЭВМ и др.) затруднено из-за их
низких критических температур. В на-
стоящее время обнаружены и активно
исследуются керамические материалы,
обладающие сверхпроводимостью при
температуре выше 140 К.
На зависимости электрического со-
противления металлов от температуры
основано действие термометров со-
противления, которые позволяют по
градуированной взаимосвязи сопро-
тивления от температуры измерять тем-
пературу с точностью до 0,001 К. Тер-
мометры сопротивления, в которых в
качестве рабочего вещества использу-
ются полупроводники, изготовленные
по специальной технологии, называют-
ся термисторами. Они позволяют из-
мерять температуру с точностью до
миллионных долей кельвин.
§ 99. Работа и мощность тока.
Закон Джоуля—Ленца
Рассмотрим однородный провод-
ник, к концам которого приложено на-
пряжение U.
За время dt через сечение проводника
переносится заряд dq — Idt. При этом
силы электростатического поля и сторон-
ние силы совершают работу [см. (84.6)]
(99.1)
Если сопротивление проводника R,
то, используя закон Ома (98.1), полу-
чим, что работа тока
Из (99.1) и (99.2) следует, что мощ-
ность тока
Если сила тока выражается в ампе-
рах, напряжение — в вольтах, сопротив-
ление — в омах, то работа тока выража-
ется в джоулях, а мощность в ваттах. На
практике применяются также внесис-
темные единицы работы тока: ватт-час
(Вт • ч), киловатт-час (кВт • ч); 1 Вт • ч —
работа тока мощностью 1 Вт в течение
1 ч; 1 Вт • ч = 3600 Вт • с = 3,6 • 10
3
Дж;
1 кВт
•
ч = 10
3
Вт
•
ч = 3,6
•
10° Дж.
Если ток проходит по неподвижно-
му металлическому проводнику, то вся
работа идет на его нагревание и, но за-
кону сохранения энергии,
dQ = dA. (99.4)
Таким образом, используя выраже-
ния (99.4), (99.1) и (99.2), получим
181

dQ =
IUdt
= PRdt =
—
dt.
(99.5)
R
Выражение (99.5) представляет со-
бой закон Джоуля
—Ленца,
экспери-
ментально установленный независимо
друг от друга Дж. Джоулем и Э. X. Лен-
цем
1
.
Выделим в проводнике элементар-
ный цилиндрический объем dV =
dSdl
(ось цилиндра совпадает с направлени-
ем тока), сопротивление которого R =
—
р—
. По закону Джоуля
—Ленца
за
dS
время
dt
в этом объеме выделится теп-
лота
dQ
-
PRdt =
= pj'Wd*.
Количество теплоты, выделяющее-
ся за единицу времени в единице объе-
ма, называется удельной тепловой
мощностью тока. Она равна
w
=
pf.
(99.6)
Используя дифференциальную фор-
му закона Ома (j —
^Е)
и соотношение
1
р — —, получим
w
=
jE
=
~iE
2
.
(99.7)
Формулы (99.6) и (99.7) являются
обобщенным выражением закона
Джоуля
—Ленца
в дифференциаль-
ной форме, пригодным для любого про-
водника.
Тепловое действие тока находит ши-
рокое применение в технике, которое
началось с открытия в 1873 г. русским
инженером А.Н.Лодыгиным (1847 —
1923) лампы накаливания.
На нагревании проводников элект-
рическим током основано действие
электрических муфельных печей, элек-
трической дуги [открыта русским ин-
женером В. В. Петровым (1761
—1834)],
контактной электросварки, бытовых
электронагревательных приборов и т. д.
§ 100. Закон Ома
для неоднородного участка цепи
Мы рассматривали закон Ома [см.
(98.1)] для однородного участка цепи,
т. е. такого, в котором не действует
ЭД
С
(не действуют сторонние силы). Теперь
рассмотрим неоднородный участок
цепи, где действующую ЭДС на участ-
ке 1 — 2 обозначим через
«?
12
,
а прило-
женную на концах участка разность
потенциалов — через
ф
х
—
ф
2
-
Если ток проходит по неподвижным
проводникам, образующим участок 1—2,
то работа
А
п
всех сил (сторонних и
электростатических), совершаемая над
носителями тока, по закону сохранения
и превращения энергии равна теплоте,
выделяющейся на участке. Работа сил,
совершаемая при перемещении заря-
да
Q
Q
на участке 1—2, согласно (97.4),
ЭДС
«Г
12
,
как и сила тока /, — вели-
чина скалярная. Ее необходимо брать
либо с положительным, либо с отрица-
тельным знаком в зависимости от зна-
ка работы, совершаемой сторонними
силами. Если ЭДС способствует движе-
нию положительных зарядов в выбран-
ном направлении (в направлении 1 — 2),
то
Ш"
12
> 0. Если
ЭДС
препятствует дви-
жению положительных зарядов в дан-
ном направлении, то
^
12
< 0.
За время t в проводнике выделяется
теплота [см. (99.5)]
Q =
pRt
= IR(It) =
IRQ
0
.
(100.2)
Из формул (100.1) и (100.2) полу-
чим
1
Э.Х.
Ленд (1804- 1865) - русский физик.
IR =
+
(100.3)
182
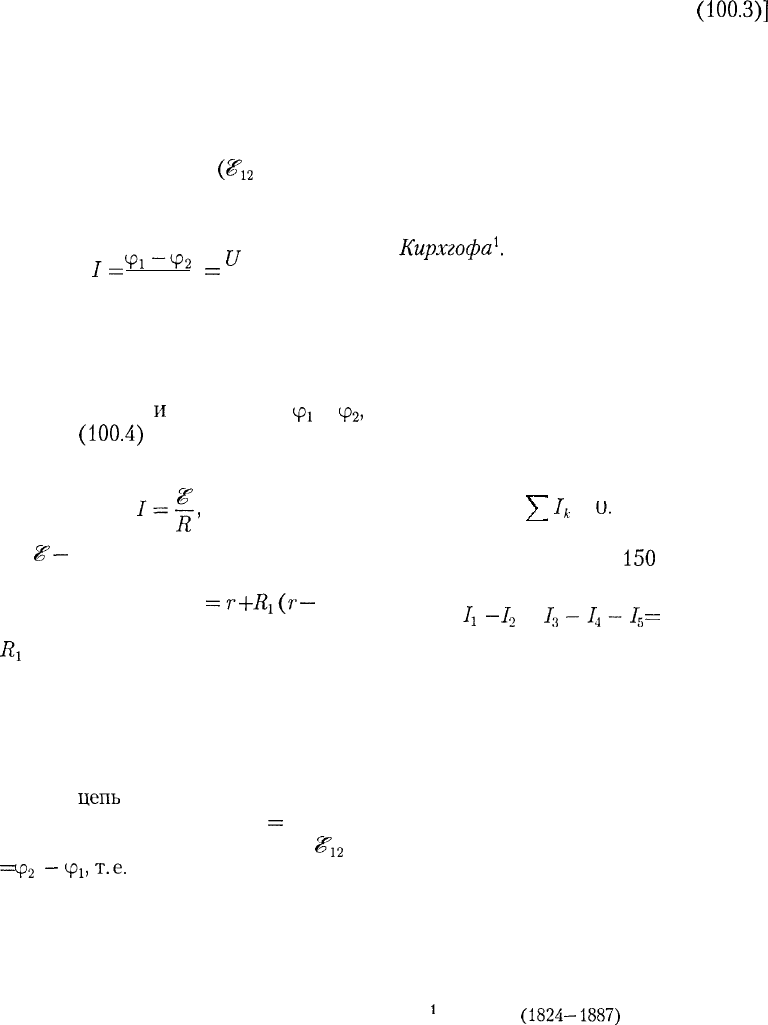
откуда
Выражение (100.3) или (100.4) пред-
ставляет собой закон Ома для неодно-
родного участка цепи в интегральной
форме, который является обобщенным
законом Ома.
Если на данном участке цепи источ-
ник тока отсутствует
(&
12
— 0), то из
(100.4) приходим к закону Ома для од-
нородного участка цепи (98.1):
/=
Ф1-Ф2
=
U
R R
[при отсутствии сторонних сил напря-
жение на концах участка равно разно-
сти потенциалов (см. § 97)]. Если же
электрическая цепь замкнута, то выб-
ранные точки 1
и
2 совпадают,
ф
х
=
ф
2
>
тогда из
(100.4)
получаем закон Ома для
замкнутой цепи:
/-£
R'
где
%—
ЭДС, действующая в цепи; R —
суммарное сопротивление всей цепи.
В общем случае R
—r+
R\(r—
внут-
реннее сопротивление источника тока,
R
x
— сопротивление внешней цепи).
Поэтому закон Ома для замкнутой цепи
будет иметь вид
Если
цепь
разомкнута и, следователь-
но, в ней ток отсутствует (/
=
0), то из
закона Ома (100.4) получим, что
*f
12
=
=
Фг
~
Фь
т
-
е
-
ЭДС, действующая в ра-
зомкнутой цепи, равна разности потен-
циалов на ее концах. Следовательно,
для того чтобы найти ЭДС источника
тока, надо измерить разность потенци-
алов на его клеммах при разомкнутой
цепи.
§ 101. Правила Кирхгофа
для разветвленных цепей
Обобщенный закон Ома [см.
(100.3)]
позволяет рассчитать практически лю-
бую сложную цепь. Однако непосред-
ственный расчет разветвленных цепей,
содержащих несколько замкнутых кон-
туров (контуры могут иметь общие уча-
стки, каждый из контуров может иметь
несколько источников тока и т.д.), до-
вольно сложен. Эта задача более про-
сто решается с помощью двух правил
Кирхгофа
1
.
Любая точка разветвления цепи, в
которой сходится не менее трех провод-
ников с током, называется узлом. При
этом ток, входящий в узел, считается
положительным, а ток, выходящий из
узла, — отрицательным.
Первое правило Кирхгофа: алгебра-
ическая сумма токов, сходящихся в
узле, равна нулю:
Е
т
— п
h
-
U.
к
Например, для рис.
150
первое пра-
вило Кирхгофа запишется так:
h
-
к
+
h
-/
4
-/
5
=
0.
Первое правило Кирхгофа вытекает
из закона сохранения электрического
заряда. Действительно, в случае устано-
вившегося постоянного тока ни в одной
точке проводника и ни на одном его
участке не должны накапливаться элек-
трические заряды. В противном случае
токи не могли бы оставаться постоян-
ными.
Второе правило Кирхгофа является
обобщением закона Ома для разветв-
ленных цепей. Рассмотрим контур, со-
стоящий из трех участков (рис. 151).
Направление обхода по часовой стрел-
1
Г. Кирхгоф
(1824
—1887)
— немецкий физик.
183

Рис. 150
Рис. 151
ке примем за положительное, отметив,
что выбор этого направления совершен-
но произволен. Все токи, совпадающие
по направлению с направлением обхо-
да контура, считаются положительны-
ми, не совпадающие с направлением
обхода — отрицательными. Источники
тока считаются положительными, если
они создают ток, направленный в сто-
рону обхода контура. Применяя к уча-
сткам закон Ома (100.3), можно запи-
сать:
Складывая почленно эти уравнения,
получим
I
X
R
X
-I
2
3
.
(101.1)
Уравнение
(101.1)
выражает второе
правило Кирхгофа: в любом замкну-
том контуре, произвольно выбранном
в разветвленной электрической цепи,
алгебраическая сумма произведений
сил токов /
г
на сопротивления
R
{
соот-
ветствующих участков этого контура
равна алгебраической сумме ЭДС
&
к
,
встречающихся в этом контуре:
При расчете сложных цепей посто-
янного тока с применением правил
Кирхгофа необходимо:
1. Выбрать произвольное направле-
ние токов на всех участках цепи; дей-
ствительное направление токов опреде-
лится при решении задачи: если иско-
мый ток получится положительным,
то
его направление было выбрано пра-
вильно, отрицательным — его истинное
направление противоположно выбран-
ному.
2. Выбрать направление обхода кон-
тура и строго его придерживаться; про-
изведение IR положительно, если ток
на данном участке совпадает с направ-
лением обхода, и, наоборот; ЭДС, дей-
ствующие по выбранному направлению
обхода, считаются положительными,
против — отрицательными.
3. Составить столько уравнений,
чтобы их число было равно числу
ис-
комых величин (в систему уравнений
должны входить все сопротивления и
ЭДС рассматриваемой цепи); каждый
рассматриваемый контур должен со-
держать хотя бы один элемент, не со-
держащийся в предыдущих контурах,
иначе получатся уравнения, являющи-
еся простой комбинацией уже состав-
ленных.
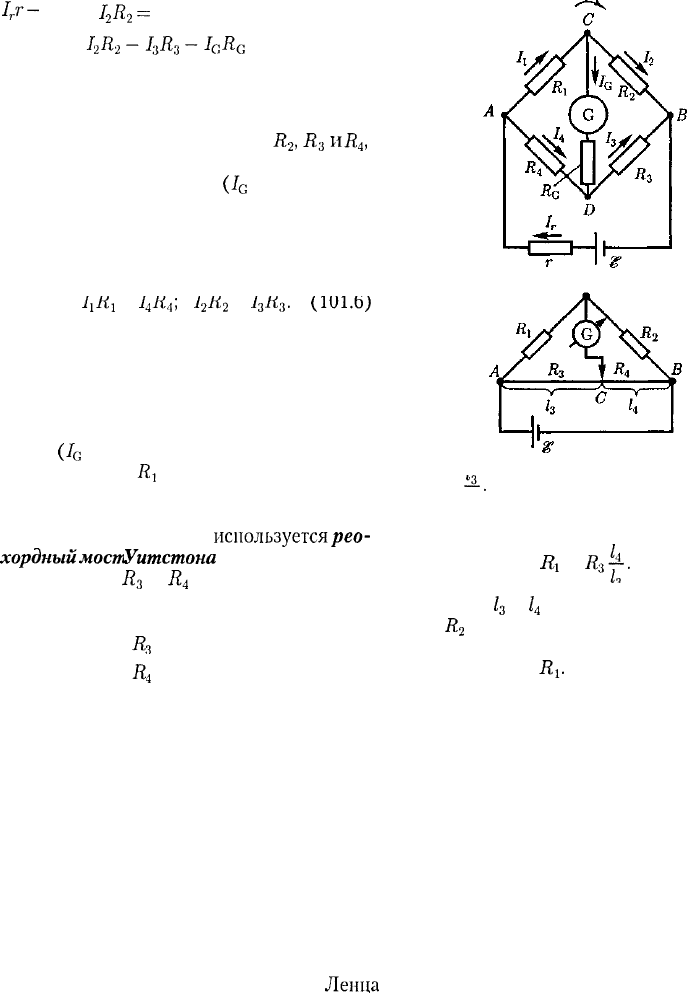
В качестве примера использования пра-
вил Кирхгофа рассмотрим схему (рис.
152)
измерительного
моста
УитстонаК
Сопро-
тивления
R
b
R
2
,
Л
3
и
R
4
образуют его «пле-
чи». Между точками Аи В моста включена
батарея с ЭДС
Ш'и
сопротивлением
г,
меж-
ду точками Си D включен гальванометр с
сопротивлением
R
G
.
Для узлов А, В и С,
применяя первое правило Кирхгофа, полу-
чим
b-b-Ic^O.
(101.3)
Для контуров А СВА, A
CD
А и CBDC, со-
гласно второму правилу Кирхгофа, можно
записать:
1
Ч.
Уитстон
(1802
—1875)
— английский фи-
зик.
184
i
r
r-
I
2
R
2
=
/
2
Д
2
-/3Д3
-/
G
/2
G
= 0. (101.4)
Если известны все сопротивления и
ЭДС, то, решая полученные шесть уравне-
ний, можно найти неизвестные токи. Изме-
няя известные сопротивления
R
2
,
i?
3
и
Я
4
,
можно добиться того, чтобы ток через галь-
ванометр был равен нулю
(7
G
= 0). Тогда из
(101.3) найдем
из (101.4) получим
1
1
к
1
—
1
А
к
А
, 1
2
к
2
—
1
3
щ.
(IUI.D;
Из (101.5) и (101.6) вытекает, что
•. (101.7)
Таким образом, в случае равновесного
моста
(I
G
= 0) при определении искомого
сопротивления
R
x
ЭДС батареи, сопротив-
ления батареи и гальванометра роли не иг-
рают.
На практике обычно
используетсярео-
хордныймост Уитстона (рис. 153), где со-
противления
R
3
и
R
A
представляют собой
длинную однородную проволоку (реохорд)
с большим удельным сопротивлением, так
Ri
что отношение —- можно заменить отноше-
R,
Рис. 152
Рис. 153
нием
-2-.
Тогда, используя выражение
ч
(101.7), можно записать
R
x
=
R,
l
f.
(101.8)
Длины /
3
и
1
А
легко измеряются по шка-
ле, a
R
2
всегда известно. Поэтому уравнение
(101.8) позволяет определить неизвестное
сопротивление
R
x
.
Контрольные вопросы
Что называют силой тока? плотностью тока? Каковы их единицы? Дать определения.
Назовите условия возникновения и существования электрического тока.
Что такое сторонние силы? Какова их природа?
В чем заключается физический смысл электродвижущей силы, действующей в цепи?
напряжения? разности потенциалов?
Почему напряжение является обобщенным понятием разности потенциалов?
Какова связь между сопротивлением и проводимостью, удельным сопротивлением и
удельной проводимостью?
В чем заключается явление сверхпроводимости? Каковы его перспективы?
На чем основано действие термометров сопротивления?
Выведите законы Ома и Джоуля —
Ленца
в дифференциальной форме.
В чем заключается физический смысл удельной тепловой мощности тока?
Проанализируйте обобщенный закон Ома. Какие частные законы можно из него полу-
чить?
Поясните физический смысл электродвижущей силы, разности потенциалов и напря-
жения на участке электрической цепи.
185

• Как формулируются правила Кирхгофа? На чем они основаны?
• Как составляются уравнения, выражающие правила Кирхгофа?
ЗАДАЧИ
12.1. По медному проводнику сечением 1 мм
2
течет ток; сила тока 1 А. Определите сред-
нюю скорость упорядоченного движения электронов вдоль проводника, предполагая, что
на каждый атом меди приходится один свободный электрон. Плотность меди 8,9 г/см
3
.
[74 мкм/с]
12.2. Определите, во сколько раз возрастет сила тока, проходящего через платиновую
печь, если при постоянном напряжении на зажимах ее температура повышается от
t
x
— 20 °С
до
t
2
— 1200 °С. Температурный коэффициент сопротивления платины принять равным
3,65
•
10"
3
К"
1
. [В 5 раз]
12.3. По медному проводу сечением 0,3 мм
2
течет ток 0,3 А. Определите силу, действую-
щую на отдельные свободные электроны со стороны электрического поля. Удельное сопро-
тивление меди 17 нОм • м. [2,72 •
10~
21
Н]
12.4. Сила тока в проводнике сопротивлением 10 Ом равномерно убывает от
/
0
=
3 А до
/ = 0 за 30 с. Определите выделившееся за это время в проводнике количество теплоты.
[900 Дж]
12.5. Плотность электрического тока в алюминиевом проводе равна 5 А/см
2
. Определи-
те удельную тепловую мощность тока, если удельное сопротивление алюминия 26 нОм • м.
[65Дж/(м
3
-с)]
12.6. Определите
внутреннее
сопротивление
г
источника тока, если во внешней цепи
при силе тока
1
г
— 5 А выделяется мощность
Р
х
= 10 Вт, а при силе тока
/
2
= 8 А мощность
Р
2
= 12 Вт. [0,17 Ом]
12.7. Три источника тока с ЭДС
%
х
= 1,8 В,
&
2
= 1,4 В и
«Г
3
=
1Д
В
соединены накоротко
одноименными полюсами. Внутреннее сопротивление первого источника
г
х
— 0,4 Ом, вто-
рого —
т
2
= 0,6 Ом. Определите внутреннее сопротивление третьего источника, если через
первый источник идет ток
1
г
= 1,13 А. [0,2 Ом]
Глава 13
ЭЛЕКТРИЧЕСКИЕ ТОКИ В МЕТАЛЛАХ,
ВАКУУМЕ И ГАЗАХ
§ 102. Элементарная
классическая теория
электропроводности металлов
Носителями тока в металлах явля-
ются свободные электроны, т. е. элект-
роны, слабо связанные с ионами крис-
таллической решетки металла. Это
представление о природе носителей
тока в металлах основывается на элек-
тронной теории проводимости ме-
таллов, созданной немецким физиком
П. Друде (1863 — 1906) и разработанной
впоследствии нидерландским физиком
X. Лоренцем, а также на ряде класси-
ческих опытов, подтверждающих поло-
жения электронной теории.
Первый из таких опытов — опыт
Рикке
1
(1901), в котором в течение года
1
К. Рикке (1845— 1915) — немецкий физик.
186

электрический ток пропускался через
три последовательно соединенных с
тщательно отшлифованными торцами
металлических цилиндра
(Си,
А1, Си)
одинакового радиуса. Несмотря на то
что общий заряд, прошедший через эти
цилиндры, достигал огромного значе-
нии
(«3,5
•
10
6
Кл), никаких, даже мик-
роскопических, следов переноса веще-
ства не обнаружилось. Это явилось
экспериментальным доказательством
того, что ионы в металлах не участву-
ют в переносе электричества, а перенос
заряда в металлах осуществляется час-
тицами, которые являются общими для
всех металлов. Такими частицами мог-
ли быть открытые в 1897 г. английским
физиком Д.Томсоном (1856 — 1940)
электроны.
Для доказательства этого предполо-
жения необходимо было определить
знак и величину удельного заряда но-
сителей (отношение заряда носителя к
его массе). Идея подобных опытов зак-
лючалась в следующем: если в металле
имеются подвижные, слабо связанные
с решеткой носители тока, то при рез-
ком торможении проводника эти части-
цы должны по инерции смещаться впе-
ред, как смещаются вперед пассажиры,
стоящие в вагоне при его торможении.
Результатом смещения зарядов должен
быть импульс тока; по направлению
тока можно определить знак носителей
тока, а зная размеры и сопротивление
проводника, можно вычислить удель-
ный заряд носителей.
Идея этих опытов (1913) и их каче-
ственное воплощение принадлежат
российским физикам С.Л.Мандельш-
таму (1879-1944) и Н.Д.Папалекси
(1880-1947). Эти опыты в 1916 г. были
усовершенствованы и проведены аме-
риканским физиком Р.Толменом
(1881 — 1948) и ранее шотландским
физиком Б.Стюартом (1828—1887).
Ими экспериментально доказано, что
носители тока в металлах имеют отри-
цательный заряд, а их удельный заряд
приблизительно одинаков для всех ис-
следованных металлов. По значению
удельного заряда носителей электри-
ческого тока и по определенному ранее
Р. Милликеном элементарному элект-
рическому заряду была определена их
масса. Оказалось, что значения удель-
ного заряда и массы носителей тока и
электронов, движущихся в вакууме, со-
впадали. Таким образом, было оконча-
тельно доказано, что носителями элек-
трического тока в металлах являются
свободные электроны.
Существование свободных электро-
нов в металлах можно объяснить сле-
дующим образом: при образовании кри-
сталлической решетки металла (в ре-
зультате сближения изолированных
атомов) валентные электроны, сравни-
тельно слабо связанные с атомными яд-
рами, отрываются от атомов металла,
становятся «свободными» и могут пе-
ремещаться по всему объему. Таким об-
разом, в узлах кристаллической решет-
ки располагаются ионы металла, а меж-
ду ними хаотически движутся свобод-
ные электроны, образуя своеобразный
электронный газ, обладающий, соглас-
но электронной теории металлов, свой-
ствами идеального газа.
Электроны проводимости при сво-
ем движении сталкиваются с ионами
решетки, в результате чего устанавли-
вается термодинамическое равновесие
между электронным газом и решеткой.
По теории Друде —Лоренца, электро-
ны обладают такой же энергией тепло-
вого движения, как и молекулы одно-
атомного газа. Поэтому, применяя вы-
воды молекулярно-кинетической тео-
рии [см. (44.3)], можно найти среднюю
скорость теплового движения электро-
нов
187
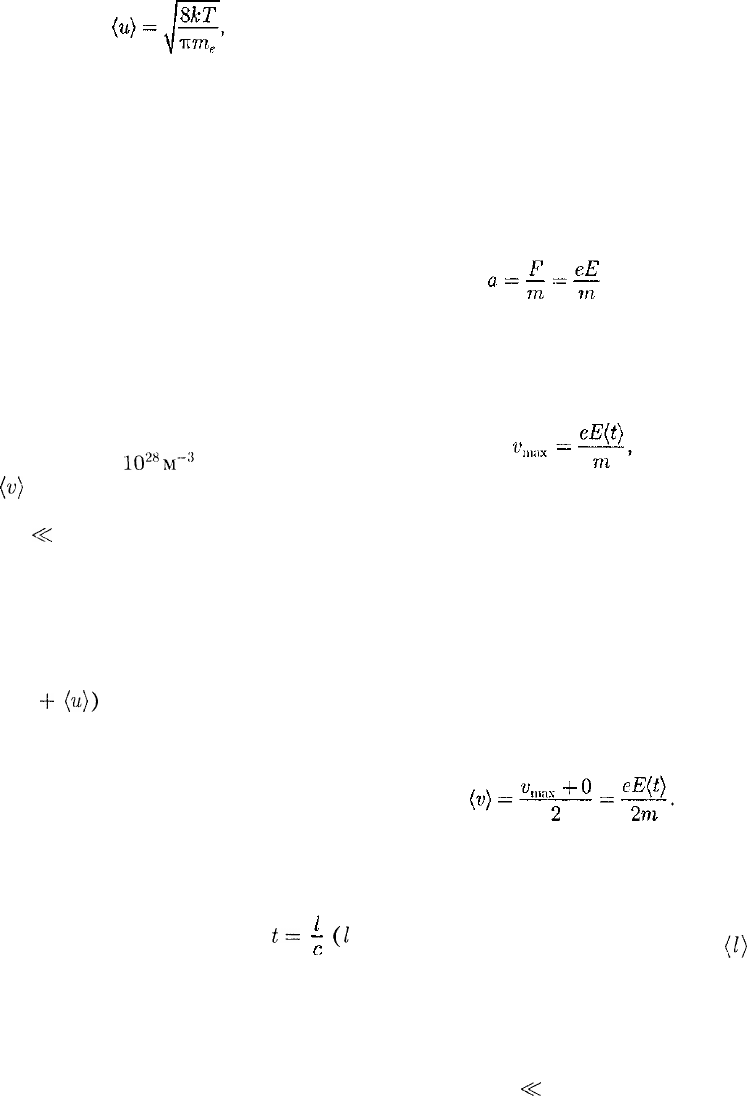
которая для Т— 300 К равна 1,1 • 10
5
м/с.
Тепловое движение электронов, явля-
ясь хаотическим, не может привести к
возникновению тока.
При наложении внешнего электри-
ческого поля на металлический провод-
ник кроме теплового движения элект-
ронов происходит их упорядоченное
движение, т. е. возникает электрический
ток. Среднюю скорость (v) упорядо-
ченного движения электронов можно
оценить согласно формуле (96.1) для
плотности тока: j = ne(v). Выбрав до-
пустимую плотность тока, например
для медных проводов 10
7
А/м
2
, полу-
чим, что при концентрации носителей
тока п = 8 •
10
28
м"
3
средняя скорость
(v)
упорядоченного движения электро-
нов равна 7,8 • 10~
4
м/с. Следовательно,
(v)
<C
{и), т.е. даже при очень больших
плотностях тока средняя скорость упо-
рядоченного движения электронов,
обусловливающего электрический ток,
значительно меньше их скорости теп-
лового движения. Поэтому при вы-
числениях результирующую скорость
((v)
+
{и))
можно заменять скоростью
теплового движения (и).
Казалось бы, полученный результат
противоречит факту практически
мгновенной передачи электрических
сигналов на большие расстояния. Дело
в том, что замыкание электрической
цепи влечет за собой распространение
электрического поля со скоростью с
(с = 3 • 10
8
м/с). Через время
t—
(I
—
длина цепи) вдоль цепи установится
стационарное электрическое поле и в
ней начнется упорядоченное движение
электронов. Поэтому электрический
ток возникает в цепи практически од-
новременно с ее замыканием.
§ 103. Вывод основных законов
электрического тока
в классической теории
проводимости металлов
1. Закон Ома. Пусть в металличе-
ском проводнике существует электри-
ческое поле напряженностью Е = const.
Со стороны поля заряд е испытывает
действие силы F= eЕ и приобретает ус-
корение
. Таким образом,
во время свободного пробега электро-
ны движутся равноускоренно, приобре-
тая к концу свободного пробега ско-
рость
где (t) — среднее время между двумя
последовательными соударениями элек-
трона с ионами решетки.
Согласно теории Друде, в конце сво-
бодного пробега электрон,сталкиваясь
с ионами решетки, отдает им накоплен-
ную в поле энергию, поэтому скорость
его упорядоченного движения стано-
вится равной нулю. Следовательно,
средняя скорость направленного дви-
жения электрона
(103.1)
Классическая теория металлов не
учитывает распределения электронов
по скоростям, поэтому среднее время (t)
свободного пробега определяется сред-
ней длиной свободного пробега
{/)
и
средней скоростью движения электро-
нов относительно кристаллической ре-
шетки проводника, равной (и) + (v)
({и} — средняя скорость теплового дви-
жения электронов). В § 102 было пока-
зано, что (v)
<C
(и), поэтому
188
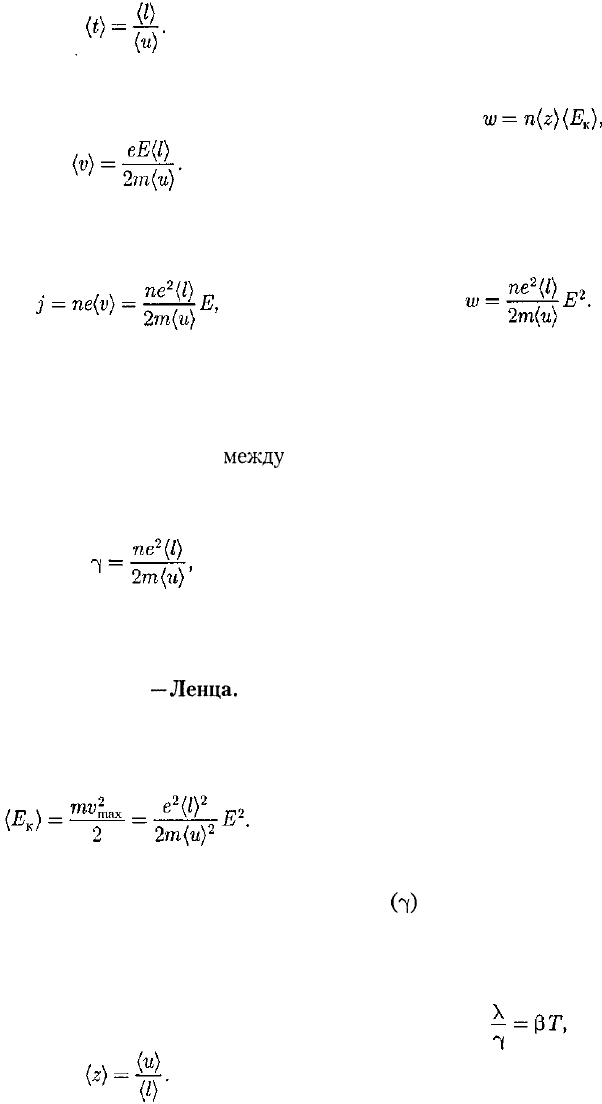
Подставив значение (t) в формулу
(103.1), получим
Плотность тока в металлическом
проводнике по (96.1)
откуда видно, что плотность тока про-
порциональна напряженности поля,
т.е. получили закон Ома в дифферен-
циальной форме [ср. с (98.4)]. Коэффи-
циент пропорциональности
между
j и Е
есть не что иное, как удельная прово-
димость материала
(103.2)
которая тем больше, чем больше кон-
центрация свободных электронов и
средняя длина их свободного пробега.
2. Закон Джоуля
—Ленца.
К концу
свободного пробега электрон под дей-
ствием поля приобретает дополнитель-
ную кинетическую энергию
(103.3)
При соударении электрона с ионом
эта энергия полностью передается ре-
шетке и идет на увеличение внутренней
энергии металла, т. е. на его нагревание.
За единицу времени электрон испы-
тывает с узлами решетки в среднем (z)
столкновений:
(103.4)
Если п — концентрация электронов,
то в единицу времени происходит n(z)
столкновений и решетке передается
энергия
(103.5)
которая идет на нагревание проводни-
ка. Подставив (103.3) и (103.4) в (103.5),
получим энергию, передаваемую ре-
шетке в единице объема проводника за
единицу времени,
(103.6)
Величина w является удельной теп-
ловой мощностью тока (см. § 99). Ко-
эффициент пропорциональности меж-
ду w и Е
2
по (103.2) есть удельная про-
водимость % следовательно, выражение
(103.6) — закон Джоуля — Ленца в диф-
ференциальной форме [ср. с (99.7)].
3. Закон Видемана —Франца. Ме-
таллы обладают как большой электри-
ческой проводимостью, так и высокой
теплопроводностью. Это объясняется
тем, что носителями тока и теплоты в
металлах являются одни и те же части-
цы — свободные электроны, которые,
перемещаясь в металле, переносят не
только электрический заряд, но и при-
сущую им энергию хаотического (теп-
лового) движения, т.е. осуществляют
перенос теплоты.
Видеманом и Францем в 1853 г. экс-
периментально установлен закон, со-
гласно которому отношение теплопро-
водности (X) к удельной проводимос-
ти
(ч)
для всех металлов при одной и
той же температуре одинаково и увели-
чивается пропорционально термодина-
мической температуре:
где (3 — постоянная, не зависящая от
рода металла.
189

Элементарная классическая теория
электропроводности металлов позво-
лила найти значение где
к — постоянная Больцмана. Это значе-
ние хорошо согласуется с опытными
данными. Однако, как оказалось впос-
ледствии, это согласие теоретического
значения с опытным случайно. Лоренц,
применив к электронному газу статис-
тику Максвелла — Больцмана, учтя тем
самым распределение электронов по
скоростям, получил что при-
вело к резкому расхождению теории с
опытом.
Таким образом, классическая теория
электропроводности металлов объяс-
нила законы Ома и Джоуля — Ленца, а
также дала качественное объяснение
закона Видемана — Франца. Однако она
помимо рассмотренных противоречий
в законе Видемана — Франца столкну-
лась еще с рядом трудностей при объяс-
нении различных опытных данных.
Рассмотрим некоторые из них.
Температурная зависимость сопро-
тивления. Из формулы удельной про-
водимости (103.2) следует, что сопро-
тивление металлов, т.е. величина, об-
ратно пропорциональная
%
должна воз-
растать пропорционально
л/г
[в (103.2)
пи
{/)
от температуры не зависят, а
(и)
~
л/г]. Этот вывод электронной те-
ории противоречит опытным данным,
согласно которым R
~
Г (см. § 98).
Оценка средней длины свободного
пробега электронов в металлах. Что-
бы по формуле (103.2) получить
%
со-
впадающие с опытными значениями,
надо принимать
(/)
значительно боль-
ше истинных, иными словами, предпо-
лагать, что электрон проходит без со-
ударений с ионами решетки сотни меж-
доузельных расстояний, что не согласу-
ется с теорией Друде — Лоренца.
Теплоемкость металлов. Теплоем-
кость металла складывается из тепло-
емкости его кристаллической решетки
и теплоемкости электронного газа. По-
этому атомная (т.е. рассчитанная на
1 моль) теплоемкость металла должна
быть значительно больше атомной теп-
лоемкости диэлектриков, у которых нет
свободных электронов. Согласно зако-
ну Дюлонга и Пти (см. § 73), теплоем-
кость одноатомного кристалла равна
3R. Учтем, что теплоемкость одноатом-
ного электронного газа равна
3
/2-R.
Тогда атомная теплоемкость металлов
должна быть близка к
4,5R.
Однако
опыт доказывает, что она равна
3R,
т. е.
для металлов, так же как и для диэлек-
триков, хорошо выполняется закон
Дюлонга и Пти. Следовательно, нали-
чие электронов проводимости практи-
чески не сказывается на значении теп-
лоемкости, что не объясняется класси-
ческой электронной теорией.
Указанные расхождения теории
с опытом можно объяснить тем, что
движение электронов в металлах под-
чиняется не законам классической ме-
ханики, а законам квантовой механики
и, следовательно, поведение электро-
нов проводимости надо описывать не
статистикой Максвелла — Больцмана,
а квантовой статистикой. Поэтому
объяснить затруднения элементарной
классической теории электропроводно-
сти металлов можно лишь квантовой
теорией, которая будет рассмотрена в
дальнейшем. Надо, однако, отметить,
что классическая электронная теория
не утратила своего значения и до насто-
ящего времени, так как во многих слу-
чаях (например, при малой концентра-
ции электронов проводимости и высо-
кой температуре) она дает правильные
качественные результаты и является по
сравнению с квантовой теорией про-
стой и наглядной.
190
