Torrieri D. Principles of Spread-Spectrum Communication Systems
Подождите немного. Документ загружается.

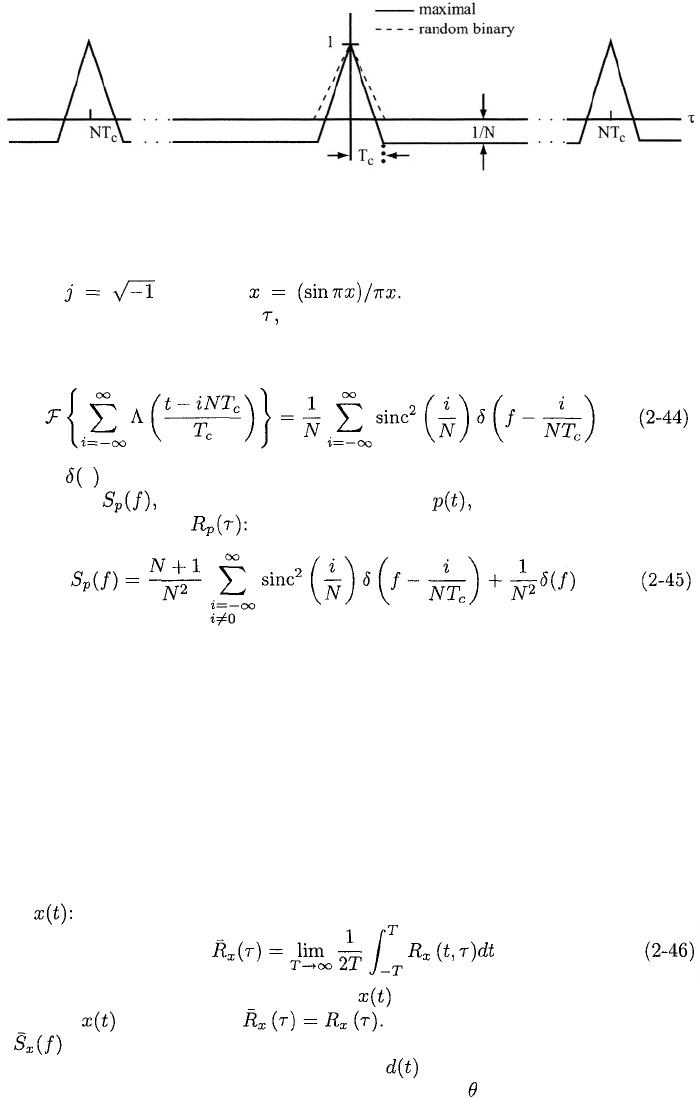
68
CHAPTER 2.
DIRECT-SEQUENCE SYSTEMS
Figure 2.9: Autocorrelations of maximal sequence and random binary sequence.
where
and sinc
Since the infinite series in (2-
42) is a periodic function of it can be expressed as a complex exponential
Fourier series. From (2-43) and the fact that the Fourier transform of a complex
exponential is a delta function, we obtain
where is the Dirac delta function. Applying this identity to (2-42), we
determine the power spectral density of which is defined as the
Fourier transform of
This function, which consists of an infinite series of delta functions, is depicted
in Figure 2.10.
A pseudonoise or pseudorandom sequence is a periodic binary sequence with
a nearly even balance of 0’s and 1’s and an autocorrelation that roughly re-
sembles, over one period, the autocorrelation of a random binary sequence.
Pseudonoise sequences, which include the maximal sequences, provide practi-
cal spreading sequences because their autocorrelations facilitate code synchro-
nization in the receiver (Chapter 4). Other sequences have peaks that hinder
synchronization.
To derive the power spectral density of a direct-sequence signal with a pe-
riodic spreading sequence, it is necessary to define the average autocorrelation
of
The limit exists and may be nonzero if has finite power and infinite dura-
tion. If is stationary, The average power spectral density
is defined as the Fourier transform of the average autocorrelation.
For the direct-sequence signal of (2-1), is modeled as a random binary
sequence with autocorrelation given by (2-13), and is modeled as a random
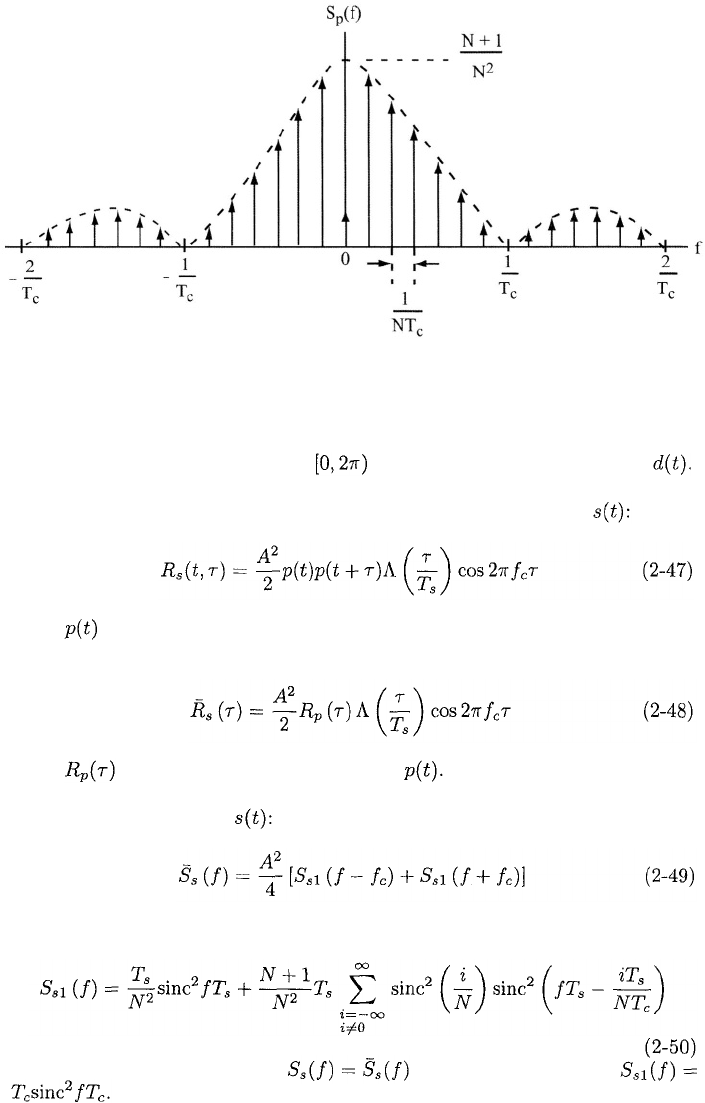
2.2.
SPREADING SEQUENCES AND WAVEFORMS
69
Figure 2.10: Power spectral density of maximal sequence.
variable uniformly distributed over and statistically independent of
Neglecting the constraint that the bit transitions must coincide with chip tran-
sitions, we obtain the autocorrelation of the direct-sequence signal
where is the periodic spreading waveform. Substituting this equation into
(2-46) and using (2-36), we obtain
where is the periodic autocorrelation of For a maximal spreading se-
quence, the convolution theorem, (2-48), (2-43), and (2-45) provide the average
power spectral density of
where the lowpass equivalent density is
For a random binary sequence, is given by (2-49) with

70
CHAPTER 2.
DIRECT-SEQUENCE SYSTEMS
Polynomials over the Binary Field
Polynomials allow a compact description of the dependence of the output se-
quence of a linear feedback shift register on its feedback coefficients and initial
state. A polynomial over the binary field
GF
(2) has the form
where the coefficients
are elements of GF
(2)
and the symbol
is an indeterminate introduced for convenience in calculations. The degree of
a polynomial is the largest power of with a nonzero coefficient. The sum of
a polynomial of degree and a polynomial of degree is another
polynomial over GF
(2)
defined as
where denotes the larger of and An example is
The product of two polynomials over GF(2) is another polynomial over GF
(1)
defined as
where the inner addition is modulo 2. For example,
It is easily verified that associative, commutative, and distributive laws apply
to polynomial addition and multiplication.
The characteristic polynomial associated with a linear feedback shift register
of stages is defined as
where assuming that stage contributes to the generation of the
output sequence. The generating function associated with the output sequence
is defined as
2.2.
SPREADING SEQUENCES AND WAVEFORMS
71
Substitution of (2-20) into this equation yields
Combining this equation with (2-56), and defining
we obtain
which implies that
Thus, the generating function of the output sequence generated by a linear
feedback shift register with characteristic polynomial may be expressed in
the form where the degree of is less than the degree
of The output sequence is said to be generated
by
Equation (2-
60) explicitly shows that the output sequence is completely determined by the
feedback coefficients and the initial state
In Figure 2.6, the feedback coefficients are and and
the initial state gives and Therefore,
Performing the long polynomial division according to the rules of binary arith-
metic yields which implies the output sequence
listed in the figure.
The polynomial is said to divide the polynomial if there is a poly-
nomial such that A polynomial over
GF
(2) of degree
is called irreducible if is not divisible by any polynomial over GF
(2)
of
72
CHAPTER 2.
DIRECT-SEQUENCE SYSTEMS
degree less than but greater than zero. If is irreducible over GF(
2
),
then for otherwise would divide If has an even number
of terms, then and the fundamental theorem of algebra implies that
divides Therefore, an irreducible polynomial over GF(2) must have
an odd number of terms, but this condition is not sufficient for irreducibility.
For example, is irreducible, but
is
not.
If a shift-register sequence is periodic with period then its generating
function may be expressed as
where is a polynomial of degree Therefore,
Suppose that and have no common factors, which is true if is
irreducible since is of lower degree than Then must divide
Conversely, if the characteristic polynomial divides then
for some polynomial and
which has the form of (2-62). Thus, generates a sequence of period for
all and, hence, all initial states.
A polynomial over GF
(2)
of degree
is called primitive if the smallest
positive integer for which the polynomial divides is
Thus, a primitive characteristic polynomial of degree can generate a sequence
of period which is the period of a maximal sequence generated by a
characteristic polynomial of degree Suppose that a primitive characteristic
polynomial of positive degree could be factored so that
where is of positive degree and is of positive degree A
partial-fraction expansion yields
Since and can serve as characteristic polynomials, the period of the
first term in the expansion cannot exceed while the period of the second
term cannot exceed Therefore, the period of cannot exceed

2.2.
SPREADING SEQUENCES AND WAVEFORMS
73
, which contradicts the assumption that
is primitive. Thus, a primitive characteristic polynomial must be irreducible.
Theorem.
A characteristic polynomial of degree
generates a maximal
sequence of period
if and only if it is a primitive polynomial.
Proof: To prove sufficiency, we observe that if is a primitive charac-
teristic polynomial, it divides for so a maximal sequence of
period is generated. If a sequence of smaller period could be generated,
then the irreducible would have to divide for which contra-
dicts the assumption of a primitive polynomial. To prove necessity, we observe
that if the characteristic polynomial generates a maximal sequence with
period then cannot divide because a sequence
with a smaller period would result, and such a sequence cannot be generated
by a maximal sequence generator. Since does divide it must be a
primitive polynomial.
Primitive polynomials are difficult to find, but many have been tabulated
(e.g., [4]). Those for which and one of those of minimal coefficient weight
for are listed in Table 2.1 as octal numbers in increasing order (e.g.,
For any positive integer the number of
different primitive polynomials of degree over GF(
2
) is
where the Euler function is the number of positive integers that are less
than and relatively prime to the positive integer If is a prime number,
74
CHAPTER 2.
DIRECT-SEQUENCE SYSTEMS
In general,
where are the prime integers that divide Thus,
and
Long Nonlinear Sequences
A long sequence or long code is a spreading sequence with a period that is much
longer than the data-symbol duration and may even exceed the message du-
ration. A short sequence or short code is a spreading sequence with a period
that is equal to or less than the data-symbol duration. Since short sequences
are susceptible to interception and linear sequences are inherently suscepti-
ble to mathematical cryptanalysis [1], long nonlinear pseudonoise sequences
and programmable code generators are needed for communications with a high
level of security. However, if a modest level of security is acceptable, short
or moderate-length pseudonoise sequences are preferable for rapid acquisition,
burst communications, and multiuser detection.
The algebraic structure of linear feedback shift registers makes them sus-
ceptible to cryptanalysis. Let
denote the column vector of the feedback coefficients of an linear
feedback shift register, where T denotes the transpose. The column vector of
successive sequence bits produced by the shift register starting at bit is
Let denote the matrix with columns consisting of the vectors
for
The linear recurrence relation (2-14) indicates that the output sequence and
feedback coefficients are related by
If consecutive sequence bits are known, then and are completely
known for some If is invertible, then the feedback coefficients can be
computed from
2.2.
SPREADING SEQUENCES AND WAVEFORMS
75
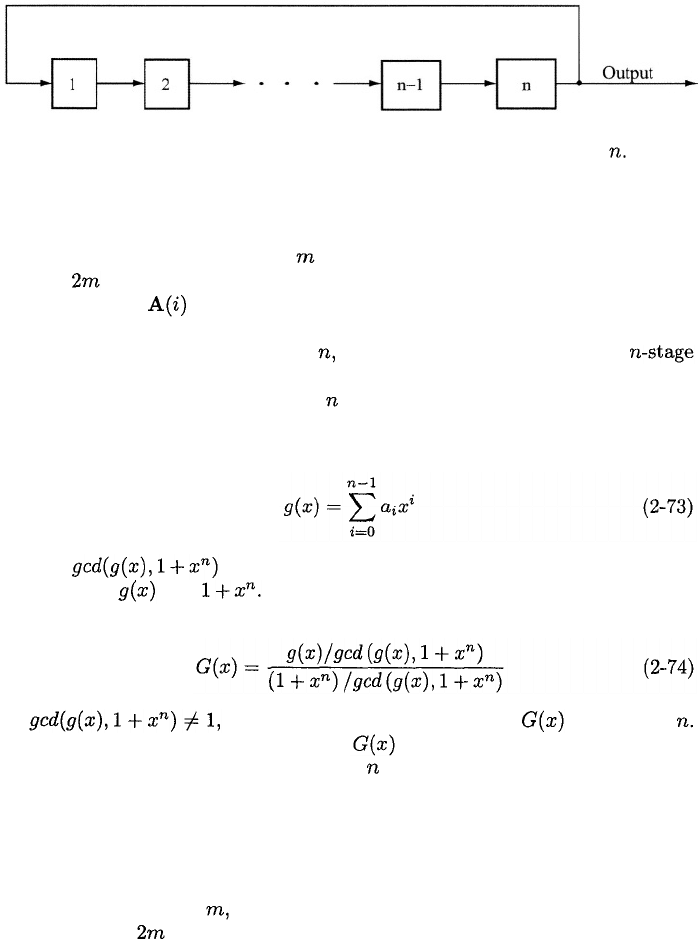
Figure 2.11: Linear generator of binary sequence with period
A shift-register sequence is completely determined by the feedback coefficients
and any state vector. Since any successive sequence bits determine a state
vector, successive bits provide enough information to reproduce the output
sequence unless is not invertible. In that case, one or more additional bits
are required.
If a binary sequence has period it can always be generated by a
linear feedback shift register by connecting the output of the last stage to the
input of the first stage and inserting consecutive bits of the sequence into the
output sequence, as illustrated in Figure 2.11. The polynomial associated with
one period of the binary sequence is
Let denote the greatest common polynomial divisor of the
polynomials and Then (2-62) implies that the generating function
of the sequence may be expressed as
If the degree of the denominator of is less than
Therefore, the sequence represented by can be generated by a linear feed-
back shift register with fewer stages than and with the characteristic function
given by the denominator. The appropriate initial state can be determined from
the coefficients of the numerator.
The linear equivalent of the generator of a sequence is the linear shift register
with the fewest stages that produces the sequence. The number of stages in the
linear equivalent is called the linear complexity of the sequence. If the linear
complexity is equal to then (2-72) determines the linear equivalent after the
observation of consecutive sequence bits. Security improves as the period of
a sequence increases, but there are practical limits to the number of shift-register
stages. To produce sequences with a long enough period for high security, the
feedback logic in Figure 2.5 must be nonlinear. Alternatively, one or more
shift-register sequences or several outputs of shift-register stages may be applied
to a nonlinear device to produce the sequence [5]. Nonlinear generators with
relatively few shift-register stages can produce sequences of enormous linear
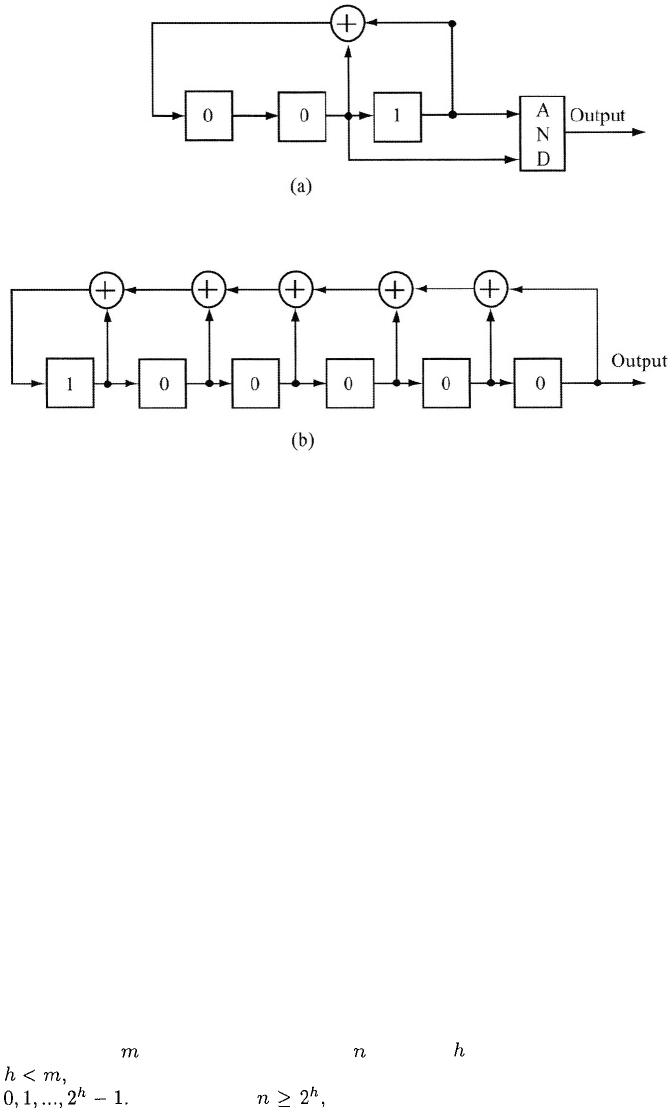
complexity. As an example, Figure 2.12(a) depicts a nonlinear generator in
76
CHAPTER 2.
DIRECT-SEQUENCE SYSTEMS
Figure 2.12: (a) Nonlinear generator and (b) its linear equivalent.
which two stages of a linear feedback shift register have their outputs applied
to an AND gate to produce the output sequence. The initial contents of the
shift-register stages are indicated by the enclosed binary numbers. Since the
linear generator produces a maximal sequence of length 7, the output sequence
has period 7. The first period of the sequence is (0 0 0 0 0 1 1), from which the
linear equivalent with the initial contents shown in Figure 2.12(b) is derived by
evaluating (2-74).
While a large linear complexity is necessary for the cryptographic integrity
of a sequence, it is not necessarily sufficient because other statistical charac-
teristics, such as a nearly even distribution of 1’s and 0’s, are required. For
example, a long sequence of many 0’s followed by a single 1 has a linear com-
plexity equal to the length of the sequence, but the sequence is very weak. The
generator of Figure 2.12(a) produces a relatively large number of 0’s because
the AND gate produces a 1 only if both of its inputs are 1’s.
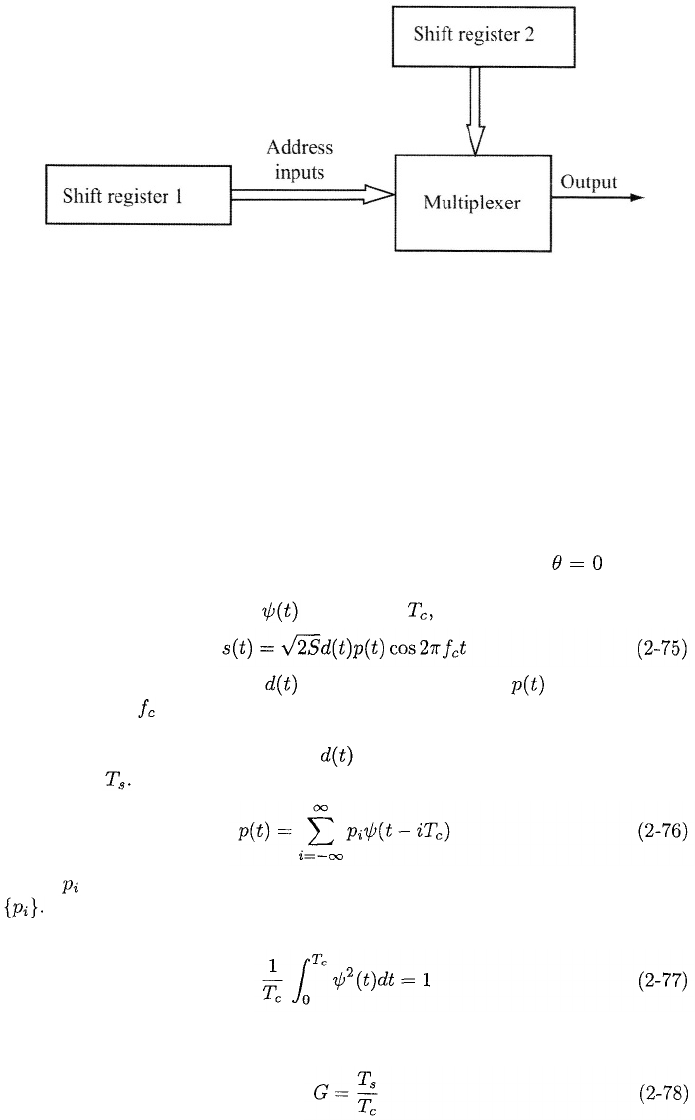
As another example, a nonlinear generator that uses a multiplexer is shown
in Figure 2.13. The outputs of various stages of feedback shift register 1 are
applied to the multiplexer, which interprets the binary number determined
by these outputs as an address. The multiplexer uses this address to select
one of the stages of feedback shift register 2. The selected stage provides the
multiplexer output and, hence, one bit of the output sequence. Suppose that
register 1 has stages and register 2 has stages. If stages of register 1, where
are applied to the multiplexer, then the address is one of the numbers
Therefore, if each address specifies a distinct stage of
2.3.
SYSTEMS WITH PSK MODULATION
77
Figure 2.13: Nonlinear generator that uses a multiplexer.
register 2. The initial states of the two registers, the feedback connections,
and which stages are used for addressing may be parts of a variable key that
provides security. The security of the nonlinear generator is further enhanced
if nonlinear feedback is used in both shift registers.
2.3 Systems with PSK Modulation
A received direct-sequence signal with coherent PSK modulation and ideal car-
rier synchronization can be represented by (2-1) or (2-6) with to reflect
the absence of phase uncertainty. Assuming that the chip waveform is well
approximated by a waveform of duration the received signal is
where S is the average power, is the data modulation, is the spreading
waveform, and is the carrier frequency. The data modulation is a sequence
of nonoverlapping rectangular chip waveforms, each of which has an amplitude
equal to +1 or –1. Each pulse of represents a data symbol and has a
duration of The spreading waveform has the form
where is equal to +1 or –1 and represents one chip of a spreading sequence
It is convenient, and entails no loss of generality, to normalize the energy
content of the chip waveform according to
Because the transitions of a data symbol and the chips coincide on both sides
of a symbol, the processing gain, defined as
