Torrieri D. Principles of Spread-Spectrum Communication Systems
Подождите немного. Документ загружается.

18
CHAPTER 1. CHANNEL CODES
are used. For the binary channel symbols, (1-34) and the lower bound in (1-33)
are used. For the chosen values of the best performance at is
obtained if the code rate is Further gains result from increasing
and hence the implementation complexity. Although the figure indicates the
performance advantage of Reed-Solomon codes with MFSK, there is a major
bandwidth penalty. Let B denote the bandwidth required for an uncoded bi-
nary PSK signal. If the same data rate is accommodated by using uncoded
binary frequeny-shift keying (FSK), the required bandwidth for demodulation
with envelope detectors is approximately 2B. For uncoded MFSK using
frequencies, the required bandwidth is because each symbol represents
bits. If a Reed-Solomon code is used with MFSK, the required band-
width becomes
Code Metrics for Orthogonal Signals
For orthogonal symbol waveforms, matched filters
are needed, and the observation vector is where each is
an row vector of matched-filter output samples for filter with
components
Suppose that symbol
of codeword uses unit-
energy waveform where the integer is a function of and If codeword
is transmitted over the AWGN channel, the received signal for symbol can
be expressed in complex notation as
where is independent, zero-mean, white Gaussian noise with two-sided
power spectral density is the carrier frequency, and is the phase.
Since the symbol energy for all the waveforms is unity,
The orthogonality of symbol waveforms implies that
A frequency translation or downconversion to baseband is followed by matched
filtering. Matched-filter which is matched to produces the output
samples
The substitution of (1-50) into (1-53), (1-52), and the assumption that each of
the has a spectrum confined to yields
1.1. BLOCK CODES
19
where if and otherwise, and
Since the real and imaginary components of are jointly Gaussian, this
random process is a
complex-valued Gaussian random variable.
Straightforward
calculations using (1-40) and the confined spectra of the indicates that
the real and are imaginary components of are uncorrelated and, hence,
independent and have the same variance Since the density of a complex-
valued random variable is defined to be the joint density of its real and imaginary
parts, the conditional probability density function of given is
The independence of the white Gaussian the orthogonality condition
(1-52)
,
and the spectrally confined symbol waveforms ensure that both the real
and imaginary parts of are independent of both the real and imaginary parts
of unless and Thus, the likelihood function of the observation
vector
y
is the product of the densities specified by (1-56).
For
coherent
signals, the are tracked by the phase synchronization sys-
tem and, thus, ideally may be set to zero. Forming the log-likelihood function
with the set to zero, and eliminating irrelevant terms that are independent
of we obtain the maximum-likelihood metric
where is the sampled output of the filter matched to the signal
representing symbol of codeword If each then the maximum-
likelihood metric is
and the common value does not need to be known to apply this metric.
For
noncoherent
signals, it is assumed that each is independent and uni-
formly distributed over which preserves the independence of the
Expanding the argument of the exponential function in (1-56), expressing in
polar form, and integrating over we obtain the probability density function
20
CHAPTER 1.
CHANNEL CODES
where is the modified Bessel function of the first kind and order zero, This
function may be represented by
Let denote the sampled envelope produced by the filter matched to
the signal representing symbol
of codeword
We form the log-likelihood
function and eliminate terms and factors that do not depend on the codeword
thereby obtaining the maximum-likelihood metric
If each then the maximum-likelihood metric is
and must be known to apply this metric.
From the series representation of it follows that
From the integral representation, we obtain
The upper bound in (1-63) is tighter for while the upper bound in
(1-64) is tighter for If we assume that is often less than 2,
then the approximation of by is reasonable. Substitution into
(1-61) and dropping an irrelevant constant gives the metric
If each then the value of is irrelevant, and we obtain the
Rayleigh
metric
which is suboptimal for the AWGN channel but is the maximum-likelihood
metric for the Rayleigh fading channel with identical statistics for each of the
symbols (Section 5.6). Similarly, (1-64) can be used to obtain suboptimal met-
rics suitable for large values of
1.1.
BLOCK CODES
21
To determine the maximum-likelihood metric for making a hard decision
on each symbol, we set and drop the subscript in (1-57) and (1-61).
We find that the maximum-likelihood symbol metric is for coherent
MFSK and for noncoherent MFSK, where the index ranges
over the symbol alphabet. Since the latter function increases monotonically
and is a constant, optimal symbol metrics or decision variables for
noncoherent MFSK are or for
Metrics and Error Probabilities for MFSK Symbols
For noncoherent MFSK, baseband matched-filter is matched to the unit-energy
waveform where If is the
received signal, a downconversion to baseband and a parallel set of matched
filters and envelope detectors provide the decision variables
The orthogonality condition (1-52) is satisfied if the adjacent frequencies are
separated by where is a nonzero integer. Expanding (1-67), we obtain
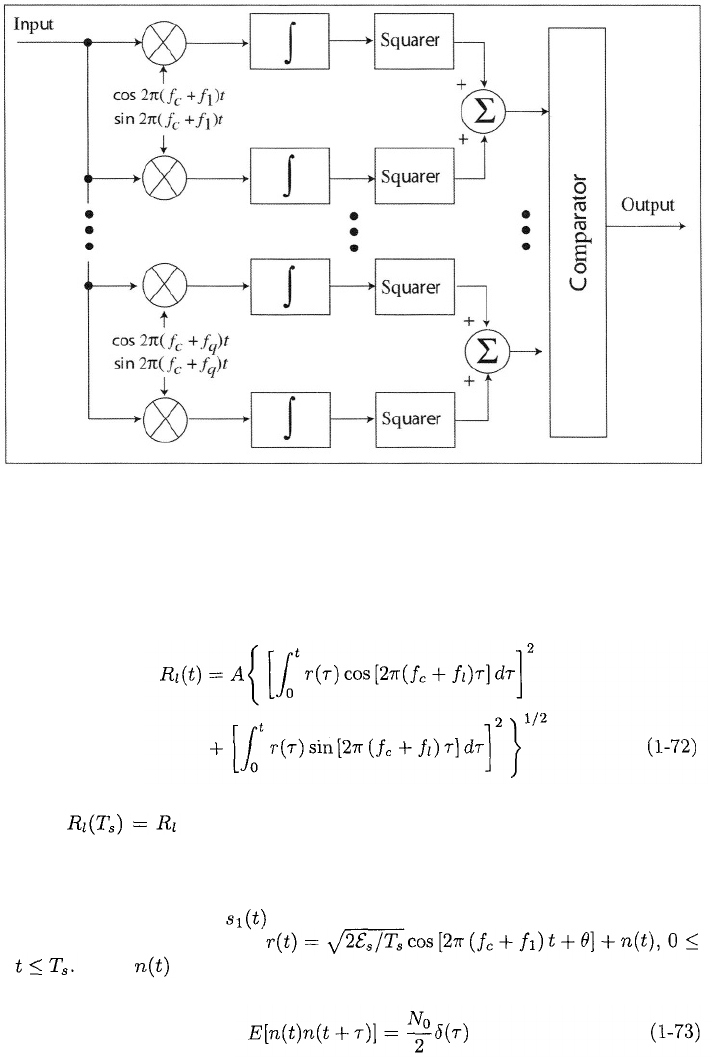
These equations imply the correlator structure depicted in Figure 1.4, where the
irrelevan
t
constant A has been omitted. The comparator decides what symbol
was transmitted by observing which comparator input is the largest.
To derive an alternative implementation, we observe that when the waveform
is the impulse response of a filter matched
to it is Therefore, the matched-filter output
at time is
22
CHAPTER 1.
CHANNEL CODES
Figure 1.4: Noncoherent MFSK receiver using correlators.
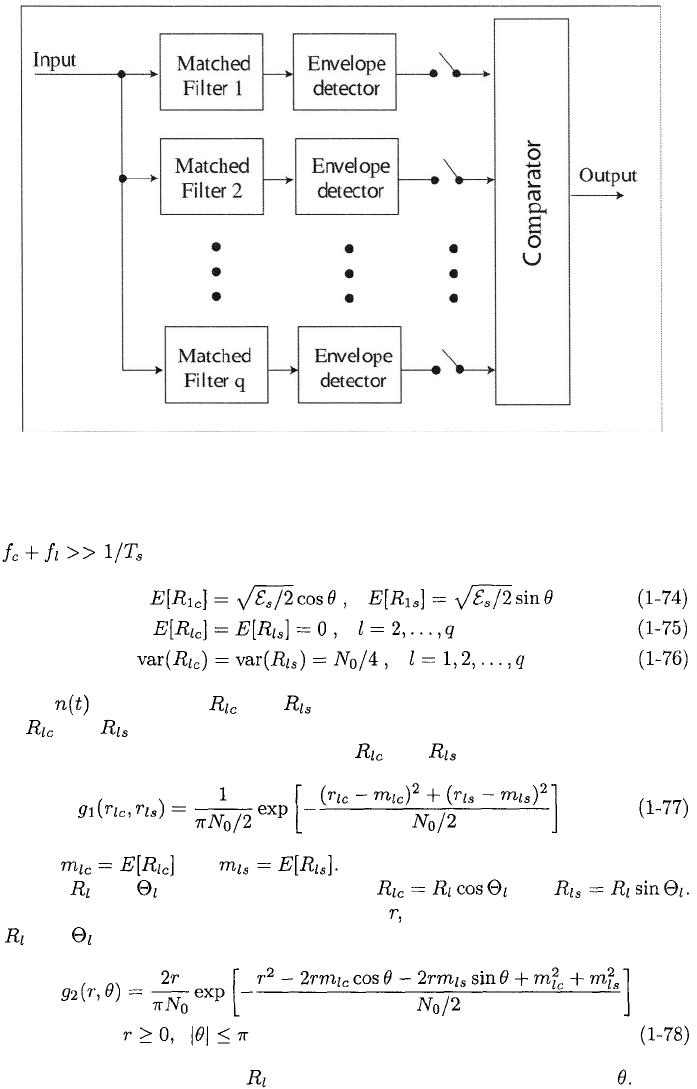
where the envelope is
Since given by (1-68), we obtain the receiver structure depicted
in Figure 1.5, where the irrelevant constant
A
has been omitted. A practical
envelope detector consists of a peak detector followed by a lowpass filter.
To derive the symbol error probability for equally likely MFSK symbols, we
assume that the signal was transmitted over the AWGN channel. The
received signal has the form
Since is white,
Using the orthogonality of the symbol waveforms and (1-73) and assuming that
1.1.
BLOCK CODES
23
Figure 1.5: Noncoherent MFSK receiver with passband matched filters.
in (1-69) and (1-70), we obtain
Since is Gaussian, and are jointly Gaussian. Since the covariance
of and is zero, they are mutually statistically independent. Therefore,
the joint probability density function of and is
where and
Let and be implicitly defined by and
Since the Jacobian of the transformation is we find that the joint density of
and
is
The density of the envelope is obtained by integration of (1-78) over Using
trigonometry and the integral representation of the Bessel function, we obtain
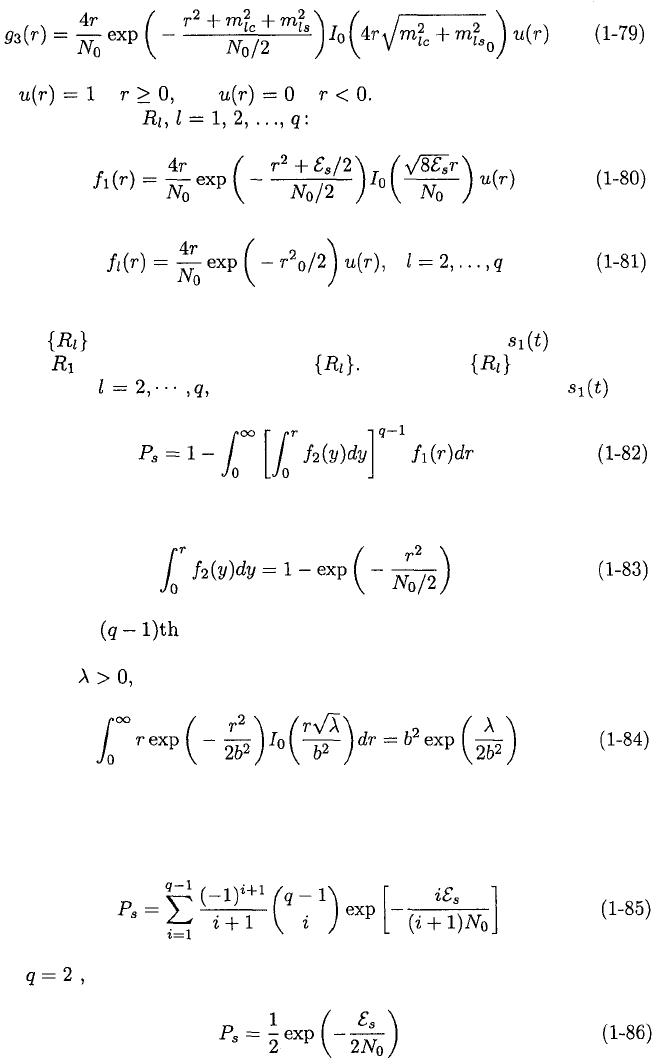
24
CHAPTER 1. CHANNEL CODES
the density
where if and if Substituting (1-74), we obtain
the densities for the
The orthogonality of the symbol waveforms and (1-73) imply that the random
variables are independent. A symbol error occurs when was trans-
mitted if is not the largest of the Since the are identically
distributed for the probability of a symbol error when was
transmitted is
Substituting (1-81) into the inner integral gives
Expressing the power of this result as a binomial expansion and then
substituting into (1-82), the remaining integration may be done by using the
fact that for
which follows from the fact that the density in (1-80) must integrate to unity.
The final result is the symbol error probability for noncoherent MFSK over the
AWGN channel:
When this equation reduces to the classical formula for binary FSK:

1.1.
BLOCK CODES
25
Chernoff Bound
The Chernoff bound is an upper bound on the probability that a random vari-
able equals or exceeds a constant. The usefulness of the Chernoff bound stems
from the fact that it is often much more easily evaluated than the probability
it bounds. The
moment generating function
of the random variable
X
with
distribution function is defined as
for all real-valued for which the integral is finite. For all nonnegative the
probability that is
Thus,
where is the upper limit of an open interval in which is defined. To
make this bound as tight as possible, we choose the value of that minimizes
Therefore,
which indicates the upper bound called the
Chernoff bound.
From (1-90) and
(1-87), we obtain the generalization
Since the moment generating function is finite in some neighborhood of
we may differentiate under the integral sign in (1-87) to obtain the derivative
of The result is
which implies that Differentiating (1-92) gives the second deriv-
ative
which implies that Consequently, is convex in its interval of
definition. Consider a random variable is such that
The first inequality implies that and the second inequality implies
that as Thus, since
the convex function
has a minimum value that is less than unity at some positive We
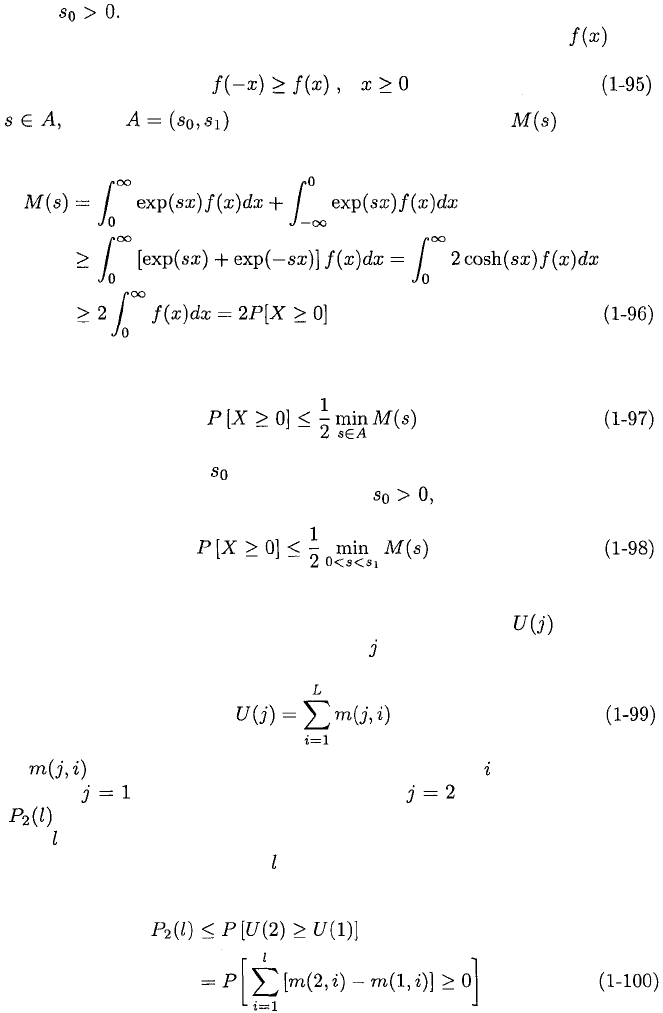
26
CHAPTER 1.
CHANNEL CODES
conclude that (1-94) is sufficient to ensure that the Chernoff bound is less than
unity and
The Chernoff bound can be tightened if X has a density function such
that
For where is the open interval over which is defined,
(1-87) implies that
Thus, we obtain the following version of the Chernoff bound:
where the minimum value is not required to be nonnegative. However, if
(1-94) holds, then the bound is less than 1/2, and
In soft-decision decoding, the encoded sequence or codeword with the largest
associated metric is converted into the decoded output. Let denote the
value of the metric associated with sequence of length L. Consider additive
metrics having the form
where is the symbol metric associated with symbol of the encoded se-
quence. Let label the correct sequence and label an incorrect one.
Let denote the probability that the metric for an incorrect codeword at
distance from the correct codeword exceeds the metric for the correct code-
word
.
By suitably relabeling the symbol metrics that may differ for the two
sequences, we obtain
where the inequality results because U(2) = U(1
)
does not necessarily cause
an error if it occurs. In all practical cases, (1-94) is satisfied for the random
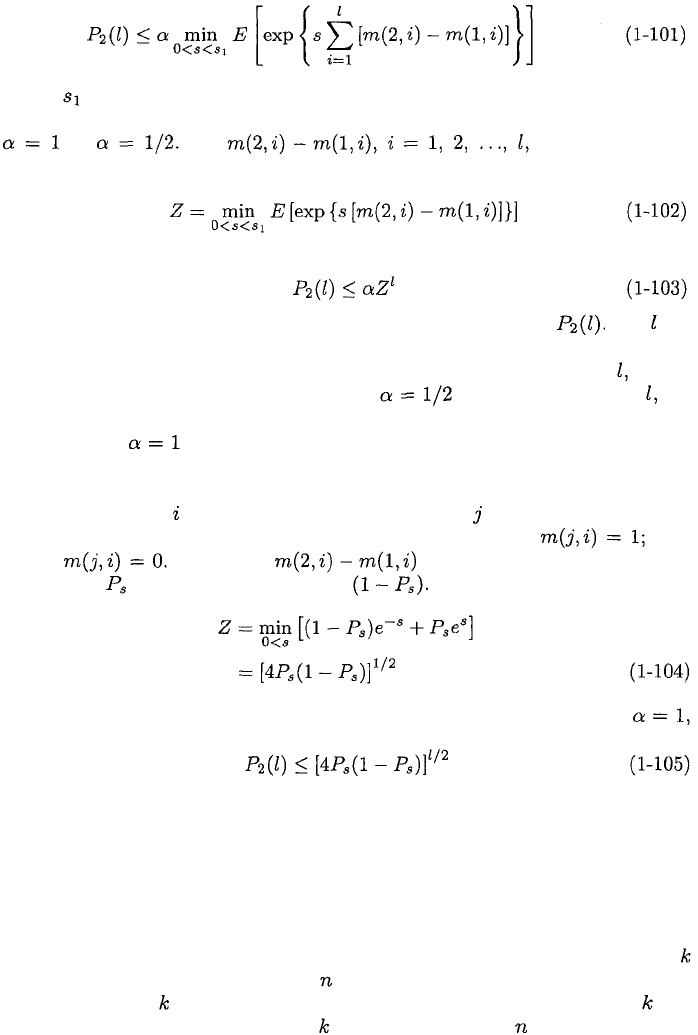
1.2.
CONVOLUTIONAL CODES AND TRELLIS CODES
27
variable X = U(2) – U
(1).
Therefore, the Chernoff bound implies that
where is the upper limit of the interval over which the expected value is
defined. Depending on which version of the Chernoff bound is valid, either
If are independent,
identically distributed random variables and we define
then
This bound is often much simpler to compute than the exact As in-
creases, the central-limit theorem implies that the distribution of X = U(2) –
U(1) approximates the Gaussian distribution. Thus, for large enough (1-95)
is satisfied when E[X] < 0, and we can set in (1-103). For small (1-
95) may be difficult to establish mathematically, but is often intuitively clear;
if not, setting in (1-103) is always valid.
These results can be applied to hard-decision decoding, which can be re-
garded as a special case of soft-decision decoding with the following symbol
metric. If symbol of a candidate binary sequence agrees with the corre-
sponding detected symbol at the demodulator output, then oth-
erwise Therefore, in (1-102) is equal to +1 with
probability and –1 with probability Thus,
for hard-decision decoding. Substituting this equation into (1-103) with
we obtain
This upper bound is not always tight but has great generality since no specific
assumptions have been made about the modulation or coding.
1.2
Convolutional Codes and Trellis Codes
In contrast to a block codeword, a convolutional codeword represents an entire
message of indefinite length. A convolutional encoder converts an input of
information bits into an output of code bits that are Boolean functions of
both the current input bits and the preceding information bits. After bits
are shifted into a shift register and bits are shifted out, code bits are read
out. Each code bit is a Boolean function of the outputs of selected shift-register
or
