Типовой расчёт по высшей математике
Подождите немного. Документ загружается.


Міністерство освіти та наук Украіни
Донецький Національний Технічний Універсітет
Автомобільно-дорожній інститут
Факультет АТР
Кафедра “Вища математика”
Типовий розрахунок
( варіант № 5 )
Виконав:
ст.гр.АТР-04 Шилкін В.А.
Перевірив:
док. Вовк Л.П.
Горлівка 2004

Задание №15
Даны координаты вершин пирамиды А
1
А
2
А
3
А
4
.
А
1
(10;6;6), А
2
(-2;8;2),A
3
(6;8;9), А
4
(7;10;3).
Найти:1)длину ребра А
1
А
2
;2)угол между рёбрами А
1
А
2
и А
1
А
4
; 3)угол между
ребром А
1
А
4
и гранью А
1
А
2
А
3
; 4)площадь грани А
1
А
2
А
3
;5)объем пирамиды;
6)уравнение прямой А
1
А
2
;7)уравнение плоскости А
1
А
2
А
3
;
8)уравнение высоты А
4
О.Сделать чертёж.
Выполнение работы
Для нахождения координат вектора используем правило: из координат
конца вычитаем координаты начала:
)4;2;12()62;68;102();;(
12121221
zzyyxxAA
;
)3;2;4()69;68;106();;(
13131331
zzyyxxAA
;
)3;4;3()63;610;107();;(
14141441
zzyyxxAA
;
1.Длина рёбер А
1
А
2
, А
1
А
3
, А
1
А
4
является абсолютной величиной их векторов
и находится по формуле:
222
zyx
, где x, y, z – координаты вектора.
164164144AA
21
;
299416AA
31
;
349169AA
41
;
2. Угол между рёбрами А
1
А
2
и А
1
А
4
равен углу между их направляющими
векторами.Найдём его по формуле:
5576
12836
34164
3)(4)(423)(12
AAAA
AAAA
)AA^Acos(A
4121
4121
4121
7499,0
5576
56
; Угол между рёбрами А
1
А
2
и А
1
А
4
равен
2441
3. Угол между прямой и плоскостью есть угол между направляющим вектором
прямой и нормальным вектором плоскости.
Вектор
перпендикулярен каждому из векторов
21
AA
и
31
AA
лежащих в
данной плоскости. Найдём нормальный вектор плоскости (А
1
А
2
А
3
) через
векторное произведение двух векторов:
k16j52i14836j8k24k16j6i
324
4212
kji
AAAAN
3121
i
;;;;;44
)16;52;14(
;
;Угол
между прямой и плоскостью можно найти по формуле:
,где А,B,С- координаты нормального вектора
плоскости;
l,m,n- координаты направляющего вектора прямой;
Значит,
;6533,0
107304
214
315634
4820842
)16(521434
)3()16(452)3(14
222
Sin
9740
;
222222
nmlCBA
CnBmAl
Sin
4. Площадь грани А
1
А
2
А
3
составляет половину абсолютная величины
векторного произведения векторов ,т.е.половину площади параллелограмма,
построенного на этих векторах.
.).(089,28
2
3156
3156
2
1
2
1
2
1
3121
321
едквNAAAAS
AAA
;
5. Объём пирамиды равен
6
1
части объёма параллелепипеда, построенного на
векторах
21
AA
,
31
AA
и
41
AA
. Объём параллелепипеда численно равен
смешанному произведению этих векторов:
(
21
AA
,
31
AA
,
41
AA
)=
343
324
4212
2142414424186472
;
.).(7,35
6
214
4321
едкубV
AAAA
6. Каноническое уравнение прямой выглядит :
;
12
1
12
1
12
1
zz
zz
yy
yy
xx
xx
Найдём каноническое уравнение прямой
21
AA
:
;
4
6
2
6
12
10
zyx
7. 7.1Уравнение плоскости
),,(
321
AAA
представим через уравнение плоскости,
которая проходит через три точки:
0
131313
121212
111
zzyyxx
zzyyxx
zzyyxx
;- уравнение плоскости, которая проходит через три
точки; А
1
(10;6;6), А
2
(-2;8;2),A
3
(6;8;9) - три точки плоскости;
0
324
4212
6610
zyx
;
Приведём подобные в левой части уравнения:
24
212
)6(
34
412
)6(
32
42
)10( zyx
)6(16)6(52)10(14 zyx
=
96163125214014 zyx
356165214 zyx
;
0356165214 zyx
;- уравнение плоскости А
1
А
2
А
3
;
7.2 Зная нормальный вектор плоскости
)16;52;14(
и координату точки
принадлежащей этой плоскости (причём этой точкой может быть как т. А
1
(10;6;6),так
А
2
(-2;8;2)илиA
3
(6;8;9)- все они
пл.
),,(
321
AAA
)через общее уравнение
плоскости :
0 DCzByAx
, где A,B,C- координаты нормального вектора плоскости;
x,y,z- координаты вектора A
1
;
06166521014 D
;35696312140 D
Уравнение плоскости А
1
А
2
А
3
будет выглядеть:
0356165214 zyx
8. Найдём уравнение высоты А
4
О.Направляющий вектор высоты А
4
О совпадает
с нормальным вектором плоскости А
1
А
2
А
3
, поэтому их координаты равны.
Итак, каноническое уравнение высоты примет вид:
p
zz
n
yy
m
xx
444
;
S
;
16;52;14
;
16
3
52
10
14
7
zyx
;
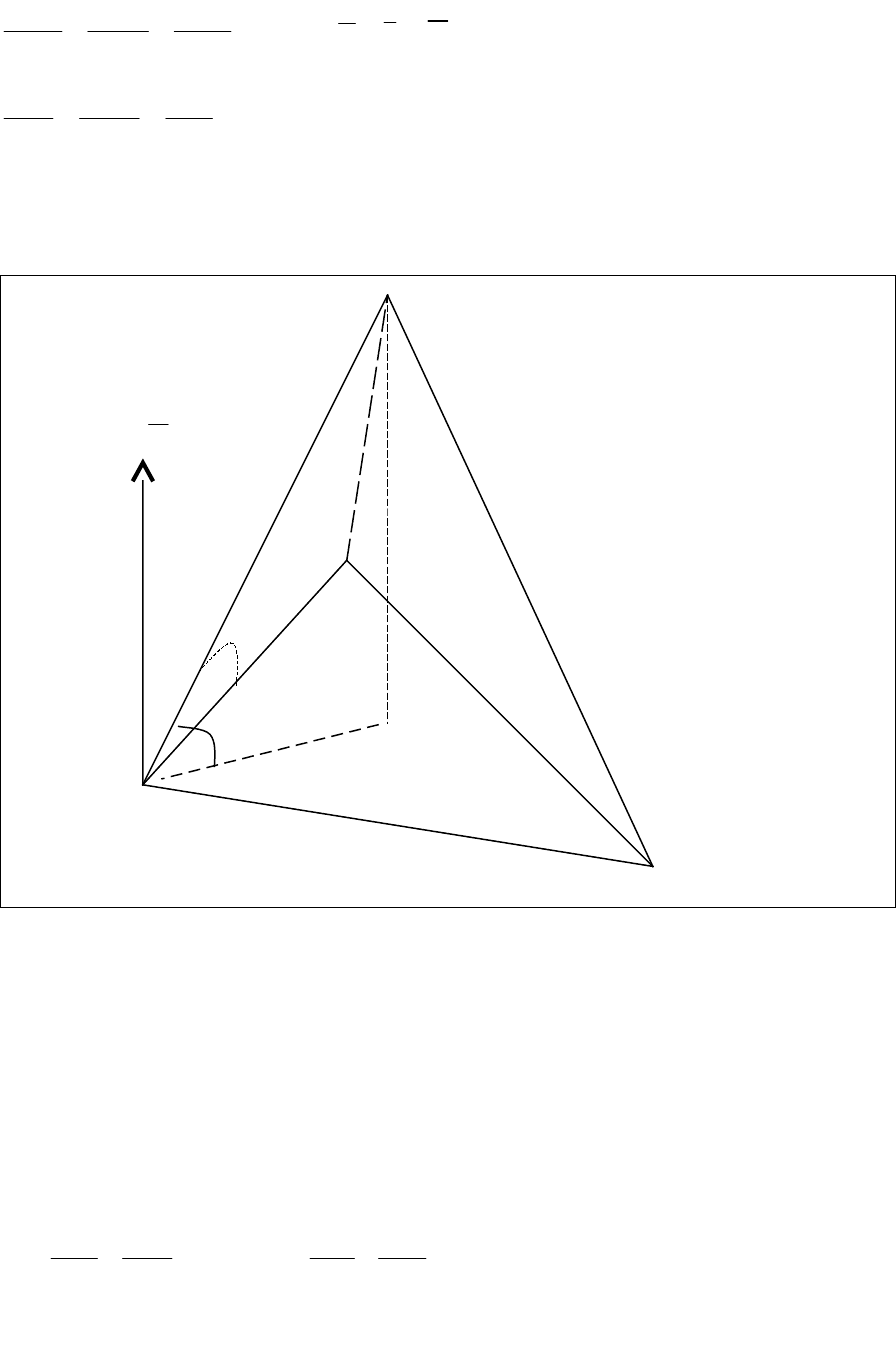
Чертёж пирамиды.
SHAPE \* MERGEFORMAT
Задание № 25
Даны вершины А (-3;-2),В(4;-1),С(1;3) трапеции АBCD (
BCAD //
). Известно,
что диагонали трапеции взаимно перпендикулярны (
21
). Найти координаты
вершины D этой трапеции. Сделать чертёж.
Решение
Cоставим уравнение прямой АС проходящей через две точки А (-3;-2) и В (4;-1)
;
23
2
31
3
:
yx
AC
5
2
4
3
:
yx
AC
;
84155 yx
;
0745 yx
;
2
1
3
4
4
7
4
5
xy
;
4
5
AC
k
; - угловой коэффициент АС;
Известно, что угловые коэффициенты двух перпендикулярных прямых
являются обратными и противоположными величинами, тогда если по условию
диагонали трапеции взаимно перпендикулярны, то:
AC
BD
k
k
1
;
5
4
BD
k
;
Точка В(4;-1)
ВD.Составим уравнение ВD:
bxyBD
5
4
:
;
5
11
5
516
5
16
1
b
;
5
11
5
4
xy
;
01154 yx
;
Сторона BC параллельна AD, значит, угловые коэффициенты этих прямых
равны. Составим уравнение ВС:
;
13
1
41
4
:
yx
BC
33164: yxBC
;
01334: yxBC
;
;
3
13
3
4
: xyBC
3
4
ADBC
kk
;
А (-3;-2)
AD:
1
3
3
4
2 b
6
1
b
Итак, уравнение прямой AD:
;6
3
4
xy
1843 xy
;
01834 yx
;
Т. к.,
AD
пересекается с
BD
в точке
D
, то координаты этой точки найдём,
решив систему уравнений:
-
0;1834
0,1154
yx
yx
09220 y
;
2
29
y
;
Подставляем значение у, в первое уравнение системы:
011
2
295
4
x
;
0221458 x
;
1238 x
;
8
123
x
;
Итак, вершина D трапеции АВСD имеет координаты:
)
2
29
;
8
123
(D
;
Ответ:
)
2
29
;
8
123
(D
;
Задание 55
Дана система линейных уравнений. Доказать её совместимость и решить
двумя способами: а) метод Гаусса;
б) средствами матричного исчисления.
Выполнение задания
а) метод Гаусcа
11;4х2х3х
11,2х4х3х
4,хх2х
321
321
321
Решение систем линейных уравнений методом Гаусса (метод
последовательного исключения неизвестных ) основывается на элементарных
превращениях системы уравнений в эквивалентную сходную систему, при
разрешении которой не возникает трудностей. Особенность только в том, что к
сходному виду приводят не саму систему, а ее расширенную матрицу (матрицу
со столбцом свободных членов):
~
0
10
7
660
1110
151
~
0
10
7
660
1110
151
~
0
11
7
660
243
151
~
11
11
4
423
243
112
D
233
: CCС
122
3: CCС
322
2: CCС
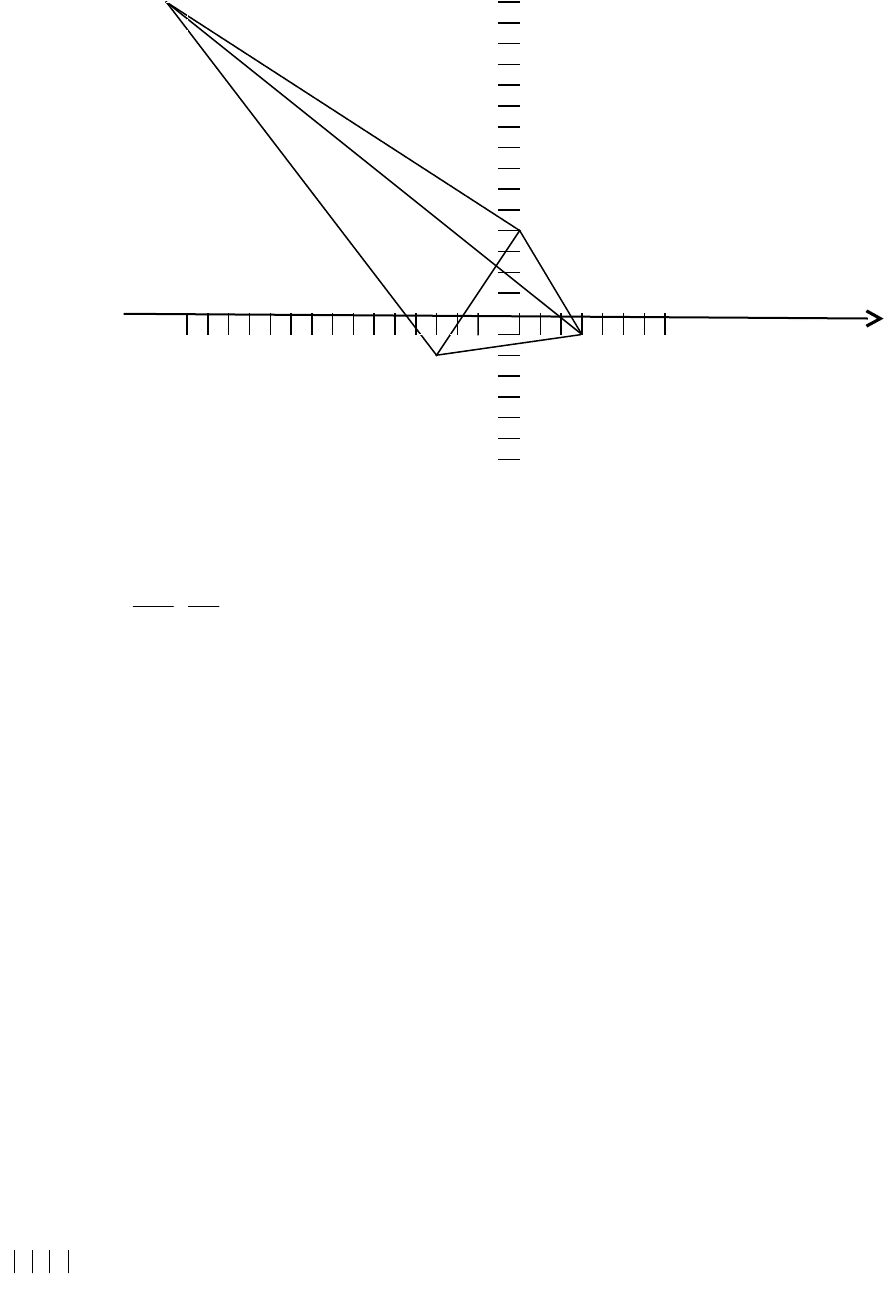
C (1;3)
B (4;-1)A (-3;-2)
У
Х
D(-15,375;14,5)
2
0
3
1
2
15
2
3
2
4
3
14

211
: CCС
~
60
10
7
6000
1110
151
;
Матрица переведена к треугольному виду.
3)()( nArDr
;
Теорема Кронеккера-Капелли гласит:
Если система линейных уравнений содержит n неизвестных и:
1)
nArDr )()(
, то система совместима и имеет единственное решение;
2)
nArDr )()(
, то система совместима и имеет множество решений;
3)
)()( ArDr
, то система не совместима, т.е. не имеет решений;
Составим систему уравнений, из которой найдём неизвестные:
6060х
-1011х- х
7х5хх-
3
3
321
-
;1
,1
,3
3
2
1
x
x
x
Итак, методом Гаусcа получаем x
1
=3, x
2
=1, x
3
=1 ;
б) Решим уравнение способом обратной матрицы.
AA
423
243
112
;
11
11
4
B
;
BAX
1
;
602126623
423
243
112
;
0
Матрица А не выраждена и квадратна - это удовлетворяет условию
существования обратной матрицы. Составим матрицу
1
A
обратную матрице А:
332313
322212
312111
AAA
AAA
AAА
1
A
;
Вычислим алгебраическое дополнение для матрицы А
-1
:
12416
11
A
;
6
21
A
;
6
31
A
;
18)612(
12
A
;
11
22
A
;
1
32
A
;
18126
13
A
;
1
23
A
;
11
33
A
;
;
11 1 18-
1 11 18-
6 6 12
60
1
1
A
3
2
1
1
1
3
60
60
180
60
1
1211172-
1112172-
666648
60
1
11
11
4
11 1 18-
1 11 18-
6 6 12
60
1
x
x
x
Х
;
Итак, убеждаемся, что корни данной системы уравнения
;3
1
x
;1
2
x
1
3
x
;
Ответ:
;3
1
x
;1
2
x
1
3
x
;
11423
11243
42
321
321
321
ххх
ххх
ххх
Задание № 35
Составить уравнение и построить линию, расстояние каждой точки которой
равноудалена от точки А(2;0) и от прямой 2х+5=0 относятся, как 4:5.
Решение.
Предположим точка М (x; у) принадлежит данной кривой.Расстояние от точки
М до т.А можно определить определяется как модуль вектора:
22
)1()3( yxMA
;
Расстояние от точки до прямой определяется по формуле:
2
52
4
52
22
xx
BA
CBA
d
yx
; - расстояние от точки М до прямой 2х+5=0;
Согласно условию:
5
4
d
MA
;
5
4
52
)2(2
22
x
yx
;
524)2(10
22
xyx
;
)25204(16)44(100
222
xxyxx
;
040040010064400320100
222
yxxxx
;
010072036
22
yxx
;
Преобразуем данное уравнение:
0100)20(36
22
yxx
;
01003600)10010`2(36
22
yxx
;
3600100)10(36
22
yx
;
1
36100
)10(
yx
;- это уравнение эллипса со смещённым центром О(10;0);
а=10; в=6;
86436100
22
вac
; - фокальная полуось;
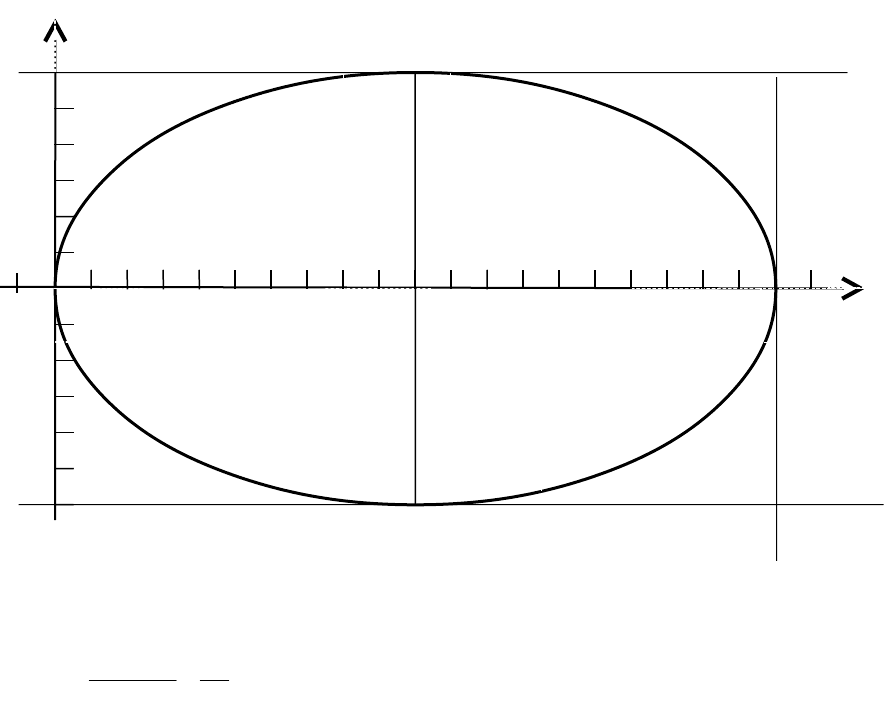
Ответ:
1
36100
)10(
22
yx
;
- a(0;0)
у
х
(2;0)
с(10;0)
в(0;6)
(18;0) а(20;0)
- в(0;-6)
6
6
2 20
0
Задание № 115
Найти пределы функции.
а)
15
562
lim
2
2
xx
xx
x
;
Чтобы разрешить неопределённость вида
, нужно разделить числитель и
знаменатель на высшую степень аргумента, что не изменит величины предела.
5
2
005
002
lim
11
5
56
2
lim
15
562
lim
2
2
2
2
xxx
x
x
x
x
xx
xx
;
б)
0
011
lim
2
2
0
x
x
x
;
Чтобы избавиться от неопределённости вида
0
0
выражение стоящее под
знаком предела домножим на сопряженное выражение.
22
2
0
22
22
0
2
2
0
11
)1(1
lim
11
1111
lim
0
011
lim
xx
x
xx
xx
x
x
xxx
2
1
011
1
lim
1
1
lim
0
2
0
xx
x
;
в) Используем формулу первого замечательного:
2
2
0
2
2
0
2
3
0
sincos
lim
cos1cos
lim
0
0coscos
lim
x
xx
x
xx
x
xx
xxx
111coslim
sin
lim
0
2
0
2
x
x
x
xx
;
г)Вынесем знак логарифма за знак предела функции:
1
ln
1
1limln
1
lnlimln1lnlim
e
x
xx
x
xxxx
xxx
;
Ответ: а)
5
2
; б)
2
1
;в) 1; г) 1;
Задание № 145
Найти производные функций: a)
22
xa
x
y
; б)
x
x
y
2
2
cos32
sin
; в)
1
ln
x
xx
y
;
г)
x
arctgxy
ln
)(
; д)
01)1)(1(
yx
ee
;
Выполнение задания
a)
22
xa
x
y
;
Производная частного находится по формуле:
2
)()(
v
uvvu
v
u
y
;
