Типовой расчёт по высшей математике
Подождите немного. Документ загружается.

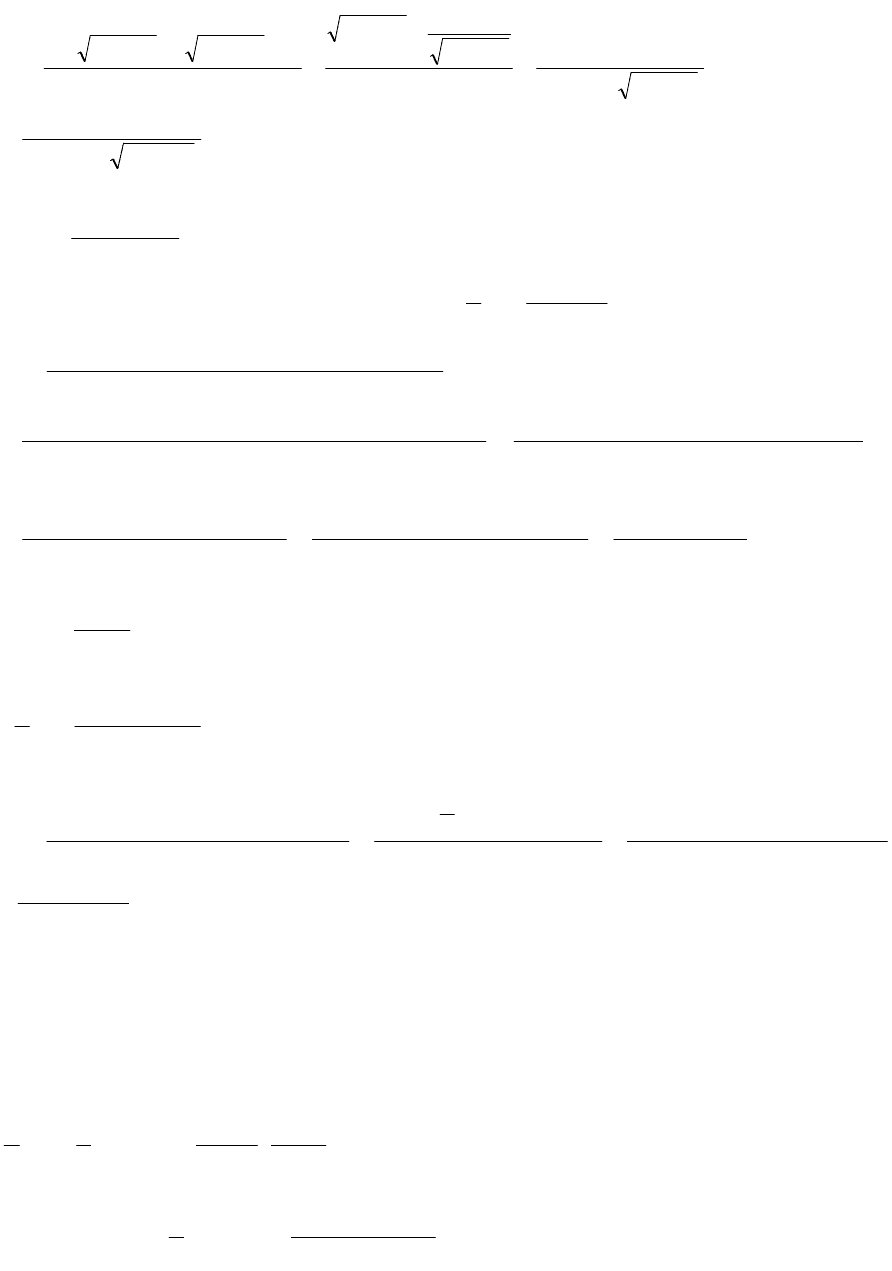
2222
222
22
22
2
22
22
2222
)()(
xaxa
xxa
xa
xa
x
xa
xa
xxaxax
y
2222
2
xaxa
a
б)
x
x
y
2
2
cos32
sin
;
Используем предыдущую формулу:
2
v
uvvu
v
u
;
22
2222
)cos32(
sin)cos32()cos32(sin
x
xxxx
y
22
22
)cos32(
sinsincos6)cos32()cossin2(
x
xxxxxx
22
22
)cos32(
sin2sin3)cos32(2sin
x
xxxx
2222
22
22
22
)cos32(
2sin5
)cos32(
))sin(cos32(2sin
)cos32(
)sin3cos32(2sin
x
x
x
xxx
x
xxx
;
в)
1
ln
x
xx
y
;
В данном случае используем такие формулы :
2
)()(
v
uvvu
v
u
;
uvvuvu
)(
;
222
)1(
ln1lnln
)1(
ln)1)((ln
)1(
ln)1()1()ln(
x
xxxxxx
x
xxx
x
x
x
x
xxxxxx
y
=
=
2
)1(
1ln
x
xx
;
г)
x
arctgxy
ln
)(
;
Прологарифмируем обе части функции по основе е.
arctgxxy lnlnln
2
1
1ln
ln
11
x
arctgx
x
arctgx
x
y
y
;
Выразим производную:
)
)1(
ln
ln
1
()(
2
ln
arctgxx
x
arctgx
x
arctgxy
x
;
д)
01)1)(1(
yx
ee
;
Такая функция называется неявной.

Изменяемой называется функция, которая неявно зависит от х, если это
изменяемая связана зависимостью F(x;y)=0, y которой не х, не у нельзя
определить в явном виде.
0)1()1()1()1(
xyyx
eyeee
;
0)1()1(
xyyx
eyeee
;
)1(
)1(
xy
yx
ee
ee
y
;
Ответ: а)
2222
2
xaxa
a
; б)
22
)cos32(
2sin5
x
x
;в)
2
)1(
1ln
x
xx
; д)
)1(
)1(
xy
yx
ee
ee
y
;
г)
)
)1(
ln
ln
1
()(
2
ln
arctgxx
x
arctgx
x
arctgxy
x
;
Задание № 155
Найти
dx
dy
и
2
2
dx
yd
для заданных функций:
а)
arctgxy
;
Найдём первую производную:
2
1
1
)(
x
arctgxy
;
Определим вторую производную:
222222
22
)1(
2
)1(
)20(10
)1(
)1()1(
x
x
x
x
x
xx
y
;
Ответ:
22
)1(
2
x
x
y
;
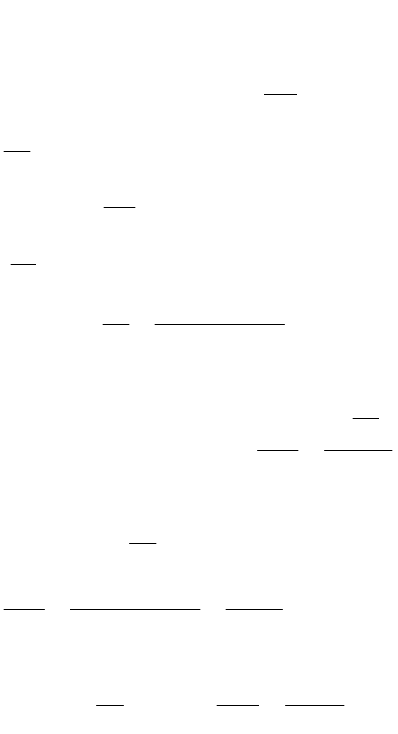
б)
;sin2
,cos3
3
2
ty
tx
Данная функция задана параметрично. Решим её пошагово:
Первый шаг. Найдём
dt
dx
:
ttt
dt
dx
2sin3)sin(cos23
;
Найдём
dt
dy
:
tt
dt
dy
cossin32
2
;
Найдём
t
tt
tt
dx
dy
sin
sincos6
cossin6
2
;
Второй шаг. Найдём
dx
dx
dy
d
dx
yd
2
2
:
Найдём
t
dx
dy
d cos
;
ttt
t
dx
yd
sin6
1
cossin6
cos
2
2
;
Ответ:
tdx
yd
t
dx
dy
sin6
1
;sin
2
2
;
Задание № 185
Найдём радиус основания и высоты конуса наименьшего объёма , описанного
около шара радиуса R.
Выполнение задания
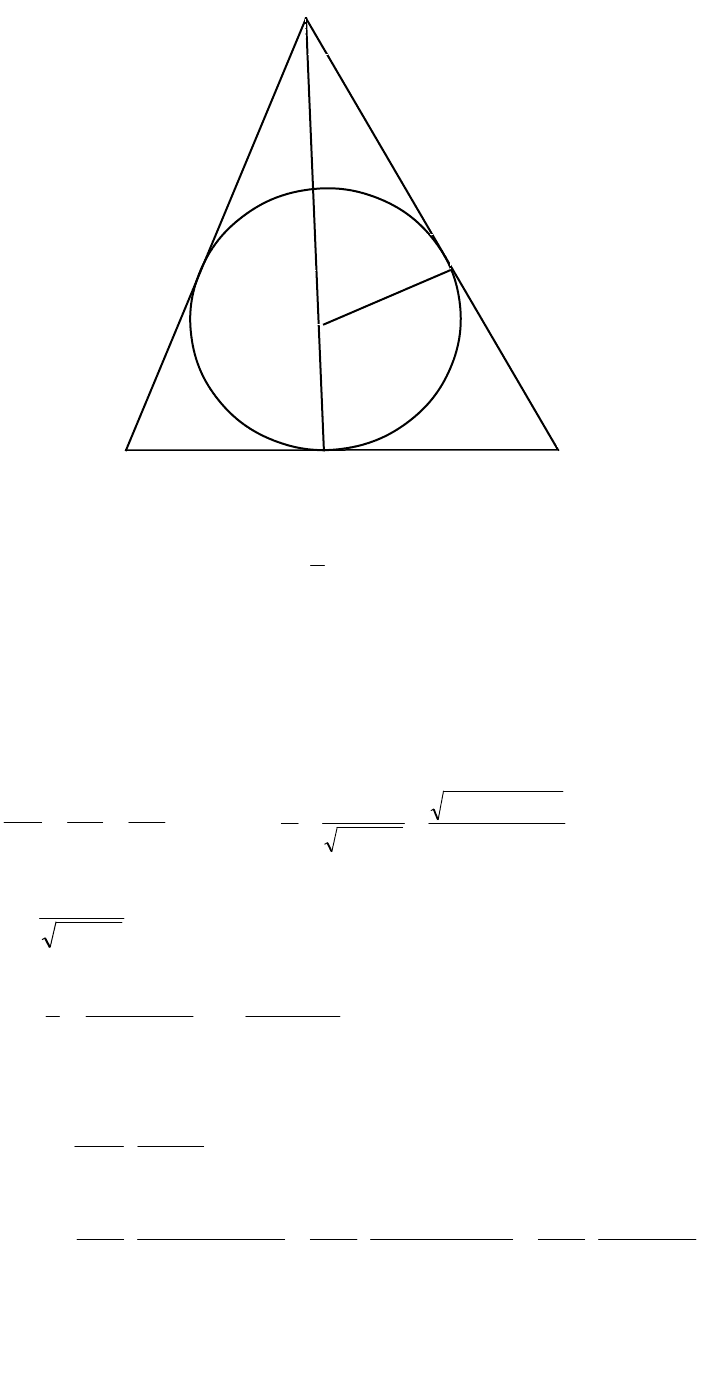
Объём конуса равен :
HrV
2
3
1
;
Осевое сечение конуса представляет собой равнобедренный треугольник.
В задаче задан радиус окружности R. Обозначим радиус основания конуса
KС=АK=r, высоту ВС=h.
Из подобия треугольников
ВCK
и
ВNO
запишем соотношение сторон:
BK
BN
BC
OB
KC
ON
или
h
RRh
rh
Rh
r
R
22
22
)(
;
Rhh
Rh
r
2
2
;
)2(3
)2(
3
1
22
2
22
Rh
hR
h
Rhh
hR
V
Находим производную V (h),чтобы впоследствии найти наименьшую величину
объёма:
Rh
hR
hV
23
)(
22
;
2
22
2
222
2
22
)2(
42
3
)2(
42
3
)2(
)2(2
3
)(
Rh
RhhR
Rh
hRhhR
Rh
hRhhR
hV
;
Находим точку экстремума:
0
V
;
А
K
N
O
В
С
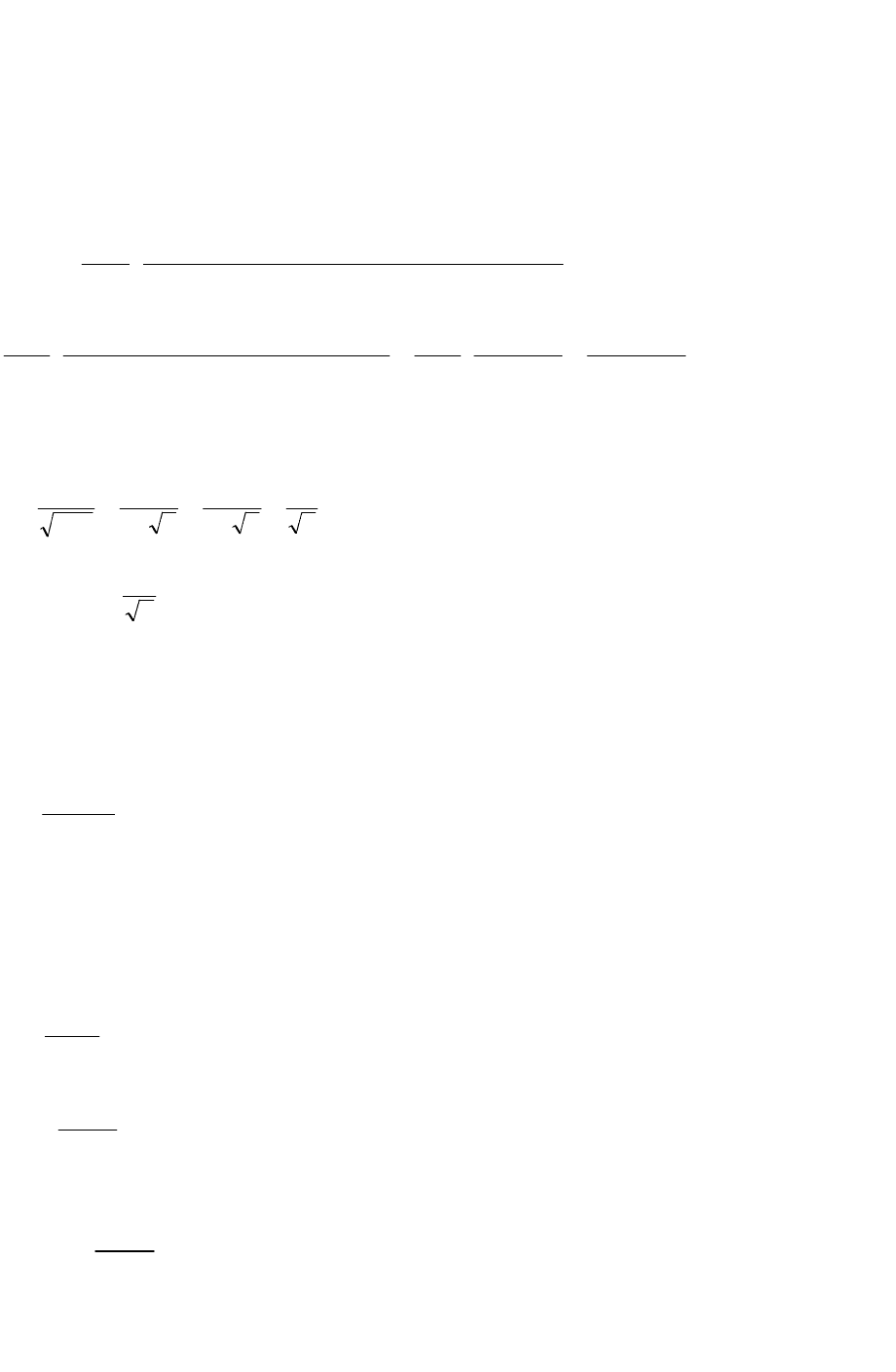
04
2
Rhh
;
0h
;
Rh 4
;
Т.к.
hR2
то
0h
- не входит в рассматриваемый интервал. Исследуем
значение
Rh 2
. Находим вторую производную:
3
222
)2(
)2(2)4()2)(42(
3
)(
Rh
RhRhhRhRhR
hV
3
4
3
22
3
2222
)2(3
8
)2(
8
3
)2(
828442
3
Rh
R
Rh
RR
Rh
RhhRRhRhhR
;
значение
0
V
при
Rh 4
функция примет минимум.
Итак, r равен:
2
2
22
4
22
4
8
4
22
2
2
R
R
R
R
R
R
R
r
;
Ответ:
Rh
R
r 4;
2
2
;
Задание № 195
Исследовать методом дифференциального исчисления функцию
)(xty
и
используя результаты исследования, построить ёё график.
)1(
2
3
x
x
y
Решение
Находим область определения данной функции
)( уD
:
)( уD
:
);( x
;
Данная функция существует во всём интервале области определения. Точек
разрыва нет. Проверим поведение графика функции на подходе к
и
1
2
3
lim
x
x
x
;
1
lim
2
3
x
x
x
;
Вертикальных асимптот нет. Определяем, является ли данная функция чётной
или нечётной.
)(
1
)(
2
xy
x
x
xy
Функция нечётная её график симметричен относительно начала координат.
Определим уравнение наклонных асимптот. Ур-е наклонных асимптот имеет
вид:
bkxy
В нашем случае, получаем:
1
1
lim
1
1
lim
2
2
2
3
x
x
x
x
x
k
xx
0
1
lim
1
lim
1
lim
22
33
2
3
x
x
x
xxx
x
x
x
b
xxx
Итак, уравнение наклонных асимптот имеет вид
xy
Найдём промежутки монотонности и точки экстремума функции. Для этого
найдём
y
:
22
24
22
424
22
322
)1(
3
)1(
233
)1(
2)1(3
x
xx
x
xxx
x
xxxx
y
Найдём точки экстремума и промежутки монотонности :
0)3(
22
xx
0x
03
2
x
01
2
x
Проверим, является ли данная точка критической:
Точка
0x
не является критической точкой. Промежутков монотонности нет.
Найдём интервалы выпуклости и вогнутости. Для этого найдём
y
:
42
242223
)1(
)3(2)1(2)1)(64(
x
xxxxxxx
y
32
3
32
35325
)1(
26
)1(
)1246644
x
xx
x
xxxxxx
0
y
026
3
xx
01
2
x
0x
026
3
x
62
3
x
3
2
x
3x
3
4
3
)3( y
0)0( y
3
4
3
)3( y
+
+
0
х
0
+
+ --
3
3
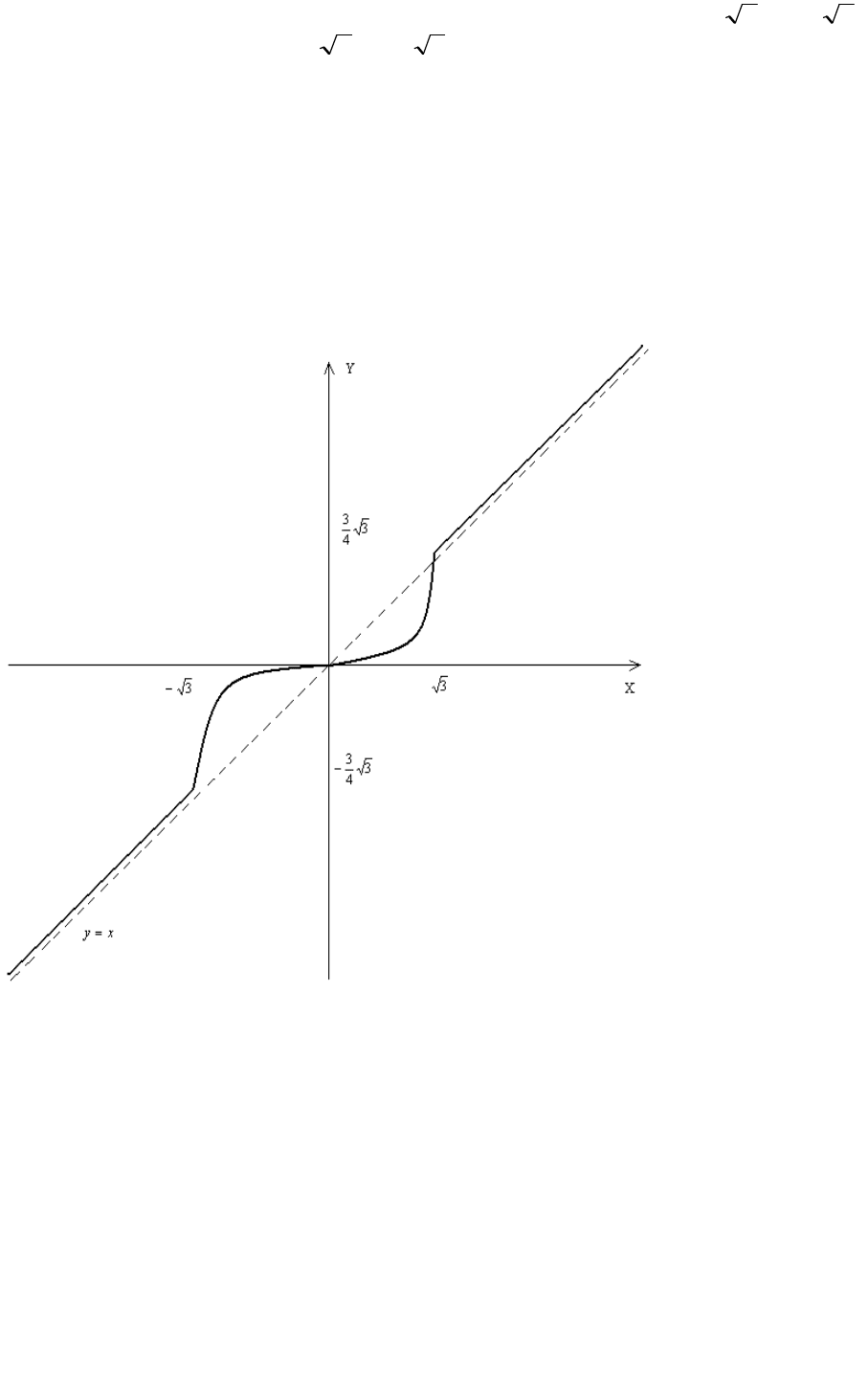
График данной функции выпуклый вверх на интервалах
)3;(
;
)3;0(
; и
выгнутый на интервалах
)0;3(
;
);3(
. Находим точки пересечения с осями
координат:
Ось ох:
0y
0x
Ось оу:
0x
0y
Теперь мы имеем возможности построить график функции, т.к. все
необходимые вычисления произвели, строим:
Задание № 205
)4ln(
2
xy
1)Найдём область определения функции
04
2
x
0)2)(2( xx
);2()2;( xє
2)х= -2, х= 2 ;
)4ln(lim
2
0
x
iz
;

)4ln(lim
2
0
x
iz
;
Исследуем функцию на существование вертикальных асимптот. Если функция
имеет в некоторой точке
0
x
разрыв 2-го порядка, то
0
xx
уравнение
вертикальной асимптоты
2x
и
2x
вертикальные асимптоты графика
функции.
3) Установить чётность или не чётность функции.
Функция называется чётной если она удовлетворяет уравнению
)()( xfxf
( график симметричен относительно начала координат).
Функция называется не чётной, если она удовлетворяет уравнению
)()( xfxf
, и её график симметричен относительно оси координат.
)4ln()4)ln(()(
22
xxxf
Функция чётная и её график симметричен
относительно оси координат.
4) Найдём наклонные и горизонтальные асимптоты:
bkxy
x
x
x
y
k
))4(ln(
limlim
2
;
04
2
lim
2
x
x
)4(ln(lim)(lim
2
xKxy
xx
;- наклонные асимптоты отсутствуют.
5) Найдём интервалы монотонности функции и её экстремумы.
Интервал монотонности это интервал, в которой функция не меняет знак.
Экстремум это точка в которой функция меняет знак.
;
4
2
))'4(ln("
2
2
x
x
xy
0
y
0
4
2
2
x
x
;
0x
но точка 0 не входит в область определения функции, экстремумов нет.
Функция возрастает на всём интервале.
);2()2;(
6) Найдём перегибы функции
22
2
22
22
22
2
2
)4(
)82(
)4(
482
)4(
)2(2)4(2
4
2
"
x
x
x
xx
x
xxx
x
x
y
;
0"y
Перегибов графика нет.
7) График функции.
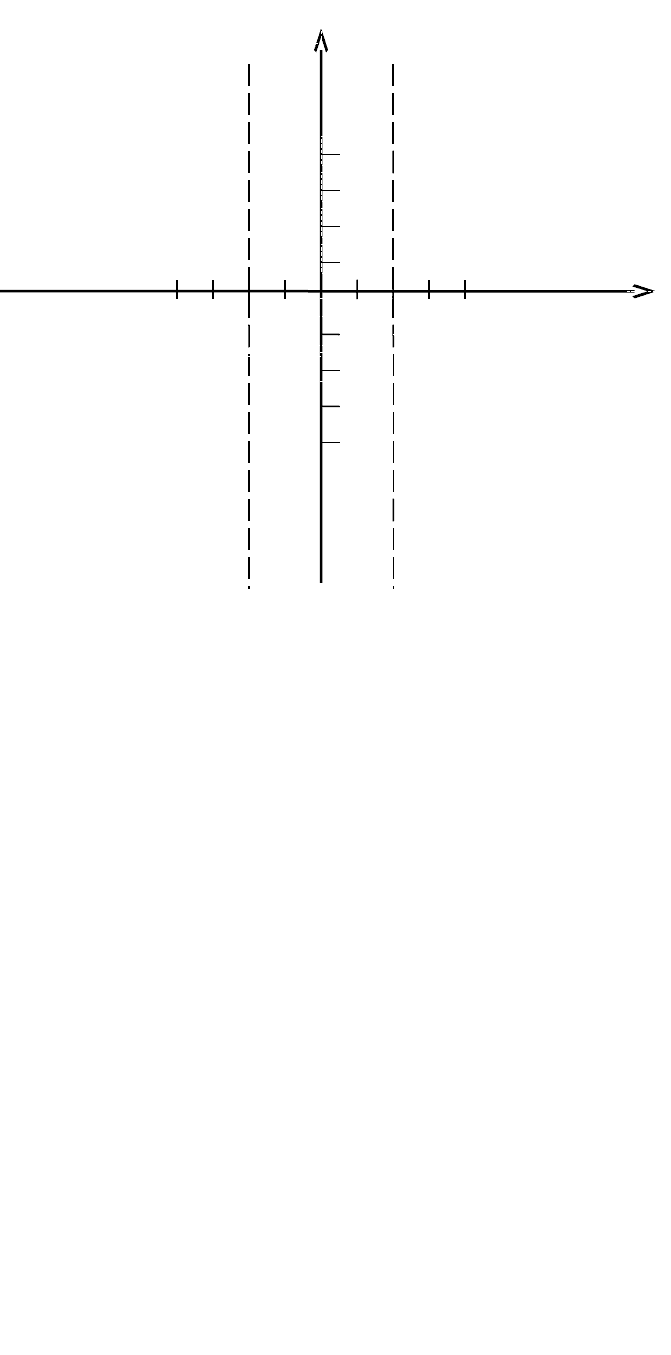
Задание № 135
2,1
20,
0,
2
)(
xx
xx
xx
xf
Рассмотрим т. х=0 . Находим односторонние пределы в этой точке.
У
Х
-4 -3 -2 -1 1 2 3 4
1
2
3
4
-1
-2
-3
-4
)0(0)(lim)(lim
0000
fxxf
xx
0lim)(lim
2
0000
xxf
xx
В точке х=0 функция
)(xf
непрерывна
Исследуем точку х=2
;4lim)(lim
2
0202
xxf
xx
;3)1(lim)(lim
0202
xxf
xx
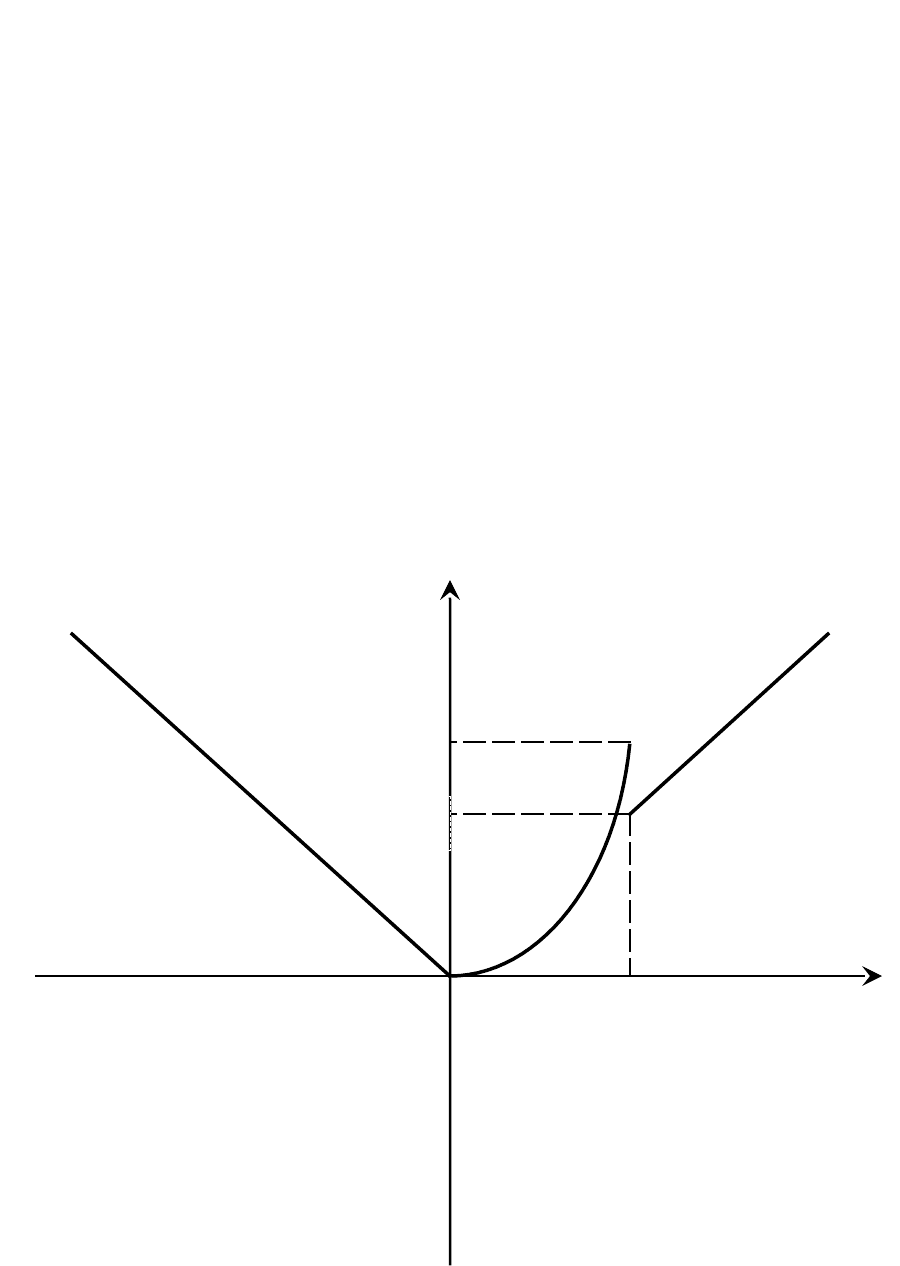
Таким образом в точке х=2 функция
)(xf
терпит разрыв 1-го рода.
1xy
xy
У
Х
4
3
2
xy
2
