Термодинамика, проверочные работы по Василевскому
Подождите немного. Документ загружается.

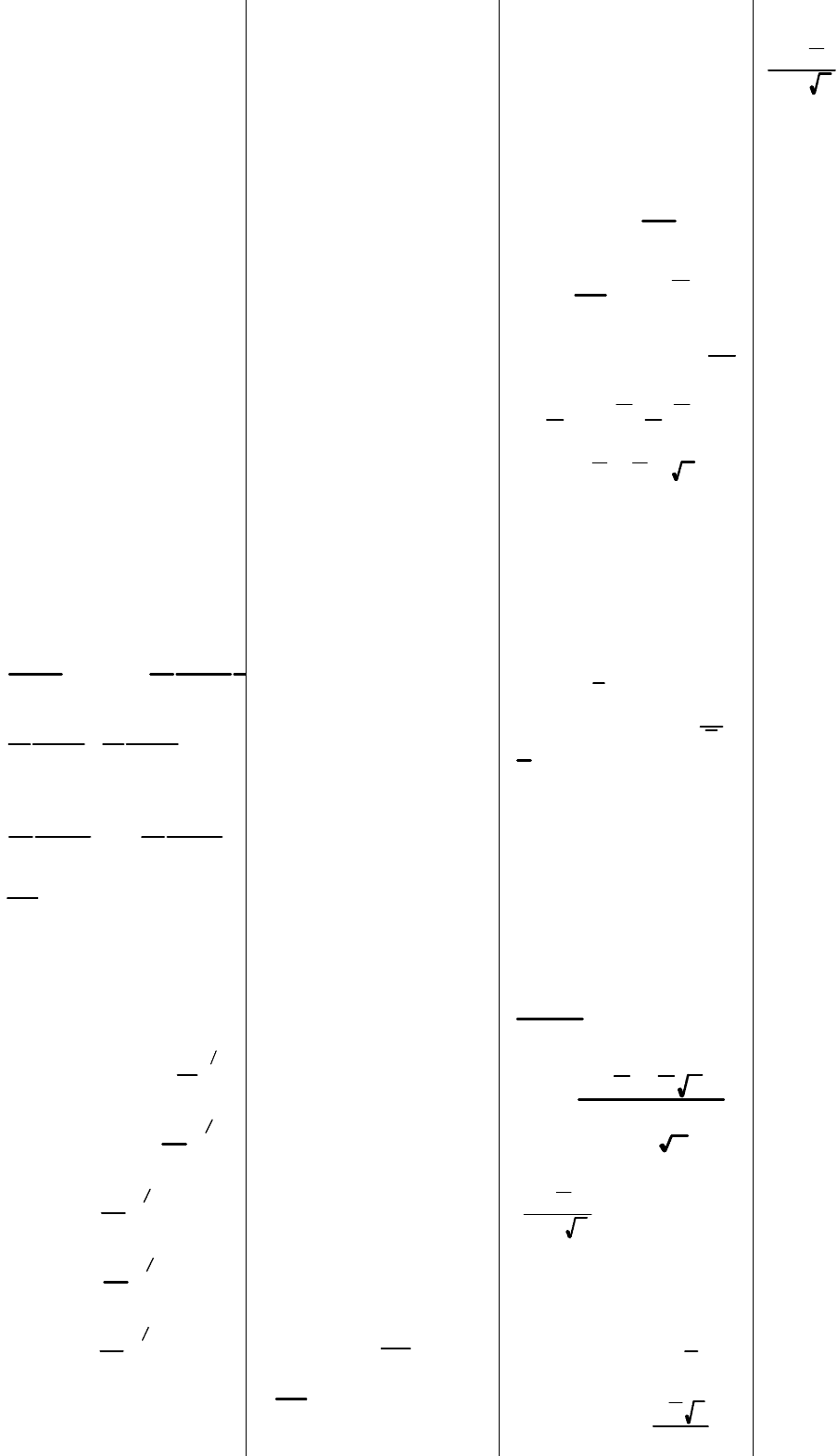
1.Идеальный газ в МКТ. Вывод распределения
Максвелла. Модель ИГ 1) у нас ч-ы одного сорта; 2)
каждую час-у хар-м только одним параметром - m. Ч-ы
представляются либо мат точками, либо маленькими абс
твердыми непроницаемыми шариками. Б пользоваться
классической механикой и для описания состояния 1 ч-ы б
исп-ть тройку координат и соотв-но 3 проекции скорости;
3) физические условия в которых находится час-а: газ
имеет только 1 внеш параметр- объем. Разговор идет о
равновесной т\д системе (концентрация ч-ц везде
одинакова, везде одно и тоже давление тем-ры; 4) взаим-и
ч-ц на расстоянии нет. Обмен энергией и импульсом м-у ч-
ми происходит путем упругих столкновений. Возм-ть не
включать столкновения в расчет связ-на с тем, что в кажд
момент времени столкновение претерпевает очень
небольшое кол-во ч-ц, в ост время она не испыт
соударений. Основным понятием стат. физики явл.
распред. вероятн. для различных сост-ий отдельных ч-ц
или всей с-мы в целом. Воспользуемся Максвелловской
теорией ид-го газа. Поставим целью найти распределение
вероятности для скоростей ч-ц. Предположим, что все
направления дв-ия мол-лы в пространстве являются
равновероятными. Это вытекает из представлений о
полной неупорядоченности дв-ия ч-ц в равнов-ом
состоянии газа. Допустим также, что все 3 проекции
скорости v
x
, v
y
, v
z
представляют собой незав-ые др. от др.
случай ные величины. Запишем распределение вер-ти для
v
x
, v
y
, v
z
:
,)
2
()(
x
dv
x
vf
x
vdW
,)
2
()(
y
dv
y
vf
y
vdW
z
dvvf
x
vdW )
2
()(
. 1)плотность
вероятности для всех проекций выражается одной и той же
ф-ей f в силу их полного равноправия. 2) распред.
вероятности может зависеть лишь от модуля проекции, но
не от ее знака. Поэтому аргументом ф-ции f во всех 3 фор-
ах служит квадрат проекции. Вероятность того, что мол-ла
будет двигатся с некоторой скоростью
v
, равна вер-
сти того, что 3 проек. скорости примут соответствующие
значения v
x
, v
y
, v
z
.
).,,()(
z
v
y
v
x
vdWvdW
запишем распределение в виде
.
),,()(
z
dv
y
dv
x
dv
z
v
y
v
x
vFvdW
(**).Вследствие равновер. всех направлений движ. F может
зависеть непосредственно тоько от v
2
=v
2
x
+v
2
y
+v
2
z
, но не от
v
x
, v
y
, v
z
в отдельности. Т.к. v
x
, v
y
, v
z
независимые
случайные величины, по теореме умножения вероятностей
dW(v
x
,v
y
,v
z
)=dW(v
x
)dW(v
y
)dW(v
z
) и, следовательно,
F(v2)=f(v
2
x
)f(v
2
y
)f(v
2
z
) (*). Чтобы найти вид ф-ции F и f
прологорифмируем это равенство lnF(v
2
)=lnf(v
2
x
)+lnf(v
2
y
)
+lnf(v
2
z
), продиф. по v
2
x
:
)
2
(
1
)
2
(
)
2
(
)
2
(
1
)
2
(ln
)
2
( vd
dF
F
x
v
v
vd
dF
F
vF
x
v
проекции скорости незав. переменные, поэтому получаем
.
)
2
(
1
)
2
(
1
x
vd
df
f
vd
dF
F
равенство
2 ф-ций различных независимых переменных имеет место
тогда и только тогда , когда они равны одной и той же
постоянной. Полагая
.
)
2
(
1
,
)
2
(
1
x
vd
df
f
vd
dF
F
2
v
F
dF
интегрируем
BF ln
2
ln
из решения
находим F(v)=Bexp(-v
2
); f(v
x
)=Aexp(-v
2
x
). Очевидно, что
>0, иначе, чем больше скорость, тем больше была бы ее
вер-сть. A, B из условия нормировки, из(*) следует, что
B=A
3
.
1)
2
exp(
x
dv
x
vA
по
табличной формуле находим
21
A
распределение для скоростей (**) примет вид
z
dv
y
dv
x
dvv
z
v
y
v
x
vdW )
2
exp(
23
),,(
, для проекций
x
dv
x
v
x
vdW )
2
exp(
23
)(
,
y
dv
y
v
y
vdW )
2
exp(
23
)(
,
z
dv
z
v
z
vdW )
2
exp(
23
)(
, определяет число молекул с различными скоростями.
Это специфич. характ. с-мы.
3. Квазинезависимые подсистемы. 2 подсистемы счит-ся
квази-е, если вып-ся соот-ие: Энергия всей системы равна
сумме энергий подсистем с достаточной степенью
точности. Е=Е
1
+Е
2
+Е
св
мы пренебрегаем слагаемым Е
св
. для
квазинезавис систем хар-но 1) аспект всевозможных
состояний 1 подсист, считая ее чуть ли не изолир от др
подсист. 2) то в каком состоянии нах-ся 1 подсист никак не
зависит от того в каком состоянии нах-ся подсист. 3) число
возможных состояний системы нах-ся как произведение
числа возможных состояний подсистемы.
(Е)=
1
(Е
1
)(Е
2
), Е
1
+Е
2
=Е (Е
1
Е
2
-фиксированы). Если
системы обмениваются энергией, оставаясь квазинезавис,
то н найти сумму
)
2
(
2
0
2
)
2
(
1
)( Е
Е
Е
ЕЕЕ
Модель системы. Микpоскоп. сост. системы.
N>>1 N
A
10
23
Ч-ы непосредственно не наблюдаемы
1) какие ч-ы и в каком кол-ве входят в нашу систему; 2)
физические условия в которых находится ч-а. Описание
физических условий делается с помощью величин -
внешних параметров (наиболее популярен V) 3) закон
взаимод-й ч-ц. Наиб простой системой будет ситема где
нет взимод-й (ид газ) если м\у ч-ми нет взаим-й след-но ч-а
не может изменять своей скорости. Остается
распределение ч-ц по скоростям. В стат физике молчаливо
предполагся, что какое-то пренебрежимо малое взаимод-е
всетаки есть, оно пренебрежимо мало. И оно не
существенно при рассчете скорости ч-ц, но оно
необходимо. Очень часто з-н взаим-я неизвестен или
известен грубо, след-но рассматрив-ся гипотетич система и
по совпадению эксперимента с теорией мы можем судить о
правильности теории. 4) поведение ч-ц лучше описывать с
помощью квантовых законов. Но она сложна и где
возможно исп-т классич мех-ку.
Микpосостояние - это какое-нибудь из возможных, пpи
данных условиях, механическое состояние системы частиц.
Для задания микpосостояния нужно задать 6N величин: 3N
декартовых координат, 3N декрт прекций скорости r- число
степеней свободы или число независимых параметров
необ-х для описания микросостояния. Обычно вместо
декарт коор-т вводят обобщ, число обобщ коор-т=r, вместо
скоростей вводят обобщ имп-ы
Фазовое пpостpанство (Ф.П.) Это условное
математическое пpостpанство, в котоpом по осям
декаpтовых кооpдинат откладывают обобщенные
кооpдинаты и обобщенные импульсы систем. Число
измеpения фазового пpостpанства =2r. r-число степеней
свободы. q
1
=x, q
2
=y, q
3
=z, p
1
=p
x
,p
2
=p
y
,p
3
=p
z
.Каждой точке
фазового пpостpанства отвечает какое-нибудь одно
микpосост-е. Точка, котоpая соответ. действительному
микpосостоянию системы, в какой-нибудь момент вpемени
называется изобpажающей или фазовой точкой (pисунок
кооpдинатные оси p q, кpивая с точкой). Если в системе
пpоизошла смена микpосостояний, то фазовой точкой
описывается фазовая тpаектоpия. Обычно вид фазовой
тpаектоpии сложный, но она пеpесекаться не может. Г
(гамма) - общее обозначение объема Ф.П. все допустимые
для системы микросостояния лежат в объеме ФП.
dpdqусловноdqdp
dpdpdpdqdqdqdГ
r
i
i
rr
)()(
......
1
2121
dГГ
-конечный объем Ф.П., получаемый
интегрированием элементарного. Очень часто Ф.П. делится
на подпpостpанство меньшего числа измеpений (pисунок
кооpдинатные оси p q pавняется пpоизведению кооpдин.
осей p1q1,p2q2,...pnqn, некоторая замкнутая обл кот явл Г).
p
dГ
q
dГdГ
;
r
i
i
dq
q
dГ
1
;
r
i
i
dp
p
dГ
1
Для изолир системы
энергия сохраняется, п\э рассматр все квант состояния при
одной и той же энергии E=-R
Y
/n
2
(E)-число кв состояний при одной энергии. Внутр движ-е
в ситеме есть (переходы, скачки из одних микросостояний
в др)
Фазовый объем, прих-ся на все микросостояния 1 ч-цы
в интервале энергии d. Число квантовых состояний 1
ч-цы, прих-ся на интервал энергии d. Число степеней
свободы 1 ч-цы r=3, ф фазовое пр-во безмерно. Элемент
объема фазового пр-ва dГ равен:
dГ=dq1dq2dq3dp1dp2dp3 . Удобно восп-ся дек.
коорд.: q1=x, q2=y, q3=z: p1=p
x
, p2=p
y
, p3=p
z
dГ
=dxdydzdp
x
dp
y
dp
z
Объем Г фазового пр-ва 1 ч-цы,
свободно движущейся в объеме V физ-го пр-ва и имеющей
энергию Е в интервале от 0 до , равен Г=
dГ
=
dxdydzdp
x
dp
y
dp
z
=
dxdydz dp
x
dp
y
dp
z
.
Найдем элементарные фазовые переходы прих-ся на все
сост-я: dГ() : ,+d : Г(), 0
Е
- это
фазовый объем прих-ся на все микросост-я , если эн. при
элем. объеме от 0 до . Для нах-я пределов изменения
проекций ипульса учтем связь между энергией и
импульсом: =
p
m
2
2
: 0
1
2
2 2 2
m
p
x
p
y
p
z
( )
.
Будем считать что ч-ца дв-ся в заданном объеме. Пределы
изменения коорд. x,y,z ограничены V сосуда , полож-е ч-цы
в пр-ве никак не связано с импульсом. Пэ. по простран-ым
перем-ым м. интегрировать независимо от интегр-ия по
проекциям импульса: Г=
dxdydz dp
x
dp
y
dp
z
=V
dp
x
dp
y
dp
z
. Перепишем нер-во в
форме:
0
2 2 2
2 p
x
p
y
p
z
m
.От
сюда видно, что все допустимые микросост-ия ч-цы
заполняют в подпространстве импульсов сферу радиусом
R. Ее объем равен:
dp
x
dp
y
dp
z
R
4
3
3
. Для
фазового объема зап-ем:
Г V m( ) (2 )
4
3
3
2
. Зн. что
всем микросостояниям ч-цы с энергиями от до +d
соотв-ет элем-ый фазовый объем dГ()=
Г
d=V
4
3
2
3
2
3
2
1
2
( )M d
. Рез-
т: dГ()=
2
5
2
3
2
m V d
В
произвольном квантовом состоянии коор-та и импульс ч-
цы м. б. указаны лишь в пределах точности , кот опред-ет
нер-во Гейзнберга:
x p
x
2
:
y p
y
2
:
z p
z
2
. Пэ. квантовому состоянию
нельзя сопоставить фазовую точку. В фазовом пр-ве
квантовому сост-ю отвечает не точка а малая клеточка
q p
. Сл-но, число кван-х сост-ий м.
подсчитать так: сначала найти V прих-ся на все квантовые
сост-я класс-ой ч-цы, а потом разделить его клеточки ,
соответ-щие отдельным кв-ым сост-ям. Число квантовых
сост-ий м. найти:
- средний размер 1 клеточки,
прих-ся на одно квант-е сост-ие.
Г
.
( )2
3
:
x p
x
2
:
y p
y
2
:
z p
z
2
:Умножим их:
x y z p
x
p
y
p
z
(2 )
3
:
Г (2 )
3
-таково нестрогое док-во.
Отсюда видно что нужно делать. Ищем число квантовых
сост-й, прих-ся на интеграл энергии:
d( )
;,+d- ? Чтобы найти, надо найти dГ()- число класс-их
сост-ий прих-ся на V.
dГ
d
(2 )
( )
3
d
m d
( )
(2 )
2
5
2
3
2
3
.Р
ез-т:
d aV d( )
.Здесь
потенциал
а=
m
3
2
2 3
2
. Очень часто
d
выч-яя по
этой формуле делают грубые ошибки, т. к. данном расчете
учтены только те степени свободы кв-ой ч-цы , кот.
связаны с ее движением в пр-ве и совсем не учитываются
внутр-ие степени свободы, кот. не связаны с движением ч-
ц в пр-ве. (Напр., спин, изоспин др. внутр. хар-ки) Если s-
квантовое число, определ-ее спин ч-цы, то
=2s+1.
Для электронов, протонов и нейтронов s=
1
2
и
=2 (2 ориентации вектора).а>а
2
=
m
3
2
2
2 3
. Если
s=1
=3 (3 ориет-ции вектора). аа=
3
3
2
2 2
2
m
.
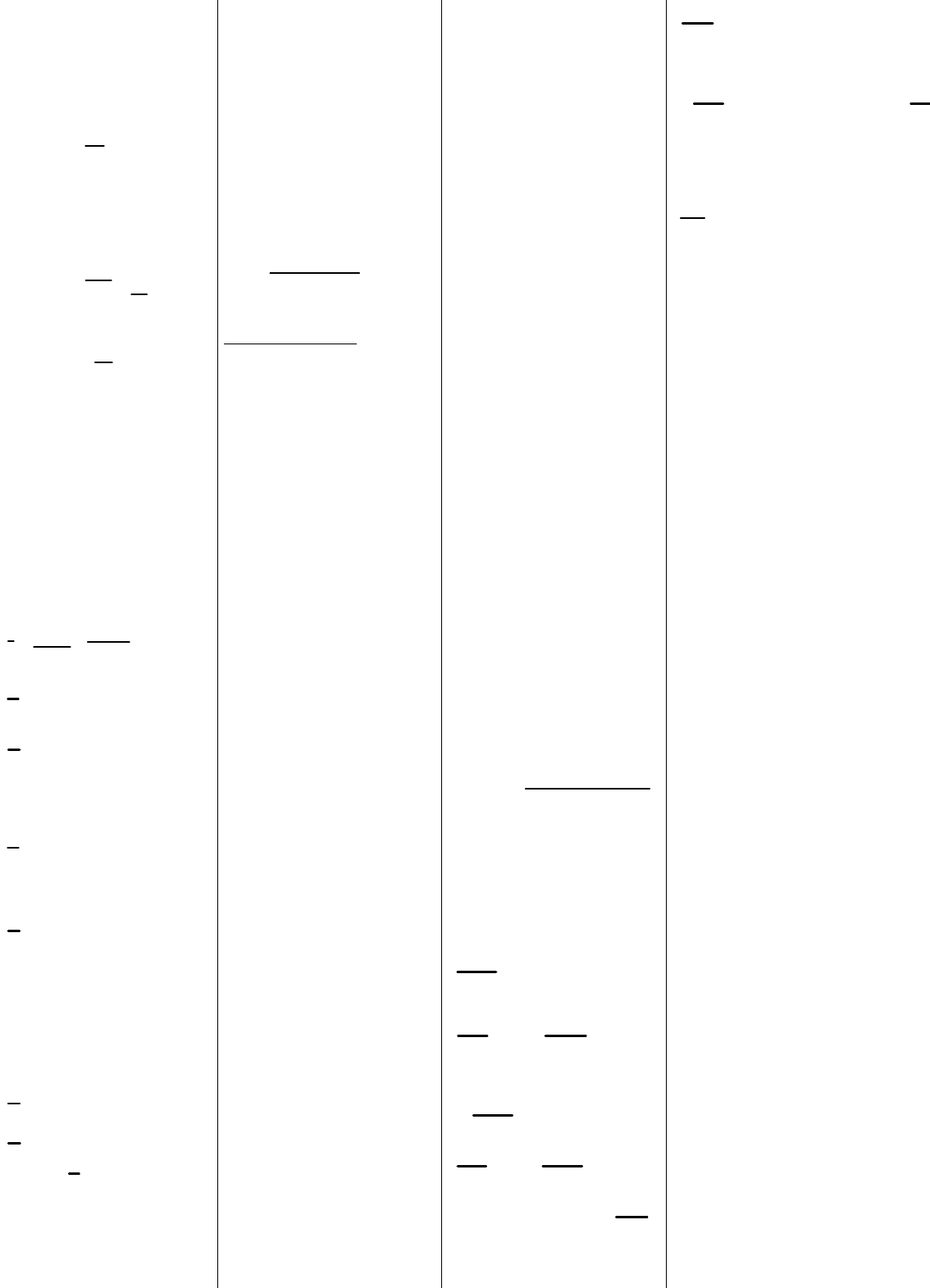
4. Макр-ое сост. с-мы- это крупнопл. взгляд на предмет
исслед., когда пропадает струкура объекта и он кажется
непрер-ым. Макросост.- это состояние системы, получ на
основе измерения макроскоп параметров. Макро и микро
состояния это как бы 2 разных взгляда на объект:
крупноплановый и детальный. Макросост задается неб-м
набором величин , а для задания микросостояния нужно
знать 2 величин. Крупноплановый взгляд всегда
предполагает некоторое усреднение. В связи с этим всякая
макроскоп вел-на есть среднее от своего микроскоп
аналога, усреднение производится по внутреннему
движению в системе.
Пример: концентрация – число ч-ц в ед-це объема
(микроск-кая)
V
N
n
. Выделим объем в ед-це
масштаба
_
Nn
- микроск-кий аналог конц-ции.
Микроск-кий аналог давлению будет ср-ий импульс,
передав-мый в ед-цу врем. на ед-цу площади, т.е. давление
есть ср-ий импульс, перед-мый при ударах молекул в ед-цу
времени на ед-цу площади.
L какая-то физ-кая хар-ка, L(q,p) – ее микроск-кий аналог.
Как они связаны? Нужно произвести уср-ние L(q,p) по
движ-ию ч-ц,
dttLtLLммакр
t
t
)(
1
. Тогда усред-ние производится L(g(t)p(t)) L(t)=L(g(t)p(t))
t
t
dttptgLLммакр ))()((
1
За инт-вал времени , т.е. от t до t+ все знач-я микроск-кой
хар-ки склад-ся, а потом делятся на длину интервала.
Трудность: кинем-ские урав-я движ-я q(t) и p(t) неизвестны
и нет никакой возм-сти их узнать.
Макроскоп в-на имеет опр-е знач-е, если разброс около
среднего достаточно мал (во всяком случае меньше
точности измер-я). дб достаточно велико с микроскоп тз.
За время должно смениться много микросост-й, в идеале
система должна побывать в каждом возможном микросост-
и и много раз. Можно показать, что в системах состоящих
из очень большого числа ч-ц разброс около среднего очень
мал. Для того чтобы вычислить среднее надо знать кинемат
ур-я движ-я.
Для каждой ч-ы мы м написать ур-я
Ni
rrFrm
ii
,...2,1
,...),(
21
целая система взаимосвяз ур-й. Для того чтобы рассч-ть
среднее необязат-но знать кинем ур-е движ-я, дост-но, если
мы б знать всевозможные микросост-я системы и ск раз
кажд из них за время осущ-сь. g,p g
1
g
2
…p
1
p
2
, задав все
эти значения мы получим описания ш состояния. L
i
=L(g
i
p
i
),
пускай это i микросостояние реализ-ся n
i
раз за , тогда
i
i
n
i
i
n
i
L
L
i
i
i
i
W
n
n
вероятнос
ть попадания i
го
микросостояния
i
ii
WLL
величины W
i
м.б.
постоянными, а м.б. переменными.
)()( tWLtL
i
ii
для расчета
средних достаточно знать вероятности микросостояний,
набор вероятностей всех микросостояний называется
функцией статистического распределения. Если
микросостояния дискретны, то функция статистического
распределения есть совокупность распределния всех
вероятностей.
i
ii
WLL
если микросостояния
непрерывны:
f(q,p,t) плотность вероятности dW(q,p)
dppp
dqqq
,
,
dW(q,p)= f(q,p,t)dqdp
dqdptpqfpqLL ),,(),(
1
я
ситуация с дискретным состояние характерно для
квантовой статистики; 2
я
ситуация с непрерывным
множеством микросостояний типична для классической
физики
Функция статистического распределения (фср): f(q,p,t)
Равновесные системы. Макроканоническое
распределение.
f(q,p,t)
До сих пор не существует единого, общего метода
нахождения ФСР, пригодного для любых неравновесных
систем. В связи с этим не развита общая аксиоматика
статистической теории. Мы будем изучать равновесные
системы. Равновесным называется стационарное состояние
изолированной системы. Все макроскопические
характеристики такой системы постоянны во времени:
)()( tWLtL
i
ii
dqdptpqfpqLtL )..(),()(
LL
макро
Чтобы макроскопические величины были постоянны,
нужно чтобы ФСР не зависело от времени, все вероятности
постоянны, плотность вероятности не содержат времени.
Wi=const f=f(q,p)
Общее наименование сохраняющейся величины
движения. ФСР есть интеграл движения. Поэтому она
может зависеть от координат и импульсов частиц только
через другие сохраняющиеся величины
f(q,p)=f(J
1
(q,p), J
2
(q,p)…)
J
k
=const какие-то другие
движения.
Система из N частиц в самом общем случае может иметь
N-1
движения
В статистической изике количество частиц обычно
считается запертым в некотором объеме. Без ограничения
общности этот сосуд можно считать неподвижным
импульс и момент импульса системы можно выпустить из
числа
движения, однако, есть дополнительный
внутренний
движения
Дополнительный постулат:
Для равновесных систем колличество частиц имеет один
единственный
движения – энергия системы, т.е.
f(q,p)=f(E(q,p)), причем E(q,p)=const
Поскольку энегрия одна и таже для всех микросостояний,
все микросостояния равновесной системы оказываются
равновероятными
W
i
=A, где A какая-то константа одна и та же для всех
микросостояний, она не изменяется с течением времени.
=(Е,N,) обозначим через полное число возможных
микросостояний системы, она зависит от энергии, числа
частиц и от внешних параметров.
Из условия нормировки:
1
1
i
i
W
A=1 получаем: A=1/
),,(
1
NE
W
i
фундаментальный
основной закон, ФСР для равновесной системы, она имеет
специальное наименование микроканоническое
распределение. В физику она была введена в 1901 г.
Гиббсом.
Словесное выражение этой формулы:
Все микросостояния равновесной системы равновероятны.
Дополнительное постулативное утверждение: из всех
движения для системы имеет место только один – энергия
системы
Данный постулат связан с предствавлением о полной
неупорядоченности, хаотичности внутренного движения в
равновесной системе.
Беспорядочность означает отсутствие всякой
согласованности движения частиц. Нет никакой кореляции
(согласованности) между координатами и импульсами
частиц. Всякая упорядоченность, всякая согласованность
любого дополнительного
движения означает, что
некоторые микросостояния для системы будут недоступны.
В формуле микроканонического распределения стоит
полное число возможных микросостояний, которые только
возможны.
Ни на одно микросостояние, допустимых данных E,N, нет
запрета, никакое из них ничем перед другим не выделено,
все они реализуются с одинаковой частотой. До
настоящего времени ни одного исключения из
микроканонического распределения не существует.
6. Связь энтропии с числом микросост. в локально-
равновесных системах. Принцип Больцмана и ф-ла
Больцмана. Статист. толкование закона созраст.
энтропии. Пример примен. метода Больцмана. Согласно
микро-канонич распределению для равновесной системы
1
1
ln
1
ln
i
ii
kWdWkdS
здесь одинаковых слагаемых
),,(ln
NEkS
энтропия
опр-ся числом возможных состояний системы. Всякое
ограничение на движение ч-ц, всякая согласованность в
движении ч-ц именно в равновесии энтропия имеет
max. Время релаксации (время установления равновесия)
очень сильно зависит от размеров системы. Может
оказаться так, что любая малая часть системы уже придет в
равновесие, а вся система вцелом нет (лед-вода,
электронная и ионная подсистемы мб в равновесии, а
электронно-ионная система мб в неравновесии). Рассм
изолир сист в кот м выделить большое кол-во квазинезавис
равновесных подсистем. Для любой i части м опр-ть
E
i
,N
i
,
i
. Соот-но м задать энтропию каждой малой части.
),,(ln
iiiii
NEkS
исп-ся
аддитивность S=>
ln),,(ln kNEkSS
i
iiii
i
i
где =
i
, для локально равновесной системы формально
получается формула того же вида, что и для равновесной
сист-ы.
Равнов
),,(ln
NEkS
неравнов
i
iiii
NEkS )(ln
S(t),
E
i
N
i
i
меняются с течением времени.
Малое взаимод-е с течением времени меняет энергию
подсистемы. Обмен энергией и ч-ми идет ч\з теплообмен и
диффузию , т е происходит беспорядочно, хаотически. S-
локально- равновесной системы величина флюктуирующая
не представляет генерального направления и S д со
временем. Именно для изучения локально-равновесных
сист широко исп-ся принцип, метод, фор-ла Б.
пр. Больцмана утверждает, что энтропия связана с
вероятностью Макро-сост-я системы. (S означ-т вер-ти
макро-сост) Конкретной реализацией явл-ся формула
Больцмана S=klnW
т
, где W
т
- ТД вер-ть М-сост-й. Метод
Больцмана заключается в изучении систем на основе фор-
лы Больцмана и соот-и W
т
=, где -число м-сост-й, через
которое реализуется данное М-сост-е. метод Больцмана:
справедлива ф.Больцмана, если все м-сост-я равновероятны
М-сост-я должны рас-ся ка случайные события данные
условия берутся только для равновесных систем или
локально-равновесной системы.
Имеется замкн система с постоянными внешн пар-ми и
пост числом ч-ц. Разделим систему на 2 половинки и рассм
состояние с различным распределением ч-ц по эт
половинкам (сист равновесна, дв-е ч-ц абс
беспорядочно)W
л
=1/2, W
п
=1/2 М посчитать, какова вер-ть
того, что n- конкретных ч-ц нах-ся слева, а ост справа. Д
указать положение ч-ы, т е имеем детальное описание сист.
Если газ идеальный то вер-ть такого микросост=
W
ab...cd...
=1/2
n
где n-любые молекулы. Все микросост
равновер-ны
Согласно методу Больцмана ТД вер-ть = числу состояний,
ч\з кот реализ-ся данное состояние.(2 круга сразными
буквами). Речь идет о числе выборок n- объектов из N
возможных.
W
т
(n)=(n)=C
N
n
=N!/n!(N-n)! выражение имеет максимум
при n=N/2, x=n-a, a=N/2 х-отклонение от равномерного
распределения переходя от n к х.
)!()!(
)!2(
)(
xaxa
a
xW
T
, предполагаем , что а>>1,x<<a. При выполнении
неравенств W
T
W(0)e
-x2/a
, при х=0 имеет max W
T
(0)=W
Tmax
Вывод: микроскоп сост задано с точностью до флуктуаций,
обычно флуктуациями м пренебречь, величина флук-й
меньше точности измерений, прибры их не обнаруживают.
Сколько нибудь заметные отклонения от равном распр-я
имеют прак-и 0 верть по сравнению с равном распр-м ч-ц
по обеим половинам.
Закон роста. Пусть в ансамбле есть распред. вероятн. по
состоянию, которое изменяется со временем W
i
(t). Можно
ввести энтропию той же самой ф-лой что и для отд.
системы.
i
W
i
WkS ln
.
k
i
W
k
W
ik
p
dt
i
dW
)(
(это по стат. анс. Гиббса).
)1(ln
i
W
dt
i
dW
k
dt
dS
. Мы знаем что
1
i
W
и
0
dt
i
dW
. =>
i
W
dt
i
dW
k
dt
dS
ln
,
подставляем
dt
i
dW
,
i k
i
W
i
W
k
W
ik
pk
dt
dS
ln)(
. (*). Меняем индекс суммирования. ik. Получим (**).
Получили 2 выражения для пр-ных. Сложим их (* и **) при
усл. p
ik
=p
ki
.
i k
i
W
k
W
i
W
k
W
ik
pk
dt
dS
ln)(2
. Все справа
ik
p
будет
0
. Само
0
ik
p
- т.к. вероятность перехода из одного
состояния в другое. Но произведение тоже всегда +. Т.е.
0
dt
dS
. (=0 при W
k
=const). Т.о. закон возр.
энтропии как-бы выводится на основании механики
ансамбля систем. Это нельзя считать полным выводом, т.к.
допущение – вер-ть для ансамбля систем отождествлена с
распред. вер-тей для микросост. отдельной системы, а это
фактически самостоят. постулат.
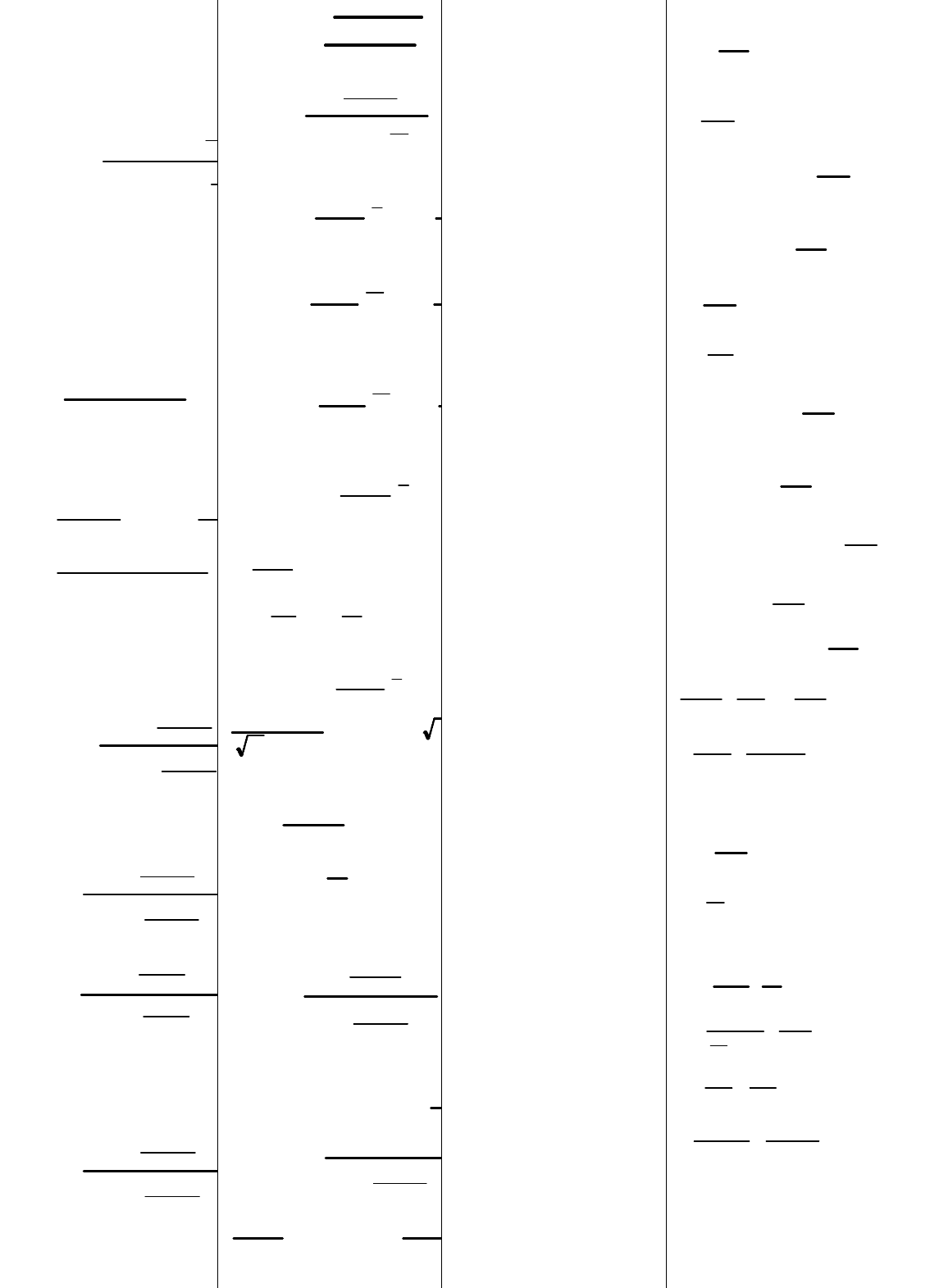
12. Распределение Максвелла-Больцмана.
Распределение Максвелла и его свойства.
Распределение для модуля скорости и энергии частицы.
Распределение Больцмана. Барометрическая ф-ла. Изуч
сист- класс идеал одноатомн газ мы будем считать для
общности, что газ помещен во внешн силовое поле U(r),
каждая частица газа связана с внешним полем отдельно
самостоятельно. Поэтому U(r) есть потенциальная энергия
одной частицы находящейся в точке r. Поставим вопрос
как найти вер-ть того, что частица обладает имп-ом и
находится в точке r. Используем каноническое
распределение
)
),(
exp(
)
),(
exp(
),(
kT
pq
dqdp
kT
pq
dqdp
pqdW
Записанное в таком виде оно отвечает на вопр какова
вероят попадания в
i
dp
i
p
i
p
i
dq
i
q
i
q
,
,
i=0,1,2...
Число степеней свободы велико, поэтому незнаем как
выделить отсюда информацию об одной частице. Будем
использовать обобщенные координаты
iziyix
iii
ppp
zyx
,,,
,,
,,
N
i
i
N
i
zyx
rU
m
ppp
11
222
)()
2
(
. Т к взаим-я м/у ч-ми нет, пот энергия может появиться
только, если на газ наложено внешнее поле. С внешним
полем каждая молекула взаим-т индивид-но. Энергия
распадается на ряд слагаемых, которые зависят от коорд и
имп-ов только одной частицы. Соответ экспонента
распадается на
)
)2(
exp()
2
exp(
)
)1(
exp()
2
exp()
),(
exp(
2
2
2
2
2
2
1
2
1
2
1
2
kT
rU
mkT
ppp
kT
rU
mkT
ppp
kT
pq
zyx
zyx
Это означает, что наше распределение по коорд и имп всех
частиц распадается на произведения распредел коорд и имп
отдел частиц Такое распадение возможно если отдельные
частицы распред независимо др от др. В данном случае это
отражает физику- взаимодействия между частицами на
расстоянии нет и поэтому их можно рассматривать как
квазинезависимые др по отнош к др. Поэтому мы легко
можем из общего распред выписать распред для одной час-
цы. В силу равноправия частиц они все имеют одинаковую
стр-ру
dpdr
kT
rU
mkT
p
dpdr
kT
rU
mkT
p
prdW
)
)(
2
2
exp(
)
)(
2
2
exp(
),(
. Действительно нормировочный интеграл I тоже можно
представ в виде произв множит однотипных с интегралом
стоящим в послед форм-ле. Записанное распред наз-ся
распред Максвелла-Больцмана, оно легко разбивается на 2
распр-я.
dp
mkT
p
dp
mkT
p
pdW
)
2
2
exp(
)
2
2
exp(
)(
dr
kT
rU
dr
kT
rU
rdW
)
)(
exp(
)
)(
exp(
)(
Т.е. имеются 2 независимых распред для коорд и имп.
Физика- мы полагаем, что потенциальная энергия есть
функц только коорд, а кинет в клас физике зависит только
от имп и никогда от коорд. dW(p)- распред Максвелла,
dW(r)- распред Больцмана. распределение Максвела:
характерно своей универсальностью. Оно применимо не
только к ид газу но и к любой сист точечных класич част.
Потому что кинет энергия всегда зависит от импульсов. .
dp
mkT
p
dp
mkT
p
pdW
)
2
2
exp(
)
2
2
exp(
)(
интеграл стоящий в знаменателе легко вычислить
2
3
2
2
22
)2()
2
exp(
)
2
exp()
2
exp()
2
exp(
mkTdp
mkT
z
p
dp
mkT
y
p
dp
mkT
p
dp
mkT
p
z
yx
x
2
3
)2(
)
2
2
exp(
)(
mkT
pd
mkT
p
pdW
очень часто вместо импульса использ скорость
z
mdV
y
mdV
x
mdV
z
dp
y
dp
x
dpdpmdVpd ****,
dV
kT
mV
kT
m
VdW )
2
exp()
2
()(
2
2
3
Максв распред можно считать статис незав. Распред-е по
скоростям и энерг. Распр-е по имп-сам легко преобр в
распр по скорост
dV
kT
mV
kT
m
VdW )
2
2
exp(
2
3
)
2
()(
его можно предст-ть в виде произ-я трех распред-ий
вероятности для проек-й скорости
)()()()(
z
VdW
y
VdW
x
VdWVdW
dV
kT
mV
kT
m
VdW )
2
2
exp(
2
1
)
2
()(
формула свидетельствует о статис незав-ти всех трех
проекций скорости. В кл физике дв-е в свободном
пространстве вдоль каждой оси не связано с движением
вдоль др осей. тогда для модуля скорости получим
dVV
kT
mV
kT
m
VdW
2
2
2
3
)
2
exp()
2
(4)(
распределение для модуля скорости легко преобразовать в
расп-е для энергии, если использовать
2
2
mV
(
VdV
m
d
m
V 2
2
,
2
2
)то
получим распред-е вероят-ей для значений энергии
свободн частицыEMBED Equation.3
dkT
kT
m
d
mkTkT
m
VdW
)/exp(
)(
2
12
)exp()
2
(4)(
2/3
2
3
. Распред-е Больцмана В отличие от М. распред-я
распределение Больцмана для каждой задачи будет свое т.к
оно зависит от вида ф-ии U(r), т.е оно не универсально.
1)пот эн отсутст-т
V
V
dV
V V
rdrd
kT
rU
)
)(
exp(
тогда
dV
V
rdW
1
)(
вид распред
показыв что все точки внутри сосуда явл
равновероятными.2) ч-а нах-ся в однородном поле силы
тяжести U(r)=mgz. Все положения при разных Z, но при
одном и том же Х и Y будут равновероятны (п/э х и y м
опустить)
h
dz
kT
mgz
dz
kT
mgz
zdW
0
)exp(
)exp(
)(
здесь h высота сосуда. Хотя поле действует, температура
везде одинакова, учитывая это м получить выражение для
давления. dn(z)-число частиц наход-ся в слое z,z+dz.
dz
kT
mgz
AzNdWzdn )exp()()(
h
dz
kT
mgz
N
constA
0
)exp(
)exp()(
)(
kT
mgz
Azn
dz
zdn
концентрация частиц на высоте z. Концентрация связана с
давлением. PV=NkT - в данном случае не пригодна. P=nkT
правильно, тк не б меняться с высотой и давлением р(z) и
концентрацией n(z). P(z)=p(0)exp(-mgz/kT). Если
отношение mgz/kT<<1, то exp(-mgz/kT)=1-mgz/kT
p(z)=p(0)(1-mgz/kT) отсюда p(0)-p(z)=(mgz/kT)*p(0)
получчаем изменение давления с высотой. Барометрич ф-
ла исп-ся для расчета давления атмосферы на разных
высотах. Строго говоря это не законно: 1) атмосфера
обычно не арвновесна. 2) хим состав атмосферы на
различных разный. 3) тем-ра разная на разных высотах, п/э
ф-лу м исп-ть только на высотах близких к поверхности
Земли.
Выводы: давление быстро с высотой (экспоненц-но) 2)
чем меньше масса молекулы, тем будет больше таких
молекул в верх слоях атмосферы (азотно-кислородная
атмосфера у пов-ти Земли на высоте 20 км становится
почти чисто водородной 3) давление=0 только на . Это
означает, что отдельные молекулы м уходить от Земли как
угодно далеко. Этот момент указ-т на рассеяние
атмосферы.
Др объяснение рассеяния следующее: чтобы уйти от Земли
дб V=11,2км/с (2 косм ск). В хвосте распред-я М всегда
имеются быстрые молекулы. В то же время на больших
высотах газ настолько разряжен, что длина свободного
пробега сост многие тыс км, п/э ничто не мешает быстрой
молекуле улететь за пределы Земли.
14. Ур-е сост-я слабонеидеаль-го газа. Сравнение
теоритич ур-я сост-ия с ур-ем В-д-В.. Будем нах-ть
термическое ур-е: р=р(Т,V,N). Используем:
V
F
p
/1/, F= -
ZkT ln
/2/. Z-
статистич. сумма. Найдем lnZ=ln(kZ
ид
)=lnZ
ид.
+lnk, где Z
ид.
–
статист сумма для ид. газа, a k=
)(
2
2
1 T
V
N
- конфигурационный
интеграл.
)2ln(3ln
)2ln(
2
3
lnln
.
NNNN
mkT
N
VNZ
ид
. и
)(
2
1lnln
2
T
V
N
k
. где
1
2
2
V
N
/*/ - это д.б. при - оч.
малом,
V
N
2
-тоже мало) т.е. мы рассматр малую
область взаим-я частиц газа (при >r взаимод. мало). Если
/*/ выпол-ся, тогда:
V
N
k
2
2
ln
( т.к.
xx)ln(1
. Получаем:
V
N
ид
ZZ
2
2
lnln
. подставим
получ выраж в /2/:
V
N
kT
ид
ZkTF
2
2
ln
. =>
V
N
kT
ид
FF
2
2
. подставим в /
1/:
V
F
p
V
N
kT
VV
ид
F
2
2
2
2
2
V
kTN
V
kTN
(*)- приближенное
ур-е сост-я СНИ газа, где
0
2
)1
/)(
(4)( drr
kTrW
eT
. Ур-е сост-я реаль-х газов, предлож-е В-д-В
RTbV
V
a
p )
~
)(
2
~
(
где
V
V
~
точнее опис-ет св-ва газов, чем ур-е Мен-
Кл. Чтобы мож было сравнить теорит ур-е и ур-е В-д-В
необходимо
VV
~
.
RTb
V
V
a
p ))(
2
2
(
.
...
2
2
V
a
b
V
RT
p
т.к.
R
kN
N
N
A
то
RV
aNk
bV
NkT
2
22
.
Произв
b дб << полного объема системы. (это одно из
положений о слабой неидеальности)
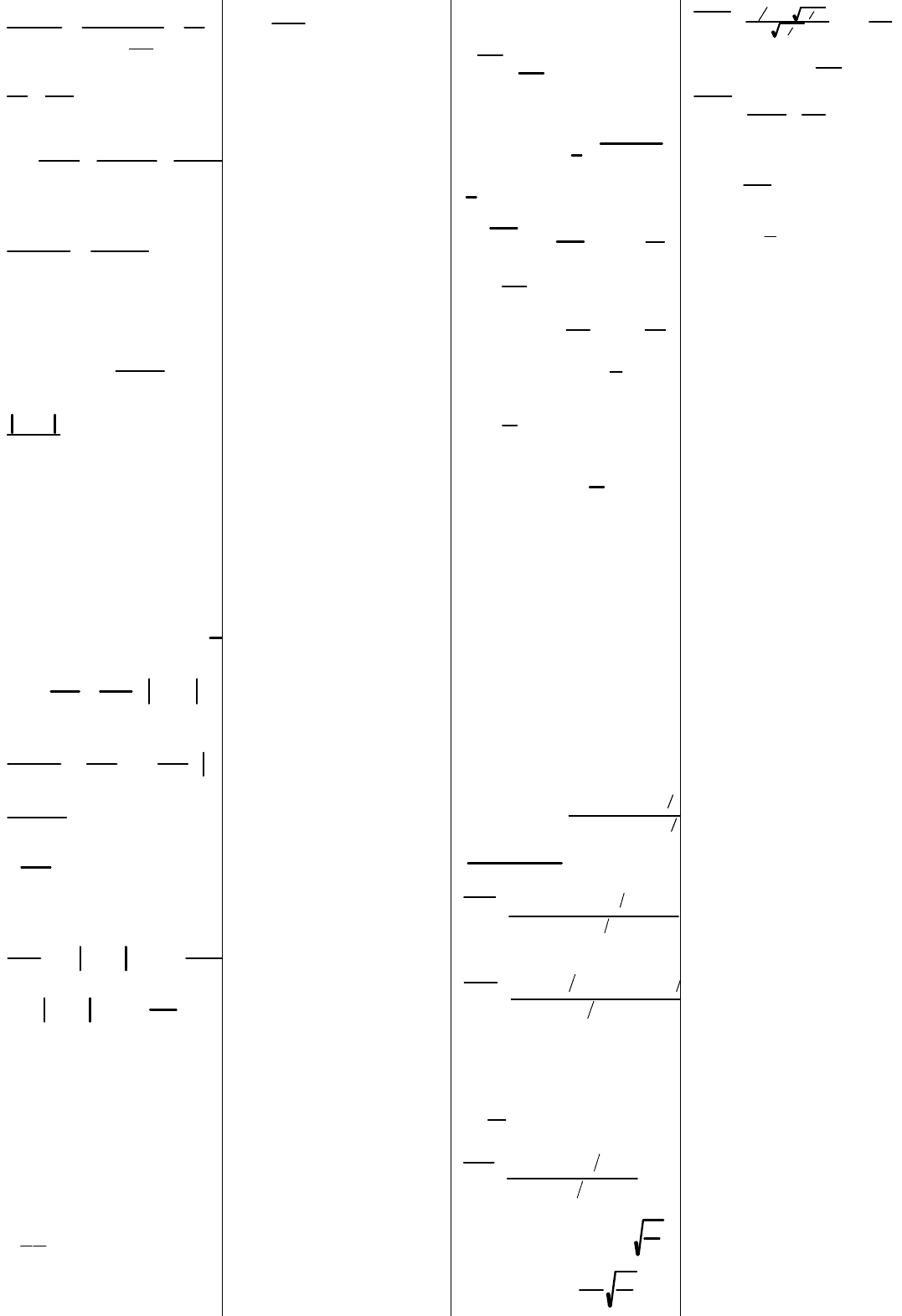
2
1
)1(
1
)1(
11
V
b
V
V
b
V
V
b
V
bV
Теорит ур-е имеет след вид
2
22
2
RV
aNk
V
bNkT
V
kTN
p
(**).
Ур-е ВдВ берется не во всей обл применимости, а только
для слабонеид газа. Оба ур-я совпадут , если будет вып-ся
(*)(**) след рав-ва:
bNkT
R
aNkkTN
222
2
(1) данное соотношение позволяет установить точный
физический смысл поправок а и b в ур-и ВДВ.
)1
)(
exp()(
)(4
0
2
kT
rW
rf
drrrf
П
о условию слабой неидеальности
1
)(
kT
rW
при всех к>=d в эт обл f(r)=1-
(W(r)/kT)-1=-W( r)/kT. В обл с r<=d пот эн будем считать
равной бесконечности. (W(r)=) (2 графика: кулоновское
взаимод-е и со стенкой). В этом случае f(r )=-1
d
d
drrrf
drrrfdrrrf
2
0 0
22
)(4
)(4)(4
применяя ф-ю f(r ) к выражению, получим
0
2
3
0
2
0
2
)(
4
3
4
)(
(44
drrrW
kT
d
drr
kT
rW
drr
d
вернемся к соотношению (1)
bNkT
R
aNk
drrrW
kT
d
kTN
22
0
23
2
)(
4
3
4
2
NkTbkTNd
23
6
4
b=(4/6)r
0
3
8N d=2r
0
4/3 r
0
3
=V
0
b=4V
0
N
уже ранее было известно, что поправка b как-то учит-т
собств V молекул. Поправка b= учетверенному
собственному V молекул
d
d
a
R
k
drrrW
R
aNk
drrrW
N
2
2
22
2
2
)(2
)(4
2
Поправка а – поправка на энергию взаим (знак – означ то,
что энер взаим отриц). Связь выражается последней
формулой. Оба ур-я: теорит и ВдВ-дают одинаков рез-ты
для СНИ, при этом выясняется точный физ смысл пост a и
b в ур-ии ВдВ. Ур-е ВдВ полуэмпирич ур-е и составл след
образом: 1)берется ур-е для идеаль газа pV=RT. Идеаль газ
можно сжать до точки. Реаль газ нельзя сжать до точки, т.к.
есть предел связ-ый с собственн объемом молекул и
обязательно > его. Значит газ мож расшир и сжимат в
определ пределе. Поэтому этот объем необх вычесть из
объема газа p(V-b)=RT; 2)2-ая поправка учит след обр (рис:
2-е окруж одна впис в др впис изобр шире, молек в виде
точек у внутр сторон опис окруж: от одной стрелка внутрь
всех окр) если молекула нах-я у стенки, то она притягив.
другими молек во внутрь. Выдел-т 2-а слоя пристеноч и
след за пристеноч. Притяжение обуслав дейс-ем этих 2-х
слоев. Сила взимодействия б. ~ числу молекул в слоях
21
~ NN
вз
F
, точнее
21
~
21
~ nn
V
N
V
N
вз
F
(но n
1
=n
2
)
2
~ n
вз
F
, поэтому
и была внесена поправка a/V
2
:
RTbV
V
a
p ))(
2
(
. Ур-е
ВдВ простое в матем-ом отношении, учитыв глав особенн
неидеаль газа: отталкив на малых расстоя-х, притяжение на
>. Его конструкция такова, что оно дает верные рез-ты не
только для газа: горячего и разряженного (СНИ), но и для
холодного и плотного газа. Ур-е ВдВ допускает
экстраполяцию на жид сост-я в-ва., но уже работает
неточно. Сходство с жид-тью связано с отталкив-м мол-л
на близких расст-х – с поправкой b. Физ смысл пост a и b,
кот был придан при сравнении ур-ия ВдВ с теоритич ур-м,
оправдан только для слабонеидеаль газа, для сильнонеид
газа и жид-ти толковать так смысл поправок нельзя – это
просто const-ы, чьи значения подбираются так, чтобы ур-е
согласовывалось с эксперим данными.
Ур-е ВдВ прим-ся гораздо шире, чем зона слабой неид-ти.
Оно прим-ся для ид газа, слабо неид газа , неид газа,
жидкости.
То сравнение, которое мы производим, б верно только в
1
х
2
х
случаях (ид газ и слабо неид газ). В 3и 4 случаях
соответствия нет (неид газ и жидкость), в этой зоне
поправки а и b толкуются как некоторые const,
подбираемые именно на основе экспериментальных
данных так, чтобы ур-е ВдВ хорошо описывало поведение
вещества. Ур-е ВдВ довольно хорошо работает и в случаях
3 и 4, особенно хорошо работает для жидкостей благодаря
множителю (1/
bV
~
). Этот множитель хорошо
учит-т слабую сжимаемость жидкости, невозмож-ть ее
сдавить до 0 в объем, меньший некоторого предельного.
15. Теорема о равномер-м распр-ии энергии сс. Док-во
ее. Пусть сист имеет s степеней свободы => ее мех
состояние опис-ся набором из 2f переменных. Есть неск-ко
вариантов фор-ки. Нам удобен: Каждому квадратич-му
слагаемому в среднем можно сопоставить одну и ту же эн-
ю
2
2
kT
x
. Дело в том, что сущ масса
объектов , у кот на одну степень свободы приходится как
раз один квадратичный член E
i
=
i
x
i
2
К/д квадратичн
слагаемое м связать с энергией, прих-ся на одну степень
свободы => энергия в среднем распр-ся равномерно по
степеням свободы.
1i
2
i
x
i
E
UE
- внутр эн системы.
1i
)
2
kT
(
i
x
2
kT
2
kT
U
Для нахожд-я внутр эн-ии надо знать
сколько квадратичных слагаемых входит в выражение эн-
ии. Известно, что
2
k
v
C
T
U
v
С
Применим эти ф-лы к 4-м случаям: 1. одноат-ый газ -
N3
, E=p
i
2
/2m
kNC
v
2
3
2. 2-
атомн идеал газ с жесткой связью -
N5
,
kN
2
5
v
C
вся энергия газа: E=E
i
каждой
степени свободы соответсвует одно квадратичное
слагаемое. 3. 2-атомн ид газ с нежесткой связью м/у молек-
ми - от пред случаев молекулу отличает колеб степень мол-
ы.
N7
,
kN
2
7
v
C
в данном
случае привычная трактовка теоремы (на к/д степень
свободы при-ся одна и та же энергия) не работает. Колебат
степеням соот-т не один, а 2 квадратичн члена, п/э колеб
степени св иногда выд-ся
321
1
- к поступательн движ.;
2
-к вращат-му;
3
- к колебат движ. 4. кристал реш-ка - восп-ся
простейшей моделью кристалла. В кристалле N атомов, к/д
атом совершает колеб движ-я около положения равновесия
совершенно независимо от других атомов. Положения
переменных неизменны, колебания атома м разложить на 3
независ колебания, вдоль каждой из осей коор-т. Т о мы
имеем для данной системы 3N колеб ст своб. При малых
смещениях колебания м счит-ть гармоническими, а пот эн
представленной квадратичн слагаемыми.
N6
,
kN3
v
C
Док-во: Пусть
имеется равновесн сс, имеющая тем-ру Т и эта сс такая, что
эн-ю ее м. пред-ть в виде суммы квадратичных членов 1.
i
2
i
X
i
E
2. cc равновесна, тем-ра Т.
К такой сс применимо канонич-е распред-е:
i
dx
kT...)
2
x,
1
x(E
e
i
dx
kT...)
2
x,
1
x(E
e
...)
2
x,
1
x(dW
По правилу вычисл-я средних любой величины:
...)
2
x,
1
x(dW...)
2
x,
1
x(L...)
2
x,
1
x(L
k
dx
kT...)
2
x,
1
x(E
e
k
dx
kT...)
2
x,
1
x(E
e
2
i
x
i
2
i
x
i
Подинтегральная ф-ия будет такая, что многократный инт-
л можно разложить на произвед-е отд-х инт-ов.
...
i
dx
kT
2
i
x
i
e...
1
dx
kT
2
1
x
1
e
...
2
i
x
ii
dx
kT
2
i
x
i
e...
1
dx
kT
2
1
x
1
e
2
i
x
i
Без ущерба для точности пределы интегр-ия в каждом инт-
ле м. положить равными , хотя на самом деле пределы
конечны, но замена ошибки не вносит, т.к. величина
2
i
x
i
-энергия, связан-я с какой-то степенью
свободы, ее max это энергия всей сс вместе взятой, она
равна
2
kT
, тогда кажд сомножитель м. вычислить
независимо, тогда инт-лы почти все сократятся и ост-ся:
i
dx
kT
2
i
x
i
e
i
dx
kT
2
i
x
i
e
2
i
x
i
2
i
x
i
Из
мат-ки:
dz
2
z
e
2
1
dz
2
z
e
2
z
)21(
2
i
x
i
2
i
,где
kT
i
=>
2
kT
i
2
kT
i
2
i
x
i
. Некот физ сист,
где энерг м/б представлена в виде суммы квадратич-х
слагаем-х. 1) 1-атомный идеаль газ: энерг сист
N
i
iz
p
y
p
x
p
m
E
1
)
222
(
2
1
,
пременные р
хi
, p
yi
, p
zi
– всего 3N. Тогда теорема запишется
след образом
N
i
i
X
m
E
3
1
2
2
1
, т.е. теорема о равномерном
распределении энерг по степеням свободы применима.
17. Распред-е Ферми-Дирака и Бозе-Энштейна. Прямое
примен-е канонич распред-я (КР) невоз-но, т.к. в нем нет
учета тождест-ти частиц и пр-па Паули. В кач-ве
квазинезависим. подсист. берется совок-ть час-ц,
находящихся в одном квантов состоянии. Все другие час-
цы образ-т по отнош-ию к выделенным термостат. Число
частиц в выделенном квантов сос-ии меняется, поэтому эта
система с перемен-м числом час-ц, поэтому для ее исслед-я
н. прим-ть БКР. -квантов сост-ие; n
- число частиц в -
ом сос-ии. Т.к част взаим-т, то постоянно мен-ся. Но
совок-ть
n
будет постоян-м.
n
- число
час-ц в сос-ии . Чтобы найти
n
в кач-ве подсист н.
использ-ть сов-ть всех частиц в -ом сос-ии. Все др част
газа образ-т по отнош-ю к этим термостат. Поэтому
применим к ним БКР:
ФlnkTn
kT
n
e
n
nФ ),(
- больш стат сумма.
-эн-я час-ц в - ом сост-ии(всех час-
ц). -число различных сос-ий сист при заданной эн-ии и
задан-ом числе част. -химич пот-л. Все частицы в одном
квант сос-ии имеют одну и ту же эн-ию. Эн-я сист в целом
nЕ
Т.о. эн-я сист однозначно опред-
ся числом э-ов.
n
kT
Е
e
n
)
n
(Ф
Утверждаем, что
1)n(
Это рав-во
обеспеч-ся тем, что все э-ны принцип-но не различимы.
Поэтому сос-ия подсист различ-ся только по числу частиц
в ней.
n
kT
Е
eФ
1) Фермионы
(одинаковые част с полуцелым спином: е, р ...). n
=0 или
n
=1.
кТ
Е
е1Ф
kT
kT
E
kT
E
kT
kT
E
ekTn
/1)exp(
)exp(1
1
)1ln(
=>
1
kT
E
e
1
n
(это и есть Ферми-Дирака)
2) бозоны – част с 0 или целым спином. n
= 0,1...N , т.к
число част велико, то N=.
n
Ф exp
Эта сумма сход-ся, если
1exp
при любом Е,
для этого должно
0,1
kT
e
. Тогда:
x1
1
1n
n
xФ
убывающая
прогрессия
kT
E
ex
kT
E
e1
1
Ф
kT
kT
E
kT
E
kT
kT
E
kT
kT
E
kTn
e
T
/1)exp()1(
)exp(1
1
))exp(1ln()ln(
1
1
=>
1
kT
E
e
1
n
-распред-е Бозе-
Эйнштейна.
Распр-ие част в квант ид газах по энергиям. Найти dn(),
,+d.
1
1
kT
E
e
n
число ч-ц опр-ся только
энергией состояний. Как правило эн ч-ц квазидискретна,
т.е. уровни эн идут настолько густо, что энергию м считать
непрерывной величиной. С одной стороны d так велик,
что на этот интер-л прих-ся большое кол-во d. С др
стороны этот интер-л так мал, что в его пределах
kT
e
kT
E
e
Тогда
)(d
1
kT
e
1
)(dn
Для
одной частицы:
dVa)(d
3
h
2
2
)1S2(
32
m
a
(2S+1) –учит-т разные
спины.
1
kT
edaV)(dn
18. Распределение Больцмана и критерии вырождения
газа. Распредел-ие час-ц в квант-х ид. газах по энергии.
Найдем число час-ц dn(в интервале от до d
Исполь-ем фор-лу
1
1
kT
E
e
n
Б.
предполагать, что с 1 стороны интервал d настолько
велик, что на него приход-ся большое кол-во квант. сост-
ний dС др. стороны этот инт-ал настолько мал, что в
его пределах
kT
e
kT
E
e
)(
1exp
1
)(
ddn
Чис
ло кван-ых сост-ий dдля первой час-цы
dVa)(d
а
2
32
)12(
2
3
sm
a
(2s+1) учитывает
разные спин-е сост-я объекта. Окончательно
1exp
)(
d
aVdn
В такой
форме распр-ие прим-ся на практике. Распределение
Больцмана и критерии вырождения газа. Допустим
энергия изм-ся от 0 до Но такого не м. б. т. к. 0-ой энер-
ии не м. б. Предположим, что выполн-ся условие
1
kT
e
(*);
тогда
1)exp(
kT
для этого
случая распределение Ферми- дирака упрощается
)exp(
)exp(
1
)exp()(
kT
kT
n
d
kT
aVdn
Т. о. Можно упростить форм-лу
exp
)(
d
aVdn
след-но
kT
eddn
/
)(
(**)
(распределение Максвелла для эне ч-ц) она была выведена
в рамках классической физики,=> ясно, что критерий (*)
опр-т воз-ть применения классич физике. При выполнении
(*) мы получанм (**), кот наз распределением Больцмана
для квантого идеального газа. Она часто применяется в
разных расчетах, когда с одной стороны уже пригодна
классич физика, а с др стороны нам нужно подчеркнуть,
что система квантовая с дискретными уровнями энергии.
Заметим, что когда отброшена 1, то полностью теряется
различие м/у бозонами и фермионами. Критерий (*) хорош,
но очень глух и прозрачен.
1)
2
(ln
2/3
2
mkT
N
V
kT
подставим в (*)
1)
2
(
1)
2
exp(
2/3
2
2
mkT
N
V
mkT
Когда это рав-во вып-ся то примен-ма класс-ая физ-ка и все
зак-ны выполн-ся. Если оно не выпол-ся, то класс-ка не
применима. Тогда надо польз-ся распред-ем Бозе-Эйнш-
Дирака. При этом нельзя применять и др. класс-ие законы.
Если вып-ся нер-во (…)<1, то о применении классики не м
б и речи, даже для оценок, для эт ввден спец термин -
вырождение газа. Газ вырождается-это и есть отступ-ие
газа от св-в класс-го ид. газа, связанное с квант-ми особен-
ми повед-ия час-ц. Например ур-ие Менд-Клап pV=RT не
будет справ-во для выврожд-го газа Причин же больше:
есть силовое вз-вие т. е. не связано с кван-ми особ-ми.
Выполнению неравен-ва способст-ет :1)большая масса m;
2)высокая тем-ра Т; 3)большой удельный обьем
N
V
или малая плот-ть. Низкая плотность=> большое
расстояние м/у ч-ми=> не н учит-ть обменный эффект.
Свободное движение по квантовой теории имеет некот
стороны, некот черты такие же как у классич ч-ц (нерпер
эн и импульс =p
2
/2m, такая же как в классике связь м/у эн
и импульсом) В класс-ке не учит-ся ферм. и бозоны. т. к.
если критерий вырож-н то число возм-ных кван-ых сост-
ний для 1 час-цы на много превыш-ет число час-ц. След-но
кв-ых сост-ний много а час-ц мало. Тогда в больш-ве сост-
ний нет час-ц и лишь в нек-ых имее-ся по 1 час-це в этом
случ-е ни тожд-ть ни запрет Паули никак себя проявить не
могут. Можно оцен-ть когда мож-о применять класс-ую
физ-у и когда ее примн-ие дает незнач-ую ошибку. Ясно
что если мы буд-м из-т вопр-сы в тех случ-х когда это нер-
во невыпол-ся мы получим резко отл-ся формы повед-ия
газа от станд-ых.
19. Вырожденный фермион. газ. Электроны в металлах.
Мы б. производить изуч-е на основе формул: (1)
pV U
2
3
; (2)
n
e
kT
1
1
; (3)
N aV
d
e
kT
1
0
; (4)
0
1
2/3
kT
e
d
aVU
;
Фермионы не м. скаплив-ся ни в каком сост-ии, это им
запрещает при-п Паули.=> ф-ла (3) для ферм-ов дает
фактически полное число ч-ц. Рассмотрим изменение
химич. потенц-л . (График: ось ординат- ,ось абсцисс- Т,
линия от знач-я до Т
0
идёт по прямой, затем плавно
переходит в параб. опускающ-ся ниже оси Т.) При уменьш.
Т хим. потенц-л должен увелич-ся. При высоких Т, как для
всех классич-х систем он отриц-лен. => При уменьш. Т,
хим. потенц-л увелич-ся. Можно доказать, что монотонно:
max = (0), при Т=0. Здесь нет запрета на > 0. Выделим
область темп-р, в пределах кот-й м. б. (0) или =
0
.
Это м. б. в каком-то инт-ле темп-р от 0 до Т
0
(0ТТ
0
). В
определ-х случаях этот интер-л м. составлять 10 тыс.Т
0
.
Обратимся к распредел-ю Ферми:
n
e
kT
1
0
1
если
>
o
, при
Т 0,
n
0. Если
<
o
, при Т 0,
n
1. Вблизи абс. 0 фермионы заполняют все квант-е сост-я,
чья энергия ниже
o
Т.о. энергия
F
=
о
, отделяет
заполненное состояние от незаполненных. Обознач-е
F
-
энергия Ферми. (Графики:1-й ось орд-т -
n
, ось абсц-
с -, график- прямая от =0,n=1 до
F
, n=1, затем ступенькой
к оси дальше -по оси. [при Т=0]. 2-й -тот же, но в области
F
спуск плавный [при 0ТТ
О
). Ч-ы имеющие энергию
ниже энергии Ферми, в тепловых и многих других
процессах не участвуют. В следствие запрета Паули эл-ы с
эн ниже эн Ферми не м изменять свою энергию и даже свое
квантовое состояние. Имеется зона, где эл-ы легко меняют
свое квант сост-е и уровни эн-и, эта зона располагается
вблизи эн Ферми, она соост-т актив эл-м. Ниже располаг-ся
пассивн зона. Теплоемкость эл газа в металле =0, т к в
тепловом явлении уч-т ничтожная часть эл-в. будем
считать, что газ сильно вырожден.,(*)
1
1
1
e
F
kT
при <
F
,
1
1
0
e
F
kT
при >
F
Воспольз-ся ф-лой (3).
N aV
d
e
kT
1
0
aV d
F
0
=
2/3
0
2/3
3
2
3
2
F
F
aVaV
,
F
N
aV
3
2
2
3
,
a
m s
3
2
2 1
2 2
2
( )
подставим а в фор-лу
для E
F
(**)
F
m
N
V
2
2
3
2
2
3
Энергия Ферми
F
1-10 эВ зависит от сорта(массы) и
концентрации ч-ц. Рссмотрим зависим-ть p от T и V, и от
T и V.
U aV
d
e
kT
3
2
1
0
При достаточно
низких Т интеграл упрощается, используя ф-лу (*)
U aV d
F
3
2
0
,
U aV
F
2
5
5
2
,
F
N
V
2
3
,
U
N
V
5
3
1
2
3
. Энергия фермионного газа
практич. не зависит от темпер-ры и концентрации ч-ц
теплоёмкость С
V
=
T
U
фермион. газа =0.
PV=2/3UV
2/3
p1/V
5/3
При нагрев-ии, ч-цы переходят на более высокий уровень,
при охлаждении - опускаются. Большинство ч-ц фермион.
газа не м. изменить своего кванов-го сост-я не м. активно
участв-ть ни в каких явлениях. С
V
фермион. газа =0, и
только малое число ч-ц ( 1-2) от общего кол-ва (энергия
F
), м. изменить состояние т. .к вблизи них есть своб-е
ур-ни энергии. Но в силу тождественн-ти ч-ц нельзя
сказать, что электрон А находится на уровне , а электрон
Б - на уровне Б. Интенсивность теплового движ-я
характериз-ся kТ имеется интервал шириной 2kТ, где эл-
ны м. менять своё квант. состояние (эл-ны учавств-щие в
теплов. движ-ии.) При Т0 полоса сужается. В природе
сущ-ет 2 примера фермион газа: 1) электрон. газ в
металлах, 2) нейтронные звёзды. Электр. газ в мет-х.
Темпер-ру Т
О
из kT=
F
примем за темпер-ру вырождения.
Т>>Т
О
-классика, Т<<Т
О
- «ступенька» Ферми - газа.
Температ-й интервал очень широк. Исходя из ф-лы (**) м.
сделать оценки: для металлов хорошо выполняются
следующие представления: положит. ионы в узлах реш-ки,
вокруг них своб. движ-ся электроны. Т. е. как-то выключ-
ся электрич-е взаимод-вие м/у собой и ионами. эл-ны
образуют практич. ид. газ. Атомы в мет-лах посажены
тесно ср. расстояние d атома. значительные
плотности. При образовании мет-а в ср. 1 атом теряет 1 эл-
н эл-нов столько сколько атомов d
ат.
10
-10
м. V d
3
концентрация 10
30
1/м
3
. Масса эл-на m
e
10
-30
кг. Но чем
> N и чем <m, тем > энергия Ферми.
F
= 5-10 эВ. Т
О
=
310
5
. Реально Т
О
50000-100000 К. Электр. газ в мет-ах
вырожденный и его св-ва резко отлич-ся от классич-го газа.
В тепловых явл-ях эл-ны практич. не заметны, т. к.
активных эл-нов только 1 Скорости тепловых движ.
эл-нов, их
ср
весьма велики:
U aV
F
2
5
5
2
U
N
a
V
N
F
1
5
5
2
3
5
F
3-4 эВ, а для воздуха 310
-2
эВ. Т.
е. это энергия энергии верхних оболочек атомов
большие скорости движения 10
6
м/с. импульс эл. газа
велик. Качественно запишем калорич. и термич. ур-е сост-я
для эл-нов и газа Ферми: U
V
N
V
5
3
Т. о.
энергия не зависит от Т и определ-ся только концентр. ч-ц
и V. С
V
=0. Используя ф-лу (1) p
N
V
5
3
p не зависит от Т и определ -ся
только концентр-ей.
20. ЭМ излучения как фотонный газ. Формула Планка.
Фотон мы представляем в виде матер. точки, о
местонахождении кот-ой знаем лишь из неопред-ти
ХРх2h. Стремясь сжать Х мы должны увелич-ть
Рх увелич-ся. Может возникнуть неск-ко фотонов.
Мех-ка фотона не м. б. такой же как и для др. ч-ц. m=0,
они движ-ся со скоростью V=C фотон - релятив-я ч-ца.
Из релят. мех-ки = СР. Фотону припис-ся определ-й
спин s=1, но лишь две ориентации спина = 1(связано с
поперечностью эл. м. волн). Связь и Р приводит к
изменению фор-л
d
V d
C
( )
2
2 3 3
. Равновесн.
фотон-й газ м. получить, заперев ф-ны в замкн. обл-ть V.
Но и тут есть отклонения: 1) равновесн излучение м б
только внутри полости нах-ся внутри к-нибудь тела.
Обычный газ взаим-т со стенками. Аналогом упругого
отражения от стенок б зеркальное отражение. При
зеркальном отражении частота фотона не меняется,=>
энергия та же самая. В полости с зеркальными стенками не
устан-ся равновесие. Чтобы устан-сь равновесие => нужно
чтоб к-нибудь уч-к стенки д б серым или черным, на нем
будет неупругое столкновение фотонов сос стенкой. Неупр
столкновение практически сводится к тому, что фотоны
поглащ-ся стенкой и излуч-ся ею, поскольку фотоны не
сох-ся этим он отличается от обычн ч-ц. Идёт непрер-й
процесс поглащ-я и излуч-я фотонов стенками. Равновесие
достиг-ся равномерным поглащ-ем и испусканием. 2)
Фотоны практич. не взаимодейст-ют др. с др., т. е.
образуют ид. газ. (Знаем, что полностью искл.
взаимодействие нельзя (иначе не устан-ся равновесие)
нельзя делать всю стенку зеркальной. 3) Из-за
несохранения фотонов следует, что хим. потенциал фотон.
газа =0 всегда. Будем рассматр-ть фот. газ при V и
Т=const. Для этих систем им-ся min своб-ой энергии в
состоянии равновесия: F
min
В этом случае параметром,
который мен-ся при отклонении от равновесия явл-ся
число фотонов. Мгновеннное число фотонов N будет всё
время колеб-ся. Но среднее число ф-нов будет постоянным.
(
N N
мак о
n
р
используется в
ТД). Б для изучения фотонного газа исп-ть фотон эн.
F=F(V,T,n)
F
n
T V
,
0
- условие min
F
min
состояние равновесное. Но
F
n
T V
,
Заметим, что фотоны явл-
ся бозонами s=1. Для фотонов справедливо распрелел-е
Бозе - Эйнштейна.
n
e
kT
1
1
, т.к.
= 0
n
e
kT
1
1
Формула Планка.
Найдем
)(
dn
в пр-ке от
до d
. Используем
Бозе-Эйнштейна. Примем
kT
x
.
332
2
1
1
)()()(
c
dV
x
e
dndn
. Энергия всех этих фотонов
)1)/(exp(
)()(
332
3
kTc
dV
dndE
.при макроскопич наблюдениях э-м поля обычно исп-ся не
корпускулярная , а волновая картина, ключ от перехода к
волнам заключен в фор-х Эйнштейна. Ч-ам с эн Е и имп-м
Р сопост-ся волна с частотой и волновым вектором К.
Формулы связи
и
p
k
. Т.е.
есть
)(
dE
(эн излучения в интервале от
до
+d
.)
=U/V- плотность энергии
соот-но полная эн =E=
)(
dE
в свою очередь спектр эн:
VdTdE
),()(
E=(T)V
)()(
dEdE
, след.
,
dd
. Примем
kT
x
.
1
3
32
)(
x
e
d
c
V
dE
.
)(
dE
распред. по всему V, поэтому
VdTdE
),()(
.
Сравнивая, получаем энергии равновесного ЭМ
излучения:
1
3
32
),(
x
ec
T
-
формула Планка. Была получена из соображений что
вещество стенок поглощает и излучает свет порциями
величиной
. Отсюда следует, что уровни
энергии атомов дискретны.
21. Законы равновесного ЭМ излучения. Излучение
АЧТ. Уравнение состояния фотонного газа. Функция
Стефана-Больцмана для интегральной плотности
энергии. Формула Бозе-Эйнштейна:
1
/
2
332
)(
kT
e
d
c
V
dn
,
1
/
3
32
),(
kT
ec
T
.
)()(
dndE
в интервале от
до
+d
и
VdTdE ),()(
в
интервале от
до
+d
. Далее
)()(
dEdE
,
.
0
)(),( TdT
,
0
1
/
3
32
)(
kT
e
d
c
T
.
kT
x
,
x
kT
,
dx
kT
d
.
0
1
3
32
)(
x
e
dx
kT
x
kT
c
T
15
4
0
1
3
4
32
x
e
dxxkT
c
. Следовательно
4*
)( TT
, где
33
42
4
4
32
4
*
1515
c
kk
c
. Закон смещения Вина. (График
),( T
от
, такой горбик, его вершинка есть
0
). Как будет меняться
0
при изменении T? Вершина есть
0
.
)
1
/
1
3
(
kT
e
0
2
)1
...
(
...
)1(
3
1
/
1
2
3
kT
e
e
kT
e
.
Т.е.
1
...
...
3
e
e
kT
. Пусть
kT
x
0
0
. Предположим что x
0
нашли. Тогда
0
0
kTx
,
T~
0
(З-н Вина) с
повышением Т max смещается вправо, площадь под кривой
сох-ся => горб стан-ся ниже, шире. и
T
1
~
0
1
~
0
. Закон смещение – т.к.
максимум смещается вдоль оси частот. Закон Вина и
Релея-Джинса.
1
kT
,
kT
,
1
/
kT
e
,
kT
e
c
T
/3
32
),(
(з-н Вина). Если
1
kT
, то
kT
. Следовательно
kT
kT
e /1
/
. Далее,
2
32
/
3
32
),(
c
kT
kT
c
T
.(релея-джинса) Большое историческое значение. Ф-лы
были получены до ф-лы Планка. Ф-ла Пл универсальна она
раб-т на всех частотах. Ф-ла Вина раб-т на больших
частотах, ф-ла Р-Д на малых частотах.
Равновесное ЭМ и АЧТ. АЧТ: стенки полости чернятся .
после 2-3 взаим-й со стенками излучение полностью
поглощается. Любое изл-е падающее на отверстие
поглощается полностью и из полости уже не выходит, п/э
если из полости исходит какое то излучение то это
собственное излучение, не отраженное, т е отвестие ведет
себя как абсол черное тело.
Легко показать что если отверстие маленькое, а полость
большая, то состав излучения будет такой же как для
равновесного излучения. Из полости идет поток лучей. За 1
сек б получено эн: dU=Scdt Ф-ла показ-т что светимость
б с
4
c
L
(*)1 з-н Кирхгофа (светимость -
испускательная способность черного тела. Т е излучение эн
в ед времени на ед площади) справа плотнось эн
равновесного э/м излучения. Ф-ла показ-т что L=> все з-
ны рассмотренные ранее:з-н П, Больц, Вина,и др
автоматически переносятся на изучение тв тела. Но сущ-т
коррекция: если =T
4
, то L=c T
4
/4=* T
4
, где *=
2
к
4
/60
с
2
h
3
З-н Вина для частоты
m
переносится без всякой коррекции
на черное тело. З-н Кирхгофа записан для интегральной
плотности, но верно он б справедлив для спектральной
плотности.
d
Tc
dL
4
),(
(спектра
льная плотность)
Второй з-н Кирхгофа: отношение испускательной
способности тела к его поглощательной способности =
испускательной способности тела. Испускательная спос-
ть(I
и
) - это то же что и светимость(L).
А-отражательная способность
В- поглащательная способность
I
пад
- интенс-ть падающего излуч-я (по всем направлениям в
ед времени на ед площади)
А=Iотр/Iпад
В=Iпогл/Iпад А+В=1
Iпогл+Iотр=Iпад
2 з-н гласит что Iисп/В=L (это в сущности один из законов
т/д)
имеется полость, одна часть стенки черная, а др серая, но в
полости равновесное излучение.1) на любой участок
стенки в ед времени падает одно и то же кол-во эн. 2)
чтобы стенка не остывала и не нагревалась она д испускать
столько эн , ск поглащать. (Iисп=Iпогл). Для черного тела
А=0 Iотр=0 (черное тело не отр-т) L=Iпогл=Iпад
возьмем серый уч-к В=Iпогл/Iпад=Iисп/L
L=Iисп/В
Термическое уравнение состояния равновесного
излучения. Для любой простой системы:
p
V
T
p
T
T
V
U
. ЭМ
излучение в полости – фотонный газ, простая система. =>
знаем калорическое ур-е состояния.
),( TVUU
,
VU
,
4*
T
, =>
4*
VTU
-
калорич. ур-е состояния. Термическое ур-е:
p
V
T
p
TT
4*
,
T
p
T
T
p
V
T
p
T
T
2
1
2*
.
)/(
2
TpddTT
)(
3*
3
1
VA
T
p
T
=>
TVATp )(
4*
3
1
.
С эксперим. данными согласуется только
0)( VA
(опираясь на 3 начало т/д),
3
4*
3
1
Tp
,
UVpV
3
1
3
1
.давление
фотонного газа оказалось независящим от объема и равным
1/2 плотности эн.
2.Вычисл.давл-ия на стенку сосуда. Рассм-им упр-ое
соуд-ниемол-лы со стенкой. При столк-ии нормал-ая
проекция мен-ет знак, а касат-ая ост-ся. Если ось перпенд-
на стенке, то:
y
V
y
V
x
V
x
V
z
V
z
V
12
;
12
;
12
. Где V1 и V2 – скор-ть ч-цы до и после удара. Изм-ние
имп-са ч-цы:
k
z
mVp
2
2
, где к-
един-ый вектор по оси oz. При кажд. соуд-ии стенка получ-
ет равное по мод-лю, но против-ое по напр-ию приращ-ие
имп-са. Пусть
П
-импульс получ. стенкой площ-ю
S за время
.t
Тогда имеем
tFП
,где
F
- средн.сила давл-ия
со стор-ны молекул на стенку. По опред-ю F/S –есть давл-
ие. Осн-ая труд-ть расчета давл-ия закл-ся в том, что мол-
лы имеют разные скор-ти. Но если бы увсех мол-ул была
одна и та же проекц. скор-ти Vz, за время
t
все ч-цы
в слое толщ-ой
t
z
V
дошли бы до стенки. Их ср-
ее число
tSnz
V
, n – плот-ть газа.
t
возьмем наст-ко малым, что
t
z
V
будет меньше
длины своб-го пробега, тогда столк-ем между собой
молекул можно прен-чь. На самом деле только часть мол-
ул имеет зад-ое знач-ие Vz. Таких ч-ц в ед-це объема по
распр-ию Максв.:
z
dV
z
V
en
z
VndW
z
Vdn
2
2/1
)()()(
. Отсюда ср-нее число ч-ц, имевш-их скор-ть Vz и удар-ся
о стенку за время
t
:
z
tdVS
z
V
z
V
entS
z
V
z
Vdn
2
2/1
)()(
.Част-цы перед-ут стенке имп-льс равный
tS
z
dV
z
V
z
V
enm
2
2
2/1
)(2
. Проинтегр. Это выраж-ие по Vz, в пред-ах от 0 до беск-ти
и разделив рез-тат на
tS
, получ-им:
0
2
22/1
)(2
z
dV
z
V
e
z
VmnP
. Спом-ью ф-лы в прилож-ии наход-им давл-ие газа на
стенку сосуда:
V
mNmn
P
22
,Сравн-
ая это соотн-ние с ур-нием Менд.-Клап-на:
kNTRT
m
PV
, устан-
ваем,что
kT
m
2
.С пом-ью этой ф-лы уст-ся
физ-кий смысл парам-ра
, вход-го в закон арспр-ния
мол-ул по скор-тям, а также выявл-ся статистич. хар-тер
темп-ры.Темп-ра есть особая мера инт-ти внутр-го движ-
ия:от темп-ры зависит,какая часть всех мол-ул имеет те или
иные скор-ти,а след-но,и энергии.
5. Определение энтропии и ее свойства. Закон
возрастания энтропии в замкнутой системе. Если знаем
ФСР ,т.е. распред. вер-й, то можем найти L
макро
=L
ср
=
i
i
W
i
L
ФСР определяет М-сост-е системы
i
WkS ln
-энтропия (k-пост.
Больцмана,знач-е имеет “-”,т.к. сост-е равновесия соот-т
максимуму системы)
i
W
i
WkS ln
. рассмотрим
св-ва этой вел-ны:
),,(
1
nE
i
W
- для равновесного сост-я
1
1
ln
1
i
i
kS
S=kln-
формула Больцмана для равновесного сост-я. 1)сост-е
равновесия энтропии опред-ся числом микро-сост. его
реализующих 2)вел-на аддитивна, если система состоит из
2 квазинезавис-х подсистем, тогда Е=Е
1
+Е
2
и как следствие
S=S
1
+S
2
покажем это, т.к. системы в 1-ом приближении
независимы, то вер-ть того, в каком сост-и находится 1-ая
часть никак не связана с вер-тью того в каком сост-и
находится 2-ая часть. Спектр состоян. также независим.
)1(
i
W
,
)2(
k
W
- введем ФСР для
каждой части также и S
1
=-k
i
W
i
(1)
lnW
i
(1)
и S
2
=-
k
k
W
k
(2)
lnW
k
(2)
сост-е системы можно хар-ть 2 индексами i -
1-ая часть и k -2-ая часть. Можно ввести вер-ть для всей
системы
ik
W
и энтропию всей системы S=-k
i
k
W
ik
lnW
ik
- в силу независимости подсистем W
i k
=W
i
(1)
W
k
(2)
,
условие нормировки вер-ти
i
Wi
(1)
=1 и
k
W
k
(2)
=1
i k
k
W
i
W
k
W
i
WkS
)2()1(
ln
)2()1(
…=
i
i
W
k
k
W
k
W
k
k
W
i
i
W
i
Wk
)1()2(
ln
)2()2()1(
ln
)1(
. S=S1+S2 энтропия системы равна сумме энтропий
подсистемы. 3) введенная функция энтропия в сост.
равновес. имеет максимум
i
i
W
i
WkS ln
, W
i
=1.
Дадим всем вер-ям малые приращения и потребуем, чтобы
при этом изменение энтропии = 0.
i
i
W
i
dWkdS )1(ln
. Какие бы ни были вер-ти старые или новые они должны
удовл-ть условию нормировки, => их приращение не
является полностью независимыми. Продиф-м условие
нормировки, получим
0
i
i
dW
.
i
W
i
dWkdS ln
.
Экстремуму соот-т случай когда dS=0 или
0ln
i
W
i
dW
(2) => что если все
W
i
независимы, то 0 получим когда все lnW
i
=0. Найдем
такие вер-ти, чтобы
0ln
i
W
i
dW
(*) и
0
i
dW
(3). Умножим рав-во(3) на а
и сложим с(*) (это метод Лагранжа).
0)(ln
a
i
W
i
dW
что
позволяет какое-то одно Wi выразить через все
остальные. Значит одно зависит от всех, а все остальные
независимые. Подберем a
1
так чтобы
1
ln
1
Wa
. =>
0)(ln a
i
W
i
dW
при
i1. но в этой сумме все приращ-я можно считать
независимыми, => рав-во суммы =0 тогда, когда все
скобки=0,т.е. при выполнении lnW
i
+a=0. Но это рав-во
выполняется и для 1-ого сост-я, => для всех i выполняется
lnWi=-a => экстремум может быть в точке ,где вер-ти всех
сост-й одинаковы. Этому признаку удовл-т равновесные
сост-я. Постулат: энтропия изолир-й системы не убывает
достигая максимума в сост-я равновесия.
0
dt
dS
или
0dS
, причем рав-во соот-т равновесному
сост-ю. В равновесии все микросост-я равновероятны. При
заданных условиях все м-сост-я имеют шанс реализоваться
и ни одно не появляется чаще других. Так может быть
если движ-е частиц беспорядочно, т.к. любая
согласованность в движ-ии уменьшает число сост-й,
которые могут реализоваться или выделяет особые сост-я.
Хаотизация-полное забвение начальных условий, в
которых система родилась. Закон возрастания энтропии
определяет физич-й смысл введенной вел-ны: -опред-т
наличие равновесий в системе или степень близости
системы к равновесию => м. рассчитать полученное тепло.
МКР и закон роста энтропии явл-ся исходными. Они не
выводятся, а постулируются.
7. Равновесный процесс. Статистическое определ. T,
хим.потенц, p. Основное ТД р-во-н-во. Статфизика и
ТД. Равн. сист (Рсис) – самые простые. Если знаем в ней E,
N, , то можем опр. ее микросостояние
),,(
NE
, а значит можем опр. и
энтропию. Можно вычислить и другие макроскопич. х-ки.
Рассм. мн-во равновесных состоян. На нем можем
математич. задать переходы из одного макрсост в другое,
не заботясь о их реальности. Такие переходы называются
равновесными процессами. Мы можем осущ. реальные
процессы, близкие к равновесным. Изменение энтропии в
равновесн. процессе происх. в рез-те изменения параметров
S=S(E,N,).
),,(ln
NEkS
,
d
S
dN
N
S
dE
E
S
S
. Придумаем упрощающ. обозначения:
TE
S 1
,
T
S
,
N
S
T
. Подставим в
S
и
умножим на T. =>
ddNTdSdE
. По
форме это совпад. с основным ТД рав-вом. Слагаемые: 1 –
измен. E при пост N и , в ТД это – теплота. 2 – Измен. E
связан. с перемещ. частиц, 3 – измен. E связанное с измен.
внешних параметров – работа. Т.е.
A
N
dEQdE
- пришли к 1
началу ТД. Это т.к. Рсис – целиком определ. E, N, . ТД
понимает это шире – считает его справедливым и для
неРсис и процессов. Мы к этому прийти не может. Но мы
получили 1 начало из статист. теории независимо от ТД. II
начало. Рассмотрим когда и N=const.
T
dE
dS
. dE – получена в форме тепла.
Введем
TdSdQ
,
T
Q
dS
.
Q
- энергия, которую сист. получает или отдает
извне в Рпроц. В неРпроц:
SdSddS
. Первая часть – в рез-те
получ. тепла
T
Q
Sd
,
Sd
- в рез-
те внутр. причин. Оно имело бы место даже когда внешние
влияние отсутствовали. Для изолир. системы
0
Sd
, поэтому полное
T
Q
dS
. Это и есть ф-ка II начала. Т.е. получили независимо от
ТД. 1 аксиома. Система сама собой приходит в Рсост и
никогда из него не выходит. Это т.к.
0dS
.
Равенство – именно для Рсост. Система не может выйти из
Рсост, т.к. ее S уменьшилась бы сама собой. Постулат о T.
Теплообмен не надо вводить постулативно т.к. в основе
статфизики что все сост. из частиц и он появл. естественно.
Температура здесь – величина, характ. возможность и
направление передачи энергии.
E
S
T
1
.
Возьмем систему, разделим на 2 части.
21
SSS
. =>
21
dSdSdS
=>
2
2
2
1
1
1
dE
E
S
dE
E
S
2
2
1
1
1
1
dE
T
dE
T
и т.к.
21
dEdE
. =>
0)
2
1
1
1
(
1
TT
dEdS
. Т.е.
21
0
1
TTиdE
и наоборот. Если
T
1
=T
2
, то dS=0 – равновесие, теплообм. нет. В ТД есть
постулат об ур-ях состояния. Это есть следствие того, что
),,(
NESS
(Рсист). От E, N,
можно всегда перейти к T,N, т.к. T определена через S.
Тогда S=S(T,N,). Через пр-ные от S можно определить и
все другие величины, где обобщенная сила и
химпотенциал были найдены. 3 начало. Оно получается
простым следствием квантовых закономерностей
),,(ln
NEkS
(Рсист). Для
всех систем T убывает вместе с E, если зафиксировать N и
. Поэтому охлаждение системы есть отнятие E у нее. E
можно отнимать пока система не придет в основное
энергетич. состояние:
)
0
(ln)0( EkS
, где E
0
–
основной нижний энергетич. уровень. Для б-ва систем он
не вырожден. Если =1, то S=0. Если 1, то кратность
вырождения осн. состояния невелика. Тогда S будет близка
к нулю т.к. мал ln, k мала. Поэтому практически S0 при
T0. Но ТД не есть глава из стат.теории, т.к. ТД может
быть сформулир. как отдельная наука и во всех случаях,
когда важна только феноменологическая сторона
процессов и явлений, рассмотрение их в рамках статистики
приведет только к излишней сложности. Добавочка: для
вычисления макроскопич. величин достаточно знать
распредел. вероятн. для появления отдельных
микросостояний. При этом реальное движение в системе
заменяется изучением этого распределения вероятностей.
dqdppqfpqLL ),(),(
.
8. Вывод формулы канонического распределения.
Имеется большая сист. В следствие изолир-ти Е=const,
N=const, T=const. Она равновесна, значит к ней м.б.
применено МКР. Все микросост-я нашей сист.
равновероятны. Допустим, что сист. состоит из 2 частей. У
малой части энергия , у другой – Е-. В малой части
n=const, в др. N-n=const. Внеш. параметры
1
=const и
2
=const. Если сист. равновесна, то каждая ее часть
равновесна. Поставим цель, что наша часть обладает
энергией . Если комплекс изолирован, то малая часть и
оставшаяся часть (термостат) нах-ся во взаимод-ии,
поэтому энергия обеих частей может изменяться.
Закономерен вопрос: какова вер-ть того, что малая часть
обладает энергией ? Допустим, что малая сист. и
термостат квазинезависимы. W()-? , E-.
случаиыевсевозможн
случайныйблагополуч
W
;
),(
)(
E
W
;
E,
- число сост-ий большой сист.,
для которых указывается разделение по энергиям. -
всевозможные сост-я большой сист. эта формула
справедлива, если все сост-я комплекса равновероятны. В
условиях равновесия данное условие выполняется
автоматически.
E
T
E
*
,
,
*
-число сост-ий малой подсист. С энергией
.
E
T
- число сост-ий термостата с
энергией Е-. В силу квазинезависимости того и др.
объекта
E
T
*
;
E
T
E
T
W
*
*
. Допустим, что <<Е.
E
T
можно
разложить в ряд. Для любого равновесного объекта
справедлива формула
T
kS ln
T
k
T
S ln
;
E
T
kE
T
S ln
;
E
T
S
k
E
T
1
exp
. Энтропию разложим в ряд.
...
E
S
E
T
SE
T
S
;
E
S
k
E
T
S
k
E
T
11
exp
;
E
T
S
k
E
T
S
k
E
T
S
k
E
T
S
k
W
11
exp
*
11
exp
*
;
E
T
S
k
1
exp
от не зависит, ее
можно вынести за знак суммы.
E
T
S
k
E
T
S
k
W
1
exp
*
1
exp
*
. По опред-ю
TE
S 1
;
kT
kT
W
exp
*
exp
*
. От термостата осталась только темп-ра Т. Однако в
условиях равновесия темп-ра термостата есть также и
темп-ра и малой подсист. и всей большой сист. Т.о. от
термостата ничего не осталось. Он задает пост-ую темп-ру
для нашей малой подсист. можно убрать *, т.к. фигурирует
лишь число сост-ий нашей подсист.
kT
kT
W
exp
exp
. Это соотношение называется каноническим
распределением Гиббса.

9. Особенности и св-ва канонического распределения.
Вычисление ТД величин с помощью КР. Имеем
каноническое распределение в виде приближенной
формулы:
)1(
)exp(
)exp(
i
kT
kT
i
W
.Канонич
распределение отвечает на вопрос- каково вероятность
того, что малая подсистема являющаяся частью большого
равновесного объекта находиться в i-ом квантовом
состоянии. Характерное свойство этого распределения
)exp(~
kT
i
i
W
. Все состояния с одной
и той же энергией явл-ся равновероятными. Вероятность
тем больше чем ниже ε системы . В знаменателе
распределения стоит
i
kT
i
z )exp(
-статис сумма или
сумма по состоянию. В самом распределении сумма играет
нормировочный множитель, однако дальше мы выясним,
что через не находятся все термодин характеристики. В
формуле распределения фигурирует так же температура.
Это единственное чем проявляет себя термостат.
Температура считается фиксиррованной заданной. А
энергия переменная ввеличина, которая может хаотически
меняться. Интересен вопрос о вероятности тех или иных
значений энергии W(ε)-? Ответ элементарен. Надо
использовать теорему о сложении вероятностей. Взять
сумму вероятностей для всех состояний, в которых энергия
принимает значения ε. Предположим, что таких состояний
Ώ(ε) – статис вес энергетического состояния или кратность
вырождения энергетического состояния. Так как состояния
с одной и той же энергией равновероятны:
)()()(
i
WiW
z
kT
W
)exp()(
)(
,но с
другой стороны
)exp()()exp(
kT
i
kT
i
z
отсюда следует
)2(
)exp()(
)exp()(
)(
kT
kT
W
.
Написанное соотношение отвечает на следующий вопрос-
какова вероятность того, что малая подсистема входящая в
состав большого равновесного комплекса будет обладать
энергией ε. Это соотношение так же называется
каноническим распределением. То есть каноническое
распределение представлено в двух формах. Однако (1)
используется чаще чем (2). Обе формы распределения
являются нормированными. Посмотрим на распределение
для энергии
)exp()(~)(
kT
W
-
Ώ(ε) – быстро растет с ростом энергии, а
)exp(
kT
- очень быстро убывает. При
малых энергиях существенен первый сомножитель, при
больших второй. Поэтому график распределения имеет
характерную колокобразную форму с максимумом в точке
ε
н
– наиболее вероятная энергия. Для макро объектов этот
мах очень острый. Поэтому существ значение имеет только
небольшой отрезок ε, лежащий около ε
н.в
. острота пика
приводит к тому, что выполняются некоторые
приближенные соотношения. Среднее значение энергии
нв
. Термодинамические характеристики
находятся как средние по распределению
макро
LL
)(
LL
. Это часто
облегчает расчет. Вычичсление термод величин с помощью
канонич распределения:
L
макро
L
или
i
i
kT
i
i
kT
i
i
L
i
W
i
L
макро
L
)exp(
)exp(
Если
i
L
значение микроскоп аналога в i квантовом
состоянии . И в числителе и в знаменателе суммы берутся
по всем возможным квантовым состояниям системы.
Несколько другие будут формулы
)(
i
L
i
L
. В этом случае удобнее пользоваться распределением по
энергиям, а не по состояниям.
z
kT
LWL
)exp()(
)()()(
)exp()(
)exp()()(
kT
kT
L
Это общие соотношения. Чтобы сделать расчеты надо
знать все возможные уровни энергии и кратность их
вырождения.
)exp()(
)exp()(
kT
kT
U
)exp()(
kT
TT
z
)exp()(
kT
)exp()(
2
1
2
1
kT
kTT
k
тогда окончательно для энергии
z
T
z
kT
U
2
z
T
kTU ln
2
Если использовать
эти приближенные соотношения то можно получить
несколько простых формул:
STuF
T
F
T
U
илиSFU
T
S )(
1
.
В результате все термодин величины могут быть
выражены через статис суммы и ее производные. Однако
остается проблема вычисления самой z. Есть разные
способы. Но наиболее часто исполь-ся полукласс
приближенное вычисление.
10. Приближенное выражение для статистической
суммы. Приближенное выражение для числа квантовых
состояний. Классическое каноническое распределение.
)exp(*)(
kT
Z
Уровни энергии ε обычно расположены очень густо,
поэтому на млом интервале dε на котором экспонента
остается практически постоянна, расположено еще очень
много уровней. Это позволяет перейти от суммирования по
уровням энергии к суммированию по интегралу энергии
i
kT
d
kT
Z )exp(*)()exp()(
-число состояний на интервале . d()- число
квантовых состот. В инт-ле ,+d. Для нахождения d()
используется приближенная формула
3
)2(
)(
)(
dГ
d
, где dГ() -
классический фазовый объем приход-ся на все
микросостояния в интервале энергий dε. В частности для N
–частиц идеального газа мы можем использовать соотн-е
N
N
dГ
d
3
)2(!
)(
)(
. В
этой формуле учтено, что в ид газе 3N степеней свободы и
учтена тождественность частиц. В рез-те для ид газа
получаем
)exp(*)(*
3
)2(!
1
kT
dГ
N
N
Z
. Для классической сист
),( pq
- ф-я
коорд-т и имп-са Можно подобрать такие малые инт-лы
q,q+dq и p,p+dp изм-ния коорд-ты и имп-са для которых
энергия сист-мы попадает в интервал ,+d. В этом случае
эл-нт объема dГ()=dq*dp, можно отождествить с
произведением dq*dp и тогда в данном инт-ле от интегрир-
я по энергии перейдем к инт-лу по q и p.
)
),(
exp(***
3
)2(!
1
kT
pq
dpdq
N
N
Z
в таком виде чаще и используется стат сумма. Данное
приближение для стат суммы называют
квазиклассическим. приближенная оценка числа
состояний: в тех случ когда движение близко к класич
можно попытаться действовать так:
pq
мы можем выделить некот
объем фазового пространства приход-ся на все его
состояния
-число состоян которое
может иметь система при тех условиях при котор нах-ся
фазовый объем
)2(
где -
число степеней свободы. I-ой степени свободы мы можем
сопоставить q
i
и p
i
. для квантового состояния обе перемен
могут быть указаны в пределах неточностей, которые
задает нерав-во Гейзенберга.
2
i
p
i
q
Если для всех степеней
свободы мы запишем такие нерев-ва, а затем перем-м то
получим такое соотношение
)2(
i
p
i
q
i
П
)2(
)2(
прямое использование этой
формулы в ряде случаев заведомо приводит к неверным
рез-м. Действительно, данная формула учитывает только те
особенности квант состояний которые связаны с
движением частиц в пространстве. Однако квант состояние
могут различаться по параметрам которые не связаны с
движ в пространстве(напр в связи со спином ). В отличие
от классики в квантовой теории имеет место
неодинаковость, а полная тожественность частиц.
Перестановка двух частиц местами в классике приводит к
новому сост сист в квантовой теории перестановка местами
частиц не дает нового состояния, но тождеств чстиц учесть
очень просто. Если система состоит из N невзаимод-х
частиц то все тождественные состояния можно получить
путем перестановок частиц. Поэтому реальное число
состояний будет в N! раз меньше.
)2(! N
В системах
одинаковых фермионов дей-т запрет Паули, состоящий в
том, что в одном квантовом состоянии не может быть
более одной частицы. классическое каноническое
распределение Квант канонич распределение
)exp()(
)exp()(
)(
kT
kT
W
допустим, что сист близка к классич и дискретную W
можно заменить непрер
d
dW
W
,
)(
)(
вопрос вероятн-ти
нахождения в интервале ε, ε+dε. ε, ε+Δε- малый но
конечный интервал.
)exp()(
)exp()(
)(
kT
kT
W
интервал Δε- выбирается так, чтоб он был мал настолько,
что экспоненту в его пределах можно считать постоянной,
с др стороны на нем должно быть много уровней ()
Δε0
)exp()(
)exp()(
)(
kT
d
kT
d
W
,
)2(
)(
)(
dГ
d
)1(
)exp()(
)exp()(
)(
kT
dГ
kT
dГ
W
Записанное в формуле (1) классич канонич распредел-е
отвечает на вопрос какова вероятность того, что энергия
окажется в интервале ε,ε+dε, однако согласно теории
вероятности в этом случае dW()=f()*d данная формула
записана так, что f(x)- плотность вероятности. Из нее
можно извлечь
)2(
)exp(
)exp(
)exp()(
)exp()(
)(
d
Г
kT
Г
kT
kT
Г
kT
Г
W
Г
kT
f )exp(~)(
-
явный вид уравнения распределения. Стоящий в
знаменателе интеграл играет роль нормиров-х множителей.
При использовании (2) находим
Г
, Г()- фазовый
объем приход-ся на все микросост системы если ее энергия
изменяется в пределах от 0 до ε и наконец можно
вспомнить что для класс сист ε=ε(q,p)- энергия -функция
обобщ координат и импульсов
dqdpdГd
dppp
dqqq
)(,
,
,
)3(
)
),(
exp(
)
),(
exp(
),(
kT
pq
dqdp
kT
pq
dqdp
pqdW
Ясно что мы получили справа распр-е вер-ей для коорд и
имп. Данная формула отвеч-т на вопрос какова вероят-ть
того, что коорд и импульсы одновремен попадут в задан-й
интерв dq и dp поскольку через коорд и импульсы в
классике задается микросост сист, то эта же форм-ла может
отвечать на вопрос какова вер-ть реализаци того или иного
микросост сист, т.е в данном случае ф-ия
)
),(
exp(
)
),(
exp(
),(
kT
pq
dqdp
kT
pq
pqg
есть плот-ть вероят-ти для микросост или ф-ии статист
распред для изотерм классич-й сист Пусть М-точка
фазового прост-ва
)4(
)
),(
exp(
)
),(
exp(
)(
kT
pq
dГ
kT
pq
dГ
MdW
Классич канонич распред-е использ-ся для расчета
макроскоп-х парам-ов
dqdp
kT
pq
dqdp
kT
pq
pqL
pqdWpqLL
макро
L
)
),(
exp(
)
),(
exp(),(
),(),(
- аналогично квантов случ-ю вместо сумм стоят инт-лы.
Z
стат
I-статич инт-л.
d
kT
Г
kT
dГ
kT
pq
dqdpI )exp()exp()()
),(
exp(
. Если в квант расчетах фундам роль играет статис-я сумма
Z, то в классич-х расчетах аналог-ю роль должен играть
статис-й интеграл –I. Можно показать, что расчет т./д
велич-н можно свести к вычисл-ю интеграла I и его произв-
х. Причем соотв-е формулы повтор-ют квант-е
соотношения
)*ln(
2
*ln
2
* aI
Z
TkUZ
Z
TkU
)*ln(ln aIk
T
U
SZk
T
U
S
)*ln(ln aIkFZkF
. Класич-е формулы имеют одну неприятн-ю особеность
дело в том, что статис интеграл I явл-ся размерной велич-й.
Вводят в формулы дополнит-й множит-ль (произ-й). В
кач-ве расплаты класич-я т./д функ-ии оказывается
определенными с точностью до постоян-го слагаемого
очень часто поступ-ют по другому: статич интеграл I в
класич формулах замен-ют приближ-ми квазиклас
выраженим для статис суммы
dqdp
kT
pq
N
N
I
)
),(
exp(
3
)2(!
1
11. Расчет статистической суммы для классического
одноатомного идеального газа. Нахождение ТД ф-ций и
ТД ур-я состояния системы. всякое исследов теории
начинают с модели сист. При этом модель может
приближенно или точно отражать все качества реального
объекта. Простейшей системой явл ид газ. Каждую частицу
мы можем моделировать матем точкой т.к газ
одноатомный. Газ заперт в некотором объеме назначение
стенок не выпускать частицы наружу, а чтобы стенки не
мешали расчету, чтобы не учитывать краевые условия
будем считать что столкновения упругие. На первый раз
полагаем, что никаких других внеш полей нет. По
определению газ называют идеальным если нет взаимод
м.у частицами. На самом деле мы просто считаем, что
взаимод-е прходило мало, если бы вообще не было
взаимодействий, то каждая частица двигалась сама по себе
и присут-ие других молекул для нее было бы не заметно.
Следствие: энергия сист равна сумме энергий всех частиц.
1i
i
E
Будем предполагать что частицы
дв-ся по законам класс мех-ки.
iz
p
y
p
x
p
m
i
V
m
i
)
222
(
2
1
2
2
Предположим что газ равновесен и с пом-ю термостата Т-
постоянна. Найдем энергию газа как функцию (T,V,N)
тогда р=Р(Т,V,N). Зная Е и р рассчитаем остальное.
Применим каноническое распределение и все вытекающие
формулы. Расчет ТД хар-к начинается с вычисления стат
суммы. Стат сумма будет вычисляться в
квазиклассическом виде т.к. система практически
классическая.
dqdp
kT
pq
N
N
z )
),(
exp(
3
)2(!
1
Множитель добавить легко; в классической физике всё
равно интеграл надо множить на какую то константу чтобы
получить безразмерную величину под логарифмом;
квантовая Т подсказывает какая должна быть конст; без
этого множителя не получиться правильной зависимости
энерг от числа частиц. Рассмотрим инт-л.
i
qNi ,..2,1
i
p
z
p
y
p
x
p ),,(
iz
dp
y
dp
x
dxdydzdp
N
i
П
i
N
i
z
p
y
p
x
p
kT
N
N
z )(
1
)
1
222
2
1
exp(
3
)2(!
1
В качестве обощенных коэфф выделим x, y, z. Интегрир
по коорд отделяется от интегр по импульсу. Пределы
изменения переменных огранич стенками сосуда.
izyx
N
i
i
N
i
zyx
N
i
N
dpdpdpПppp
mkT
x
dxdydzП
N
z
)(*))(
2
1
exp(
*)(
)2(!
1
1
1
222
1
3
Коэффициенты каждой частицы не связаны с коэфф других
частиц.
V V
N
i
dzdydxdzdydxdxdydzП
222111
1
dVdxdydz
VdV
N
i
N
i
VdxdydzП )(
1
Легко
сообразить что инт-л по имп разбивается на ряд
множителей однотипных по структуре т.к. exp можно
разбить произведением exp.
)exp(*)exp()exp(
)
2
2
exp( dp
mkT
-для каждой
частицы. Имеется сложность вычисления отдельного инт-
ла т.к. энергия всего газа постоянна, она складывается из
имп отд частиц, имп зависят др. от др.
N
i
iz
dp
y
dp
x
dp
m
constE
1
)
222
(
2
1
Но мы можем взять пределы от - до .
dp
mkT
p
)
2
2
exp(
m
p
2
2
-
энергия на одну степень свободы может быть=0 и равна
всей энерг газа(
E
m
p
2
2
0
NkTE
2
3
N
mkT
p
NkT
m
p
2
3
2
2
max
2
3
2
2
max
2
)
2
exp(
dzz
mkT
mkT
p
mkT
2)
2
2
exp(
2
1
2
3
)2(
3
)2(!
1
N
mkT
N
V
N
N
z
Нахождение ТД хар-к идеал газа.
2
3
)2(
3
)2(!
1
N
mkT
N
V
N
N
z
Стат сумма предст собой функцию z= z(T,V,N)
z
T
kTU ln
2
zkTF ln
zk
T
U
S ln
)2ln(3!ln)2ln(
2
3
lnln
NNmkTNVNz
Т.к. N>>1 тогда применим ф-лу Стирлинга
xxxx ln!ln
. Все последующие
члены мы отбросим.
)(!
e
x
x
NNNNmkT
N
VNz ln)2ln(3)2ln(
2
3
lnln
T
N
mkT
mkT
N
mkT
N
T
z
T 2
3
2
2
1
2
3
))2ln(
2
3
(ln
тогда найдем вид U,S,F:
kTNkT
T
N
kTU
2
3
2
3
2
3
2
2
3
)
4
2
(ln
)2(
2
3
)2(
ln
)1ln)2ln(
2
3
)2ln((ln
223
3
mkT
N
Ve
kTN
N
mkTVe
kTN
NmkTVkTNF
2
3
)
2
2
(ln
2
3
mkT
N
eV
kNNk
T
F
T
U
SSTUF
Посмотрим что будет с S, если Т0 тогда S= -, это
противоречит 3 началу ТД (S должна стремиться к 0) это
связано с тем, что мы пользовались класс физикой, а при
низких тем-х она неприменима.
2
3
)
2
(
2
5
ln)
2
3
)
2
(ln
2
3
(
22
mkT
N
Ve
kN
mkT
N
eV
NkS
. Найдём р
NV
V
p
p
,
)(
2
3
)
2
(ln(
2
mkT
N
eV
kTN
V
p
V
kTNmkT
N
e
mkT
N
eV
kTNp
2
3
)
2
(
2
3
)
2
(
1
2
2
В этой области и другие выражения явл неверными.
Совпадение выведенного термического ур-я с
эмпирическим ур-ем Менд-Клапей явл подтверждением
стат теории, с др. стороны сделанный вывод предст собой
теор обоснование ТД формулы ур-я сост идеал газа.
13. Реальные газы. Модель слабонеидеального газа.
Вычисление конфигурационного интеграла. Модель: 1)
молекулы - твердые непроницаемые шарики, массой m,
радиусом r. 2)будем считать, что движение происходит по
законам класс механ. 3) газ сосредоточен в пределах некот
объема. 4) между молек имеется взаимод, котор до сих пор
неизвестно в деталях, но глав черты узнаем введя ряд
допущений.
U
N
i
mV
E
1
2
2
),..2,1( NrrrUU
Если
подставим эту энергию в фор-ы статфизики мы не будем
знать что с ней делать, поэтому введём ряд положений:
взаимод всех молек можно свести к попарным взаимод
всех молек, каждой молек со всеми другими.
ki
k
r
i
rUNrrrU
,
),(),..2,1(
Сумма берется по всем парам частиц. Будем предполагать
далее, что энергия попарного взаимод 2х частиц зависит
только от расстояния между ними. Для дальнейшего
полезно знать сколько можно составить пар, это число
выборок по 2 частицы из N возможных. Из математики
2
)1(
)!2(!2
!
2
NN
N
N
N
C
. Учитывая, что N>>1 мы можем считать число пар N
2
/2.
Конечно зависимость энергии взаимодействия от
расстояния между частиц явл универсальной в том смысле,
что для каждой пары она одна и таже. Поэтому мы можем
рассмотреть функц W(r)- зависимость потенциальной
энергии взаимодейст 2х част от расст между ними.
dr
dW
F
- сила взаимод. При r<r
0
dW/dr<0
поэтому F>0- отталкивание, в обратном случае притяжен.
F(r
0
)=0 – тч. равновесия (график: ось x-r, y-W, график-
кулоновское отталкивание). Нарисованный график
нехорош в отношении: на самом деле левая
отталкивательная ветвь очень круто идёт вверх, поэтому
для многих целей использ упрощ модель, а именно,
считают. Что в точке r
0
расположена как бы стенка ближе
которой частица подойти не может.
0)0(
~
;)0(
~
rrWrrW
Легко сообразить. Что 2 молек рассмотренные как твёрдые
непроницаемые шарики не могут сблизиться на расстоян
меньше d, поэтому с большой точностью предположим
r
0
d. В большинстве для электронейтральных атомов и
молекул силы взаимодействия быстро убывают с расстоян.
Обычно считается. Что они убывают r
6
)0(,
5
1
~)( rr
r
rW
поэтому на расст порядка 3-4r
0
W(r)0. Очевидно, что
наибольшее значение в тч r
0
. Вытекает основное
допущение: будем считать
1
)0(
~
kT
rW
. Физич смысл этого
нерав-ва: величина кТ порядка средней кинет энерг дв-я
частиц. Поэтому это означает, что потенциальная энергия
взаимодейст 2х частиц << Е
к
. Стат сумма для газа,
конфигурационный инт-л. Мы будем исп-ть квазиклассич
выр-е для стат суммы
dqdp
kT
pqE
N
N
z )
),(
exp(
3
)2(!
1
(*). Договоримся в кач-ве коорд мы выберем обычные
декарт x
i
,y
i
,z
i
тогда в кач-ве импульсов будут исп-ся обычн
проекц имп-ов.
U
N
i
i
p
m
E
1
2
2
1
Подставив в фор-лу(*)
i
pdVd
N
i
N
i
kT
U
i
p
mkT
N
N
z )
1
(*)
1
2
2
1
exp(
3
)2(!
1
dV=dxdydz,
z
dp
y
dp
x
dppd
. Как и
в случае ид газа инт-е по коорд можно отделить от инт-я по
имп-у. Потому что в класс физике энергию всегда можно
представить в виде кинетической зависящей только от имп-
а и потенциальной зависящей только от коорд.
*pd*)p
mkT2
1
exp(
)2(!N
1
z
i
N
1i
N
1i
2
i
N3
N
1i
i
dV)
kT
U
exp(
Если бы потенц энергия =0, то инт-л по коорд был бы
равен V
N
и мы получали бы стат сумму для ид газа
N
i
i
dV
kT
U
N
V
ид
z
1
)exp(
1
N
i
i
dV
kT
N
rrrU
N
V
k
1
)
)..
2
,
1
(
exp(
1
-конфигурац инт-л. Такое название от тогою, что
подинтегр сумма зависит от конкретного распол-я частиц в
пространстве. Используем сведение взаимод к попарному
