Термодинамика, проверочные работы по Василевскому
Подождите немного. Документ загружается.

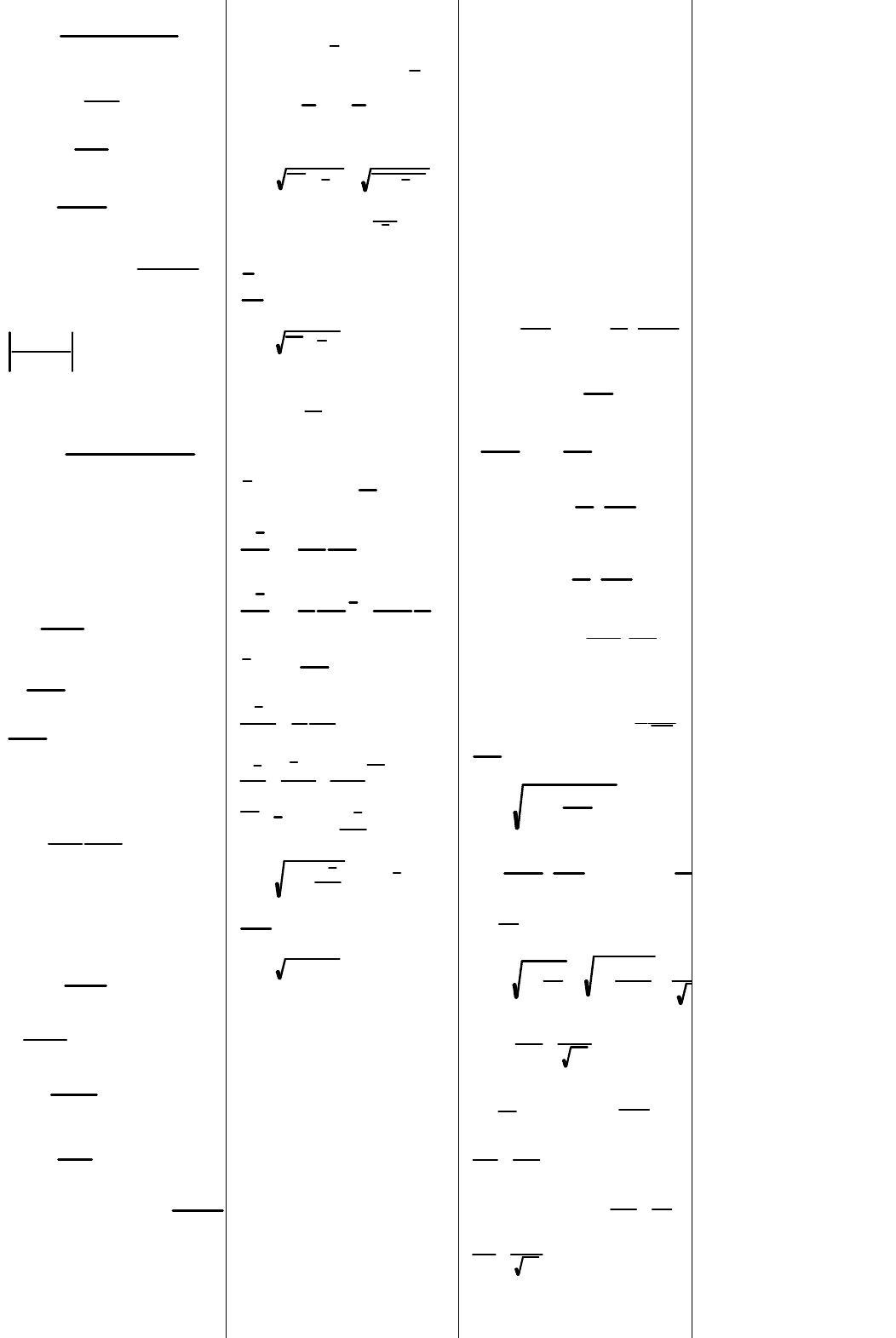
взаимод частиц.
ki
ik
rW
kTkT
N
rrrU
,
))(
1
exp()
)..
2
,
1
(
exp(
Сумма берется по всем парам част.
*))r(W
kT
1
exp(
12
))r(W
kT
1
exp())...r(W
kT
1
exp(*
1N,N13
Вместо одного множителя
)
)(
exp(
kT
rW
введем функц f(r)+1
или
1)
)(
exp()(
kT
ik
rW
ik
r
ik
f
. В силу сделанных предположений о слабой
неидеальности газа можно утверждать, что эта вел-на f
будет малой.
0
,1
)(
r
ik
r
kT
ik
rW
На
притягивательной ветви мала, на отталкивательной W и
тогда f будет =1. Но если воспользоваться моделью
твердого непроницаемого шарика, то эти тч вообще надо
исключить из инт-я. Мы их пока оставим ради математ
простоты записи, но только чисто формально
)
,..2,1(
exp(
kT
NrrrU
мы можем заменить произв-е членов.
)
1,
1)...(
12
1)(
11
1(
NN
fff
Далее перемножая скобки оставим только члены 0-го и 1-
го порядков
ik
ik
f
NN
fff 1
1,
...
1211
1
В данном приближении инт-л от экспоненц ф-ии заменяем
суммой инт-ов
N
dV
ik
ik
r
ik
f
N
i
i
dV
N
V
N
i
i
dV
ik
ik
f
N
V
k
1
)(
1
1
1
)1(
1
ki
ik
ikik
NN
N
ki
ik
ikikN
N
N
dVdVrfVV
V
dVdVrfdVdVdVV
V
)(
1
)(...
1
2
21
.
Все ф-ии f для каждой пары частиц одинаковы т.е.
одинаково зависят от расстояния между 2-я частиц,
поэтому в нашей сумме все слагаемые имеют одно и тоже
знач-е.
21
)
12
(
2
2
2
1
1 dVdVrf
N
V
Все слагаемые одинаковы и равны инт-лу для 1-й и 2-й
част.
21
)
12
( dVdVrf
),,,1,1,1(
12
)2,2,2,1,1,1(
12
rzyxrzyxzyxr
r- расстояние м/у частицами а и задают напр-е прямой
от 1-й част ко 2-й.
1ddrdsinrdV)r(f
V2
N
1k
2
1
2
2
drr)r(fddsindV
V2
N
2
1
2
2
drrrfV
V
N
2
)(4
2
2
2
1
Окончательный конфигурац инт-л:
)(
2
2
1 T
V
N
k
0
2
1)
)(
exp(4)( drr
kT
rW
T
22. Флуктуация ТД величин. Расчет флуктуаций
энергии с помощью канонического распределения.
Определение флуктуации ТД величины. Всякое
равновесное состояние задается с помощью макроскоп.
хар-к.
L
макро
L
- т.е. они средние величины
по внутр. движению.
LtL ~)(
-
принципиальное равенство.
LLtL )(
. Все макроскоп. х-
ки флуктуируют, беспорядочн. колебания около
равновесного значения. Иногда – это причина некоторых
явлений. Мерой 200флуктуации – серднеквадр. отклонение
величины.
2
)(
22
xxxx
x
.
Относительная флуктуация
x
x
x
.
Вычисление флуктуации с помощью канонического
распределения. Из ФСР известно что
i
W
i
LL
,
i
W
i
LL
22
,
2
2
LL
L
. Классический случай приводит к сложному расчету. И
лишь в некоторых случаях удобно. Например, для
флуктуации энергии.
dГ
kT
e
I
dW
/
1
)(
,
dГ
kT
eI
/
. Найдем
dГ
kT
e
I
dW
/
1
)(
,
dГ
kT
e
TI
dГ
kT
e
T
I
I
T
/
1
/
2
1
,
dГ
kT
e
I
kT
T
I
IT
/2
1
2
11
. Ранее мы показали что
Z
T
kT ln
2
. В классическом
случае используют интеграл I вместо суммы Z. Отсюда,
T
I
I
kT
1
2
. =>
2
2
1
2
2
kTkT
T
=>
T
kT
2
2
2
=>
T
kT
2
. Т.к.
U
и
V
C
T
U
, то
V
CkT
2
. Это бывает просто, т.к.
калорич. распредел. в класс. случае оказывается возможн.
записать как распред. вер-ти для энергии, поэтому вместо
многих перемен. коорд и имп. на деле только с одной
переменн. Также простая система, для которой C
V
знаем.
Флуктуация повышается с ростом T и чем больше N.
Относит. флуктуация с ростом N убывает. Эйнштейн
предложил рассчит. вероятности флуктуации в
равновесной системе через эту формулу.
24. Флуктуация объема. Флуктуация плотности.
Молекулярное рассеяние света. Изолир. адиабат.
система, внешние параметры const, =const, V=const,
система не полностью изолир. – т.е. она может совершать
работу. (Маленький цилиндрик с поршнем внутри). Пусть
у нас под поршнем в цилиндре масса газа m, где m<<M.
Пусть стенки цилиндра идеально теплопроводны. Т.е.
мгновенно пропускают любые кол-ва тепла. Тогда T=T
0
(среды). Поршень движется без инерции и трения.
Флуктуация сводится к тому, что объем массой m
изменяется на V. Вероятность этого dW(V), V=V-V
0
, где
V
0
– равновесное значение. Предположение: флуктуация
мала, так что T и p в среде остались практич. теми же
самыми. И внутри так же.
AAA
(работа m плюс
работа среды). Здесь
VpA
0
,
где
V
- изм. объема среды.
VV
, где V – изм. объема массы
под поршнем.
VpA
0
.
Процесс изотермич, а при нем
dFA
.
...
2
2
2
2
1
dV
V
F
dV
T
V
F
dF
. Здесь
p
T
V
F
,
T
V
p
V
F
2
2
=>
2
2
1
dV
T
V
p
pdVF
. p надо взять в точке равновесия (p
0
). Полная работа
системы
VpV
T
V
p
VpA
0
2
2
1
0
. Далее
dV
V
T
V
p
kT
econstVdW
2
2
1
)(
, где
0
VVV
. Это распад
вероятностей, которое есть нормальное гауссовское
распределение. А в нем формула 1.5.
2
2
2
1
x
x
e
,
22
xx
. В данном случае
T
p
V
kT
V
. Для идеал.
газа
2
1
p
RT
T
p
V
p
RT
V
p
V
. Флуктуация
N
V
a
N
V
RT
V
kT
p
V
kT
V
2
. Относит. флуктуация
N
V
V
V
1
. Флуктуация
плотности. Флукт. V тесно связаны с флукт. .
V
m
,
dV
V
m
d
2
.
V
dVd
. “-“ опускаем. Отн. флукт. = отн.
флукт. V выделенной массы в-ва.
NV
dV 1
~
,
N
d 1
~
, N – концентр. Эта флукт.
объясняет голубой цвет неба.
kxtEE
cos
0
. Если длина
волны велика, то в этом случае м. считать, что в пределах
V фаза одинакова. Если
d
, то
tEE
cos
0
. Вещ-во поляризуется,
дипольный момент
Ep
0
1
. Если
p
, где - малый V вещества. Всякий
переменный диполь излучает,
2
~
I
, где I –
интенсивность излуч. Т.к. в-во однородно, то связь I и E
везде одинакова. Поэтому волны когерентны, т.е. есть
усиление и ослабление по опред. направл. Поэтому
получаем только 2 волны в одном направлении, рассеяния
нет. Если есть неоднородносит в в-ве, то создается
рассеяние волны. Также
4
~
I
. Т.е.
рассеиваются прежде всего волны с большой частотой в
оптич. диапазоне, голубые волны. На больших высотах
неоднородности значительны, поэтому процесс излучения
сильный.
S
U
U
b
c
a
S
x
x=x
0
23. Формула Эйнштейна для вероятности флуктуации.
Ограничения на точность измерений, связанные с
наличием флуктуаций.
т
lnWkS
=>
kS
e
т
W
/
.Всякая
флуктуация связана с изменением энтропии в системе.
Пусть x – один или несколько параметров, которые
изменяются при флуктуации. Вероятность что x попадет в
[x,x+dx]
dx
xSxS
k
econstxdW
)]
0
()([
1
)(
, где
xx
0
- равновесное значение величины.
Значит нужно рассчитать изменение S, при изменении x от
x
0
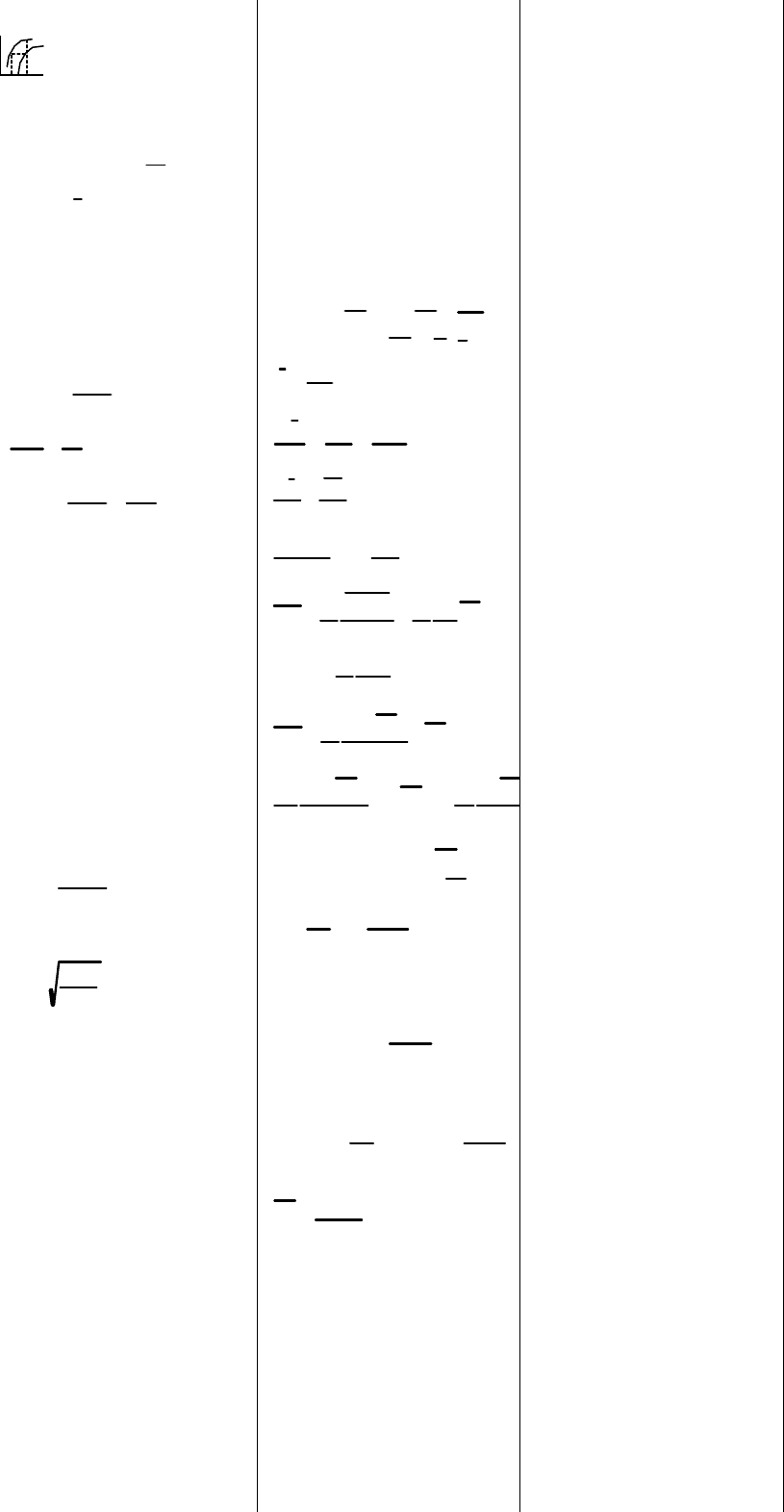
до x. Возьмем точку а и допустим, что произошла
флуктуация и при
0
xx
и
ca
. При
флукт. в равновесной изолир. системе энергия не
изменяется. При флуктуац. мы отходим от рвановес, т.е.
энтропия может только уменьшаться. Выделим состояние
b. S
b
=S
c
. Но для b x=x
0
, для c x. Переход b в c есть
равновесный адиабат. переход, при котором просходит
такое измен. x, которое возникло в рез-те флуктуации. В
нем
AU
. Можно связать U с S.
U
U
S
S
. Т.к.
TU
S 1
то
T
A
T
U
S
. Далее
dx
kTA
econstxdW
/
)(
-
формула Эйнштейна. Вероятность флуктуации опред.
работой равновесного адиабат. процесса при котором
имеет место такое же изменение параметра x, которое
возникло в рез-те флуктуации. Точность. Возьмем
динамометр. Пусть -отрезок порядка 0,1 цены деления. k –
жесткость.
kp
- оценка min груза,
который можно измерить. Значит для повыш. точности
нужно брать не жесткую пружину, но на слабой пружине
заметны флуктуации длины пружины. Пусть
x
- ср.
квадратичн. флукт. длины. Если
x
, то мы не
сможем отличить смещение стрелки под действ. легкого
груза от спонтанного смещ. в рез-те флукт. Вер-ть того, что
длина пружины x будет
dx
Tk
x
A
econstxdW
0
/
)(
, где
x
A
- работа адиабатич. растяж. пружины на
отрезок
x
. Работа растяжения
2
2
xk
x
A
.
2
2/
2
0
2/
2
x
x
e
Tkxk
e
, т.е.
k
Tk
x
0
, k
0
– пост. Больцмана. Прямой
способ повышения точности – охлаждение прибора. Если
флуктуация достигает порядка деления шкалы, то заметить
смещение в ре-те флукт. легко. XIX-XX веках флукт. очень
была важна.
25. Броуновское движение. Вывод формулы
Эйнштейна-Смолуховского. Связь броуновского
движения с диффузией и другими явлениями. БД –
беспоряд. движение малых частиц в среде жидк. или газа.
Оно резко противоречило II закону ТД, т.к. в рез-те вязкого
трения должно было остановиться. Но оно бесконечно.
Только теория флукт. объяснила БД. Но танец пылинок в
солн. лучах – это не БД, это родственное, т.к. вызвано
конвект. потоками. Истинное БД наблюд. и при
отключении конвекции. Одна молекула не может сдвинуть
пылинку как комар не сдвинет паровоз. Движение
объясняется флукт. давления по разные стороны от
пылинок. С одного бока меняется по разному, чем от
другого. Но это очень похоже на БД. Вывод. На движ.
частицу 2 силы:
aV
сопр
F
, где
ra 6
, r – радиус,
- коэфф. вязкого
трения. Также F – сила в рез-те флукт. давления по обе
стороны от шарика. Величина и напр. F хаотич. меняется с
теч. времени, не знаем F(t). Смещение частицы
)(tXxaxm
, где X(t) –
проекц. случ. силы. Проинтегр. невозможно, получим
средние. Пусть в поле зрения N>>1 частиц. Случ. сумму
X(t) можно исключить. Выходим на среднеквадр.
величины.
Xxxxaxxm
-
усредняем.
0 xXXx
.
i
f
N
f
1
,
dt
i
df
Ndt
fd 1
, т.е.
dt
df
dt
fd
- и для 2 пр-ных также.
dt
dx
x
dt
xd
2
)
2
(
,
2
2
1)
2
(
2
1
x
dt
d
dt
xd
xx
.
Дифф. еще раз
)
2
(
2
2
2
1
x
dt
d
, или
2
2
)
2
(
2
2
1
x
dt
xd
xx
. Получим
dt
xda
xm
dt
xdm )
2
(
2
2
2
)
2
(
2
2
. Степени своб. частицы попадают под действие теор. о
равном. распредел. энергии.
kTxm
2
.
Обозначим
Ux
2
,
m
kT
U
m
a
U
2
, пусть
Uf
. Общее решение ур-я будет
mat
eCf
/
1
. Частное решение положим
Af
0
,
a
kT
A
2
. Окончательно
akT
mat
eCf /2
/
1
.
Проинтегрировав, получим
2
2
/
)(
1
Ct
a
kT
mat
e
a
m
CU
, где C
2
=0, положив начало движ. отн. точки отсчета.
Первое слагаемое не дает ощутимый вклад, поэтому
t
r
kT
x
3
2
- ф-ла Эйнштейна-
Смолуховского. Обсуждение. Допускает простую эксп.
проверку. Т.е. измеряем x в поле зрения. Знаем T, r,
.
Опыты подтвердили закон. Для проверки достаточно
наблюдать одну частицу. И вид такой – зигзаги всякие.
Также если в нач. момент молекулы были в одном пр-ве,
открываем перегородку, найдем время возвращения в
первонач. объем. Это время резко возрастает с кол-вом
числа частиц. Если рассм. явл. убыли броун. частиц в
пределах нач. круга – диффузия. Сущ. связь коэфф.
диффузии с коэфф. вязкости. Есть также распред. броун.
частиц в поле силы тяжести по высоте. Потоки вверх и
вниз уравновешивают друг друга.
1.Идеальный газ в МКТ. Вывод распределения Максвелла.
2.Вычисл. давл-ия на стенку сосуда.
3. Квазинезависимые подсистемы.
4. Макр-ое сост. с-мы
5. Определение энтропии и ее свойства. Закон возрастания
энтропии в замкнутой системе.
6. Связь энтропии с числом микросост. в локально-
равновесных системах. Принцип Больцмана и ф-ла
Больцмана. Статист. толкование закона созраст. энтропии.
Пример примен. метода Больцмана.
7. Равновесный процесс. Статистическое определ. T,
хим.потенц, p. Основное ТД р-во-н-во. Статфизика и ТД.
8. Вывод формулы канонического распределения.
9. Особенности и св-ва канонического распределения.
Вычисление ТД величин с помощью КР.
10. Приближенное выражение для статистической суммы.
Приближенное выражение для числа квантовых состояний.
Классическое каноническое распределение.
11. Расчет статистической суммы для классического
одноатомного идеального газа. Нахождение ТД ф-ций и ТД
ур-я состояния системы
12. Распределение Максвелла-Больцмана. Распределение
Максвелла и его свойства. Распределение для модуля
скорости и энергии частицы. Распределение Больцмана.
Барометрическая ф-ла.
13. Реальные газы. Модель слабонеидеального газа.
Вычисление конфигурационного интеграла.
14. Ур-е сост-я слабонеидеаль-го газа. Сравнение теоритич
ур-я сост-ия с ур-ем В-д-В..
15. Теорема о равномер-м распр-ии энергии сс. Док-во ее.
16. Классич-я теория теплоемкости. Затрудн-я этой теории.
Простейш-я квантовая теория теплоемкости твердого тела.
Теплоемк-ть газов в свете квантовых представлений.
17. Распред-е Ферми-Дирака и Бозе-Энштейна.
18. Распределение Больцмана и критерии вырождения газа.
Распредел-ие час-ц в квант-х ид. газах по энергии.
19. Вырожденный фермион. газ. Электроны в металлах.
20. ЭМ излучения как фотонный газ. Формула Планка.
21. Законы равновесного ЭМ излучения. Излучение АЧТ.
Уравнение состояния фотонного газа. Функция Стефана-
Больцмана для интегральной плотности энергии.
22. Флуктуации термодинамических величин. Расчет
флуктуаций энергии с помощью канонического
распределения.
23. Формула Эйнштейна для вероятности флуктуации.
Ограничения на точность измерений, связанные с
наличием флуктуаций.
24. Флуктуация объема. Флуктуация плотности.
Молекулярное рассеяние света.
25. Броуновское движение. Вывод формулы Эйнштейна-
Смолуховского. Связь броуновского движения диффузией
и другими явлениями.
