Тер-Саркисов P.M. Разработка месторождений природных газов

Подождите немного. Документ загружается.

ношением,

учитывающим скорость фазового перехода "адсорбтив

—

адсорбат".

В условиях реального газоконденсатного пласта вдали от забоев сква-

жин скорости фильтрации невелики и имеют порядок величин 10~

м/с, а

безразмерный параметр Блэкуэлла составляет при этом 8v/D

< 10~\ т.е.

на

практике можно не учитывать явления конвективного перемешивания

(см.

рис. 2.73) и кинетики сорбционных процессов на фронте вытеснения

газа газом.

Методика исследований

Исследования выполнялись автором совместно с В.А. Николаевым приме-

нительно к условиям опытного участка Вуктыльского

НГКМ,

истощенного

до давления порядка 5 МПа.

Схема экспериментальной установки представлена на рис. 2.74.

Уста-

новка включает сменную модель пласта, а также оборудована отводом для

отбора проб газа при анализе на "внешнем" хроматографе несорбирую-

щихся компонентов (не разделяющихся на колонке хроматографа БОТА-

На).

Эксперименты по оценке длины зоны смеси газ — газ выполняли с

применением

двух

моделей пласта, имеющих параметры:

Номер модели 1 2

Длина, м 5 20

Пористость т, доли

0,222

0,260

Проницаемость К-10~

, м

14 30,6

Размер частиц

810~

м 1 1,5

Объем пор

V10"

0,59 3,40

Целью выполнения первой серии экспериментов было определение

коэффициентов

извилистости £ пористых сред моделей пласта, на кото-

рых впоследствии предполагалось провести эксперименты по оценке дли-

ны

зоны смеси углеводородный газ — метан. Для определения ^ использо-

вались такие слабо сорбирующиеся при низком давлении (порядка 5 МПа)

газы, как азот и двуокись

углерода.

Расчетное значение коэффициента

взаимной диффузии этих веществ при давлении 5 МПа составляет D

3,010~

/с. Для исключения зависимости эффективной диффузии от

Рис. 2.74.

Схема

установки:

— пресс ИП-6; 2 — вентиль; 3 — пробоотборник; 4 — баллон с метаном; 5 — манометр

образцовый; б —

сосуд

PVT; 7 — модель пласта; 8 — хроматограф (БОТАН); 9 — отбор про-

бы газа при анализе несорбирующихся компонентов; 10 — счетчик газовый; 11 — сепаратор

201

скорости фильтрации v эксперименты проводили при низких (пластовых)

значениях v, при которых выполнялось соотношение

5v/D

< КГ

(2.46)

Для определения коэффициентов эффективной диффузии по экспери-

ментальным данным использовали известное решение в безразмерном

виде:

эс,

эс, _

д.э

с,

•Г

1?~

где т, х, С, — безразмерные время, линейная координата и концентрация;

— длина модели пористой среды с граничными и начальными условиями,

соответствующими условиям проведения опытов:

С,(0, т) = 1; С,[х, 0) = 0.

Решение

(2.47)

приводит к соотношению В.Н. Николаевского

•

(2-48)

Это соотношение аналогично предложенному Дж. Аронофски

где у

D/vl; 1 — длина перемешивания.

Соотношение позволяет по

углу

наклона кривой изменения концент-

рации

компонентов на

выходе

из модели пласта в зависимости от безраз-

мерного времени определять коэффициенты эффективной диффузии ком-

понентов смеси.

Результаты исследований

Серия

экспериментов по вытеснению двуокиси

углерода

азотом, а также

азота двуокисью

углерода

позволила определить коэффициенты извилисто-

сти | моделей пористых сред.

Вначале были найдены с использованием описанной выше методики

(по

углу

наклона экспериментальных кривых изменения концентрации од-

ного газа в смеси в процессе вытеснения его

другим

газом) значения ко-

эффициентов

эффективной диффузии. Затем по соотношению (2.45), ис-

пользуя известные значения взаимной молекулярной диффузии несорби-

рующихся газов (азот - двуокись углерода), получили коэффициенты из-

вилистости ^.

Результаты экспериментов по вытеснению двуокиси

углерода

азотом и

азота двуокисью

углерода

при давлении 5 МПа представлены ниже.

Номер

модели 1 2

v-ЮЛ м/с 10 5 10 5

D10"

/с 2,90 2,84 3,10 3,13

- 2,09 - 1,93

Эксперименты показали, что при вытеснении двуокиси

углерода

азо-

том и, наоборот, азота двуокисью

углерода

при одинаковых скоростях

202

фильтрации

v = 10

м/с получаются практически одинаковые (с точностью

5 %) значения коэффициентов диффузии. Средние их значения для пер-

вой

модели D =

2,9-10~

м/с и для второй модели D =

3,110~

м/с. При

меньших скоростях фильтрации v = 5 • 10~

м/с те же коэффициенты со-

ставляют D =

2,8410~

/с для первой и D =

3,13-Ю"

/с для второй

модели. Таким образом,

результаты

экспериментов

подтверждают

незави-

симость коэффициентов эффективной диффузии от скорости фильтрации

при

выполнении соотношения (2.46).

Представляют интерес полученные с использованием диффузионной

модели коэффициенты извилистости пористых сред. Величины %, оказались

существенно большими, чем принимают обычно, исходя из гидродинами-

ческой модели: | = 2,09 для первой модели пласта и £ = 1,93 для второй

модели пласта.

При

выполнении экспериментов по вытеснению углеводородной газо-

образной

смеси

сухим

газом (метаном) использовались установка и мето-

дика, аналогичные описанным выше.

Составы равновесных фаз вуктыльской пластовой углеводородной си-

стемы при давлении 5 МПа и исходный состав системы (при давлении

37 МПа) приведены в табл. 2.20. Поскольку в составе равновесной газовой

фазы

при данных условиях (5 МПа) преобладает метан, а содержание каж-

дого

из компонентов фракции С

в смеси не превышает 10 % (этана —

9,56, пропана — 4,06 % и т.д.), то влиянием компонентов

друг

на

друга

при

рассмотрении диффузионных процессов (и использовании коэффициентов

диффузии) можно пренебречь [41].

Как

и в экспериментах с несорбирующимися газами, вытеснение

угле-

водородного газа

сухим

(метаном) проводили при скоростях фильтрации,

равных 510~

м/с. Таким образом, и в этом

случае

влияние кинетики

сорбции

на форму фронта практически исключалось.

Таблица 2.20

Состав

вуктыльского

пластового

газа

(молярные

доли,

исходного

состава

равновесных

фаз

системы,

истощенной

до

давления

5 МПа

Углеводород,

параметр

Метан

Этан

Пропан

Изобутан

Бутан

Пентан

Гексан

Гептан

Нонан

Додекан

Гептадекан

Сумма

Пентаны

плюс

высшие

Молярная

масса

пентанов

(г/моль)

ГКФ

(г/м

)

Давление,

МПа

Система

79,10

8,80

3,90

0,60

1,20

1,05

1,26

1,84

1,15

0,64

0,46

100

6,40

115

327

Газовая

фаза

83,19

9,56

4,06

0,48

1,10

0,63

0,50

0,40

0,07

0,0052

0,0001

100

1,60

86,6

58,5

Жидкая

фаза

16,23

6,45

6,85

1,96

4,35

5,92

10,32

18,07

14,01

8,90

6,94

100

64,16

126,4

—

203

Рассмотрим методику построения изотерм адсорбции из эксперимен-

тальных данных по вытеснению

сухого

газа газовой смесью. Предполо-

жим, компонент i смеси газов не сорбируется. Тогда, основываясь на до-

полнительной информации о коэффициентах молекулярной диффузии

данного компонента в смеси и зная свойства пористой среды, можно вы-

числить коэффициент эффективной диффузии по соотношению (2.45).

Полученная величина D^. позволяет построить гипотетическую форму

фронта вытеснения в

случае

несорбируемости компонента (рис. 2.75, кри-

вая /). В действительности, однако, компонент i сорбируется пористой

средой, и поэтому фактически определенная из эксперимента кривая

фронта вытеснения (кривая 2)

будет

смещена вправо и иметь более поло-

гий наклон, зависящий от формы изотермы сорбции. Чтобы определить

количество сорбированного вещества, например, при концентрации его в

газе С/, достаточно определить заштрихованную площадь

между

двумя

кривыми 1 и 2 (см. рис.

2.75).

Аналитическое выражение для (оценки) заштрихованной площади

имеет вид

(2.49)

C,(x)dT-

где С,,, C

— функции относительной концентрации компонента i на вы-

ходе

из модели пласта для идеального (в отсутствие адсорбции) и реального

случаев соответственно.

Отсюда величина адсорбции /-го компонента а, (моль/м

), отнесенная к

единице объема пористой среды, равна

,(С,)

С,(т;-т,) +Jc,,.(T)dT -Jci(T)dT,

(2.50)

где величины С,, и С

, имеют тот же смысл, что ив уравнении (2.48), но

выражены в "абсолютных" значениях (моль/м

Многочисленные эксперименты показывают, что форма фронта при

малых и больших значениях С сильно деформирована. На рис. 2.75 изоб-

ражен типичный для углеводородов случай, причем с увеличением размера

молекулы компонента смеси соответствующая кривая все заметнее откло-

няется от симметричной S-образной кривой для гипотетического случая.

Принципиально

возможно изменение формы фронта вытеснения под

влиянием кинетики фазового перехода "адсорбтив— адсорбат". Описанные

С,

с;

1ч' т'

IX, X,

Рис.

2.75.

Изменение

концентрации

компо-

нента

i в

выходящей

из

пористой

среды

сме-

си:

/ — компонент i не сорбируется; 2 — ком-

понент

i сорбируется пористой средой

204

опыты были повторены при

других

скоростях фильтрации, еще более

низких (~ 10~

м/с), и результаты обеих серий экспериментов совпадали;

отсюда можно сделать вывод, что в условиях описанных экспериментов

скорость установления адсорбционного равновесия компонентов достаточ-

но

велика.

На

рис. 2.76, 2.77 представлены экспериментальные графики зон смеси

для компонентов С

, изо-С

, н-С

, С

по результатам опытов на моделях

пласта номер 1 и 2 (см. табл.

2.20).

На рис. 2.78 представлены изотермы

сорбции компонентов смеси следующего состава (в мольных %) в моделях

пористых сред 1 и 2 (см. табл.

2.20):

С, - 79,5; С

- 9,0; С

- 6,0;

изо-С

- 2,2; н-С

- 1,8; С

- 1,5.

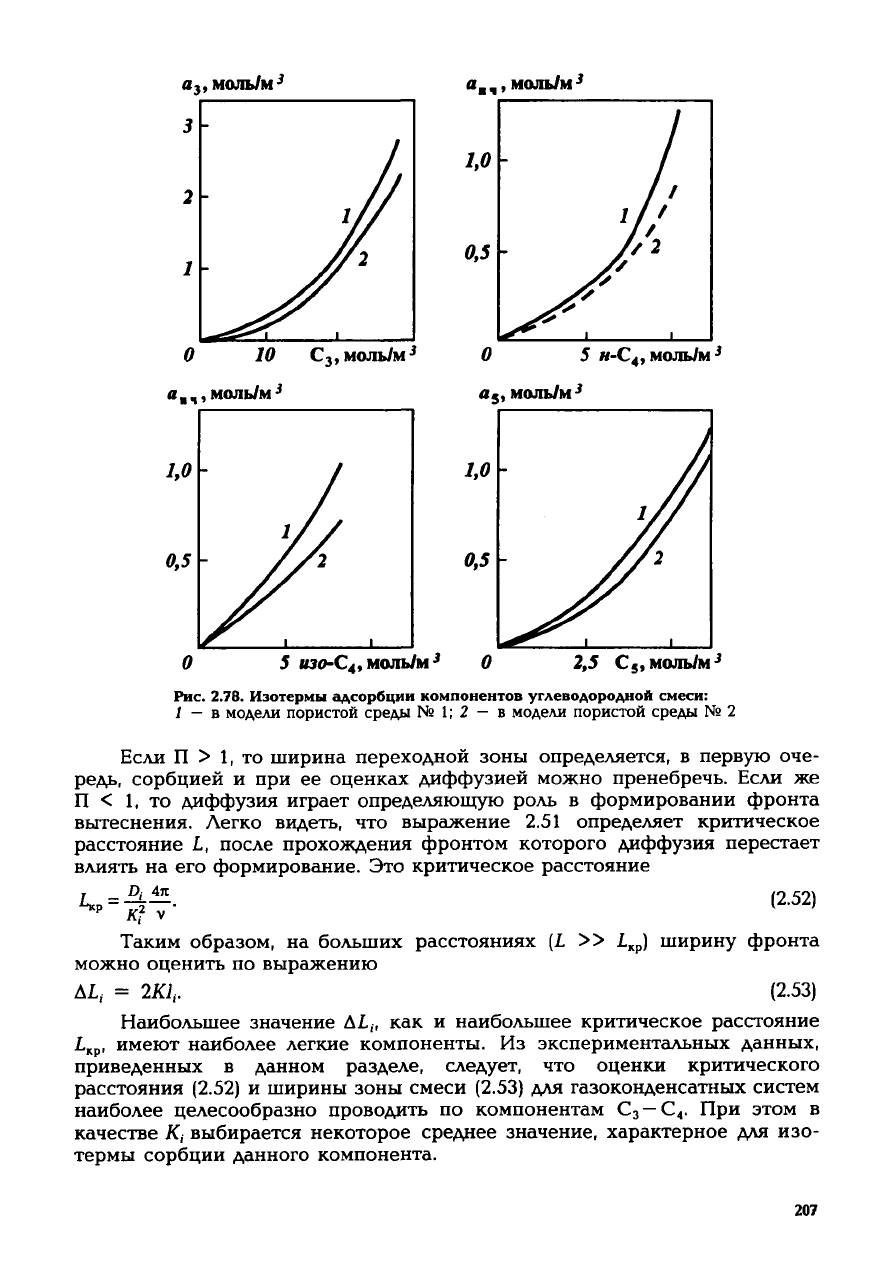
Из

рисунков видно, что изотермы сорбции, особенно наиболее тяже-

лых компонентов, существенно нелинейны. Резкий подъем вверх изотерм

с ростом величины С связан, по-видимому, с началом конденсации компо-

нентов.

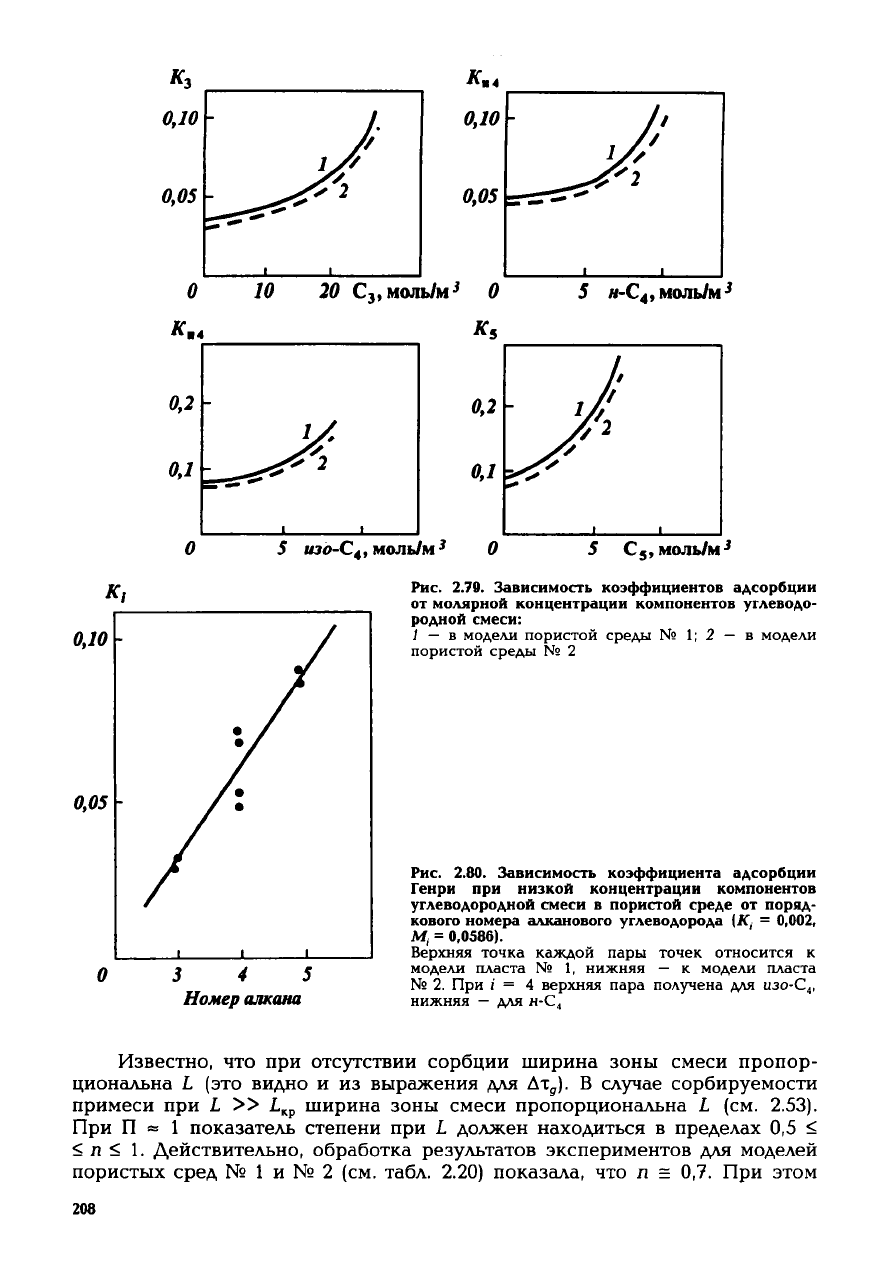
На

рис. 2.79 изображены зависимости коэффициентов адсорбции

К, =

a.fCJ/C,

от плотности вещества i в пористой среде (в моль/м

). Видно, что при низ-

ких плотностях коэффициент адсорбции не зависит от величины С, и, сле-

довательно, при этом вполне допустимо линейное приближение Генри.

Значения

K°=Kj\

коэффициентов адсорбции при низких парциальных

давлениях компонентов изображены на рис. 2.80 в виде зависимости от

размера молекулы углеводорода. Однако с ростом плотности сорбируемого

компонента величина К, становится существенно зависящей от величины

. Таким образом, соотношение Генри

) =

далеко не всегда можно использовать в практических расчетах процессов

вытеснения.

Как

следует

из изложенного,

следует

из

угол

наклона кривой С, (см. рис.

2.75) определяется диффузией ком-

понента i и его свойством сорби-

роваться данной пористой средой.

Ясно,

что при достаточно больших

коэффициентах Генри К, и доста-

точно малых коэффициентах диф-

фузии D^. ширина фронта вытес-

нения

будет

определяться в первую

очередь сорбцией компонентов сме-

си.

Интересно получить критерий

Рис. 2.76.

Динамика

молярной

массы

про-

дукции

при

вытеснении

метана

газовой

сме-

сью из

модели

пласта

длиной

5 м (а) и 20 м

(б);р = 5МПа, Г=20°С.

Состав газовой смеси, % (молярные доли):

С, -

83,04;

- 9,48; С

- 4,29;

изо-С

0,48; н-С

- 1,11; С

- 1,60

М,

г/моль

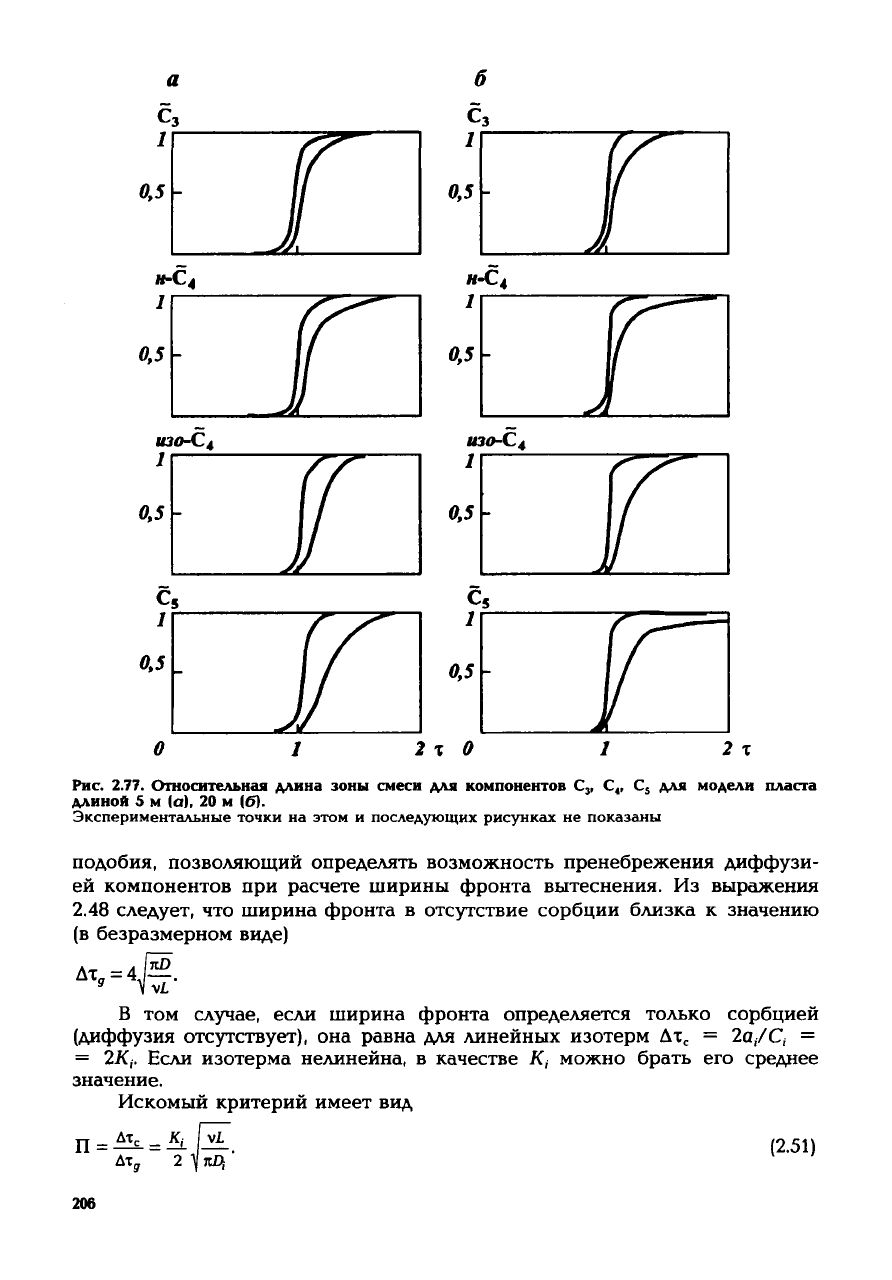
Рис. 2.77.

Относительная

длина

зоны

смеси

для

компонентов

С,, С

, С

для

модели

пласта

длиной

5 м (а), 20 м (б).

Экспериментальные точки на этом и последующих рисунках не показаны

подобия, позволяющий определять возможность пренебрежения диффузи-

ей компонентов при расчете ширины фронта вытеснения. Из выражения

2.48

следует,

что ширина фронта в отсутствие сорбции близка к значению

(в

безразмерном виде)

В том случае, если ширина фронта определяется только сорбцией

(диффузия отсутствует), она равна для линейных изотерм Дт

2а,/C

2Kj. Если изотерма нелинейна, в качестве K

можно брать его среднее

значение.

Искомый

критерий имеет вид

Дт

Дт„

(2.51)

206

, моль/м *

5 н-С

, моль/м *

а,,,

моль/м

взо-С

моль/м

2,5

, моль/м

Рис.

2.78. Изотермы

адсорбции

компонентов

углеводородной

смеси:

) — в модели пористой среды № 1; 2 - в модели пористой среды № 2

Если П > 1, то ширина переходной зоны определяется, в первую оче-

редь, сорбцией и при ее оценках диффузией можно пренебречь. Если же

< 1, то диффузия играет определяющую роль в формировании фронта

вытеснения. Легко видеть, что выражение 2.51 определяет критическое

расстояние I, после прохождения фронтом которого диффузия перестает

влиять на его формирование. Это критическое расстояние

= -L-.

(2.52)

Таким образом, на больших расстояниях (I >> 1

хр

) ширину фронта

можно оценить по выражению

AL,

= 2К1,.

(2.53)

Наибольшее значение Л1„ как и наибольшее критическое расстояние

кр

, имеют наиболее легкие компоненты. Из экспериментальных данных,

приведенных в данном разделе,

следует,

что оценки критического

расстояния

(2.52)

и ширины зоны смеси

(2.53)

для газоконденсатных систем

наиболее целесообразно проводить по компонентам С

— С

. При этом в

качестве /С, выбирается некоторое среднее значение, характерное для изо-

термы сорбции данного компонента.

207

10 20 С

моль/м

H-C

,MOJ\IJM

-4»

изо-С

моль/м

5 С

моль/м

0,10 •

Рис.

2.79. Зависимость коэффициентов

адсорбции

от

молярной

концентрации

компонентов

углеводо-

родной

смеси:

/ — в модели пористой среды № 1; 2 — в модели

пористой

среды № 2

4 5

Номер

алкана

Рис.

2.80. Зависимость коэффициента

адсорбции

Генри

при

низкой

концентрации

компонентов

углеводородной

смеси

пористой

среде

от

поряд-

кового

номера

алканового

углеводорода

(К, = 0,002,

М,

= 0,0586).

Верхняя точка каждой пары точек относится к

модели пласта № 1, нижняя — к модели пласта

№

2. При i = 4 верхняя пара получена для изо-С

нижняя

— для н-С„

Известно,

что при отсутствии сорбции ширина зоны смеси пропор-

циональна

L (это видно и из выражения для Ах

). В случае сорбируемости

примеси

при L » 1

кр

ширина зоны смеси пропорциональна L (см. 2.53).

При

П я 1 показатель степени при L должен находиться в пределах 0,5 <

< п < 1. Действительно, обработка результатов экспериментов для моделей

пористых сред № 1 и № 2 (см. табл. 2.20) показала, что п = 0,7. При этом

208

для модели № 1 (I = 5 м) П = 0,88, для модели № 2 (I = 20 м) П =

1,76, а 1

кр

= 6,5 м (расчеты проведены по пропану). При аналогичных

условиях в пласте критерий

будет

принимать большие значения, так как

характерные расстояния существенно превышают 1

кр

= 6,5 м.

Таким образом, формирование фронта вытеснения в газоконденсато-

насыщенных пластах происходит под влиянием

двух

процессов: диффузии

сорбции. Сорбируемость компонентов пластовой смеси может привести

тому,

что фактором, определяющим форму и ширину фронта вытесне-

ния,

является сорбция; в этом

случае

выполняется соотношение П >> 1. В

то же время при П ~ 1 ширина фронта зависит от пройденного расстояния

как

L", причем показатель степени п может варьировать в

пределах

0,5 <

< л < 1, что и

подтверждают

эксперименты.

Использование формулы

(2.53)

и данных рис. 2.80 позволяет оценить

длины зон смеси как для отдельных компонентов вытесняемой пластовой

равновесной газовой фазы, так и для этой фазы в целом. Например, для

этана, пропана, бутанов, пентанов длины зон смеси составят соответствен-

но:

при пройденном фронтом вытеснения расстоянии 500 м около 1,5, 29,6,

57,6, 85,7 м; при пройденном расстоянии 1000 м около 3,1, 59,2,

115,2,

171,4 м. Для пластовой газовой фазы (по фракции С

) соответствующие

длины зон смеси

будут

равны 24,4 и 48,7 м, т.е. составят около 5 % рассто-

яния

между

нагнетательной и добывающей скважинами.

Оценка длины зоны смеси по формуле

(2.53)

дает

наименьшие значе-

ния

этого параметра, которые

следует

использовать при определении мо-

мента начала контроля за прорывом нагнетаемого газа к добывающим

скважинам. Учитывая

результаты

исследований по испаряемости компо-

нентов С

в прокачиваемый газ, а также существенное отличие ожидаемо-

го коэффициента

охвата

пласта от единицы, при составлении, например,

регламента на закачку

сухого

газа необходимо предусмотреть

соответству-

ющие мероприятия контроля на добывающих скважинах в расчетные пе-

риоды времени после начала закачки газа.

2.5.4

Математическое описание процесса вытеснения

пластовой газоконденсатной смеси

сухим

газом

Развитие методов численного моделирования и современной электронно-

вычислительной техники позволяет эффективно решать реальные задачи

многокомпонентной фильтрации.

Математическое описание процессов фильтрации пластовых флюидов

сводится к решению краевых

задач

для системы нелинейных дифференци-

альных уравнений в частных производных.

Точные или приближенные аналитические решения этих задач, при-

годные для практического использования, можно получить для фильтраци-

онных потоков простой геометрии и при использовании различных упро-

щающих предположений о механизме процесса. Однако большинство ре-

альных фильтрационных потоков имеют сложную форму и описываются

системами нелинейных дифференциальных уравнений, получить аналитиче-

209

ское решение которых невозможно; эти уравнения решаются приближен-

ными

численными методами с использованием ЭВМ.

При

построении численной модели и алгоритмов используется дис-

кретное представление переменных и дифференциальных операторов

уравнений,

а также области течения.

Используя допущения о локальном термодинамическом равновесии

фаз,

справедливости обобщенного закона Дарси, пренебрегая малым влия-

нием

капиллярных, диффузионных сил и гравитацией, изотермическую

фильтрацию многокомпонентной смеси можно описать следующей систе-

мой

дифференциальных уравнений:

div(kh В,

grad

р) = ^-{mkN z,), i =~l,

где

м)

N=SJ^-

+ (l -

S)-g-; (2.54)

= 1 - 5

Уравнения

(2.54)

являются уравнениями баланса количества каждого из

компонентов

в дифференциальной форме. Суммируя уравнения для ком-

понентов

и заменив последнее уравнением баланса общего количества сме-

си

случае

тонкого горизонтального пласта в пренебрежении вертикаль-

ным

движением флюида, получаем эквивалентную систему:

div(kh В,

grad

р) = 7nh-^-(Nz,), i = 1, 1-1;

div(kh В

grad

p) = mh

&±, (2.55)

где

В = Ев„

Введенные величины связаны дополнительными соотношениями:

—(I-V)P,M«—

(25б)

где v — корень уравнения 2 '^~ '*' = 0;

i=l l +

(Kj-\)v

I l

У1

Sx,M,; K

i=l

i=l X,

условиями нормировки состава

При

описании модели используются следующие обозначения: К, —

константа

равновесия г-го компонента; z, — мольная доля /-го компонента

210