Тарг С.М. (ред.). Теоретическая механика. Методические указания и контрольные задания
Подождите немного. Документ загружается.


Пршмер
Д2.
К верпакалlьной
плите
I
массаft
m,
с помоIIFю
невесо-
мого
стержня BD
длпtной
/ прикреплен
груз
D
массой
m,
(рис.
Д2а).
В мо-
мент
времени
t
о
-
0
стержень
начинает
вращаться вокруг
точки
В так,,
Рис.
Д2а
что
расстояние
s
=
,tb
изменяется
по закону
ý
=
F
(t),
где
s
-
в
метрах,
I
-
в
секундах.
Плита
движется
по
горизон-
талъным нЕшравлrяющим
и при
fo
=
0
еескоростьц=цо.
Дано:
m|=12кг,mr=6кг,
I=0,8M,
tr=2c,
uо=0,
s=+
(3-r2).
(1)
l.
Определение
перемещеншяxt
tIпитызавремяотfо
=
0до
t
=tr.
Решение.
Рассмотрим
механическую
систему, состоящую из
IIлиты
и груза.
Изобразим
действуюшs{е
на нее внешrме силы:
силы
тяжесм
V,F,
и суммарную
реакц}Iю
Fнаправпяюц-рIх. Проведем
коорш{натные
оси
ху
так,
чтобы ось
у
прошла
через
начапьное
положение
центра
масс
плиты.
Для
определения
xt
восполъзуемся
теоремой о
движении
шентрd
масс
С
спсrемы и
составим
шrфференIцdальное
уравнение
его
дрижения
в
проек[ии на ось
х,
обозначая
массу
системы
через
r!:
*ic_ Z
Ff,х,
или
*}с
-
0,
так
как
ZFf"=ptx*pzx*Nx_0.
Икгегрируя
это
уравнение,
получим
-}с=
Сr,
furс=
Crt
+
С2,
где cr
и
С,
-
постоянные
интегрирования.
Из
формулы,
определяющей
абсlшссу
)16,
центра
масс,
спедует, что
для
рассматриваемой
системы
mхс
-
mrx *
mrхр,
где
х
-
абсцисса
цент-
ра
масс ппиты,
определяющiш
одновременно ее
положение,
хD
r
абсrисса
груза D.Из
рис.Д3а
видно,
что
xD=
х
-
I
sin
9,
где
где
}= ч
скоростъплиты.Поначалънымусловиямприf
=0
Х=0,
*
=
чо
=
0.
Подставив
эти величины
в
равенства
(5)
и
(4),
полrмм С,
=
0,
С2
=
-mrL
При
найденных
значениях
С|
и С2 из
равенства
(4)
оконча-
телъно
получим
(m,+m,)i
-+.lп2lsin
(+)
=.,,
х=
-
m'l
Г'-соs
(
llt|+lll,
L
t
(5)
{)]
Этот
резулътат
дает
зависимостъ
х
от
f
.
Полагая
здесъ t
=
t,
=2
с,
нЙдем
искомое
перемещение
xl
.
О
т в е т:
xl
=
-0,4
м
(плита
переместится
влево).
2.
Определение
скорости
tl
|.
При
тех
же
условиях
(1)
найдем
ско,
рость
иl rйиты
в
момент
време}r.{'
l
=
2
с.
Решение.
Рассматриваем
опять
механическую
систему, состоящ{р
из плиты
и
грузL, и изображаем
действуюцие
на нее внешние
силы
Pt, Р2
и
peaкImlo
Й
провод}rм
оси
ху
(рис.
Д2О1
.
Для
определения
u
t
восполЬ
зуемся
теоремой
об изменении
количестъа
движения
системы,
уЧитывая,
что
дJIя
рассматриваемой
системы
О
-
0tШ
+
QD,
где
0-'=
mri
^0D
=
=
tttrip
-
количества
движеrIия
плиты
и
груза соответственно.
Состirвляя
урzл,внение
в проекIши
на осъ
х,
получим
dQx
о
dQx
=zFf*,
иJIи
."
=0,
!
dr
^"l'
dr
так
как
ZFf*=Pl
x*Pzx+Шx-0.
Отсюдд следует, что
Qх=O,Р
*аР
-0
или
lп
|ч
х
+
lll
2uDx
=
С
r.
(6)
Рис.
Д2б
Jlпя
опредеIIекия
u
Dx
рассмотриМ
ДВиЖеНИе
ГРУ3а КаК
СЛОЖНОе,
СЧИ,
тая
его
движекие
по
отноше}мю
к
tIпите
относительным,
а
движеНио
с8,
мой плиты
-
переносным
движением.
Тогпаф
=
Й*р
*iioTH,
ГДе
ЧисЛеН,
но
uпер
=
и
И
UoTH,=
;.
Покажем
вектор iorn
}Ia
рис.
д2б,
направив его
перпенд.rкулярно
BD
в
с:орону
положителъного
отсчета
ý
или
9,
и
опреДе-
лим проекщrю
вектора
uд
на ось
х; получим
uд"
-
цу
_
UoTH
cos9,
где
ý
т
^
lT
Ttz
9=т=?(з-12
1
исоý9=соst;
--r)
=sin{+)
(7)
В
дшноЙ
задаче v
Dx
можно
еще
найти,
опредеJIив
абсtрtссу точки D,
Т.е. Хр
=
Х
-
I
sin,p
ФЙ.
Д2а);
тогда uDx-
;D
=;
-
Iicos
9,
где
}=u*,
Ii
=
i,
а
значение cos *p
дает
равенство
(7)
.
41
п
(2)
{+}
(з)
В
резупътате,
найдя значение
mхс
и
подстilвив
его в
(2),
попучим
(m,
+
mr)х
-
m"/cos
(*
)
=a,
t
+
С2.
(4)
,Сrо
ý
Е
д
l
l
h
а
х

(mt
+
m,)ч
*
m,+
f
sin
lЧ
J
\6
По
начuIьЕым
условиям
при f
=
тепьно из
(8)
наход{м
При
наЙденном значении
v
Dx
равенство
ds Tl
а
UoTH
=
о,
=
-
э
r, примет
вид
(6)
,
есJIи
r{есть,
что,их
=
ц,
[ано:
дополнителъно
к
усло-
ВИЯм
(l):
сл.Jо
=
5
с-',
М
=
kt,
где /с=
=
l0
Н
.м/с.
О
п
р
е
д
е
л
и т ь:
ц)=f(t)
*
зави-
симость
угловой
скорости
плитьt
от
време
ни.
Решение.
Рассм
отрим
м
еханичес-
кую
систему, состоящую
пз
плиты
и
груза
D,
и изобразим
действуюu${е
на нее
внешIние силы
: силы
тяжести
F,
Fr,
реакции
-П1
п
Еg
поппятника
н
подшипника и
вращаюrций момент
|,LH
,.
Rн
}...r.
"u
tH
I,
RЕ
8(
(
с|
д
п
Е
F,
(10)
на
d' и интегрируя, пол}чим
(l1)
(
12)
)=
0u
с|.
=
0,
что
дает
С,
(8)
=
0, и
oкotпIa-
ll=
-
m2
Tl
f
sin tt \.
m|+mz
Э
\
б
l
Этот
резупьтат
опредепяет
зaвисимость
и
от
f.
Полагая
здесь
t
=
f
л
=
=
2
с, наftдем
искоi,ttю
скорость
и
l
.
О Т
в
е
т:
ч
|
=
_0,48
м/с
(скоростъ
направлена
влево) .
3.
Определение
реакции
Л/r.
При
тех
же
условиях
(1)
найдем
реак-
щ{юЛ/,
направляюцихвмоментвреме}ц{f
,
=
2с.
Решение.
Опять
рассмотрим
механическую
систему,
состоящLю из
плиты и
груза
D,
н
изобразкм
действуюцие
на
нее
внешние силы
Р|,
Р2
и
реакцию
Л/
(рис.
Д2а).
Для
определения
ff,
восполъзуемся
теоремой о
движении центра
масс
системы
и составим
дифферекциалъное
уравнение
его
движения
в
проекIши
на
осъ
у:
^'iC
=
z Ffy
или
^ic=
fry'
-
Р|
-
Рr,
тде
m
-
масса
системы;
Р|
-
mtgiP,
-
mzg.Из
формулы,
определяющеЙ
ОРДИНаТУ
У
g
ЦеНТРа
МаСС
СИСТеМЫ,
СЛеДУеТ,
ЧТО
ДЛЯ
РаССМаТРИВаеМОfi
системъ,
m!с
=
mryCt
+
lпzyD,
гд9, как видно из
рис.
Д2а,
yCt
-
h,
7D=
2h
-
/
cos
g.
Тогпа,
испопъзуя
равенство
(7),
полrим
lпt2\
myC=mrh+Zmrh-mrlsin
I
u
J.
Вьнисляя
производные и
учитыв€uI,
что
h
=
сопst, попупlим
hlc.
Д2в
М.
Для
определения
l,
примеким теорему
об
изменении
кинетического
момента
системы относителъно
оси
z.
Препварительно_заметим,
что так
как
.ип",
{
n
F,
парirллель}Iы
оси
z,
8
реак[ц{и
F,g
п R,ц
эту
осъ
пересе-
кают, то их моменты
относительно
осн
z
равны
нулю.
Тогда
Z
tп,
tFfl
=
=
||l|
=
kt
и
теорема
дает
dKz
_\.
-L.
dr
кР
mz
€f)
илrи
dK
z
dr
(9)
Умножая обе
части
этого
уравнения
kt2
Kz=
-
+
Сr.
2
Для
рассматриваемой
механической
системы
Kz=KY*KP,
Ку
=
Izцs,
где
+
(2D'=
?
и,р
гче ,К7Ш
"
K
rD
-
кинетические
моменты относителъно оси
z
IUIиты
и гру-
эа
D
соответственно.
Поскольку плита вращается
вокруг
осн
z,
то
mУС=
miС=
lпt2\
mrltcos
(
u
J
,
rzz,Icos(
+
)+
+
m,lt'sin
(+)
Для
определения
К
Р
рассмотрим
движение
груза
как
сложное,
считая
его
дDнжение
по
отношению к
плите относительным, 8
вращение
плнты вокруг
оси
z
переносным
движением.
Тогда iD
=
Ъrп
+
Бпер
и, по теореме Варинъона,
(l3)
(
14)Подставив это
значение
mу
с
в
pt}BeHcTBo
(9)
,
найдем
зависимостъ
Лf
от t
u изнее,
полагщ
t=tr=2c,
определим искомую величину
Ц.
Ответ:
Л/l
=
197,3н.
4. О*ределение
угловой
скорости
rлl.
Плита
вращается
вокруг
оси
z,
лежаII1ей
в гtлlоскости
IIлиты
(рис.
Д2в),
и в
момент времени
f
о
=
0,
ког-
да
угловаJI
скоростъ плиты
равна
(rо,
на нее
начинает
действоватъ
врацвю-
цшй мом ент М.
42
Но
вектор Бо* лежит
в ошlоЦ
плоскости с
осью
z
и,
следователъно,
m7
(mrЕотн)
=
0.
Вектор
Тпер
направлен
перпенд{кулярно плите
(как
осъ
х, если
ось
у
в
плоскtrстн плrгы);
по модулю
urr.p
=
cl,
DDr.
Тогда
mz
(mrБп*р)
=
m:
uпер
.
DD,
=
п
za
(DD,
)'.
Но
из
ршс.
Д2в
вишIо, что
DD,
=
I + I
sin
9.
I}зяв
значение
sin
9
из
формулы
(3)
и
подставив все
най-
денные
величины
в
равенство
(
14),
полуrмм
1иrЕ9lц)
*иz
1иrТцgр).
43

КР-m2Ф(DDr)2=m2Фl2
(,-,",#)'
(15
)
из
равенства
(12)
Зная K2n
"
КР
[формулы
(13)
значение
Kz;
тогда
уравнение
1t
1)
пр
tl
m|
**,\
1+cos
+)
']
;""u,"""*,::ou*
(
r
-..,
Т)'
]-
_5t2
* с,.
+
ш,I,
+
m,4l,)
-,
,
Kz,=
(
?
ffi,р
находится
из
равенства
К
z t
=
К
z о.
и
(15)],
имет
вид
12 c"l
-
k"
,,
э
найдем
+ Сr,
или
при числовых
h.rc.
Д3.0
Рис.
Л3.2
Рис.
Л3.4
Рис.
Д3.6
Рис.
Д3.1
Рlас.
Д3.3
Prrc.
Д3.э
0,64
Постоянную интегрирования
определим
по началъным
условиям:
ПРИ |
-
0
(n
=
Ф0
=
5
с-';
получим
С,
-]
128. при
этом
значении
с, из
уравнения
(16)
находим
искомую
зависимость
и.l
от
/.
о т в
е
т:
[,u
-
u
(16)
128 + 5r2
0,64
[ro
*
о
(,
-.",
+
)']
Прuмечанuе.
Из
полученного
результата
можно
найти
и
значение
(rt
при
t
=
tr.
Но
если
по
условиям
задачи
одновременно М=
0,
то
уравнение
(10)
дает
Kz
=
const,
и
тогда
обы.пtо
проще
не
искать
зависимостъ слr от f
в
общем
виде,
а
сначала
определитъ
положение
Фуза
D
при
f
=
0
(т.е.
угол,ро)
ивычислитъзначениеКzо
при
9=9о
и
Ф=Фо
спомощъюра-
BeI{cTB,
анчцlоrичных
(11)
-
(15)
;
затем
определить
положение
фуза
при
t
=
t,
(угол
9r)
й
тем
же
путем
наЙти
Kzt
при
9=
9,
и
@
=
ut.
Так,врассмотренном
примере
приГ
=0
будетро
=пl2п
DD,
=2l
(РиС
Д2в),априt=tr=2с
будет
9t=_тlб
и
DDr=Il2.
тогда
*rо=(
Значение
(,l
+
m,
';
)
G.,l.
Задача
Д3
Механическая
система
состоит
из
грузов
/ п 2
(коэффициент
трения
грузов
о плоскость
/
-
0,1),
цилиндрического
сплошного однородIого
катка
J
и
ступенчатых
шкивов
4
п 5
с
радиусами
ступеней
Ло
=
0,3
м,
мерно
распределенной
по
его
внешнему ободу)
(рис.
Д3.0
-Д3.9,
табл.
Д3).
Тела
системы
соединены
друг
с
другом
нитями,
намотанными
На
шкивы;
участкLI
нитей
параллелы{ы
соответствующим
плоскостям.
44
h{c.
Д3.7
J
htc.
Д3.8
h{c.
Д3.9
45
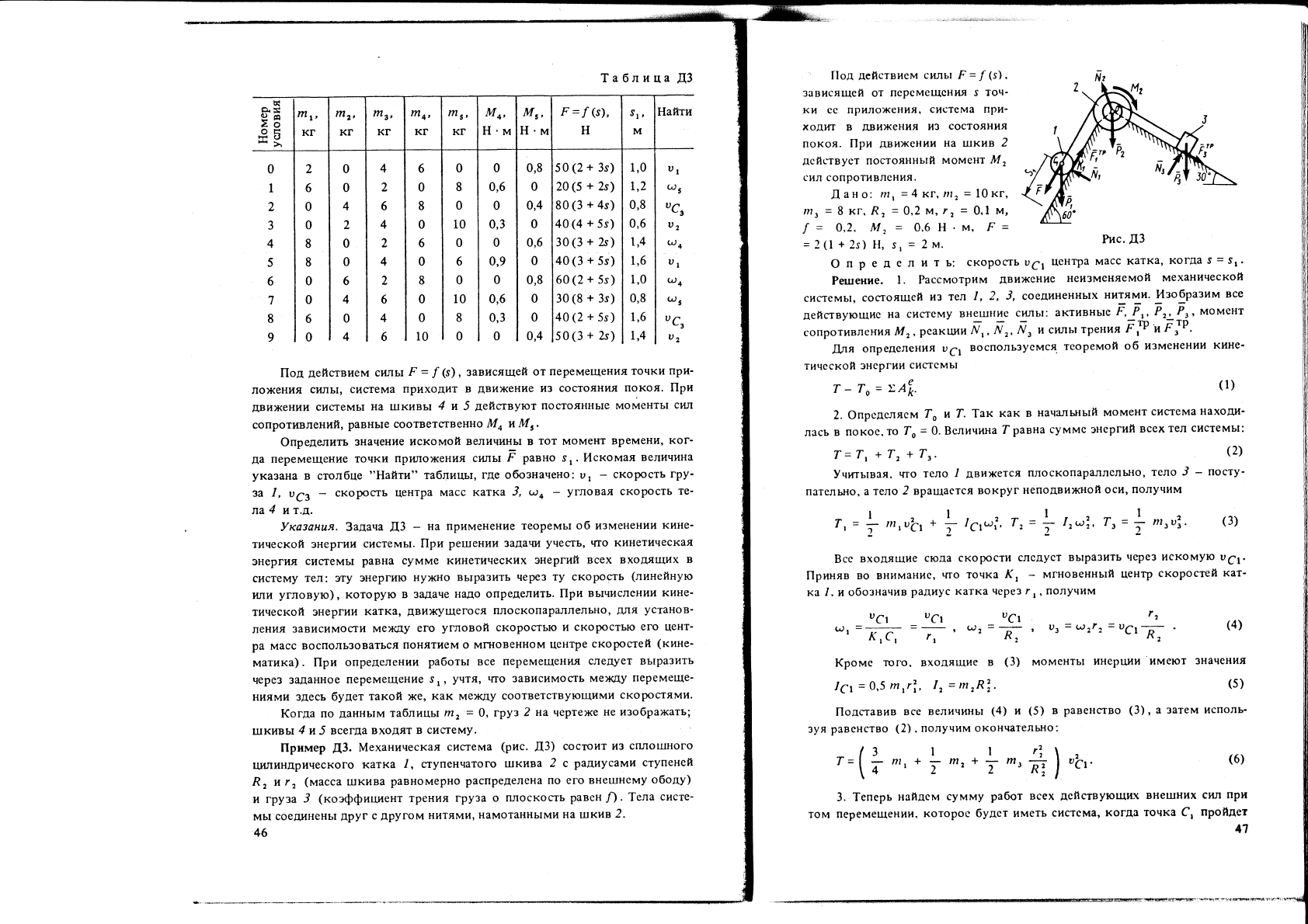
Таблица
Д3
ц
Еý
9я
ао
оtr
Fо
}J.a L
ffi|,
кг
lП2l
кг
Шэ,
кг
Ш4,
кг
Шs,
кг
Мо,
Н,м
Мr,
Н.м
F'
=.f
(s)
н
ýl
,
м
Наltти
0
1
2
3
4
5
6
7
8
9
2
6
0
0
8
8
0
0
6
0
0
0
4
2
0
0
6
4
0
4
4
2
6
4
2
4
2
6
4
6
6
0
8
0
6
0
8
0
0
10
0
8
0
10
0
6
0
10
8
0
0
0,6
0
0,3
0
0,9
0
0,6
0,3
0
0,8
0
0,4
0
0,6
0
0,8
0
0
0,4
50
(2
+
зs)
20
(S
+
2s)
80
(3
+
4s)
40
(4 +
5s)
30
(3
+
2s)
40
(3
+
5;)
60(2
+
5s)
30
(8
+
зs)
40
(2
+
5s)
50(3
+
2s)
1,0
t,2
0,8
0,6
|,4
1,6
1,0
0,8
1,6
L,4
Ur
('ý
uC.
v2
ц)4
U1
u)4
ц)5
uC..,
u2
Под
действием
сильl
F
=
/(s),
зависящей
от
перемещения
точки
при-
ложения
силы,
система
приходит
в
движение
и3 состоянILЕ
покоЯ. ПрИ
движении
системы
на
шкивы
4
и
5
действуют
постоянные
моменты
си.л
сопротивлений,
равные
соответственно
Мо и
М
r.
Опрепелитъ
значение
искомой
величины в
тот
момент
времени,
коГ-
да
перемещение
точки
припожения
сlапы
F
равно
sr. Искомая
ВелИчиНа
указана
в
столбце
"Найти"
таблицы,
где обозначено:
ul
скоростЪ
ГрУ,
за
1,
uСз
скоростъ
центра
масс
катка
3,
l.^)4
угловая
скорость
те-
ла
4
и
т.д.
указанuя.
Задача
Д3
на применение
теоремы
об
изменении
кине,
тической энергии
системы.
При
решении
задачи
учесть,
что
кинетическая
энергия
системы
равна
сумме кинетических
энергиЙ
Всех
в хоДЯЩИХ
В
систему
тел: эту
энергию
нужно
выразитъ
через
ту
скорость
(лиНеЙную
или
угловую),
которую
в задаче
надо
определитъ.
При
вычислении
кине,
тической
энергии
катка,
движущегося
плоскопарiшлельно,
Для
установ-
ления
зависимости
между
его
угловой
скоростъю
и скорстъю
его
цеНТ-
ра
масс
воспользоваться
понятием о мгтIовенном
центре
скоростеЙ
(киНе,
матика)
.
При
определении
работы
все
перемещения
следует
выразить
через заданное
перемещени€
ýr,
учтя,
что
зависимость
между
перемеще-
ниями здесъ будет
такой же,
как
между
соответствующими
скоростями.
Когда
по
данным
таблицы
m
2
=
0,
груз
2 на
чертеже
не изображать;
шкивы
4
п
5
всегда
входят
в
систему.
Пршмер
Д3.
Механическая
система
(рис.
Д3)
состOит
иЗ
сплошного
ципиндрического
катка
l
,
ступенчатого
шкива
2
с
радиусами
стуПеНей
R2
и
г
z
(масса
шкива
равномерно
распределена
по его
внешнемУ
ободУ)
и
груза
3
(коэффициент трения
груза
о
плоскость
равен
/).
Тела
Систе-
MbI
соединены
друг
с
ДрУгом
нитями,
намотанными
на шкив
2.
46
Под
действием
сl,t.пы F'-
/
(s),
зависящей
от
перемещения
ý точ-
к
и
се приложения,
система при-
ходит
в
Ilвижения
из
состояния
покоя.
При
движении
на шкив
2
дсйствует
постоянньlй
момент
М,
сил
сопротивления.
[аНо:
m|
=4кг,
lll2= l0кг,
mз
=
8
кг,
R,
=
0,2
м, r,
=
0,1
м,
f
=
0,2.
М2
=
0,6
н
,м,
F
=
=2(1
+2s)FI,
ýl=2M.
о
п
р
е
д
е Л
и
т ь:
cKopOCTbu6,1 центра
масс
катка,
когдаý=ýt.
решение.
1.
Рассмотрим
движение
неизменяемой
механической
систеМы,
состоящей
из
тел
I, 2,
3,
соединенных
ниаяYИ.
ИзОбразим
все
пействуюшие
на
систему
внешlIие
силы:
активные
F,
Р
r,
Pr--il
,
момент
сопротивления
M,peaкtцtи
N,
,
Nr,
ff,
и силы
трения
FР и
F;п,
Ilля
определения
uct
воспользуемся.
теоремой
об
изменении
кине,
тической
энергии
систсмы
Т
-
То
=
2деk.
2. ОпредеJIяем
То п
Т. Так
как
в
начаJIьныЙ
моменТ
система
находи,
лась
в
покое,
то
Го -
0. Величина
г
равна
сумме энергий
всех
тел
системы:
(t)
Т
=
Т,
+
Т,
*
Т,
Учrгывая.
что
тело
t
движется
плоскопарщIлелыtо,
тело
J
патель}lо, а
тело
2
вращается
вокруг
неподвижной
оси,
получим
Ir-1,
mrv|,
(2)
-
посту-
(3)
l
Т|=т
lll,u},
+
i
ICr-|,
Т2=
l
Тr=Т
l
т
все
входящие
сюда скорсти
следует
выразить
tlерез
искомую
uct.
Приняв
во внимание,
что
точка к,
мгновенный
ЦеНтр
скоростей
кат-
ка
/.
и обозначив
радиус
катка
через r
l
,
получим
uСt
uСt
r
2
=-,
(r,
=-г
,
Uз
=(r2Гz=rс:-
r|
.
=ФzГz
=uСt
&
(4)
кро
ме
ю
го.
входящие
в
(
3)
моменты
инерции
имеют
значения
I
Ct
=
0,5
rп
,
r],
12
=
m
,R|.
(5)
Подставив
все величины
(4)
и
(5)
в
равенство
(3),
а затем
исПоЛЬ-
зуя
равенство
(2).
получим
окончательно:
и)t
3
пl .
+
4l
3.
Теперь
найдем
сумму
работ
всех
деtlствующих
вНешНИх
том
перемешении.
которое бупет
иметь
система,
когда
тОчка Cl
r=
(
l
t
r|
\ о
тmz+тmэtrlОСr.
(б)
сшл
при
пройпет
41
'F,о
'р,
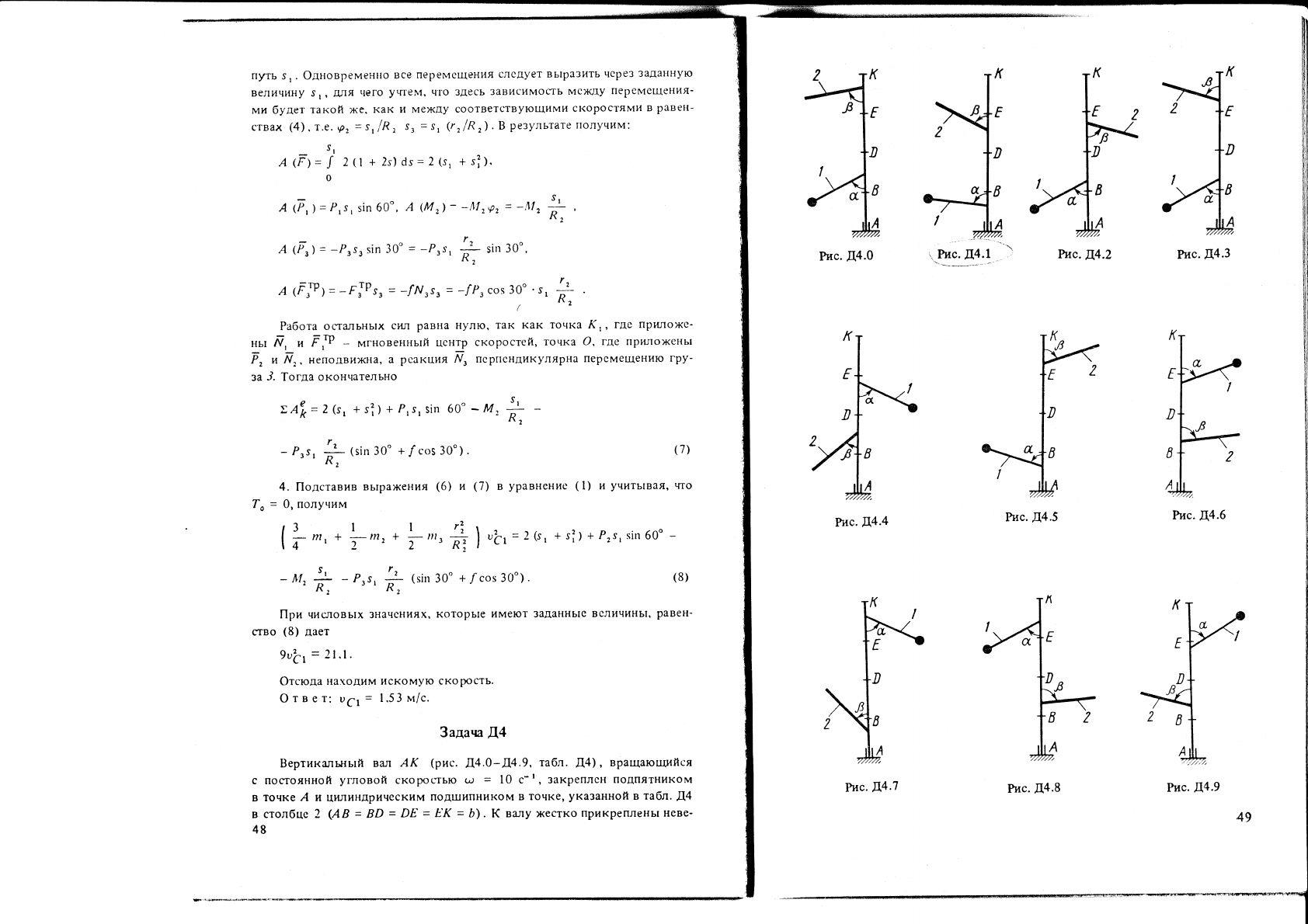
путь
s,
.
ОдновременtIо
все
перемещения
следует
вьIразить через
зада}Iную
веJIИчинУ
s
l,
дIлЯ
чегО
У.ггем,
ч,гО
здесЬ
зависиМостЬ
мсждУ
перемещения_
ми будет
такой же.
как
и между
соответствующими
скоростями
в
равен-
ствах
(4).
т.0.
.pz
=
s,
/Rr
ýз
=
st
qrrlRr).
В
результате
получим:
sl
д(F)=J
2
(l
+ 2s) ds=2
(sr
+ s]).
Д
(Р,
)
=
Prs,
sin
60",
А
(Мr)
-
-trI
,9,
-
-ЛI
,
st
R2
4.
Подставив
выражения
(6)
и
(
7)
в
уравнение
(
1)
То
=
0, получим
А
t&
l
-
-Рэs,
sin
30"
=
-Pus,
Zд'k=2(s,
+ý1
)+P,s,sin
60"-
-
Рrý,
+(sirr
30О
+
/cos
30')
.
t3
l
т
*, +
-лt,*
-p,s,
Г
'-
sirr
30о
R2
Рllc.
Д4.0
Pilc.
Д4.4
hас.
Д4.2
-f
Р, cos 30"
r
Работа
остаJIьных
сиJI
равна
нулю,
так
как
точка К,
,
гДе
Пр}шожс-
HbI
Л,
и
FР
мгновенньlй
цснтр
скоростей,
точка
О, где приложены
F, и
Nr,
неподвижна,
а
реакция
N, перrIсндикулярна
перемещению
грУ-
за
3.
Тогда
окончательно
r2
.с
'
R,
s.
м,
l
-
R2
(7)
и
учитъtвая,
что
l
-m1
),
Ir
+
-
lll,
Ё
)
"Ь,
=
2
(s,
*
ýil
*
Prs, sirt
60"
Э
(sill
30'
+
l'cos
30")
.
(8)
R2
Plrc.
Д4.5
При чисlIовых
значеtlиях,
которые
имеют заданньIе
величины,
равен-
ство
(8)
дает
gub,
=
2I
.l
.
Отсюда
находим
искомую скорсть.
О
т в
е
т:
u6l
=
1.53
pr/c.
Задача
Д4
Вертикапшый
ваJI
АК
(рис.
Д4.0-Д4.9,
табл.
Д4),
вращающийся
с постоянной
угловой
скоростью
ц)
=
10 с-
l,
закреплен
подпятником
в
точке
/
и
цклиндрическим
подшипником
в
точке,
указанной
в
табл.
Л4
в
столбце 2
(ДВ
=
BD
=
DE
=
L'К
=
Ь). К
валrу жестко
прикреплены
неве-
48
Рис.
л4.9
Рис.
Д4.'|
Рлrс.
Д4.8
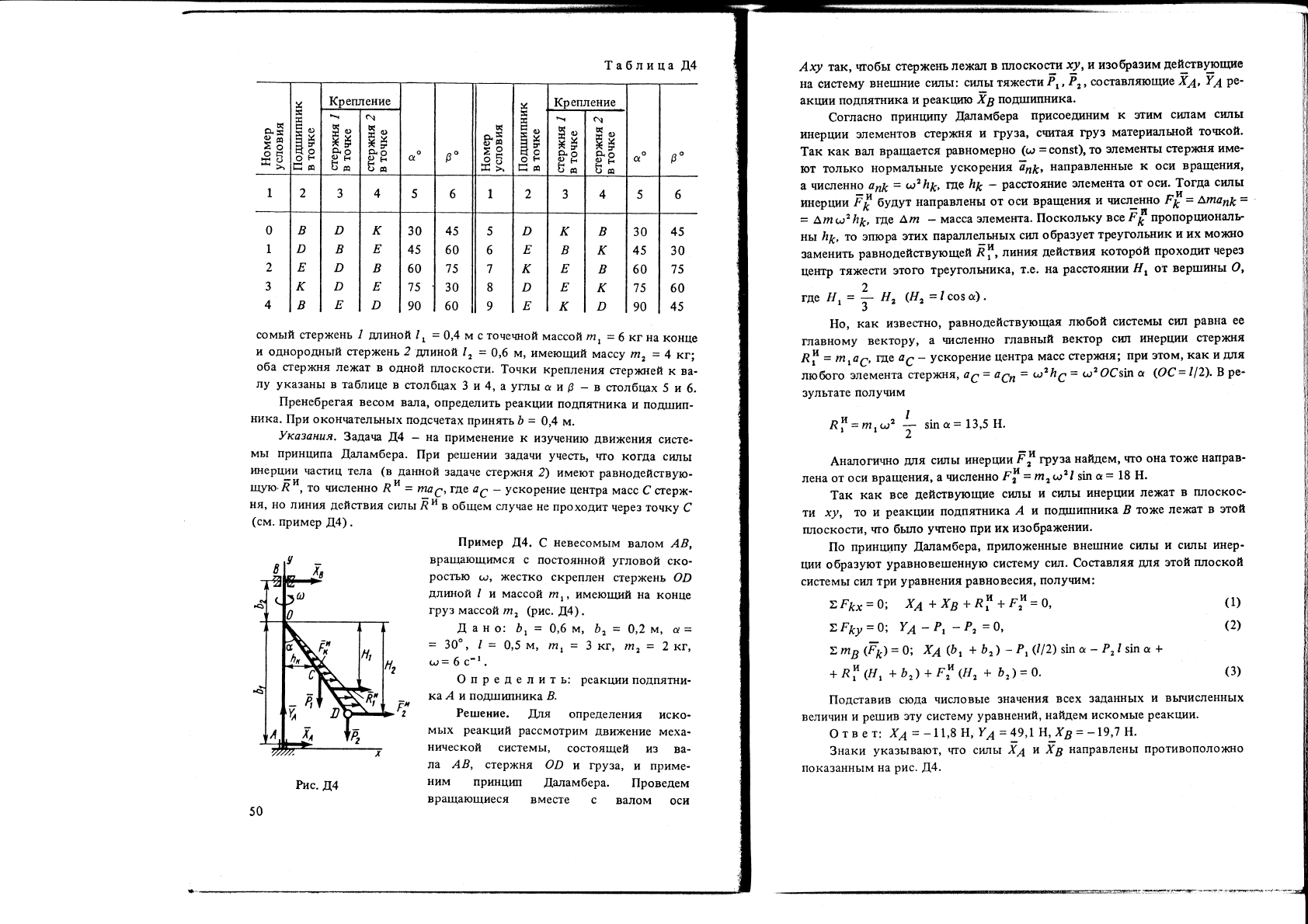
к
ý.ý
gm
ао
он
"Ёо
х
Ё.
tsо>
Ёч
Edo
он
t_; Е
Крепление
о
@
р"
Е
Ыm
Е9
8i
х
5or
Ёх
цс
оF
Еm
Крепление
о
е
р"
5,
хý
fr8
Dрq
С\
5o,
хr
fr8
ts
оФ
5o,
хЕ
ff8
Llm
ýl
5,
хý
frs
tJФ
1
2
J
4
5
6 1
2
3
4
5 6
0
1
2
3
4
в
D
Е
к
в
D
в
D
D
Е
к
Е
в
Е
D
30
45
60
"l5
90
45
60
75
30
60
5
6
1
8
9
D
Е
к
D
Е
к
в
Е
Е
к
в
к
в
к
D
30
45
60
75
90
45
30
75
60
45
Табпица
Д4
сомыЙ
стерженъ
/
длlиной
'1
=
0,4
м с
тоЧечной
массой m|
=
б
кг
на
конце
и
однородный стержень
2
,мUной
12
=
0,6
м, имеющиЙ
массУ m2
=
4 кгi
оба
стержня
лежат
в
одной
плоскости.
Точки
креtшения
стержней
к ва-
лу
указаны
в таблице
в
столбцах
з ц 4,
а
углы
о
и
р
-
в
столбrрх
5 и
6.
пренебрегая
весом
ваJIа,
опредепитъ
реакции
подпятника
и
подшип-
ника.
При
окоЕцlтелы{ых
подсчетах
принять
Ь
=
0,4
м.
УказаНuя.
Задача
д4
на
применение
к
изучению
движения
систе-
мы принципа
Далlамбера.
При
решении
задачи
учесть,
что
когда
сипы
шrерции
частиц
тела
(в
данной
зЕдаче
стержI{
я
2) имеют
равнодействую-
ЩУю,ЛИ,
то
чисJIенно
RИ
=
fllо(lгде
4с
-
ускорение
центра
масс
С стерж-
ня,
но
линия
действия
с}lлы
Е"
"
общем
случае
не
проходит
через
точку
С
(см.
пример
Д4)
.
Пример
Д4.
С
невесомым
ваJIом
АВ,
вращающимся
с
постоянной
угловой
ско-
росТЬЮ
ц),
ЖесТКо
Скреплен
стержеНЬ
OD
длиной
/
и массой
ш
l,
имеющий
на
конце
груз
массой
m,
(рис.
Д4).
ДаНо:
Ь|
=
0,6м, Ь2
=
0,2м, d=
=
30О,
l=
0,5м, lftt=
3кг,
m2=
2кг,
ч.l= б c-l.
о п
р
е
д
е
л
и т ъ:
реакции
подпятни-
каАиподшlшlникаВ.
Решение.
Для
определениlI
иско-
мых
реакций
рассмотрим
движение
меха-
нической
системы,
состоящеfi
из
ва-
ла
АВ,
стержня
OD
и груза,
и приме-
ним
принцип
Даламбера.
Проведем
вращающиеся
вместе
с
валом
оси
дхУ
так, шобы
стФжень
пежап
в
11поскости
х!,и
изофазим
действующие
на
систему
внешние
сипы:
силы
тяжестИРr,
Рr,
составляющие
Хд,
YApe,
акцши подпятника
и
реакцию
7д
подrшипника.
согласно
прин[шпу
!а-rrамбера
присоединим
к
этим
сипам
сипы
инерции
элементов
стержЕя
п
груза,
считая
груз
материапьноЙ
тоtп<оЙ.
Так
как
в:ш
вращается
равномерно
jt*'l
=
const), то
элементы
стержня
име-
ют
толъко
нормilльные
ускорения
апk,
направпенные
К
оси
Вращения,
а
численно
опk
=
сл2 h76,
tде
hk
_
расстояние
элемента
от
оси.
Тогда
сипы
;И
-
,Ё,лЁлrrrlл Еl-Yl
-
Аv*lя
' -
инерIшИ
r
k
будут
направлены
от
оси
вращенпя
и численНо
Fr
-
Ьmап|r=
=
Ь,m
-,
h;,
tде
Аm
-
масса
элемента.
ПосколъкУ
"..
Ff
пропорционtшь
Hbt
hцr,
то
эпюра
этих
парzшлелы{ых
сип образует
треуголъник
и
их
можно
заменитъ
равнодействующей
R
r,
линия
действия
которсiй
проход}tт
чере3
ЦеНТр
тяжести
этого
треугюлы{ика,
т.е.
на
расстоянии
f/,
от
вершины
О,
2
где
Н,
=
т
Н2
(Hz
=
I
cos
о).
но,
как
известно,
равнодействующая
любой
системы
сип
равна
ее
главному
вектору,
а
чисJIенно
главныЙ
вектор
сип
инерции
стержня
Rlп
=
mtaC,
ГДе
ас
-
ускорение
центра
масс
стержня;
при
этом,
как
и
дJIя
любого
элемента
стержня,
ас
=
аСп
=
',)2hC
=
,,l'OCsin
о
(оС
=
Il2).
В
ре-
зулътате
получим
RГ=
Иrа"
+
sina=13,5H,
дналогично
для
сипы
инерци
"
F
У
груза
найдем,
Цо она
тоже
направ,
пена
от
оси
вращения,
ачисленн
о
Fr
=
mr-'J
sin
а
=
18 Н.
Так
как
все
действующие
сипы
и
сшпы
инерции
лежат
в
IIпоскос-
ти
ХУ, то
и
реакщ{и
подпятника
А
и
пошшипника
В
тоже
лежат
в
этоЙ
ппоскости,
чго бьшо
учтено
при их
изображении.
По
принципу
Даламб€рfl,
припоженные
внешние
сипы
ции
образуют
уравновешенную
систему
сип.
Составляя
для
'"*Т;#
;:'
;;
-
;:ffl{
";tr
=ПОЛУЧИМ
:
ЕFky
=0]
Yл-Р,
-Р2
-0,
Еmв
ttrlr)
=
0i
Хд
(Ъ,
*
Ьr)
-
P|(ll2)
sin
а
-
Pzl
sin
е
+
+дIПtн,
*Ьr1 +rf;цн,
+ ьr1=0.
и сипы
инер-
этой плоской
F{
Подставив
сюда
числовые
значения
всех заданных
величин
и
решив
эту систему
уравнений,
найдем искомые
О
т
в
е
т:
Хд=_11,8
Н,,
Yл=49,1
HJrB=
_[9,7
н.
Знаки
указывают,
что
силы
Хд
п Х
в
направпены
показанным
на
рис.
.Щ4.
(1)
(2)
(3)
и
вьнисленных
реакции.
противоположно
50
fu,,д4
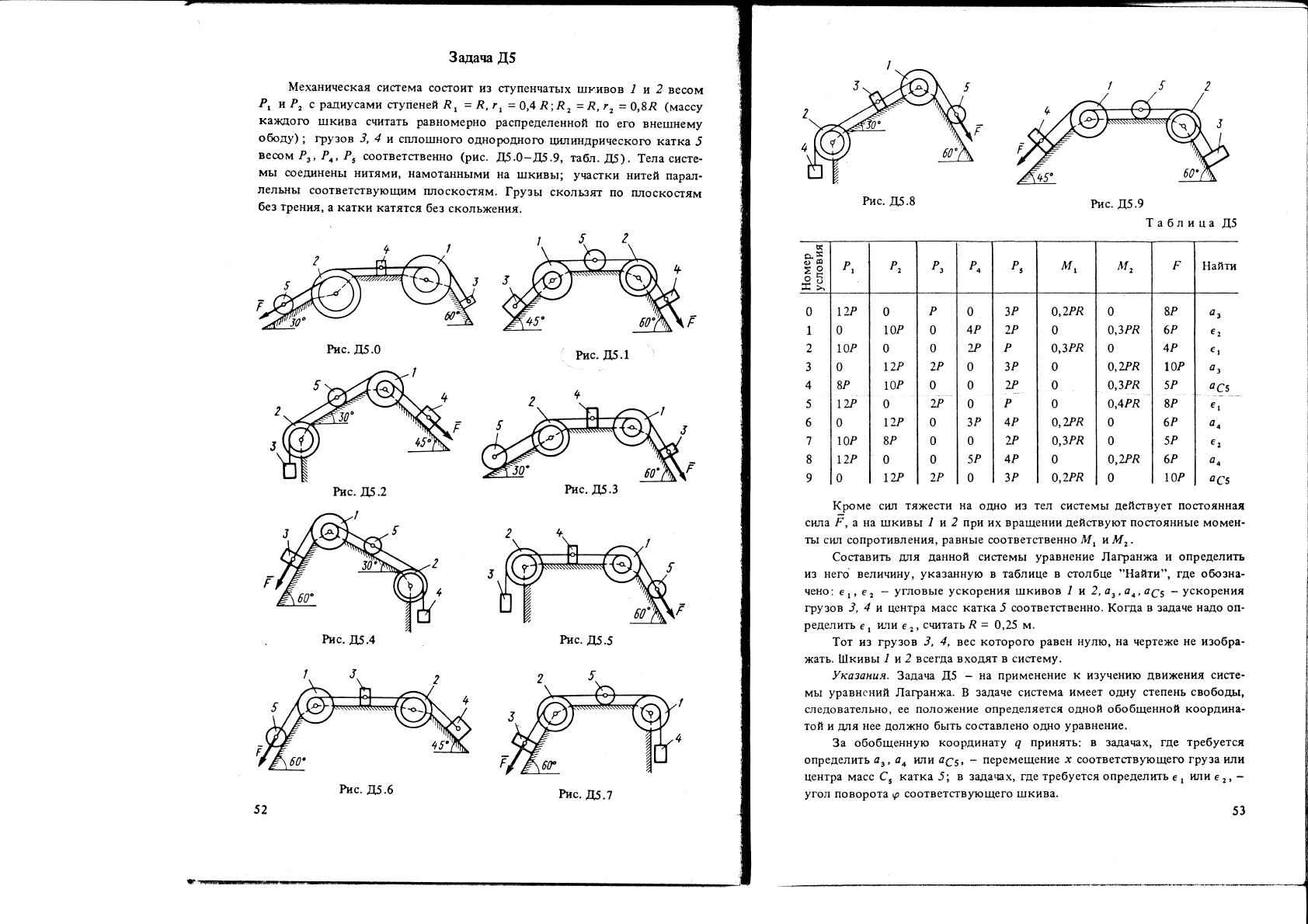
Задача
Д5
Механшческая
система
состошт
из ступенчатых
шr.ивов
I
и
2
весом
Р|
Н
Р,
с
радиусами
ступеней R,
=
R,
/r
=
0,4
R;Rz
=Л,
|z
=
0,8Д
(массу
ках(дого
шкива
считать
равномерно
распределенноft
по
его
внешнему
ободу);
грузов 3, 4
п сwtошного
однородногrэ
щ&пиндрическоrrэ
катка
5
веФм
Рэ,
Р4, Р5
соответственно
(рис.
Д5.0-Д5
.9,
табл.
JIS
)
.
Тела
систе-
мы
соединены
нитями,
намотанными
на шкивы;
участки
нитей
парал-
лельны
соответствующим
плоскостям.
Грузы
скользят
по IUIоскостям
без
трения,
а
катки
катятся
без
скольжения.
hrc.
JIs.0
Рис.
Jý.1
Pllc.
Д5.5
Рис.
Д5.8
Рис.
Д5.9
Таблица
Д5
ц
вý
Е9
fi
р|
р2 рэ р4
р5
м|
м2
F
Найти
0
1
2
3
4
5
6
7
8
9
L2P
0
10р
0
8р
IzP
0
10р
|2р
0
0
10р
0
|2р
10р
0
t2P
8р
0
LzP
р
0
0
2р
0
ф
0
0
0
2р
0
4р
2р
0
0
0
зр
0
5р
0
зр
2р
р
зр
zP
р
4р
zP
4р
зр
0,2рR
0
0,3рд
0
0
0
0,2рR
0,3рл
0
0,2рR
0
0,3рR
0
0,2рR
0,3рR
0,4рR
0
0
0,zPR
0
8р
бр
4р
10р
5р
вр
бр
5р
бр
10р
аэ
е2
€t
аэ
o.9-s
el
а4
е2
а4
aCs
Кроме сшл
тяжести
на
одно
из
тел
системы
действует
постоянная
сипа
F,
а
на
шкивы
/
п
2
прп
их
вращении
действуют
постоянные
момен-
ты сил
сопротивлекия,
равные
соответственно
М,
и Мr.
Составить
дJIя
данной
системы
уравнение
Лагранжа
и определитъ
из него
величину,
указанную
в
таблице в столбце
"Найти",
где обозна-
ченоi
€
1l
€2
угловые
ускорения
шкивов
-I
н
2,
аэ,
а4, oCS
-
ускорения
грузов 3,
4
и
центра
масс
катка
5
соответственно.
Когда
в задаче
надо
оп-
ределитъ
€,
I&r,Iи
€
?,
считатъ
R
=
0,Б м.
Тот из
грузов
3,4,
вес
которого
равен
нулю, н&
чертеже
не изобра-
жатъ.
Шкивы
I
u
2 всегда входят в систему.
указанчя.
Задача
Дs
на применение
к
изучению
движения
систе-
мы
уравнсниfi
Лагранжа.
В задаче
система
имеет одну степень
свободы,
следовательно, ее
положение определяется одной обобщенноfi
коордкна-
той и
для
нее
должно
бытъ
составлено одно
уравнение.
3а
обобщенную
координату
q
принятъ: в задачах, гд9
требуется
ОПРеДеЛИТЬ
аэ, О4
ИПИ
ОС5,
-
ПеРеМеЩеНИе
Х
СООТВеТСТВУЮЩеrý
ГРУЗа ИЛИ
центра
масс
С, катка 5;
в задачах, где
требуется опред9л!{тъ
е,
или
€
2,
-
УГоЛ
ПоВороТа
9
СооТВеТСТВУЮЩеГо
ШКиВа.
53
]
r
r
]
]
l
I
l
I
I
l
*-]
htc.
Ж.2
Plrc.
II5.3
hrc.
JIs.4
52
Pltc.
Д5.6
PIrc.
Ж.'|

Для
составления
уравнения
вычислитъ
сначала
кинетическую
энер_
rИЮ
Т
системы
(как
в
задаче
Д3)
и
выразить
все воrцедIJие
в Г
ско_
рОсТи
через
обобщенную
скоростъ,
т.е.
через
i,
если обобщенная
коорди-
НаТа Х,
uлп через
;,
если
обобщенная координата
9.
Затем вычисJIитъ
Обобщенную
силу
О.
Для
этого
сообщить
системе
возможное
(Maлroe)
перемещение,
при котором
выфанная
координата,
т.е. .r
(илlи
9)
,
полу_
ЧlеТ ПоложIпФIъное
приращение
бх
(или
б
9)
,
и вычислитъ
сумму
элемен_
ТарНых
работ
всех
си.л на
этом перемещении;
в полученном
равенстве
надо
все
другие
тIементарные
перемещения
выразитъ
через бх
(или
че_
рез
б
9,
если
обобщенная координата
g)
и
вынести бх
(или
69)
за скобки.
КоэффиIцtент
при &х
(илlи
б
р)
ч
будет обобщенной
силlой
а
(см.
еще
пример
Д5)
.
Пршмер
Д5.
Механическая система состоит
из ступенчатого шки-
ва
2
(радиусы
ступеней
Д,
и
f
z),
груза
/
и
сплошного
катка J,
прикреп-
ленных
к
концам
нитей,
намотанных
на
ступени
шкива
(рис.
Д5).
На
шкив при еrrэ
вращении
действует
момент с}lп сопротивления М2. Массу
шкива считать
равномерно распределенной
по
внешнему
ободу.
Рис.
Д5
о
=
30".
О
п
р
едел
и
т
ь:
а|
-
ускорение
груза
/.
Решение.
1.
Система
имеет
ошIу
с,тепень свободы.
Выберсм
в ка-
честве
обобщенной
координаты перемещение
х
груза
l
(q
=
х),
полагая,
что
груз
движется
вниз, и,
отсчитывая
х
в сторону
движсния.
Сос,I,ави
м
уравнение
Лагранжа
d t
dТ
t
dГ
гt
тт
l
-
о-
=
а,
2.
Опрепелим
кинетичсскую
энергию
энергий
всех
тел:
Т
=
Т,
*
Т,
+ Тэ.
54
Так
как груз
I
движется
поступателшIо,
шкив 2 вращается
вокруг
неподвижной оси,
а
каток J
движется
плоскопараллелъно,
то
,т|
Рr-
ur,,, Тr,
=
i
Ir-1,
т,
=
+
чЪэ +
У
Ic,
-з,
(з)
I.
L
')о
L6.
где, посколъку
масса
шкива
считается
распределенной
по внешнему
ободу, а
каток
-
сплошной
(его
радиус
обозначим
r
g),
Ir=L
Rr,
Iсз=|
?
|r,.
т=*
{л,
*р,+
|1,7L
*r.
(6)
илп Т=
ц
(4)
3.
Все
скорости,
входящие
в
Г,
,
Т, и Гr,
выразим
через
обобщенную
скоростъ
;,
равную
очевидно,
ur. Еспи
при
этом
учестъ,
что ul
=
.д)rR,
а
uсз
=
Qz|z
и
что
точка
К является
дJIя
катка
J
мrновенным
центром
скоростей, то получим:
'
.,--u'
=i
ro
о
ul
-Х,
l
.
R R
,
uсз-QJrrr=t
Х,
uСз
UСэ
12
.
u)о
=_
=-
-
-=
х.
(5)
'
КСз
rз
rзД
Подставляя
значения
величин
(5)
п
(4)
в
равенства
(3)
,
а
затем
значения
Тr, Т2,
Тэ
в
равенство
(2),
найдем
окончательно,
что
i+рз)
;,
Так
0т
ý
как
здесь Г
зависит
только
от
*,
то
P.oTd
=l1r7-
х,
-
=ý
п
--'
g
0х
dr
I0T
lai
rP..
|
=
11,7
i
х.
(7)
4.
Найдем обобщенную
сшlу
О.Jlпя
этого изобразим силы,
сов€р-
шающие
при
движении
системы
работу,
т.е.
.илlы F, F,
п моме}п
сиJI
сопротивления
Мr,
н'аправленный
против
вращения
шкива.
Затем
сооФ
Iц}tм
системе
возможное
перемещение,
при котором
обобщенная коор-
дината
х
получает положительное
приращение
бх,
и покажем
перемеще-
ния
каждого из
тел;
IШя
груза
/
это будет
бs,
=
бх,
дJIя
шкива
2
-
пово,
рот
на
уг!л
69z,
мя
катка З
-
перемещение
бs,
его
цента.
После
этого
вычислим сумму
элементарных
работ
сил и
момента
на
данных
пере-
мещениях.
ПолуtЕtм
бд
=
Pr 6s,
-
IW169,
-
Рэ
sin
о6ýr.
Все
входящие
сюда псремещения
надо
выразить через
бх.
Утгя,
tlTo
зависимости
между
uIементарными
перемещениями
здесь
аналогичны
зависимостям
(5)
между
соответствующими
скоростями,
получим
(8)
(l)
Т
сиL-тсмьl,
равную
сумме
(2)
бх
6ý,
=
бХ,
Вр,
=
т
6ýr=trБ9r=+6х.
д
(9)
55
"I
Подставляя
эти значения
в
равенство
(в)
и въшося
бх
за скобки,
найдем,
шо
бл=
(r,
-
+
-
?
р,
sinc
)u".
(10)
коэффициент
при
бх
в
полученном
выражении
и
будет обобщенной
срtлtой
Q.
Спеповательно,
о=р.
М2
-р^.Г,
^:-^,
<,l
_l
R "ЁsiпсиflиQ=4,3Р.
(11)
5. Подставляя
найденные
величины
(7)
и
(
1 1)
в
уравнение
(
1)
,
получим
Р
..
11,7
-
х=4,3Р.
g
отсюда
находим
искомое
ускоре
ние
а,
=
х.
ОТвет:
а|
=0,37g.
Прuмечанuе.
Если в ответе
получится
а
{
0
(шпи
е
<
0), то
это
озна_
чает,
что система
движется
не
в ту
сторону,
куда
было предположено.
тогда
У
момента
Мr,
направленного
против
вращения
шкива,
изменится
направЛение
и,
слеДовательно,
каК видно
из
равенства
(11),
изменится
величина
Q,
для
которой
надо
найти
новое
верное
значение.
Задача
Д6*
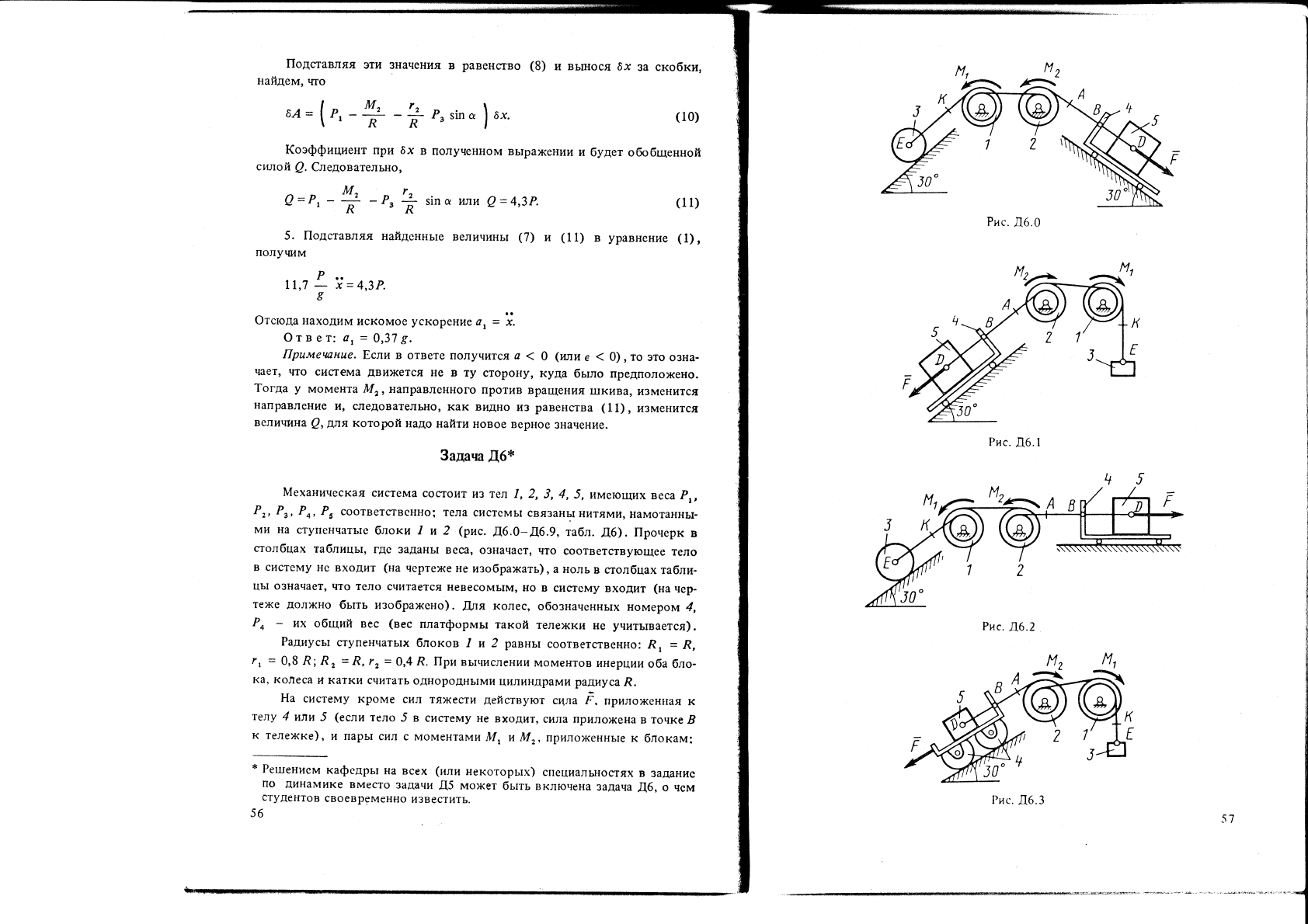
Механическая
система
состоит
из
тел
I,2,3,4,
J,
имеющих
веса
Рr,
Р2,
Рэ,
Р4,
Pg
СООТВеТСТВеННО;
ТеЛа
СИСТеМЫ
СВЯЗаНЫ
НИТЯМИ,
НаМОТаННЫ-
ми
на
ступенчатые
блоки
I
и 2
(рис.
д6.0*д6.9,
табл.
д6).
Прочерк
в
сголбцах
таблицы,
где заданы
веса,
означает,
что
соответствующее
тело
в систему
не
входит
(на
чертеже
не
изображатъ),
а
ноль
в
столбцах
табли-
цы
означает,
что тело
считается
невесомыМ,
но
в
систему
входит
(на
чер-
теже
должно
быть изображено).
Для
колес,
обозначенных
номером
4,
р4
иХ
общий
веС
(вес
платформы
такой
тележки
не
учитывается).
Радиусы
ступенчатых
блоков
I
и 2
равны
соответственно:
R,
-
R,
r|
=
0,8
R;
R,
=
R,
Iz
=
0,4
R. При
вычислении
моментов
инерции
оба
бло-
ка,
Колеса
и каткИ считатЬ
однорОднымИ
цилиндрами
рапиуса
R.
На
системУ
кроме
сил тяжести
действуют
сцла
F.
приложенtIая
к
телу
4
uлп
5
(если
тело
5
в
систему
не
входит,
сила приложена
в точке
В
К
тележке),
и
пары сил
с
моментами
М,
И Мr,
приложенные
к
блокам:
*
Решением
кафепры
на
всех
(или
неко.горых)
сrrециалъностях
по
динамике
вместо
задачи
Д5
может
быть
включена
задача
студентов
своевременно
известить.
56
в
задание
Д6,
о чем
]
l
1
l
}
t
l
I
Рис.
л6.0
Рис.
Д6.I
Рис.
Д6.2
57
4
l
[)и с.
л6.
3
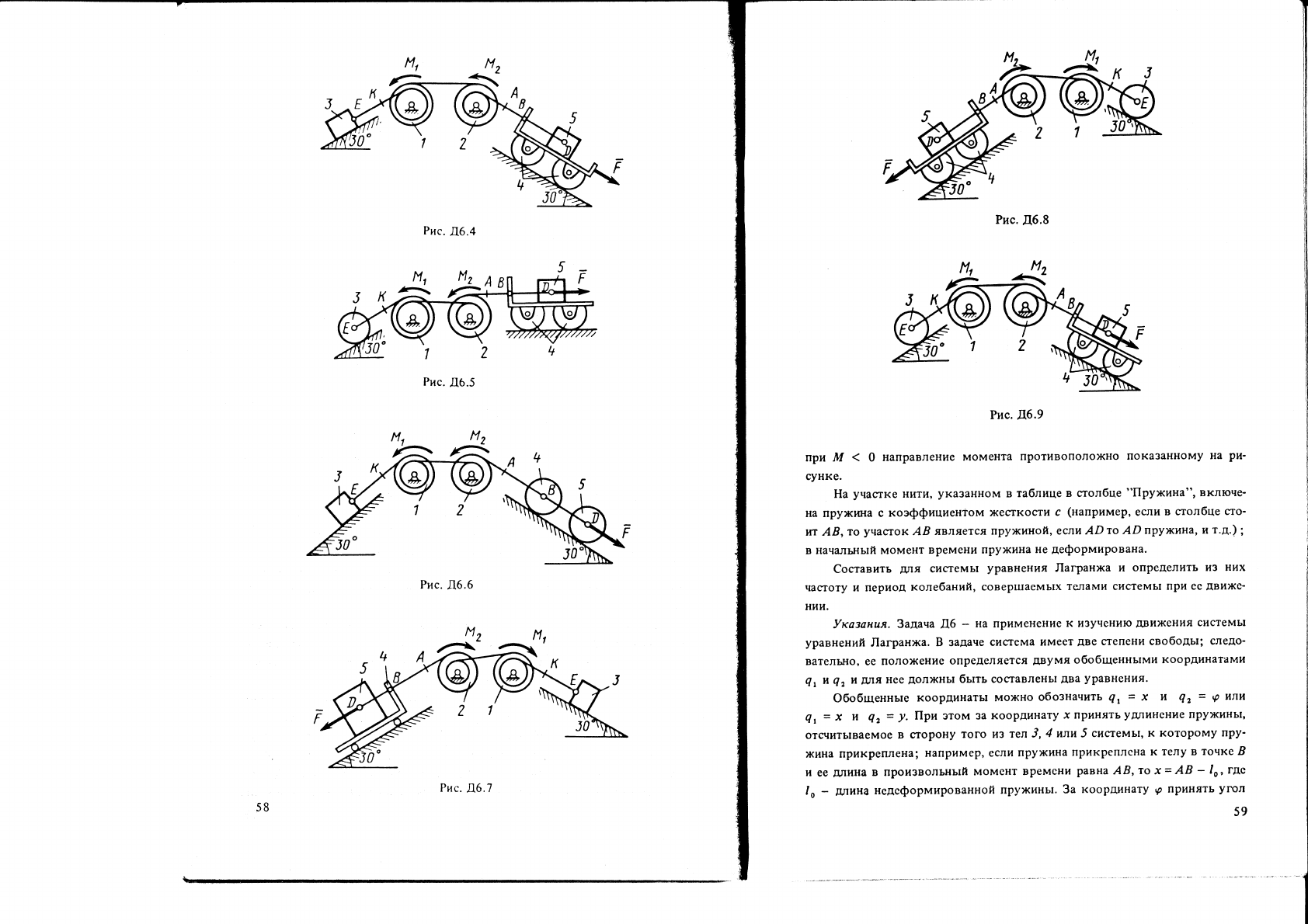
Рис.
Д6.4
Рис.
л6.6
м1
.a!Ё\
Рис.
Д6.8
Рис.
Д6.9
сунке.
На
участке
нити,
указанном
в
таблице
в
столбце
"Пружинд",
вклюЧе-
на пружина
с коэффициентом
жесткости
с
(например,
если
в столбце
сто,
чт АВ,
то
участок
АВ
является
пружиной,
если
ADTo
АDпружина,
и
Т.д.);
в начiulьный момент
времени
пружина
не
пеформирована.
Составить
длIя
системы
уравнения
Лагранжа
и
определитъ
иЗ
них
частоту
и период
колебаний,
совершаемых
теJIами
системы
при ее
движе-
нии.
Указанuя.
3адача
Дб
-
на
применение
к изучению
движения
системы
уравнений
Лагранх(а.
В задаче
сиfiема
имеет
две
степени
свободы;
слеДо,
вателъно,
ее
положение
определяется
двумя
обобщенными
координатами
Q
t
И
Q
z
и
дrtя
нее
Должны
быть
составлены
два
уравнения.
Обобщенные
координаты
можно
обозначитъ
Qt
=
х
и
Qz
=
g
ИЛП
Qt
-
х
и
Qz
-
у.
При
этом за
координату
х
принять
удлинение
пружины,
отсчитываемое
в сторону
того из
тел
3,4
или
5
системы,
к котороМУ
ПРУ,
жина прикреплена;
например,
если
пружина
прикреплена
к
телу
в
точке В
и
ее
ддина
в произволъный
момент
времсни
равна
АВ,
то
х
=
ДВ
-
'о,
ГДС
,о
дrIина
непеформированной
пружины.
За
координату
9
ПриНять
угýЛ
58
Ри с.
Д6.
7
59
