Tan S.T. Finite Mathematics for the Managerial, Life, and Social Sciences
Подождите немного. Документ загружается.

This page intentionally left blank

APPENDIX B
THE SYSTEM OF REAL
NUMBERS
87533_10_APP_p537-578 1/30/08 10:27 AM Page 563
In this appendix, we briefly review the system of real numbers. This system consists
of a set of objects called real numbers together with two operations, addition and mul-
tiplication, that enable us to combine two or more real numbers to obtain other real
numbers. These operations are subject to certain rules that we will state after first
recalling the set of real numbers.
The set of real numbers may be constructed from the set of natural (also called
counting) numbers
N {1, 2, 3, . . .}
by adjoining other objects (numbers) to it. Thus, the set
W {0, 1, 2, 3, . . .}
obtained by adjoining the single number 0 to N is called the set of whole numbers.
By adjoining negatives of the numbers 1, 2, 3, . . . to the set W of whole numbers, we
obtain the set of integers
I {. . . , 3, 2, 1, 0, 1, 2, 3, . . .}
Next, consider the set
Q
Now, the set I of integers is contained in the set Q of rational numbers. To see this,
observe that each integer may be written in the form a/b with b 1, thus qualifying
as a member of the set Q. The converse, however, is false, for the rational numbers
(fractions) such as
, , and so on
are clearly not integers.
The sets N, W, I, and Q constructed thus far have the relationship
N 傺 W 傺 I 傺 Q
That is, N is a proper subset of W, W is a proper subset of I, and I is a proper subset
of Q.
Finally, consider the set Ir of all real numbers that cannot be expressed in the form
a/b, where a, b are integers (b 0). The members of this set, called the set of irra-
tional numbers, include , , , and so on. The set
R Q 傼 Ir
which is the set of all rational and irrational numbers, is called the set of all real num-
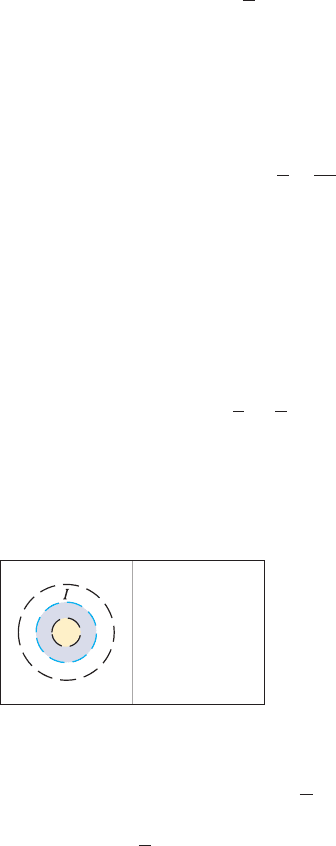
bers (Figure 1).
Note the following important representation of real numbers: Every real number
has a decimal representation; a rational number has a representation as a terminating
or repeating decimal. For example, 0.025, and
0.142857142857142857. . .
Note that the block of
integers 142857 repeats.
1
7
1
40
Q Ir
W
N
Q =
I =
W =
N =
Ir =
Rationals
Integers
Whole numbers
Natural numbers
Irrationals
1312
23
25
1
2
e
a
b
`a and b are integers with b Z 0 f
564 B SYSTEM OF REAL NUMBERS
FIGURE 1
The set of all real numbers consists of
the set of rational numbers and the set of
irrational numbers.
87533_10_APP_p537-578 1/30/08 10:27 AM Page 564

On the other hand, the irrational number has a representation as a nonrepeating
decimal. Thus,
1.41421. . .
As mentioned earlier, any two real numbers may be combined to obtain another
real number. The operation of addition, written , enables us to combine any two
numbers a and b to obtain their sum, denoted by a b. Another operation, called mul-
tiplication, and written
, enables us to combine any two real numbers a and b to form
their product, denoted by a
b, or, more simply, ab. These two operations are sub-
jected to the following rules of operation: Given any three real numbers a, b, and c,
we have
I. Under addition
1. a b b a
Commutative law of addition
2. a (b c) (a b) c Associative law of addition
3. a 0 a Identity law of addition
4. a (a) 0 Inverse law of addition
II. Under multiplication
1. ab ba
Commutative law of multiplication
2. a(bc) (ab)c Associative law of multiplication
3. a
1 a Identity law of multiplication
4. a(1/a) 1(a 0) Inverse law of multiplication
III. Under addition and multiplication
1. a(b c) ab ac
Distributive law for multiplication with respect to
addition
12
12
B THE SYSTEM OF REAL NUMBERS 565
87533_10_APP_p537-578 1/30/08 10:27 AM Page 565
This page intentionally left blank

APPENDIX C
REVIEW OF LOGARITHMS
87533_10_APP_p537-578 1/30/08 10:27 AM Page 567

Logarithms
You are already familiar with exponential equations of the form
b
y
x (b 0, b 1)
where the variable x is expressed in terms of a real number b and a variable y. But what
about solving this same equation for y? You may recall from your study of algebra that
the number y is called the logarithm of x to the base b and is denoted by log
b
x. It is
the power to which the base b must be raised in order to obtain the number x.
Observe that the logarithm log
b
x is defined only for positive values of x.
EXAMPLE 1
a. log
10
100 2 since 100 10
2
b. log
5
125 3 since 125 5
3
c. log
3
3 since 3
3
d. log
20
20 1 since 20 20
1
EXAMPLE 2
Solve each of the following equations for x.
a. log
3
x 4 b. log
16
4 x c. log
x
8 3
Solution
a. By definition, log
3
x 4 implies x 3
4
81.
b. log
16
4 x is equivalent to 4 16
x
(4
2
)
x
4
2x
, or 4
1
4
2x
, from which we
deduce that
2x 1
b
m
b
n
⇒
m
n
x
c. Referring once again to the definition, we see that the equation log
x
8 3 is equiva-
lent to
8 2
3
x
3
x 2
a
m
b
m
⇒
a
b
The two widely used systems of logarithms are the system of common loga-
rithms, which uses the number 10 as the base, and the system of natural logarithms,
which uses the irrational number e 2.71828. . . as the base. Also, it is standard prac-
tice to write log for log
10
and ln for log
e
.
Logarithmic Notation
log x log
10
x Common logarithm
ln x log
e
x Natural logarithm
1
2
1
3
3
1
27
1
27
Logarithm of x to the Base b, b 0, b 1
y log
b
x if and only if x b
y
(x 0)
568 C REVIEW OF LOGARITHMS
87533_10_APP_p537-578 1/30/08 10:27 AM Page 568

The system of natural logarithms is widely used in theoretical work. Using natural
logarithms rather than logarithms to other bases often leads to simpler expressions.
Laws of Logarithms
Computations involving logarithms are facilitated by the following laws of logarithms.
Do not confuse the expression log m/n (Law 2) with the expression log m/log n.
For example,
log log 100 log 10 2 1 1 2
The following examples illustrate the properties of logarithms.
EXAMPLE 3
a. log(2
3) log 2 log 3 b. ln ln 5 ln 3
c. log log 7
1/2
log 7 d. log
5
1 0
e. log
45
45 1
EXAMPLE 4
Given that log 2 0.3010, log 3 0.4771, and log 5 0.6990, use
the laws of logarithms to find
a. log 15 b. log 7.5 c. log 81
Solution
a. Note that 15 3
5, so by Law 1 for logarithms,
log 15 log 3
5
log 3 log 5
0.4771 0.6990
1.1761
b. Observing that 7.5 15/2 (3
5)/2, we apply Laws 1 and 2, obtaining
log 7.5 log
(3)
2
(5)
log 3 log 5 log 2
0.4771 0.6990 0.3010
0.8751
1
2
17
5
3
2
1
log 100
log 10
100
10
Laws of Logarithms
If m and n are positive numbers and b 0, b 1, then
1. log
b
mn log
b
m log
b
n
2. log
b
log
b
m log
b
n
3. log
b
m
r
r log
b
m for any real number r
4. log
b
1 0
5. log
b
b 1
C REVIEW OF LOGARITHMS 569
m
n
87533_10_APP_p537-578 1/30/08 10:27 AM Page 569

c. Since 81 3
4
, we apply Law 3 to obtain
log 81 log 3
4
4 log 3
4(0.4771)
1.9084
Examples 5 and 6 illustrate how the properties of logarithms are used to solve equations.
EXAMPLE 5
Solve log
3
(x 1) log
3
(x 1) 1 for x.
Solution
Using the properties of logarithms, we obtain
log
3
(x 1) log
3
(x 1) 1
log
3
1 Law 2
3
1
3 Definition of logarithms
So,
x 1 3(x 1)
x 1 3x 3
4 2x
x 2
EXAMPLE 6
Solve log x log(2x 1) log 6.
Solution
We have
log x log(2x 1) log 6
log x log(2x 1) log 6 0
log 0
Laws 1 and 2
10
0
1 Definition of logarithms
So,
x(2x 1) 6
2x
2
x 6 0
(2x 3)(x 2) 0
x or 2
Since the domain of log(2x 1) is the interval (because 2x 1 must be posi-1
1
2
, 2
3
2
x12x 12
6
c
x12x 12
6
d
Remember to check to see if the
original equation holds true for
x
2.
x 1
x 1
x 1
x 1
570 C REVIEW OF LOGARITHMS
tive), we reject the root of the quadratic equation and conclude that the solution
of the given equation is x 2.
Note
Using the fact that log a log b if and only if a b, we can also solve the
equation of Example 6 in the following manner:
log x log(2x 1) log 6
log x(2x 1) log 6
x(2x 1) 6
The rest of the solution is the same as that in Example 6.
3
2
87533_10_APP_p537-578 1/30/08 10:27 AM Page 570

In Exercises 15–22, use the laws of logarithms to solve
the equation.
15. log
2
x 3 16. log
2
8 x
17. log
x
10
3
3 18. log
x
2
19. log
2
(2x 5) 3 20. log
4
(5x 4) 2
21. log
5
(2x 1) log
5
(x 2) 1
22. log(x 7) log(x 2) 1
In Exercises 23–30, use logarithms to solve the equation
for t.
23. e
0.4t
8 24. e
3t
0.9
25. 5e
2t
6 26. 4e
t1
4
27. 2e
0.2t
4 6 28. 12 e
0.4t
3
29. 20 30. 100
200
1 3e
0.3t
50
1 4e
0.2t
1
3
1
16
C REVIEW OF LOGARITHMS 571
In Exercises 1–6, express each equation in logarithmic
form.
1. 2
6
64 2. 3
5
243
3. 3
2
4. 5
3
5. 32
3/5
8 6. 81
3/4
27
In Exercises 7–10, use the facts that log 3 ⬇ 0.4771 and
log 4 ⬇ 0.6021 to find the value of each logarithm.
7. log 12 8. log
9. log 16 10. log
In Exercises 11–14, write the expression as the logarithm
of a single quantity.
11. 2 ln a 3 ln b 12. ln x 2 ln y 3 ln z
13. ln 3 ln x ln y ln z
14. ln 2 ln(x 1) 2 ln(1 )1x
1
2
1
3
1
2
1
2
13
3
4
1
125
1
9
Exercises
87533_10_APP_p537-578 1/30/08 10:27 AM Page 571
