Tan S.T. Finite Mathematics for the Managerial, Life, and Social Sciences
Подождите немного. Документ загружается.

522 9 MARKOV CHAINS AND THE THEORY OF GAMES
opponent’s optimal strategy cannot be used to advantage. Such strategies are called
pure strategies. In this section, we look at games that are not strictly determined and
the strategies associated with such games.
Mixed Strategies
As a simple example of a game that is not strictly determined, let’s consider the fol-
lowing slightly modified version of the coin-matching game played by Richie and
Chuck (see Example 1, Section 9.4). Suppose Richie wins $3 if both parties choose
heads and $1 if both choose tails and loses $2 if one chooses heads and the other tails.
Then, the payoff matrix for this game is given by
C ’s moves
C
1
C
2
(heads) (tails)
R’s moves
A quick examination of this matrix reveals that it contains no entry that is simul-
taneously the smallest entry in its row and the largest entry in its column; that is, the
game has no saddle point and is therefore not strictly determined. What strategy might
Richie adopt for the game? Offhand, it would seem that he should consistently select
row 1 since he stands to win $3 by playing this row and only $1 by playing row 2, at
a risk, in either case, of losing $2. However, if Chuck discovers that Richie is playing
row 1 consistently, he would counter this strategy by playing column 2, causing
Richie to lose $2 on each play! In view of this, Richie is led to consider a strategy
whereby he chooses row 1 some of the time and row 2 at other times. A similar analy-
sis of the game from Chuck’s point of view suggests that he might consider choosing
column 1 some of the time and column 2 at other times. Such strategies are called
mixed strategies.
From a practical point of view, there are many ways in which a player may choose
moves in a game with mixed strategies. For example, in the game just mentioned, if
Richie decides to play heads half the time and tails the other half of the time, he could
toss an unbiased coin before each move and let the outcome of the toss determine
which move he should make. Here is another more general but less practical way of
deciding on the choice of a move: Having determined beforehand the proportion of the
time row 1 is to be chosen (and therefore the proportion of the time row 2 is to be cho-
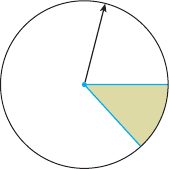
sen), Richie might construct a spinner (Figure 3) in which the areas of the two sectors
reflect these proportions and let the move be decided by the outcome of a spin. These
two methods for determining a player’s move in a game with mixed strategies guaran-
tee that the strategy will not fall into a pattern that will be discovered by the opponent.
From a mathematical point of view, we may describe the mixed strategy of a row
player in terms of a row vector whose dimension coincides with the number of possi-
ble moves the player has. For example, if Richie had decided on a strategy in which
he chose to play row 1 half the time and row 2 the other half of the time, then this strat-
egy is represented by the row vector
[.5 .5]
Similarly, the mixed strategy for a column player may be represented by a column
vector of appropriate dimension. For example, returning to our illustration, suppose
Chuck has decided that 20% of the time he will choose column 1 and 80% of the time
he will choose column 2. This strategy is represented by the column vector
c
.2
.8
d
c
3 2
21
d
R
1
(heads)
R
2
(tails)
T
ails
Heads
FIGURE 3
87533_09_ch9_p483-536 1/30/08 10:12 AM Page 522

Expected Value of a Game
For the purpose of comparing the merits of a player’s different mixed strategies in a
game, it is convenient to introduce a number called the expected value of a game. The
expected value of a game measures the average payoff to the row player when both
players adopt a particular set of mixed strategies. We now explain this notion using a
2 2 matrix game whose payoff matrix has the general form
A
Suppose in repeated plays of the game the row player R adopts the mixed strategy
P [ p
1
p
2
]
(that is, the player selects row 1 with probability p
1
and row 2 with probability p
2
), and
the column player C adopts the mixed strategy
Q
(that is, the column player selects column 1 with probability q
1
and column 2 with
probability q
2
). Now, in each play of the game, there are four possible outcomes that
may be represented by the ordered pairs
(row 1, column 1)
(row 1, column 2)
(row 2, column 1)
(row 2, column 2)
where the first number of each ordered pair represents R’s selection and the second
number of each ordered pair represents C’s selection. Since the choice of moves is
made by one player without knowing the other’s choice, each pair of events (for exam-
ple, the events “row 1” and “column 1”) constitutes a pair of independent events.
Therefore, the probability of R choosing row 1 and C choosing column 1, P(row 1,
column 1), is given by
P(row 1, column 1) P(row 1)
P(column 1)
p
1
q
1
In a similar manner, we compute the probability of each of the other three out-
comes. These calculations, together with the payoffs associated with each of the four
possible outcomes, may be summarized as follows:
Outcome Probability Payoff
(row 1, column 1) p
1
q
1
a
11
(row 1, column 2) p
1
q
2
a
12
(row 2, column 1) p
2
q
1
a
21
(row 2, column 2) p
2
q
2
a
22
Then, the expected payoff E of the game is the sum of the products of the payoffs
and the corresponding probabilities (see Section 8.2). Thus,
E p
1
q
1
a
11
p
1
q
2
a
12
p
2
q
1
a
21
p
2
q
2
a
22
In terms of the matrices P, A, and Q, we have the following relatively simple expres-
sion for E—namely,
E PAQ
c
q
1
q
2
d
c
a
11
a
12
a
21
a
22
d
9.5 GAMES WITH MIXED STRATEGIES 523
87533_09_ch9_p483-536 1/30/08 10:13 AM Page 523

which you may verify (Exercise 22). This result may be generalized as follows:
We now look at several examples involving the computation of the expected
value of a game.
APPLIED EXAMPLE 1
Coin-Matching Game Consider a coin-
matching game played by Richie and Chuck with the payoff matrix (in dol-
lars) given by
A
Compute the expected payoff of the game if Richie adopts the mixed strategy P
and Chuck adopts the mixed strategy Q, where
a. P [.5 .5] and Q
b. P [.8 .2] and Q
Solution
a. We compute
E PAQ [.5 .5]
[.5 .5]
0
c
.5
.5
d
c
3 2
21
d c
.5
.5
d
c
.1
.9
d
c
.5
.5
d
c
3 2
21
d
524 9 MARKOV CHAINS AND THE THEORY OF GAMES
Expected Value of a Game
Let
q
1
q
2
P [ p
1
p
2
. . .
p
m
] and Q
冤
冥
q
n
be the vectors representing the mixed strategies for the row player R and the col-
umn player C, respectively, in a game with the m n payoff matrix
a
11
a
12
. . .
a
1n
a
21
a
22
. . .
a
2n
A
冤
冥
a
m1
a
m2
. . .
a
mn
Then the expected value of the game is given by
a
11
a
12
. . .
a
1n
q
1
a
21
a
22
. . .
a
2n
q
2
E PAQ [p
1
p
2
. . .
p
m
]
冤
冥冤
冥
a
m1
a
m2
. . .
a
mn
q
n
87533_09_ch9_p483-536 1/30/08 10:13 AM Page 524

Thus, in repeated plays of the game, it may be expected that in the long-term,
the payoff to each player is 0.
b. We compute
E PAQ [.8 .2]
[2 1.4]
1.06
That is, in the long run Richie may be expected to lose $1.06 on the average
in each play.
EXAMPLE 2
The payoff matrix for a certain game is given by
A
a. Find the expected payoff to the row player if the row player R uses her maximin
pure strategy and the column player C uses her minimax pure strategy.
b. Find the expected payoff to the row player if R uses her maximin strategy 50%
of the time and chooses each of the other two rows 25% of the time, while C
chooses each column 50% of the time.
Solution
a. The maximin and minimax strategies for the row and column players, respec-
tively, may be found using the method of the last section. Thus,
Row
minima
2
1 씯 Largest of the row minima
3
Column maxima 3 2
앖
Smaller of the column maxima
From these results, we see that R’s optimal pure strategy is to choose row 2,
whereas C’s optimal pure strategy is to choose column 2. Furthermore, if both
players use these strategies, then the expected payoff to R is 2 units.
b. In this case, R’s mixed strategy may be represented by the row vector
P [.25 .50 .25]
and C’s mixed strategy may be represented by the column vector
Q
The expected payoff to the row player will then be given by
E PAQ [.25 .50 .25]
[.5 .25]
.125
c
.5
.5
d
£
1 2
12
3 3
§ c
.5
.5
d
c
.5
.5
d
£
1 2
12
3 3
§
£
1 2
12
3 3
§
c
.1
.9
d
c
3 2
21
d c
.1
.9
d
9.5 GAMES WITH MIXED STRATEGIES 525
87533_09_ch9_p483-536 1/30/08 10:13 AM Page 525

In the last section, we studied optimal strategies associated with strictly deter-
mined games and found them to be precisely the maximin and minimax pure strate-
gies adopted by the row and column players. We now look at optimal mixed strategies
associated with matrix games that are not strictly determined. In particular, we state,
without proof, the optimal mixed strategies to be adopted by the players in a
2 2 matrix game.
As we saw earlier, a player in a nonstrictly determined game should adopt a mixed
strategy since a pure strategy will soon be detected by the opponent, who may then
use this knowledge to his advantage in devising a counterstrategy. Since there are infi-
nitely many mixed strategies for each player in such a game, the question arises as to
how an optimal mixed strategy may be discovered for each player. An optimal mixed
strategy for a player is one in which the row player maximizes his expected payoff and
the column player simultaneously minimizes the row player’s expected payoff.
More precisely, the optimal mixed strategy for the row player is arrived at using
the following argument: The row player anticipates that any mixed strategy he adopts
will be met by a counterstrategy by the column player that will minimize the row
player’s payoff. Consequently, the row player adopts the mixed strategy for which the
expected payoff to the row player (when the column player uses his best counterstrat-
egy) is maximized.
Similarly, the optimal mixed strategy for the column player is arrived at using the
following argument: The column player anticipates that the row player will choose a
counterstrategy that will maximize the row player’s payoff regardless of the mixed
strategy he (the column player) chooses. Consequently, the column player adopts the
mixed strategy for which the expected payoff to the row player (who will use his best
counterstrategy) is minimized.
Without going into details, let’s note that the problem of finding the optimal
mixed strategies for the players in a nonstrictly determined game is equivalent to the
problem of solving a related linear programming problem. However, for a 2 2 non-
strictly determined game, the optimal mixed strategies for the players may be found
by employing the formulas contained in the following result, which we state without
proof.
526 9 MARKOV CHAINS AND THE THEORY OF GAMES
Optimal Strategies for Nonstrictly Determined Games
Let
be the payoff matrix for a nonstrictly determined game. Then, the optimal
mixed strategy for the row player is given by
P [ p
1
p
2
] (2a)
where
p
1
and p
2
1 p
1
and the optimal mixed strategy for the column player is given by
Q (2b)
where
q
1
and q
2
1 q
1
d b
a d b c
c
q
1
q
2
d
d c
a d b c
c
ab
cd
d
87533_09_ch9_p483-536 1/30/08 10:13 AM Page 526

The next example illustrates the use of these formulas in finding the optimal
mixed strategies and in finding the value of a 2 2 (nonstrictly determined) game.
APPLIED EXAMPLE 3
Coin-Matching Game (continued) Consider
the coin-matching game played by Richie and Chuck with the payoff
matrix
A
See Example 1.
a. Find the optimal mixed strategies for both Richie and Chuck.
b. Find the value of the game. Does it favor one player over the other?
Solution
a. The game under consideration has no saddle point and is accordingly non-
strictly determined. Using Formula (2a) with a 3, b 2, c 2, and
d 1, we find that
p
1
p
2
1 p
1
1
so Richie’s optimal mixed strategy is given by
P [p
1
p
2
]
Using (2b), we find that
q
1
q
2
1 q
1
1
giving Chuck’s optimal mixed strategy as
Q c
3
8
5
8
d
5
8
3
8
3
8
1 122
3 1 122 122
d b
a d b c
3
3
8
5
8
4
5
8
3
8
3
8
1 122
3 1 122 122
d c
a d b c
c
3 2
21
d
9.5 GAMES WITH MIXED STRATEGIES 527
Furthermore, the value of the game is given by the expected value of the game,
E PAQ, where P and Q are the optimal mixed strategies for the row and col-
umn players, respectively. Thus,
E PAQ
(2c)
ad bc
a d b c
87533_09_ch9_p483-536 1/30/08 10:13 AM Page 527

b. The value of the game may be found by computing the matrix product PAQ,
where P and Q are the vectors found in part (a). Equivalently, using (2c) we
find that
E
Since the value of the game is negative, we conclude that the coin-matching
game with the given payoff matrix favors Chuck (the column player) over
Richie. Over the long run, in repeated plays of the game, where each player
uses his optimal strategy, Chuck is expected to win
1
8
, or 12.5¢, on the average
per play.
APPLIED EXAMPLE 4
Investment Strategies As part of their invest-
ment strategy, the Carringtons have earmarked $40,000 for short-term
investments in the stock market and the money market. The performance of the
investments depends on the prime rate (that is, the interest rate that banks charge
their best customers). An increase in the prime rate generally favors their invest-
ment in the money market, whereas a decrease in the prime rate generally favors
their investment in the stock market. Suppose the following payoff matrix gives
the percentage increase or decrease in the value of each investment for each state
of the prime rate:
Prime rate Prime rate
up down
Money market investment
Stock market investment
a. Determine the optimal investment strategy for the Carringtons’ short-term
investment of $40,000.
b. What short-term profit can the Carringtons expect to make on their invest-
ments?
Solution
a. We treat the problem as a matrix game in which the Carringtons are the row
player. Letting p [ p
1
p
2
] denote their optimal strategy, we find that
p
1
[
a
15,
b
10,
c
5, and
d
25]
p
2
1 p
1
1
Thus, the Carringtons should put ($40,000), or approximately $34,300, into 1
6
7
2
1
7
6
7
30
35
6
7
d c
a d b c
25 152
15 25 10 152
c
15 10
525
d
1
8
13211 2 122122
3 1 122 122
ad bc
a d b c
528 9 MARKOV CHAINS AND THE THEORY OF GAMES
the money market and ($40,000), or approximately $5700, into the stock
market.
1
1
7
2
87533_09_ch9_p483-536 1/30/08 10:13 AM Page 528
b. The expected value of the game is given by
E
⬇ 12.14
Thus, the Carringtons can expect to make a short-term profit of 12.14% on
their total investment of $40,000—that is, a profit of (0.1214)(40,000), or
$4856.
425
35
1152125 2 1102152
15 25 10 152
ad bc
a d b c
9.5 GAMES WITH MIXED STRATEGIES 529
Explore & Discuss
A two-person, zero-sum game is defined by the payoff matrix
A
1. For what value(s) of x is the game strictly determined? For what value(s) of x is the
game not strictly determined?
2. What is the value of the game?
c
x 1 x
1 xx
d
9.5 Self-Check Exercises
9.5 Concept Questions
1. The payoff matrix for a game is given by
A
a. Find the expected payoff to the row player if the row
player R uses the maximin pure strategy and the column
player C uses the minimax pure strategy.
b. Find the expected payoff to the row player if R uses the
maximin strategy 40% of the time and chooses each of
the other two rows 30% of the time, while C uses the
minimax strategy 50% of the time and chooses each of
the other two columns 25% of the time.
c. Which pair of strategies favors the row player?
£
231
322
3 22
§
2. A farmer has allocated 2000 acres of her farm for planting
two crops. Crop A is more susceptible to frost than crop B.
If there is no frost in the growing season, then she can
expect to make $40/acre from crop A and $25/acre from
crop B. If there is mild frost, the expected profits are
$20/acre from crop A and $30/acre from crop B. How
many acres of each crop should the farmer cultivate in
order to maximize her profits? What profit could she
expect to make using this optimal strategy?
Solutions to Self-Check Exercises 9.5 can be found on
page 532.
1. What does the expected value of a game measure?
2. Suppose
c
ab
cd
d
is the payoff matrix for a nonstrictly determined game.
a. What is the optimal mixed strategy for the column
player?
b. What is the optimal mixed strategy for the row player?
c. What is the value of the game?
87533_09_ch9_p483-536 1/30/08 10:13 AM Page 529

530 9 MARKOV CHAINS AND THE THEORY OF GAMES
In Exercises 1–6, find the expected payoff E of each game
whose payoff matrix and strategies P and Q (for the row
and column players, respectively) are given.
1. , P , Q
2. , P [.8 .2], Q
3. , P , Q
4. , P , Q
5. , P [.2 .6 .2], Q
6. , P [.2 .3 .5], Q
7. The payoff matrix for a game is given by
Compute the expected payoffs of the game for the pairs of
strategies in parts (a–d). Which of these strategies is most
advantageous to R?
a. P [1 0], Q
b. P [0 1], Q
c. P , Q
d. P [.5 .5], Q
8. The payoff matrix for a game is
Compute the expected payoffs of the game for the pairs of
strategies in parts (a–d). Which of these strategies is most
advantageous to R?
a. P , Q £
1
3
1
3
1
3
§3
1
3
1
3
1
3
4
£
311
020
102
§
c
.8
.2
d
c
1
2
1
2
d3
1
2
1
2
4
c
1
0
d
c
1
0
d
c
1 2
23
d
£
.6
.2
.2
§£
1 42
211
2 20
§
£
.2
.6
.2
§£
202
1 13
214
§
c
1
3
2
3
d3
3
5
2
5
4c
12
31
d
c
3
4
1
4
d3
1
3
2
3
4c
43
21
d
c
.6
.4
dc
14
3 2
d
c
3
5
2
5
d3
1
2
1
2
4c
31
42
d
b. P , Q
c. P [.4 .3 .3], Q
d. P [.1 .5 .4], Q
9. The payoff matrix for a game is
a. Find the expected payoff to the row player if the row
player R uses the maximin pure strategy and the column
player C uses the minimax pure strategy.
b. Find the expected payoff to the row player if R uses the
maximin strategy 50% of the time and chooses each of
the other two rows 25% of the time, while C uses the
minimax strategy 60% of the time and chooses each of
the other columns 20% of the time.
c. Which of these pairs of strategies is most advantageous
to the row player?
10. The payoff matrix for a game is
a. Find the expected payoff to the row player if the row
player R uses the maximin pure strategy and the column
player C uses the minimax pure strategy.
b. Find the expected payoff to the row player if R uses the
maximin strategy 40% of the time and chooses each of
the other two rows 30% of the time, while C uses the
minimax strategy 50% of the time and chooses each of
the other columns 25% of the time.
c. Which of these pairs of strategies is most advantageous
to the row player?
In Exercises 11–16, find the optimal strategies, P and Q,
for the row and column players, respectively. Also com-
pute the expected payoff E of each matrix game and
determine which player it favors, if any, if the row and
column players use their optimal strategies.
11. 12. 13.
14. 15. 16. c
25
24
dc
2 6
8 4
dc
13
20
d
c
12
1 3
dc
25
3 6
dc
41
23
d
£
4 33
421
3 52
§
£
332
311
1 21
§
£
.3
.3
.4
§
£
.6
.2
.2
§
£
1
8
3
8
1
2
§3
1
4
1
2
1
4
4
9.5 Exercises
87533_09_ch9_p483-536 1/30/08 10:13 AM Page 530

17. Consider the coin-matching game played by Richie and
Chuck (see Examples 1 and 3) with the payoff matrix
A
a. Find the optimal strategies for Richie and Chuck.
b. Find the value of the game. Does it favor one player
over the other?
18. I
NVESTMENT
S
TRATEGIES
As part of their investment strat-
egy, the Carringtons have decided to put $100,000 into
stock market investments and also into purchasing pre-
cious metals. The performance of the investments depends
on the state of the economy in the next year. In an expand-
ing economy, it is expected that their stock market invest-
ment will outperform their investment in precious metals,
whereas an economic recession will have precisely the
opposite effect. Suppose the following payoff matrix gives
the expected percentage increase or decrease in the value
of each investment for each state of the economy:
Expanding Economic
economy recession
Stock market investment
Commodity investment
a. Determine the optimal investment strategy for the Car-
ringtons’ investment of $100,000.
b. What profit can the Carringtons expect to make on their
investments over the year if they use their optimal
investment strategy?
19. I
NVESTMENT
S
TRATEGIES
The Maxwells have decided to in-
vest $40,000 in the common stocks of two companies
listed on the New York Stock Exchange. One of the com-
panies derives its revenue mainly from its worldwide oper-
ation of a chain of hotels, whereas the other company is a
domestic major brewery. It is expected that if the economy
is in a state of growth, then the hotel stock should outper-
form the brewery stock; however, the brewery stock is
expected to hold its own better than the hotel stock in a
recessionary period. Suppose the following payoff matrix
gives the expected percentage increase or decrease in the
value of each investment for each state of the economy:
Expanding Economic
economy recession
Investment in hotel stock
Investment in brewery stock
a. Determine the optimal investment strategy for the
Maxwells’ investment of $40,000.
b. What profit can the Maxwells expect to make on their
investments if they use their optimal investment strategy?
20. C
AMPAIGN
S
TRATEGIES
Bella Robinson and Steve Carson are
running for a seat in the U.S. Senate. If both candidates cam-
paign only in the major cities of the state, then Robinson will
get 60% of the votes; if both candidates campaign only in the
rural areas, then Robinson will get 55% of the votes; if
Robinson campaigns exclusively in the city and Carson
c
25 5
10 15
d
c
20 5
10 15
d
c
4 2
21
d
campaigns exclusively in the rural areas, then Robinson will
get 40% of the votes; finally, if Robinson campaigns exclu-
sively in the rural areas and Carson campaigns exclusively
in the city, then Robinson will get 45% of the votes.
a. Construct the payoff matrix for the game and show that
it is not strictly determined.
b. Find the optimal strategy for both Robinson and Carson.
21. A
DVERTISEMENTS
Two dentists, Lydia Russell and Jerry
Carlton, are planning to establish practices in a newly
developed community. Both have allocated approximately
the same total budget for advertising in the local newspa-
per and for the distribution of fliers announcing their prac-
tices. Because of the location of their offices, Russell will
get 48% of the business if both dentists advertise only in
the local newspaper; if both dentists advertise through
fliers, then Russell will get 45% of the business; if Russell
advertises exclusively in the local newspaper and Carlton
advertises exclusively through fliers, then Russell will get
65% of the business. Finally, if Russell advertises through
fliers exclusively and Carlton advertises exclusively in the
local newspaper, then Russell will get 50% of the business.
a. Construct the payoff matrix for the game and show that
it is not strictly determined.
b. Find the optimal strategy for both Russell and Carlton.
22. Let
be the payoff matrix with a 2 2 matrix game. Assume
that either the row player uses the optimal mixed strategy
P [ p
1
p
2
], where
p
1
and p
2
1 p
1
or the column player uses the optimal mixed strategy
Q
where
q
1
and q
2
1 q
1
Show by direct computation that the expected value of the
game is given by E PAQ.
23. Let
be the payoff matrix associated with a nonstrictly deter-
mined 2 2 matrix game. Prove that the expected payoff
of the game is given by
E
Hint: Compute E PAQ, where P and Q are the optimal strate-
gies for the row and column players, respectively.
ad bc
a d b c
c
ab
cd
d
d b
a d b c
c
q
1
q
2
d
d c
a d b c
c
a
11
a
12
a
21
a
22
d
9.5 GAMES WITH MIXED STRATEGIES 531
87533_09_ch9_p483-536 1/30/08 10:13 AM Page 531
