Сучкова Л.И. Абстрактный и структурный синтез автоматов
Подождите немного. Документ загружается.

81
автомата. Переменные U
1
, U
2
, ... , U
h
используются в схеме
для обозначения сигналов, изменяющих состояние элементов
памяти, и называют функциями возбуждения. В качестве
элементов памяти на практике чаще всего используют эле-
ментарные автоматы, которые имеют только входные и вы-
ходные линии.
Каждое состояние абстрактного автомата a
i
кодируется
в структурных автоматах набором состояний элементов
па-
мяти ЭП
1
,…,ЭП
h
. Поскольку в качестве элементов памяти
используются обычные двоичные триггера, то каждое со-
стояние можно закодировать двоичным числом a
i
=Q
1
Q
2
….Q
h
.
Если все автоматы ЭП
1
...,ЭП
h
одинаковы, что в общем слу-
чае необязательно, то их число
R ≥ log
b
M
где M – число состояний синтезируемого автомата А, а b –
число состояний элементарного автомата памяти. Обычно
для элементарного автомата b=2, тогда R ≥ log
2
M.
В отличие от абстрактного автомата, имеющего один
входной и один выходной канал, структурный автомат имеет
L входных и N выходных каналов. Каждый входной и вы-
ходной сигналы абстрактного автомата могут быть закодиро-
ваны двоичным набором состояний входных и выходных ка-
налов структурного автомата. Число каналов L и N можно
определить по формулам
L
≥ ]log
2
m[;
N ≥
]log
2
k[,
где m и k – количество символов соответственно во
входном и выходном алфавитах абстрактного автомата.
Для того чтобы структурный автомат перешел из одного
состояния в другое, необходимо изменить состояние элемен-
тов памяти. Изменение же состояния элементов памяти про-
исходит под действием сигналов U
1
,…,U
h
, поступающих на
их входы. На вход комбинационной схемы, кроме
входного
сигнала, по цепи обратной связи поступают сигналы
Q
1
,…,Q
h
, называемые функцией обратной связи от памяти
82
автомата к комбинационной схеме.
Структурный синтез конечных автоматов заключается в
выборе типов элементарных автоматов, в составлении функ-
ций возбуждения каждого элементарного автомата и функ-
ций кодированных выходов автомата.
Рассмотрим примеры синтеза, которые позволяют
сформулировать общий алгоритм структурного синтеза ко-
нечных автоматов.
Выполним структурный синтез частичного автомата А,
заданного таблицами переходов и
выходов (рисунок 5.3).
a
1
a
2
a
3
a
4
z
1
a
1
/w
2
a
4
/w
1
a
4
/w
3
-/-
z
2
-/- a
3
/w
3
a
1
/w
1
-/-
z
3
a
2
/w
1
-/- a
2
/w
4
a
3
/w
2
Рисунок 5.3
Синтез будем выполнять в следующем порядке:
1. Выберем в качестве элемента памяти D-триггер.
2. Закодируем входные, выходные сигналы и внутрен-
ние состояния автомата. Количество входных абстрактных
сигналов = 3, следовательно количество входных структур-
ных сигналов L=]log
2
3[ = 2, т.е. х
1
, х
2
.
Количество выходных абстрактных сигналов G = 4, сле-
довательно количество выходных структурных сигналов N
=]log
2
G[ = ]log
2
4[ = 2, т.е. у
1
, у
2
. Количество внутренних со-
стояний абстрактного автомата M = 4, следовательно коли-
чество двоичных элементов памяти (триггеров) R = ] log
2
M [
= ]log
2
4[ = 2.
83
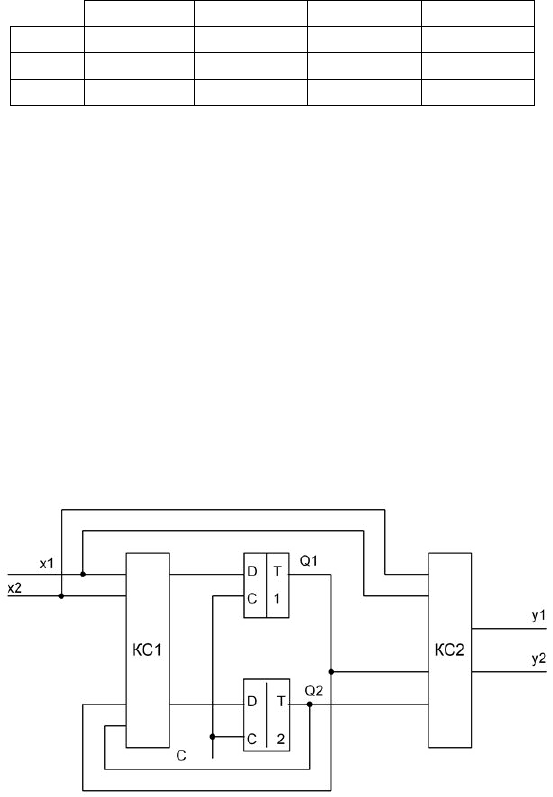
Структура автомата с учетом того, что исходный авто-
мат является автоматом Мили, в качестве элементов памяти
используется D-триггер, может быть представлена в виде
(рисунок 5.4):
Рисунок 5.4 - Структура синтезируемого автомата
Кодирование входных, выходных сигналов и внутрен-
них состояний представлено в таблицах:
Кодирование, в общем случае, осуществляется произ-
вольно
. Поэтому, например, каждому из сигналов z
i
можно
поставить в соответствие любую двухразрядную комбина-
цию х
1
, х
2
. Необходимо только, чтобы разные выходные сиг-
налы z
i
кодировались разными комбинациями х
1
, х
2
.. Анало-
гично для w
i
и a
i
.
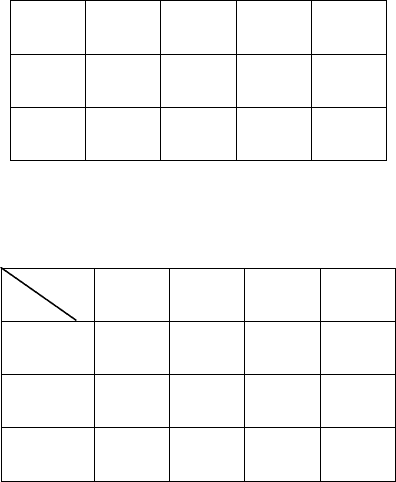
3. Получим кодированные таблицы переходов и выхо-
дов структурного автомата. Для этого в таблицах переходов
и выходов исходного абстрактного автомата вместо z
i
, w
i
, a
i
cтавим соответствующие коды. Получим таблицы:
a
1
a
2
a
3
a
4
Q
1
Q
2
x
1
x
2
00 01 11 10
x
1
x
2
z
1
0 0
z
2
0 1
z
3
1 1
y
1
y
2
w
1
0 0
w
2
0 1
w
3
1 1
w
4
1 0
Q
1
Q
2
a
1
0 0
a
2
0 1
a
3
1 1
a
4
1 0
84
00 00 10 10 -
01 - 11 00 -
11 01 - 01 11
Кодированная таблица переходов
a
1
a
2
a
3
a
4
Q
1
Q
2
x
1
x
2
00 01 11 10
00 01 00 11 -
01 - 11 00 -
11 00 - 10 01
Кодированная таблица выходов.
В кодированной таблице переходов заданы функции:
Q
1
t+1
=ψ
1
(x
1
, x
2
, Q
t
1
, Q
t
2
),
Q
2
t+1
=ψ
2
(x
1,
x
2,
Q
1
t+1
, Q
2
t+1
).
В кодированной таблице выходов заданы функции:
y
1
=
φ
1
(x
1,
x
2
, Q
1
t
, Q
2
t
), y
2
=
φ
2
(x
1
, x
2
, Q
1
t
, Q
2
t
).
4. При каноническом методе надо получить функции
y
1
=
φ
1
(x
1
, x
2
, Q
1
, Q
2
),
y
2
=
φ
2
(x
1
, x
2
, Q
1
, Q
2
),
D
1
= f
1
(x
1
, x
2
, Q
1
, Q
2
),
D
2
= f
2
(x
1
, x
2
, Q
1
, Q
2
),
где D
1
и D
2
- функции возбуждения элементов памяти,
а затем построить комбинационные схемы, реализующие

85
данную систему булевых функций.
Функции у
1
и у
2
могут быть непосредственно получены
из таблицы выходов, например, в виде (смотрим по всем 1 в
таблице выходов соответственно для первого и второго зна-
чений из пары в клетке таблицы):
y
1
= x
1
x
2
Q
1
Q
2
+ x
1
x
2
Q
1
Q
2
+ x
1
x
2
Q
1
Q
2
y
2
= x
1
x
2
Q
1
Q
2
+ x
1
x
2
Q
1
Q
2
+ x
1
x
2
Q
1
Q
2
+ x
1
x
2
Q
1
Q
2
Однако выражения для у
1
и у
2
можно существенно упро-
стить в результате минимизации, например, с помощью карт
Карно.
Рассмотрим построение и использование карт Карно для
минимизации функций. Двухмерные таблицы для переклю-
чательных функций, которые называют диаграммами Вейча
или картами Карно, обычно строят, записывая значения ар-
гументов в строках и столбцах таблицы таким образом, что-
бы наборы
аргументов, отличающиеся значением только од-
ной переменной, располагались симметрично относительно
какой-либо оси симметрии. Для построения диаграмм, обла-
дающих свойством симметрии, значения переменных запи-
сывают в строках и столбцах таблицы в порядке, соответст-
вующем зеркальному коду (цикличному коду, коду Грея).
Такой код строится согласно следующим правилам:
1. Коды единичной длины
(n=1) являются зеркальными.
2. Если построен код длины (n-1), то нужно построить
новую ось симметрии и отобразить зеркально коды длины (n-
1) относительно этой оси, а затем приписать слева всем ко-
дам, расположенным выше оси, цифру 0, а кодам, располо-
женным, ниже оси, цифру 1. В результате получаем зеркаль-
ные коды длины n. Процесс построения зеркальных кодов
для n = 1,2,3 показан ниже:

86
Рассмотрим визуальный метод минимизации булевых
функций с помощью карт Карно, который является одним из
наиболее удобных методов при небольшом числе перемен-
ных (до 6). Данный метод был разработан в 1953 г. амери-
канским ученым Морисом Карно.
Карта Карно является координатным способом пред-
ставления булевых функций. При этом способе задания таб-
лица
истинности функции представляется в виде координат-
ной карты состояний, которая содержит 2
n
клеток (по числу
входных наборов булевой функции n переменных). Перемен-
ные функции разбиваются на две группы так, что одна груп-
па определяет координаты столбца карты, а другая - коорди-
наты строки. При таком способе построения каждая клетка
определяется значениями переменных, соответствующих оп-
ределенному двоичному набору. Внутри каждой клетки кар-
ты Карно ставится
значение функции на данном наборе. Пе-
ременные в строках и столбцах располагаются так, чтобы
соседние клетки карты Карно различались только в одном
разряде переменных, т.е. были соседними. Поэтому значения
переменных в столбцах и в строках карты образуют соседний
код Грея.
Правила минимизации с использованием карт Кар-
но:
1. В карте
Карно группы единиц (для получения дизъ-
n=1 n=2 n=3
0
1
Ось
симметрии
00
01
11
10
Ось
симметрии
000
001
011
010
110
111
101
100
Ось
симметрии
87
юнктивной нормальной формы (ДНФ)) и группы нулей (для
получения конъюнктивной нормальной формы (КНФ)) необ-
ходимо обвести четырехугольными контурами. Внутри кон-
тура должны находится только одинаковые значения функ-
ции. Этот процесс соответствует операции склеивания или
нахождения импликант данной функции. Импликанта – эле-
ментарное произведение, равное 1 на наборах, где функция
равна 1, и 0 на наборах
, где функция равна 0.
2. Количество клеток внутри контура должно быть це-
лой степенью двойки (1, 2, 4, 8, 16...).
3. При проведении контуров крайние строки карты
(верхние и нижние, левые и правые), а также угловые клетки,
считаются соседними (для карт до 4-х переменных).
4. Каждый контур должен включать максимально воз-
можное количество клеток. В этом случае
он будет соответ-
ствовать простой импликанте, к которой нельзя применить
операцию склеивания.
5. Все единицы (нули) в карте (даже одиночные) долж-
ны быть охвачены контурами. Любая единица (нуль) может
входить в контуры произвольное количество раз.
6. Множество контуров, покрывающих все 1 (0) функ-
ции образуют тупиковую ДНФ (КНФ). Целью минимизации
является нахождение минимальной из
множества тупиковых
форм. Форма называется тупиковой, если представляет собой
дизъюнкцию простых импликант, из которых ни одна не яв-
ляется лишней.
7. В элементарной конъюнкции (дизъюнкции), которая
соответствует одному контуру, остаются только те перемен-
ные, значение которых не изменяется внутри обведенного
контура. Переменные булевой функции входят в элементар-
ную конъюнкцию (для значений
функции 1) без инверсии,
если их значение на соответствующих координатах равно 1 и
с инверсией - если 0. Для значений булевой функции, равных
0, записываются элементарные дизъюнкции, куда перемен-
ные входят без инверсии, если их значение на соответствую-
щих координатах равно 0 и с

88
инверсией - если 1.
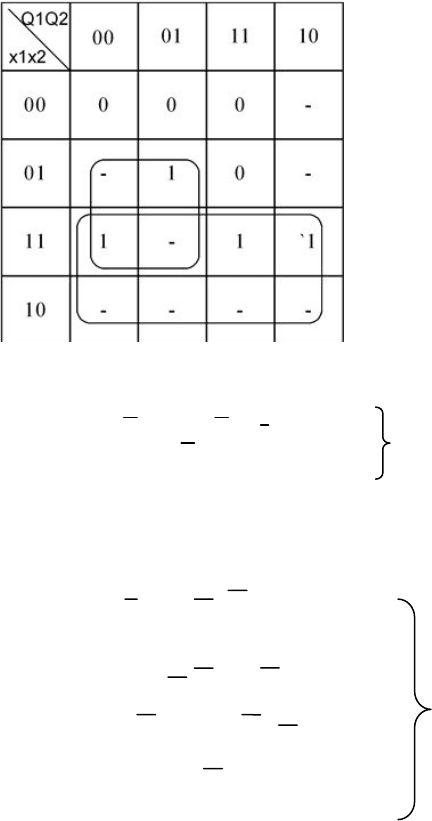
Для нашего примера карты Карно для y
1
и y
2
приведе-
ны на рисунках 5.5 и 5.6.
Рисунок 5.5 - Карта Карно для y
1
Рисунок 5.6 - Карта Карно для y
2
В результате минимизации имеем:
y
1
= x
2
Q
1
+ x
1
Q
2
+ x
1
x
2
Q
1
(*)

89
y
2
= x
2
Q
1
+ Q
1
Q
2
+ x
2
Q
2
+ x
1
x
2
Q
1
Для получения выражений для D
1
и D
2
необходимо
получить таблицы функций возбуждения. Для этого необхо-
димо воспользоваться кодированной таблицей переходов и
функциями входов элементов памяти. Зная код исходного
состояния автомата (код Q
t
– из какого состояния переход) и
код состояния перехода (Q
t+1
– в какое состояние перехо-
дим) на основании таблицы
функции входов триггера полу-
чаем требуемое значение функции возбуждения D
t
, пода-
ваемое на вход триггера и обеспечивающее заданный пере-
ход. Для D-триггеров таблица переходов совпадает с табли-
цей функции возбуждения. Тогда либо непосредственно из
этой таблицы, либо в результате минимизации получаем
требуемые значения D
i
. Обычно используется минимизация
с помощью
карт Карно. Для нашего примера карты Карно
для y
1
и y
2
приведены на рисунках 5.7 и 5.8.
Рисунок 5.7 - Карта Карно для D
1
90
Рисунок 5.8 - Карта Карно для D
2
В результате минимизации получаем:
D
1
= Q
1
Q
2
+ Q
1
Q
2
+ x
2
Q
2
D
2
= x
1
+ x
2
Q
1
5. На основании полученных в результате синтеза буле-
вых выражений ((*), (**)) ,строим функциональную схему
автомата. Для этого уравнения ((*), (**)) представим в виде:
P = x
2
Q
1
+ x
1
x
2
Q
y
1
= P + x
1
Q
2
y
2
= P + x
2
Q
2
+ Q
1
Q
2
D
1
= Q
1
Q
2
+ Q
1
Q
2
+ x
2
Q
2
D
2
= x
1
+ x
2
Q
1
Функциональная схема автомата представлена на рисун-
ке 5.9.
Дополнительно на функциональной схеме показан
(**)
