Строев, О.Я. Надежность информационных систем
Подождите немного. Документ загружается.

Министерство транспорта Российской Федерации
Федеральное агентство железнодорожного транспорта
ГОУ ВПО «Дальневосточный государственный
университет путей сообщения»
Кафедра «Телекоммуникаций»
О.Я. Строев
НАДЕЖНОСТЬ
ИНФОРМАЦИОННЫХ СИСТЕМ
Методические указания
к курсовому проектированию
Хабаровск
Издательство ДВГУПС
2008

2
УДК 621.391:004(075.8)
ББК З 88-01 я 73
С 862
Рецензент:
Доктор технических наук,
заведующий кафедрой «Автоматика и телемеханика»
Дальневосточного государственного университета путей сообщения,
профессор А.И. Годяев
С 862
Строев, О.Я.
Надежность информационных систем : метод. указания к курсо-
вому проектированию / О.Я. Строев. – Хабаровск : Изд-во ДВГУПС,
2008. – 28 с. : ил.
Методические указания соответствуют ГОС ВПО направления подго-
товки дипломированных специалистов 190400 «Системы обеспечения
движения поездов» специальности 190402 «Автоматика, телемеханика и
связь на железнодорожном транспорте».
Включают информацию по расчету основных параметров и харак-
теристик надежности сложных систем с произвольной конфигурацией
структуры.
Методические указания предназначены для студентов 4-го курса всех
форм обучения, изучающих дисциплину «Основы теории надежности».
Отпечатано методом прямого репродуцирования
УДК 621.391(075.8)
ББК З 88-01 я 73
© ГОУ ВПО «Дальневосточный государственный
университет путей сообщения» (ДВГУПС), 2008
3
ВВЕДЕНИЕ
С появлением сложных электронных систем, проблеме надежности
стали уделять большое внимание. Надежность – свойство прибора, обу-
словленное, главным образом, его безотказностью в течение определен-
ного времени. Количественно надежность определяется вероятностными
характеристиками и параметрами.
Отказ – полная или частичная утрата работоспособности прибора. Раз-
личают несколько типов отказов:
– полный отказ, при котором использование прибора по назначению
невозможно. Полные отказы обычно наступают внезапно в результате
значительного скачкообразного изменения одного или нескольких основ-
ных параметров, например, пробоя перехода в транзисторе, выхода из
строя микросхемы и т.д.
– постепенный (частичный) отказ, возникающий в результате постепен-
ного изменения одного или нескольких основных параметров. Поскольку
величина ухода параметра прибора, вызывающего отказ аппаратуры, за-
висит от схемы устройства, где на отклонившийся от нормы параметр на-
ложены меньшие ограничения.
Что же может быть причиной отказа? Перечислим некоторые из них:
ошибка проектировщика, ошибка сборки, скрытые дефекты элементов, не-
благоприятные сочетания отклонений питающих напряжений, статическое
электричество и ряд других.
Отметим, что для поддержания надежности на должном уровне осуще-
ствляется: заменой, восстановлением.

4
МЕТОДЫ РАСЧЕТА НАДЕЖНОСТИ
Один из основных критериев надежности – вероятность безотказной
работы p(t) прибора – определяется вероятностью того, что в пределах
заданной продолжительности работы t отказ не возникнет. Эксперимен-
тально вероятность безотказной работы можно оценить как:
N
n
)t(p = , (1)
где N – число испытываемых приборов; n – число годных приборов к мо-
менту времени t.
Вероятность отказа до момента времени t – q(t) есть противоположное
событие, следовательно,
)
(
)
(
1
t
p
t
q
−
=
. (2)
Вероятность q(t) представляет собой интегральный закон распределе-
ния моментов отказов.
Функция плотности вероятностей моментов отказов ω
0
(t) по определе-
нию есть производная интегрального закона, следовательно,
)t(p)t('q)t( '
0
−
=
=
ω
. (3)
Интенсивность отказов λ(t) – условная плотность вероятности отказа в
момент времени t при условии, что элемент до этого момента работал
безотказно, определяется выражением:
)t(p
)t('p
)t(p
)t(
)t( −=
ω
=λ
0
. (4)
Используя оценку (1) и определение (4), дадим оценку интенсивности
отказов:
dt
dn
nNndt
Ndn
)t(p
)t('p 1
−=
⋅
⋅
−=−=λ , (5)
т.е. интенсивность отказов равна относительному числу приборов, отка-
завших в единицу времени.
Связь между интенсивностью отказов и вероятностью безотказной ра-
боты, а также вероятностью появления отказа выражается так:
t
e)t(P
λ−
= , (6)
t
e)t(Q
λ−
−=1 , (7)
Выбор математической модели отказов опирается на опыт эксплуата-
ции, согласно которому в работе большинства электронных приборов
имеются три периода:
5
– приработка, когда преобладают начальные отказы, вызванные скры-
тыми дефектами; их интенсивность монотонно уменьшается;
– нормальная эксплуатация, когда интенсивность отказов остается
практически постоянной или медленно уменьшается;
– износ (старение), когда начинают сказываться постепенные отказы.
Универсальным методом расчета надежности любой системы со слож-
ной логической структурой является метод полной группы событий. Всего
существует 2
n
состояний, которые образуют полную группу событий пред-
ставленных таблицей. В столбце R
i
указаны вероятности событий A
i
,
при-
чем сумма этих вероятностей равна 1. В результате появления события A
i
система может оказаться работоспособной в момент t (S = 1) или нерабо-
тоспособной (S = 0).
Таким образом, надежность сложной системы есть функция алгебры
логики от надежности ее элементов. Вероятность безотказной работы сис-
темы будет равна сумме вероятностей тех событий A
i
, для которых S = 1:
)t(R)t(Р
i
∑
=
1
. (8)
Рассмотрим один из примеров расчета структурной и алгоритмической
надежности.
ЗАДАНИЕ 1
Нормально функционирующее изделие всегда может быть представ-
лено, как некоторая структура, целесообразно составленная из ряда взаи-
мосвязанных элементов. Логические, структурные схемы расчета надеж-
ности необязательно совпадают
со структурной схемой самого из-
делия. Для расчета надежности
необходимо знать интенсивности
отказа или безотказной работы
элементов, и время работы.
Интенсивности безотказной ра-
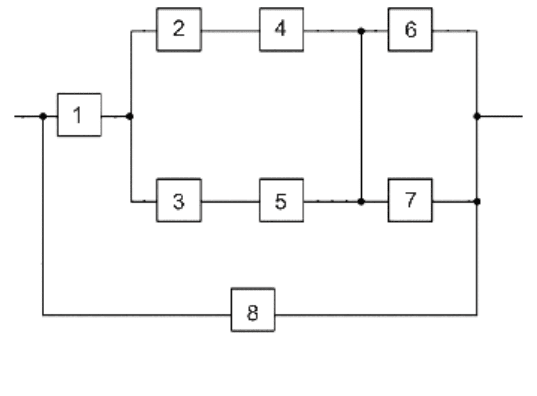
боты элементов (рис. 1):
5
1
10392
−
⋅=λ . ;
5
2
10514
−
⋅=λ . ;
5
3
10436
−
⋅=λ . ;
5
4
10338
−
⋅=λ . ;
5
5
104310
−
⋅=λ . ;
5
6
105312
−
⋅=λ . ;
5
7
102315
−
⋅=λ . .
Время работы: t = 1000 часов.
Необходимо:
– сформулировать условия безотказной работы при одинаковом t;
– рассчитать общую надежность изделия;
Рис. 1. Структурная схема изделия
6
– определить среднее время наработки до первого отказа;
– определить среднее время наработки на отказ;
– определить интенсивность отказа каждого элемента;
– построить графики функций надежности и ненадежности.
Перед расчетом сформулируем условие безотказной работы: устройст-
во безотказно работает, если в безотказном состоянии будет находиться
элемент 1 и 2, и 4, или 3 и 5, и 6 или 7, или хотя бы элемент 8.
Так как в нашем изделии элементы имеют последовательно-парал-
лельные соединения, то можно применить метод преобразования струк-
турной схемы (метод сверки), объединяя элементы в более крупные блоки
и применяя формулы расчета для элементарных схем надежности.
Для последовательного соединения:
2112
ppP
=
.
Для параллельного соединения:
21212112
111 pppp)p)(p(P
−
+
=
−
−
−
=
.
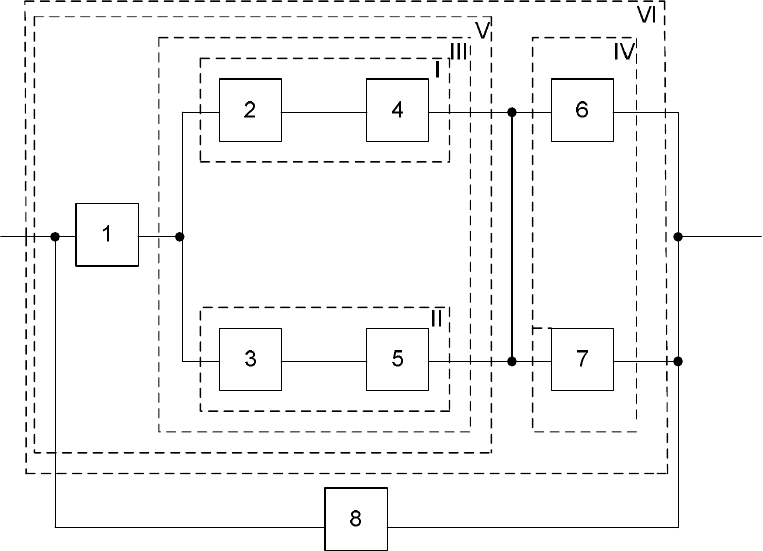
Произведем декомпозицию структурной схемы, для чего разобьем ее
на последовательные и параллельные соединения элементов (рис. 2).
Рис. 2. Структурная схема изделия после декомпозиции
Далее необходимо рассчитать вероятность безотказной работы каждо-
го отдельного элемента по формуле:
t-
eP(t)
λ
=
.

7
Таким образом, имеем:
100010392
1
5
(1000)
⋅⋅−
−
=
.
eP = 0.976 , аналогично вычисляем надежности ос-
тальных элементов, в результате чего получаем:
=
(1000)
2
P 0,956;
=
(1000)
3
P 0,938;
=
(1000)
4
P 0,92;
=
(1000)
5
P 0,9;
=
(1000)
6
P 0,882;
=
(1000)
7
P 0,859.
Рассчитаем надежности структурных блоков, представленных на схе-
ме. Параллельное соединение равнозначно функции дизъюнкции, а по-
следовательное – конъюнкции.
8795209209560(1000)(1000)(1000)
42I
...PPP
=
⋅
=
⋅
=
;
84420909380(1000)(1000)(1000)
53
...PPP
II
=
⋅
=
⋅
=
;
981230(1000)(1000)(1000)(1000)(1000) .PPPPP
IIIIIIIII
=
⋅
−
+
=
;
98340(1000)(1000)(1000)(1000)(1000)
7676
.PPPPP
IV
=
⋅
−
+
=
;
9576809812309760(1000)(1000)(1000) ...PPP
IIIIV
=
⋅
=
⋅
=
;
9417095768098340(1000)(1000)(1000) ...PPP
VIVVI
=
⋅
=
⋅
=
;
94170(1000)
8
.P
=
;
99660(1000)(1000)(1000)(1000)(1000)
88VI
.PPPPP
VIобщ
=
⋅
−
+
=
.
Исходя из полученной вероятности всего изделия, получим его интен-
сивность:
6
103.41
1000)(
1
−
⋅=
−
⋅=λ
общ
Pln
.
Среднее время наработки на отказ:
13293255
6
10
41
3
1
1
.
.
T
ср
=
−
⋅
=
λ
= часов.
Функции надежности и ненадежности выглядят следующим образом:
t.
e)t(P
⋅⋅−
−
=
6
10413
,
t.
e)t(Q
⋅⋅−
−
−=
6
10413
1 .

8
Таблица 1
Расчет функции надежности для различных значений t
t, ч P(t)
1 0,999996
10 0,9999659
50 0,9998
100 0,99966
1000 0,996596
10000 0,966475
100000 0,7110589
150000 0,599596
200000 0,5056
250000 0,42635
300000 0,3595
350000 0,3032
400000 0,25564
Таблица 2
Расчет функции ненадежности для различных значений t
t, ч P(t)
10000 0.0335
100000 0.2889
150000 0.4
200000 0.49
250000 0.5737
300000 0.64
350000 0.6968
400000 0.744
1000000 0.96696
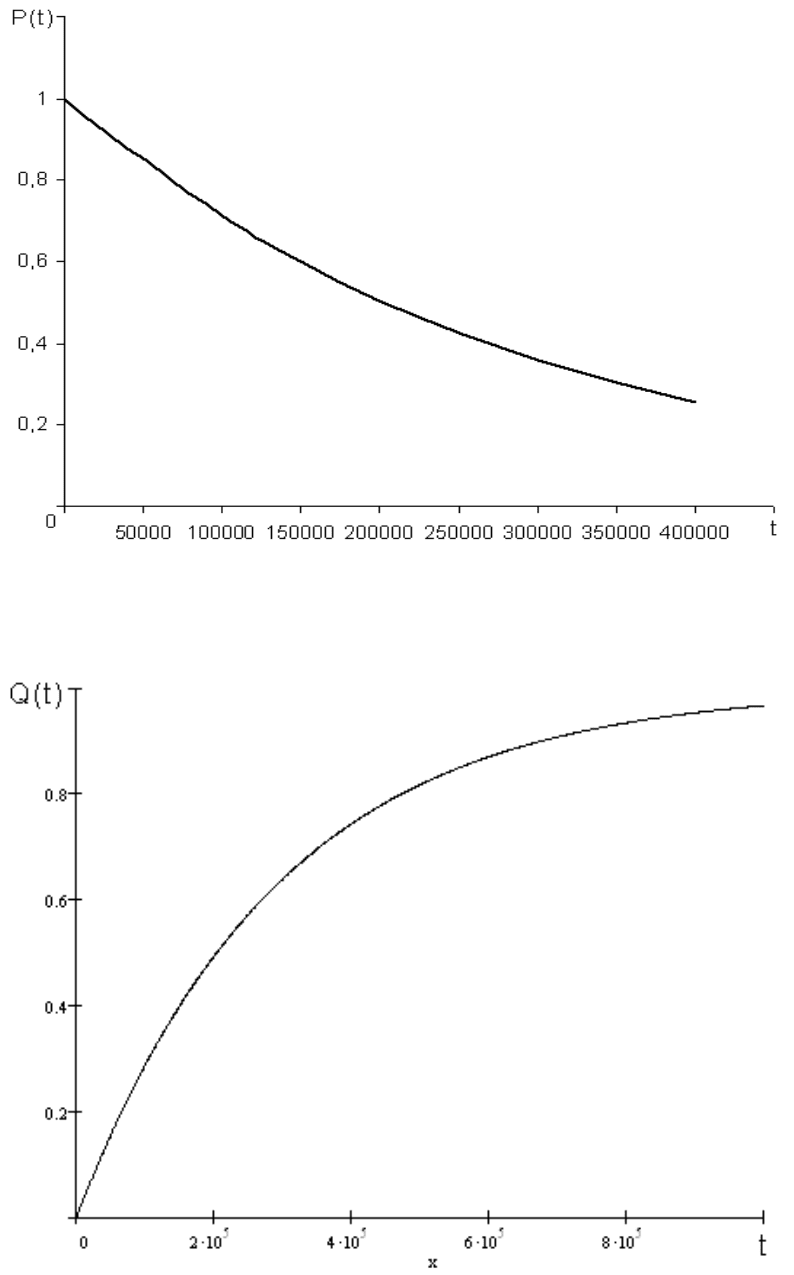
По полученным таблицам построим функции надежности и ненадежно-
сти (рис. 3 и 4).
Из вышеприведенных расчетов и построенных графиков, очевидно,
что выполняется одно из основных положений теории надежности: при
параллельном соединении элементов общая надежность всегда выше
надежности самого надежного элемента, а при последовательном соеди-
нении общая надежность всегда меньше надежности самого ненадежного
элемента.
9
Рис. 3. Функция надежности
Рис. 4. Функция ненадежности
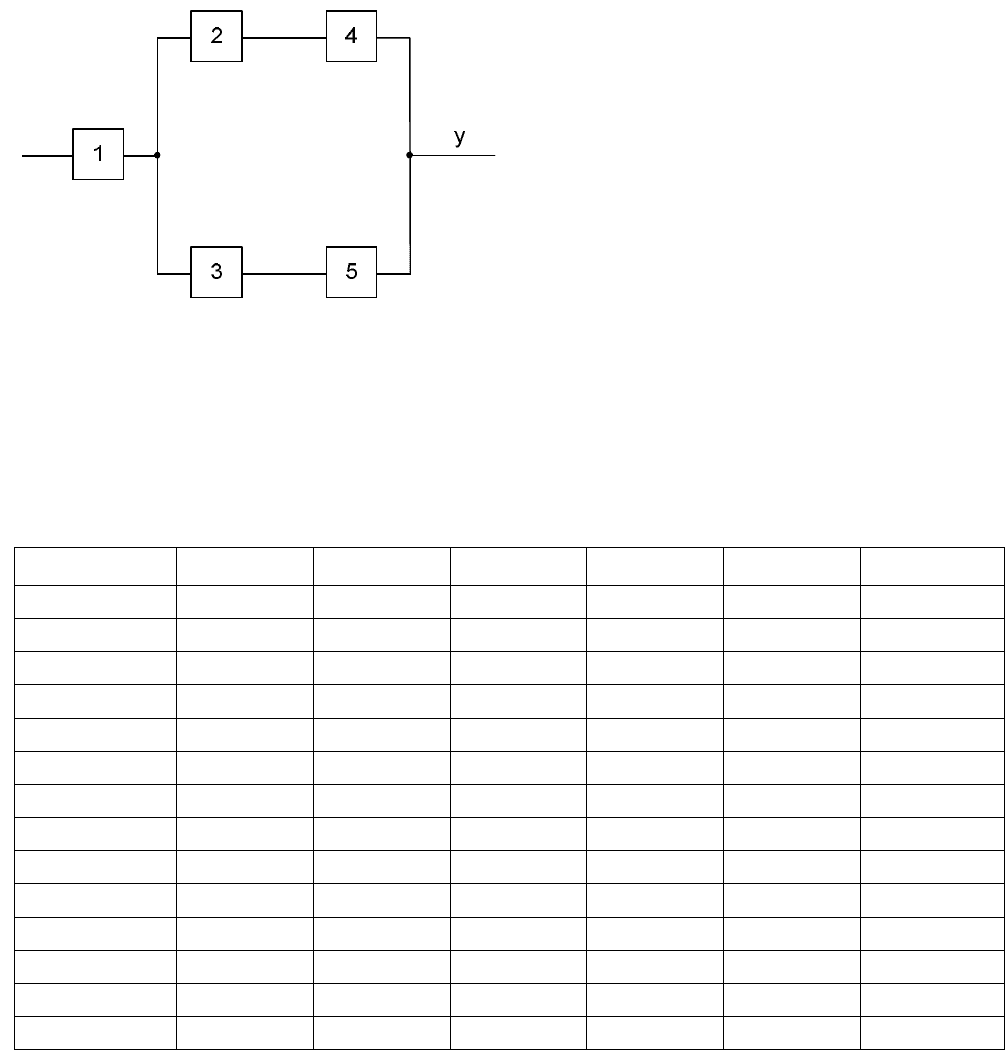
10
ЗАДАНИЕ 2
Необходимо:
– Выбрать в структурной схеме (первое задание) расчёта участок из
пяти элементов.
– Произвести расчёт функции надёжности и ненадёжности (построить
графики) изделия, интенсивность отказа изделия, среднее время наработ-
ки на отказ табличным методом для выбранного участка.
– Сравнить результаты, полученные в первом и втором заданиях.
И теоретически, и практически
табличный метод вычисления
структурной надежности является
универсальным, то есть он приго-
ден для расчета системы любой
сложности и конфигурации.
Выбираем участок структурной
схемы изделия из первого задания
(рис. 5).
В любой строке обозначается
один из 2
n
состояний, где n – число
элементов. Множество 2
n
состоя-
ний представляет собой полную группу несовместных сложных событий.
Выход у характеризует состояние схемы: на выходе у будет 1, если в
безотказном состоянии находятся элементы 1 и 2, и 4, или 3 и 5.
Таблица 3
Состояние системы
№ такта 1 2 3 4 5
Выход у
0 0 0 0 0 0 0
1 0 0 0 0 1 0
2 0 0 0 1 0 0
3 0 0 0 1 1 0
4 0 0 1 0 0 0
5 0 0 1 0 1 0
6 0 0 1 1 0 0
7 0 0 1 1 1 0
8 0 1 0 0 0 0
9 0 1 0 0 1 0
10 0 1 0 1 0 0
11 0 1 0 1 1 0
12 0 1 1 0 0 0
13 0 1 1 0 1 0
Окончание табл. 3
Рис. 5. Участок структурной схемы изделия
