Строев, О.Я. Надежность информационных систем
Подождите немного. Документ загружается.

11
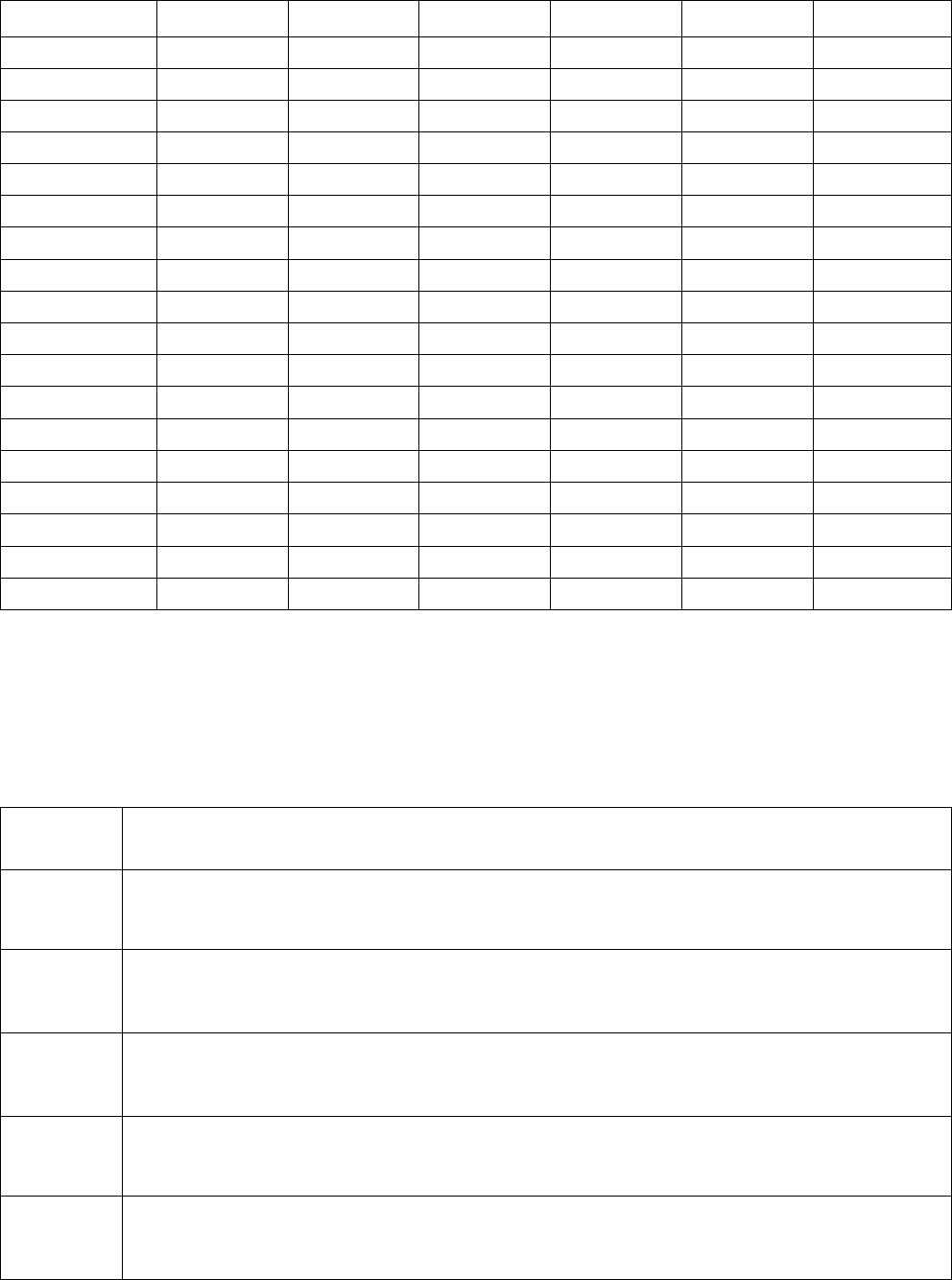
№ такта 1 2 3 4 5
Выход у
14 0 1 1 1 0 0
15 0 1 1 1 1 0
16 1 0 0 0 0 0
17 1 0 0 0 1 0
18 1 0 0 1 0 0
19 1 0 0 1 1 0
20 1 0 1 0 0 0
21 1 0 1 0 1 1
22 1 0 1 1 0 0
23 1 0 1 1 1 1
24 1 1 0 0 0 0
25 1 1 0 0 1 0
26 1 1 0 1 0 1
27 1 1 0 1 1 1
28 1 1 1 0 0 0
29 1 1 1 0 1 1
30 1 1 1 1 0 1
31 1 1 1 1 1 1
Вероятность безотказной работы определяется как сумма вероятно-
стей безотказных несовместных случайных событий, расчет которых пред-
ставлен в табл. 4.
Таблица 4
Расчет вероятности безотказной работы
№
такта
Вероятности безотказной работы
21
0029
0
9
0
08
0
938
0
044
0
976
0
)()()()()()(
5432121
.
.
.
.
.
.
tPtQtPtQtPtP
=
⋅
⋅
⋅
⋅
=
=
⋅
⋅
⋅
⋅
=
23
0334090920938004409760
)()()()()()(
5432123
......
tPtPtPtQtPtP
=⋅⋅⋅⋅=
=
⋅
⋅
⋅
⋅
=
26
00532010920062095609760
)()()()()()(
5432126
......
tQtPtQtPtPtP
=⋅⋅⋅⋅=
=
⋅
⋅
⋅
⋅
=
27
0479
0
9
0
92
0
062
0
956
0
976
0
)()()()()()(
5432127
.
.
.
.
.
.
tPtPtQtPtPtP
=
⋅
⋅
⋅
⋅
=
=
⋅
⋅
⋅
⋅
=
29
063090080938095609760
)()()()()()(
5432129
......
tPtQtPtPtPtP
=⋅⋅⋅⋅=
=
⋅
⋅
⋅
⋅
=
Окончание табл. 4

12
№
такта
Вероятности безотказной работы
30
08052010920938095609760
)()()()()()(
5432130
......
tQtPtPtPtPtP
=⋅⋅⋅⋅=
=
⋅
⋅
⋅
⋅
=
31
725
0
9
0
92
0
938
0
956
0
976
0
5432131
.
.
.
.
.
.
tPtPtPtPtPtP
=
⋅
⋅
⋅
⋅
=
=
⋅
⋅
⋅
⋅
=
)()()()()()(
Таким образом, вероятности безотказной работы и отказа всего изделия:
)()()()()()()()( tPtPtPtPtPtPtPtP
общ 31302927262321
+
+
+
+
+
+
=
.
За время T = 1000 часов
;957707250080520063004790
005300334000290(1000)(1000)(1000)
(1000)(1000)(1000)(1000)(1000)
313029
27262321
.....
...PPP
PPPPP
общ
=++++
+++=+++
+
+
+
+
=
...PQ
общобщ
04230957701)1000(1)1000(
=
−
=
−
=
Интенсивность отказа изделия находится как:
5
10324
1000
(0.9577)
1000
(1000))(
−
⋅=
−
=
−
=λ .
ln
Pln
общ
1/ч.
Среднее время наработки на отказ:
1523148
10324
11
5
.
.
T
ср
=
⋅
=
λ
=
−
часов.
Очевидным является то, что вероятность безотказной работы изделия,
рассчитанного во втором задании, равна вероятности безотказной работы
блока V изделия, рассматриваемого в первом задании. При этом видно,
что расчет табличным методом значительно проще, чем классический ме-
тод расчета.
При сравнении полученных результатов видно, что надежность данного
изделия меньше, чем изделия, рассчитанного в первом задании, так как у не-
го отсутствует дублирующий элемент. Также у данного изделия на порядок
меньше среднее время наработки на отказ и больше интенсивность отказов.
ЗАДАНИЕ 3
Для мостовой схемы необходимо:
– рассчитать общую надежность изделия;
– определить среднее время наработки до первого отказа;
– определить среднее время наработки на отказ каждого элемента;
– определить интенсивность отказа каждого элемента;
– построить графики функций надежности и ненадежности;
13
– полученные результаты сравнить с характеристиками пятью после-
довательно соединённых элементов (с теми же интенсивностями отказа).
Интенсивность отказа элементов берем из первого задания и время
работы 1000 часов.
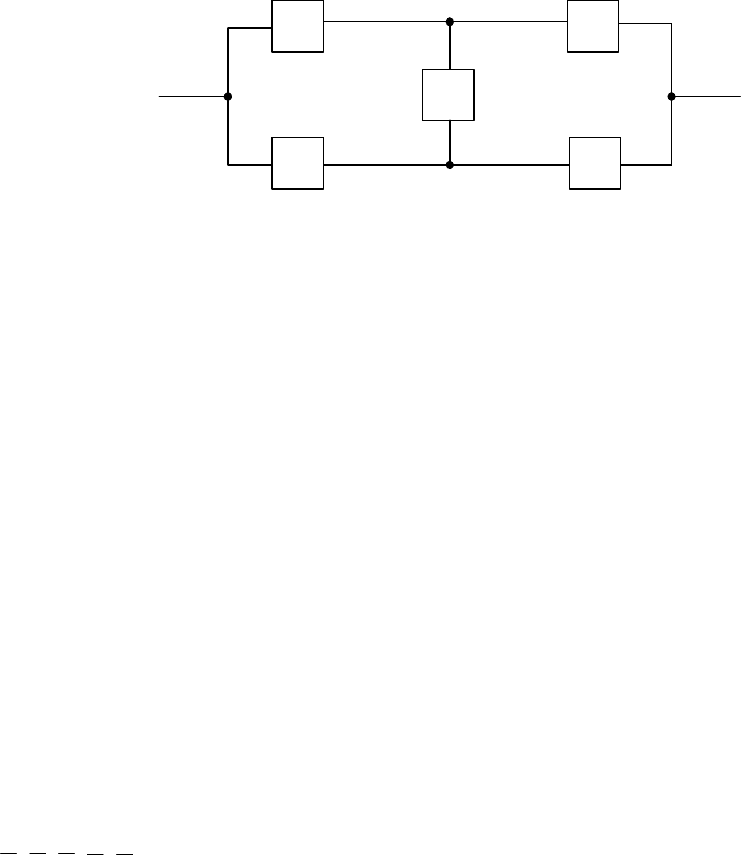
1 2
3 4
5
Рис. 6. Мостовая схема
Приведем вероятности безотказной работы и отказа каждого элемента:
9760)1000(
1
.P
=
; 0240)1000(
1
.q
=
;
9560)1000(
2
.P
=
; 0440)1000(
2
.q
=
;
9380)1000(
3
.P
=
; 0620)1000(
3
.q
=
;
920)1000(
4
.P
=
; 080)1000(
4
.q
=
;
90)1000(
5
.P
=
; 10)1000(
5
.q
=
.
Известно, что для информационных и глобальных систем характерны
мостовые структуры.
Наиболее удобным для расчета структурной надежности мостовых
схем, является метод с использованием таблиц состояний системы.
Воспользуемся понятиями теории конечных автоматов. Составим таб-
лицу состояний элементов и состояния изделия в целом. Все наборы про-
нумеруем и упорядочим.
Примем:
1,2,3,4,5 – безотказное состояние элементов (то есть = 1);
54321 ,,,, – отказ этих элементов (то есть = 0);
Y = 1 – изделие, в котором нет отказа элементов;
Y = 0 – отказ элементов.
Также следует указать, что число состояний m = 2, количество элемен-
тов n = 5, отсюда следует: k =
32
2
5
=
=
n
m
.
При этом, для удобства, можно в конце подсчитать только безотказную
работу P(Y) или отказ Q(Y), чтобы сократить объем вычислений (в нашем
случае рассчитаем P(Y)).
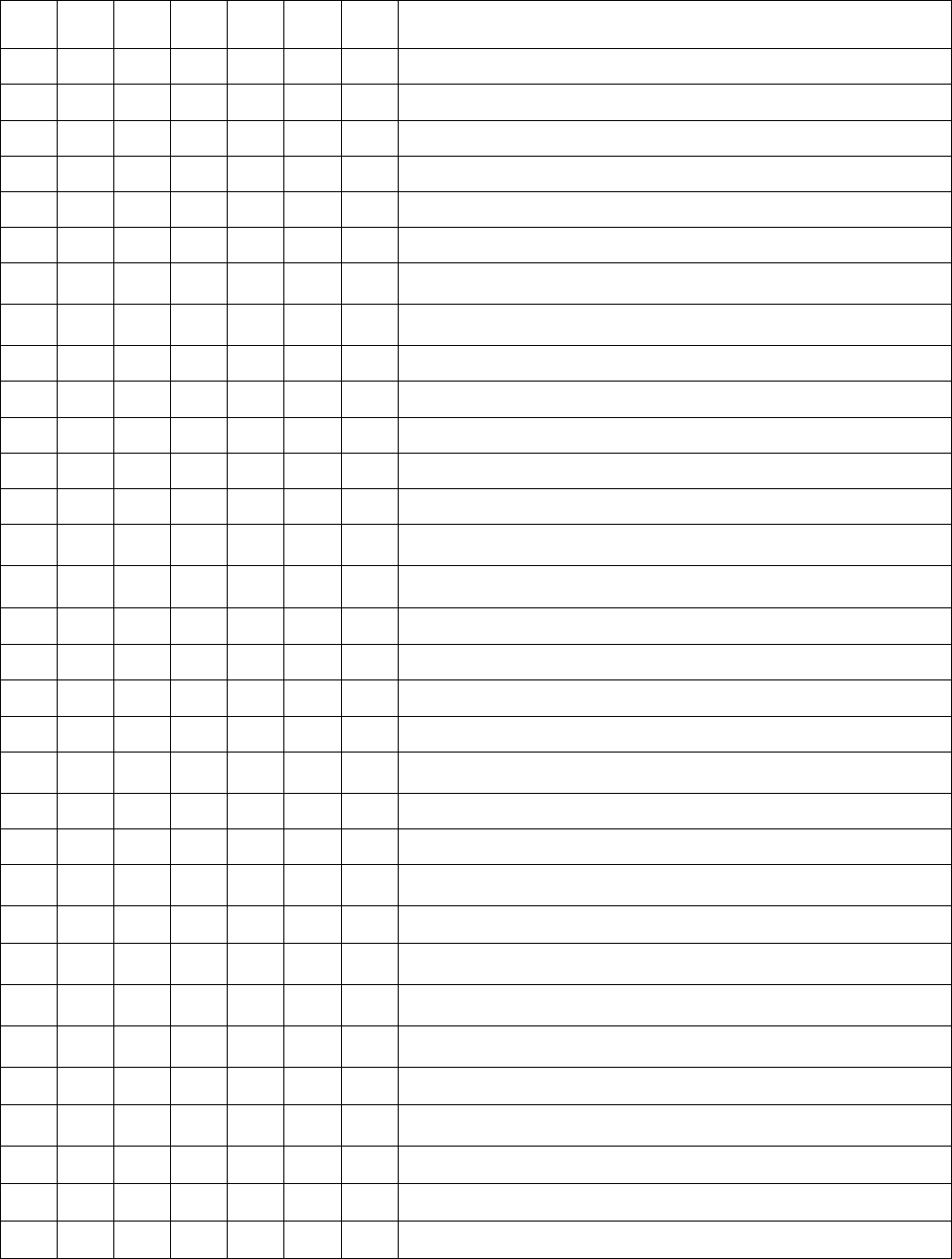
Таблица 5
Таблица состояния системы
14
№
1 2 3 4 5
Y P(Y
i
), Q(Y
i
)
0 0 0 0 0 0 0
1 0 0 0 0 1 0
2 0 0 0 1 0 0
3 0 0 0 1 1 0
4 0 0 1 0 0 0
5 0 0 1 0 1 0
6 0 0 1 1 0 1
5
10113910920938004400240
−
⋅=⋅⋅⋅⋅ ,,,,,,
7 0 0 1 1 1 1
4
10202890920938004400240
−
⋅=⋅⋅⋅⋅ ,,,,,,
8 0 1 0 0 0 0
9 0 1 0 0 1 0
10
0 1 0 1 0 0
11
0 1 0 1 1 0
12
0 1 1 0 0 0
13
0 1 1 0 1 1
3
1055190080938095600240
−
⋅=⋅⋅⋅⋅ ,,,,,,
14
0 1 1 1 0 1
3
100015210920938095600240
−
⋅=⋅⋅⋅⋅ ,,,,,,
15
0 1 1 1 1 1
01782090920938095600240 ,,,,,,
=
⋅
⋅
⋅
⋅
16
1 0 0 0 0 0
17
1 0 0 0 1 0
18
1 0 0 1 0 0
19
1 0 0 1 1 1
3
10205290920062004409760
−
⋅=⋅⋅⋅⋅ ,,,,,,
20
1 0 1 0 0 0
21
1 0 1 0 1 0
22
1 0 1 1 0 1
3
10706310920938004409760
−
⋅=⋅⋅⋅⋅ ,,,,,,
23
1 0 1 1 1 1
03335090920938004409760 ,,,,,,
=
⋅
⋅
⋅
⋅
24
1 1 0 0 0 1
4
1063410080062095609760
−
⋅=⋅⋅⋅⋅ ,,,,,,
25
1 1 0 0 1 1
3
101652490080062095609760
−
⋅=⋅⋅⋅⋅ ,,,,,,
26
1 1 0 1 0 1
3
1032510920062095609760
−
⋅=⋅⋅⋅⋅ ,,,,,,
27
1 1 0 1 1 1
079090920062095609760 ,,,,,,
=
⋅
⋅
⋅
⋅
28
1 1 1 0 0 1
3
1000710080938095609760
−
⋅=⋅⋅⋅⋅ ,,,,,,
29
1 1 1 0 1 1
063090080938095609760 ,,,,,,
=
⋅
⋅
⋅
⋅
30
1 1 1 1 0 1
081010920938095609760 ,,,,,,
=
⋅
⋅
⋅
⋅
31
1 1 1 1 1 1
7274090920938095609760
=
⋅
⋅
⋅
⋅
,,,,,
Таким образом, общая надежность безотказной работы всего изделия:
15
94230)1((1000) ,YPP
iобщ
=
=
=
.
Рассчитаем интенсивность отказа:
5
1094325
1000
94230
−
⋅=−=λ ,
,ln
1/ч.
Таким образом, функции надежности и ненадежности данной мостовой
схемы выглядят следующим образом:
t,
etP
⋅⋅−
−
=
5
1094325
)( ;
t,
etQ
⋅⋅−
−
−=
5
1094325
1)( .
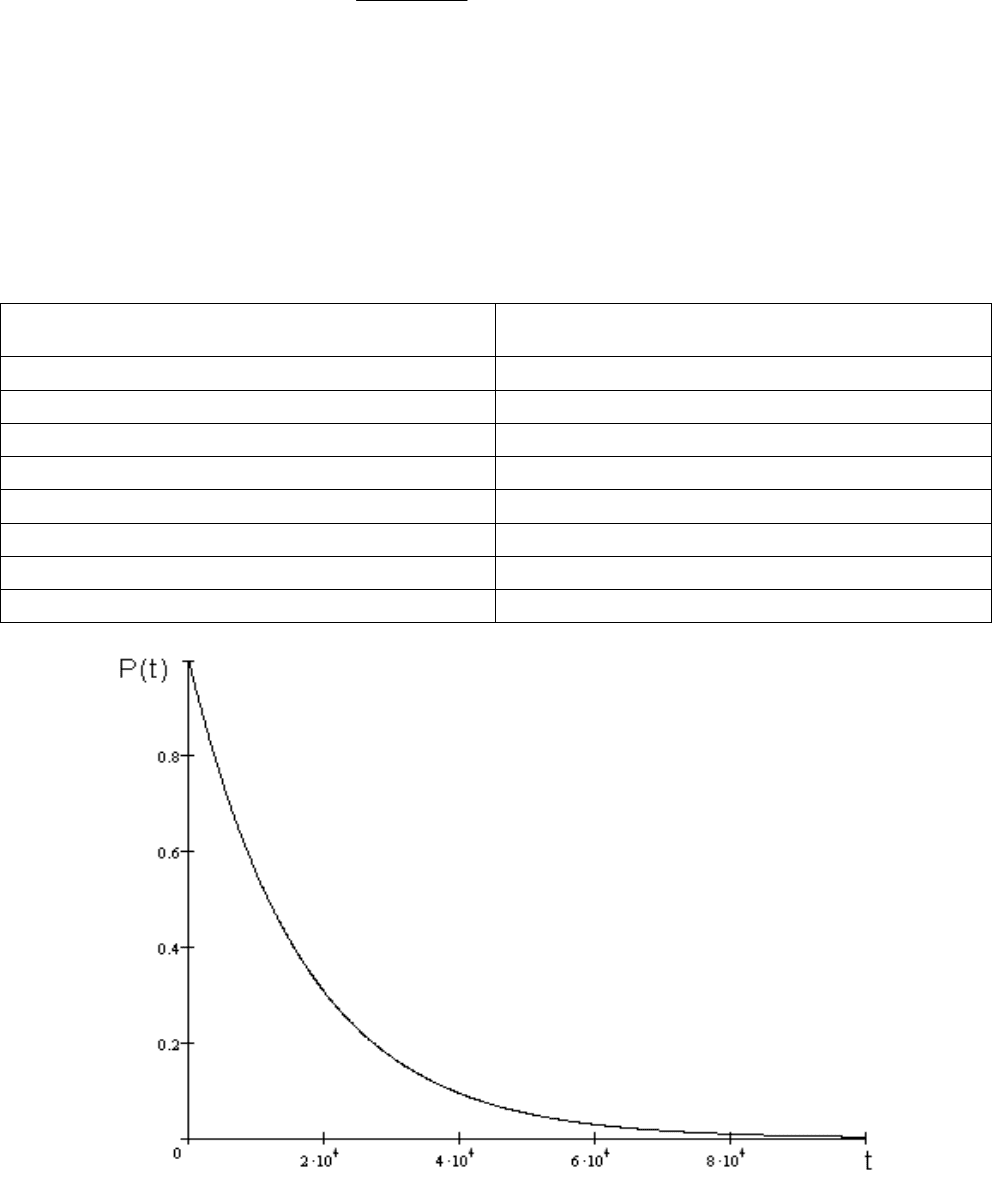
Построим их графически (рис. 7 и 8).
Таблица 6
Расчет функции надежности для различных значений t
t, час P(t)
1000 0,94229961
5000 0,742925
10000 0,551938
15000 0,41
18000 0,34309
20000 0,305
25000 0,226
30000 0,125
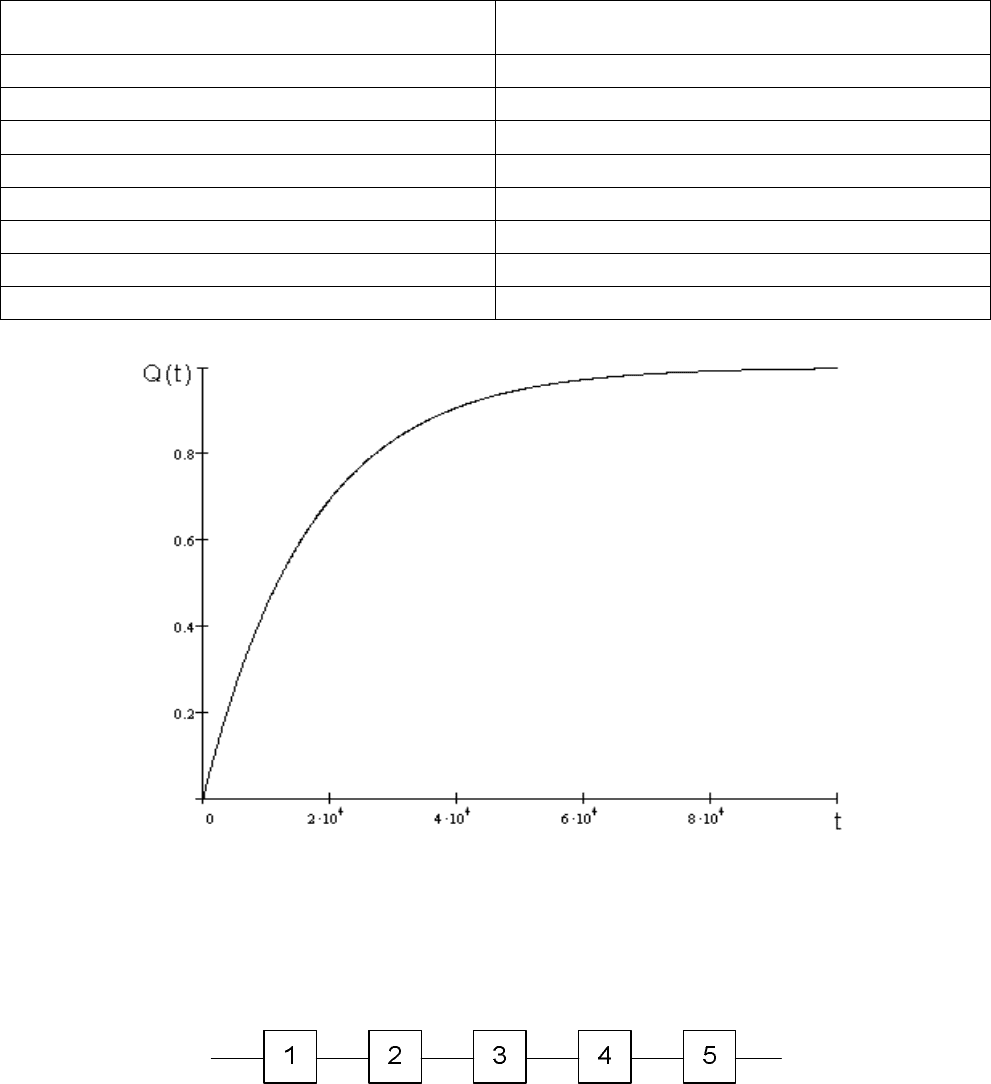
Рис. 7. Функция надежности
Таблица 7
16
Расчет функции ненадежности для различных значений t
t, час Q(t)
1000 0,0577
5000 0,257075
10000 0,4481
15000 0,59
18000 0,65691
20000 0,695
25000 0,774
35000 0,875
Рис. 8. Функция ненадежности
Для подтверждения основных выводов теории надежности приведем
расчет вероятности системы, состоящей из тех же элементов, включенных
последовательно (рис. 9).
Рис. 9. Структурная схема из пяти последовательно
соединенных элементов
Таким образом, общая надежность безотказной работы всего изделия
за время T = 1000 часов:
P(1000) = 0.976 ⋅ 0.956 ⋅ 0.938 ⋅ 0.92 ⋅ 0.9 = 0.7247.
И теоретически и практически метод, приведенный в данном расчете,

17
является универсальным. Он пригоден для расчета схем любой сложности
и конфигурации.
Очевидно при рассмотрении и сравнении мостовой и последователь-
ной схем, можно сказать, что надежность мостовой схемы значительно
превышает надежность последовательной схемы. А это, в первую оче-
редь, свидетельствует в пользу мостовой схемы, а также подтверждает
утверждение, приведенное в задании 1.
ЗАДАНИЕ 4
Под ЛПС (линейной переключательной схемой) понимается структур-
ная схема алгоритма, построенная на элементах задержки, правило со-
единения которых заключается в том, что любое число выходов любого
элемента может быть соединено с любым числом входов.
Различают четыре конфигурации алгоритмов:
– без обратной связи (ЛПС – А, ЛПС – В);
– с обратной связью (ЛПС – С, ЛПС – Д).
ЛПС – А и ЛПС – В осуществляют умножение входной последователь-
ности на некоторый характеристический полином h(x), ЛПС – С и ЛПС – Д
осуществляют деление входной последовательности на характеристиче-
ский полином h(x).
В задании предусмотрено исследование алгоритмов ЛПС – С и ЛПС –
Д. Требуется произвести анализ надежности реализации этих алгоритмов
и сравнить их. Каждой структуре соответствует характеристический поли-
ном восьмой степени.
Степень характеристического полинома соответствует числу элементов
задержки в схеме (8), а число сумматоров на единицу меньше числа нену-
левых членов этого полинома (4).
По заданию задаемся:
Порождающий полином:
h(x) =
1
568
+
+
+
+
x
x
x
x
.
Делимый полином:
1
568
++++=ρ xxxX)x( .
Представим соответствующую ЛПС – Д (со встроенными сумматорами)
(рис. 10.)
Рис. 10. Схема ЛПС – Д
Удобной формой представления этого алгоритма является таблица

18
действующих сигналов. Из этой таблицы можно определить для любого
действующего сигнала, сколько элементарных операций он претерпел.
Величина γ (t) – число шагов перехода, определяет сложность обработки
действующих сигналов. Автоматное реальное время измеряется в тактах.
Каждый элемент задержки в первом полутакте записывает информа-
цию, а во втором считывает. Таким образом, элементарными операциями
является запись и считывание. Исходя из вышесказанного, рассчитывает-
ся γ (t) в нижеприведенной таблице.
Таблица 8
Действующие сигналы ЛПС – Д
t
0 1 2 3 4 5 6 7 8 9 10 11 12
p(t)
– 1 0 1 1 0 0 0 1 1 – –
–
p(t)⊕
2
8
y
– 1 0 1 1 0 0 0 1 0 0 0 0
1
1
y
0 1 0 1 1 0 0 0 1 0 0 0 0
2
1
y
– 0 1 0 1 1 0 0 0 1 0 0 0
2
8
2
1
yy ⊕
– 0 1 0 1 1 0 0 0 1 0 0 0
1
2
y
0 0 1 0 1 1 0 0 0 1 0 0 0
2
2
y
– 0 0 1 0 1 1 0 0 0 1 0 0
1
3
y
0 0 0 1 0 1 1 0 0 0 1 0 0
2
3
y
– 0 0 0 1 0 1 1 0 0 0 1 0
1
4
y
0 0 0 0 1 0 1 1 0 0 0 1 0
2
4
y
– 0 0 0 0 1 0 1 1 0 0 0 1
1
5
y
0 0 0 0 0 1 0 1 1 0 0 0 1
2
5
y
– 0 0 0 0 0 1 0 1 1 0 0 0
2
8
2
5
yy ⊕
– 0 0 0 0 0 1 0 1 0 0 0 0
1
6
y
0 0 0 0 0 0 1 0 1 0 0 0 0
2
6
y
– 0 0 0 0 0 0 1 0 1 0 0 0
2
8
2
6
yy ⊕
– 0 0 0 0 0 0 1 0 0 0 0 0
Окончание табл. 8

19
t
0 1 2 3 4 5 6 7 8 9 10 11 12
1
7
y
0 0 0 0 0 0 0 1 0 0 0 0 0
2
7
y
– 0 0 0 0 0 0 0 1 0 0 0 0
1
8
y
0 0 0 0 0 0 0 0 1 0 0 0 0
2
8
y
– 0 0 0 0 0 0 0 0 1 0 0 0
Z(t) – 0 0 0 0 0 0 0 0 1 0 0 0
)(t
γ
– 1 3 6 11 18 28 42 62 90 129
185
264
Вероятности отсутствия и возникновения ошибки на каждом шаге пред-
ставлены в табл. 9 и рассчитываются по формулам:
t
,,tP
γ
λ−+=γ )21(5050)]([ ;
t
,,tQ
γ
λ−−=γ )21(5050)]([ ,
где λ – интенсивность отказов.
Таблица 9
Вероятности возникновения и отсутствия ошибки
t γ(t) P(t) Q(t)
0
– – –
1
1 0,999 0,001
2
3 0,997006 0,00299
3
6 0,994 0,00597
4
11 0,9891 0,0109
5
18 0,9823 0,0177
6
28 0,9727 0,0273
7
42 0,9597 0,0403
8
62 0,9416 0,0584
9
90 0,9176 0,0824
10
129 0,8862 0,1138
11
185 0,8452 0,1548
12
264 0,7947 0,2053
Далее приведен график зависимости вероятностей отсутствия и воз-
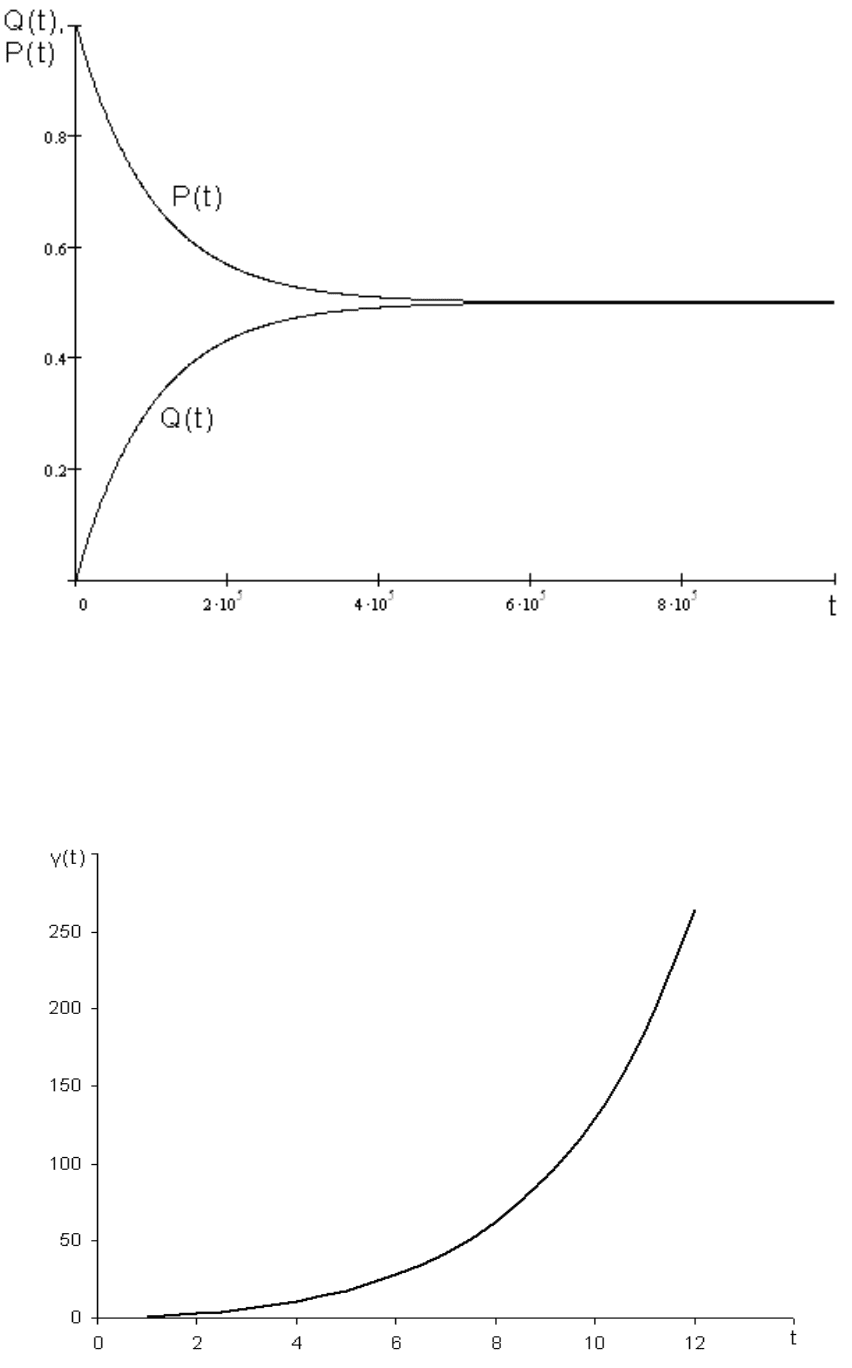
никновения ошибок для данной схемы от дискретного времени (рис. 11).
20
Рис. 11. Зависимость вероятностей отсутствия и возникновения ошибок
Из графика видно, что вероятность наличия и отсутствия ошибки стре-
миться к максимальной энтропии, то есть к 0,5.
Зависимость числа шагов перехода от дискретного времени представ-
лена на нижеприведенном графике (рис. 12).
Рис. 12. Зависимость количества возникающих ошибок от числа тактов
