Stone M., Goldbart P. Mathematics for Physics: A Guided Tour for Graduate Students
Подождите немного. Документ загружается.


10.3 Cartesian tensors 365
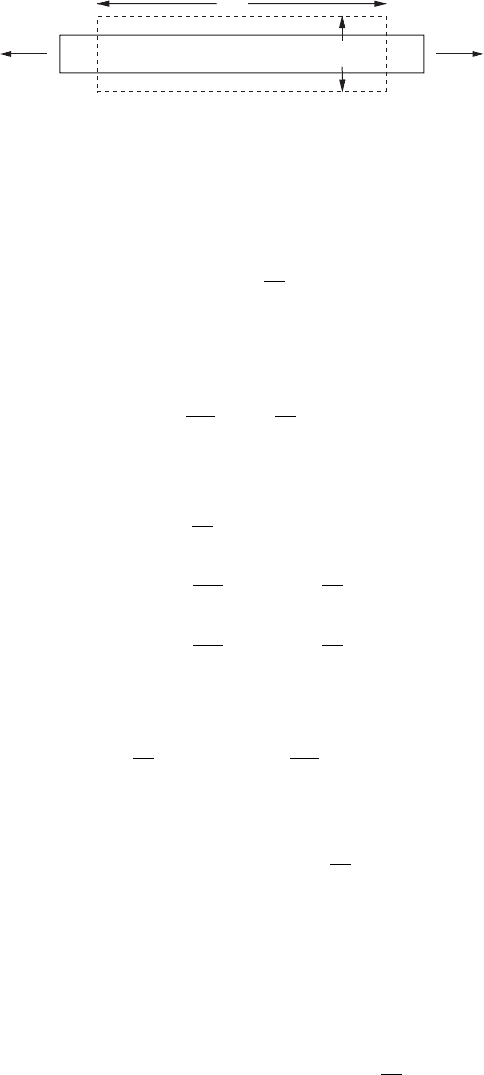
F
n
d| S|
Figure 10.1 Stress forces.
of the body scales to zero as
3
, but the forces are proprtional to the areas of the sides
and go to zero only as
2
. Only if the linear relation holds true can the acceleration of
the tetrahedron remain finite. A similar argument applied to torques and the moment of
inertia of a small cube shows that σ
ij
= σ
ji
.
A generalization of Hooke’s law,
σ
ij
= c
ijkl
e
kl
, (10.92)
relates the stress to the strain via the tensor of elastic constants c
ijkl
. This rank-four tensor
has the symmetry properties
c
ijkl
= c
klij
= c
jikl
= c
ijlk
. (10.93)
In other words, the tensor is symmetric under the interchange of the first and second
pairs of indices, and also under the interchange of the individual indices in either pair.
For an isotropic material – a material whose properties are invariant under the rotation
group SO(3) – the tensor of elastic constants must be an isotropic tensor. The most general
such tensor with the required symmetries is
c
ijkl
= λδ
ij
δ
kl
+ µ(δ
ik
δ
jl
+ δ
il
δ
jk
). (10.94)
An isotropic material is therefore characterized by only two independent parameters,
λ and µ. These are called the Lamé constants after the mathematical engineer Gabriel
Lamé. In terms of them the generalized Hooke’s law becomes
σ
ij
= λδ
ij
e
kk
+ 2µe
ij
. (10.95)
By considering particular deformations, we can express the more directly measurable
bulk modulus, shear modulus, Young’s modulus and Poisson’s ratio in terms of λ and µ.
The bulk modulus κ is defined by
dP =−κ
dV
V
, (10.96)

366 10 Vectors and tensors
where an infinitesimal isotropic external pressure dP causes a change V → V + dV
in the volume of the material. This applied pressure corresponds to a surface stress of
σ
ij
=−δ
ij
dP. An isotropic expansion displaces points in the material so that
η
i
=
1
3
dV
V
x
i
. (10.97)
The strains are therefore given by
e
ij
=
1
3
δ
ij
dV
V
. (10.98)
Inserting this strain into the stress–strain relation gives
σ
ij
= δ
ij
λ +
2
3
µ
dV
V
=−δ
ij
dP. (10.99)
Thus
κ = λ +
2
3
µ. (10.100)
To define the shear modulus, we assume a deformation η
1
= θx
2
,soe
12
= e
21
= θ/2,
with all other e
ij
vanishing (see Figure 10.2).
The applied shear stress is σ
12
= σ
21
. The shear modulus is defined to be σ
12
/θ.
Inserting the strain components into the stress–strain relation gives
σ
12
= µθ, (10.101)
and so the shear modulus is equal to the Lamé constant µ. We can therefore write the
generalized Hooke’s law as
σ
ij
= 2µ
e
ij
−
1
3
δ
ij
e
kk
+ κe
kk
δ
ij
, (10.102)
which reveals that the shear modulus is associated with the traceless part of the strain
tensor, and the bulk modulus with the trace.
21
12
12
21
Figure 10.2 Shear strain. The arrows show the direction of the applied stresses. The σ
21
on the
vertical faces are necessary to stop the body rotating.
10.3 Cartesian tensors 367
L
33
W
33
Figure 10.3 Forces on a stretched wire.
Young’s modulus Y is measured by stretching a wire of initial length L and square
cross-section of side W under a tension T = σ
33
W
2
.
We define Y so that
σ
33
= Y
dL
L
. (10.103)
At the same time as the wire stretches, its width changes W → W +dW . Poisson’s ratio
σ is defined by
dW
W
=−σ
dL
L
, (10.104)
so that σ is positive if the wire gets thinner as it gets longer. The displacements are
η
3
= z
dL
L
,
η
1
= x
dW
W
=−σ x
dL
L
,
η
2
= y
dW
W
=−σ y
dL
L
, (10.105)
so the strain components are
e
33
=
dL
L
, e
11
= e
22
=
dW
W
=−σ e
33
. (10.106)
We therefore have
σ
33
= (λ(1 − 2σ) + 2µ)
dL
L
, (10.107)
leading to
Y = λ(1 − 2σ)+ 2µ. (10.108)
Now, the side of the wire is a free surface with no forces acting on it, so
0 = σ
22
= σ
11
= (λ(1 − 2σ) − 2σµ)
dL
L
. (10.109)

368 10 Vectors and tensors
This tells us that
6
σ =
1
2
λ
λ + µ
, (10.110)
and
Y = µ
3λ + 2µ
λ + µ
. (10.111)
Other relations, following from those above, are
Y = 3κ(1 − 2σ),
= 2µ(1 + σ). (10.112)
Exercise 10.7: Show that the symmetries
c
ijkl
= c
klij
= c
jikl
= c
ijlk
imply that a general homogeneous material has 21 independent elastic constants. (This
result was originally obtained by George Green, of Green function fame.)
Exercise 10.8: A steel beam is forged so that its cross-section has the shape of a region
∈ R
2
. When undeformed, it lies along the z-axis. The centroid O of each cross-section
is defined so that
x dxdy =
y dxdy = 0,
when the coordinates x, y are taken with the centroid O as the origin. The beam is
slightly bent away from the z-axis so that the line of centroids remains in the yz-plane
(see Figure 10.4). At a particular cross-section with centroid O, the line of centroids has
radius of curvature R.
z
x
y
O
Figure 10.4 Bent beam.
6
Poisson and Cauchy erroneously believed that λ = µ, and hence that σ = 1/4.

10.3 Cartesian tensors 369
O
x
y
Figure 10.5 The original (dashed) and anticlastically deformed (full) cross-section.
Assume that the deformation in the vicinity of O is such that
η
x
=−
σ
R
xy ,
η
y
=
1
2R
σ(x
2
− y
2
) − z
2
,
η
z
=
1
R
yz.
Observe that for this assumed deformation, and for a positive Poisson ratio, the cross-
section deforms anticlastically – the sides bend up as the beam bends down. This is
shown in Figure 10.5.
Compute the strain tensor resulting from the assumed deformation, and show that its
only non-zero components are
e
xx
=−
σ
R
y , e
yy
=−
σ
R
y , e
zz
=
1
R
y .
Next, show that
σ
zz
=
Y
R
y ,
and that all other components of the stress tensor vanish (Figure 10.6). Deduce from this
vanishing that the assumed deformation satisfies the free-surface boundary condition,
and so is indeed the way the beam responds when it is bent by forces applied at its ends.
The work done in bending the beam
beam
1
2
e
ij
c
ijkl
e
kl
d
3
x
is stored as elastic energy. Show that for our bent rod this energy is equal to
YI
2
1
R
2
ds ≈
YI
2
(y
)
2
dz,
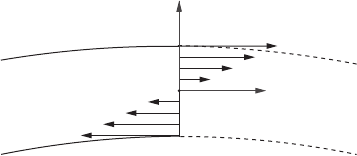
370 10 Vectors and tensors
y
z
Figure 10.6 The distribution of forces σ
zz
exerted on the left-hand part of the bent rod by the
material to its right.
where s is the arc-length taken along the line of centroids of the beam,
I =
y
2
dxdy
is the moment of inertia of the region about the x axis and y
denotes the second
derivative of the deflection of the beam with respect to z (which approximates the arc-
length). This last formula for the strain energy has been used in a number of our calculus
of variations problems.
10.3.3 Maxwell stress tensor
Consider a small cubical element of an elastic body. If the stress tensor were position
independent, the external forces on each pair of opposing faces of the cube would be
equal in magnitude but pointing in opposite directions. There would therefore be no net
external force on the cube. When σ
ij
is not constant then we claim that the total force
acting on an infinitesimal element of volume dV is
F
i
= ∂
j
σ
ij
dV . (10.113)
To see that this assertion is correct, consider a finite region with boundary ∂, and
use the divergence theorem to write the total force on as
F
tot
i
=
∂
σ
ij
n
j
d|S|=
∂
j
σ
ij
dV . (10.114)
Whenever the force-per-unit-volume f
i
acting on a body can be written in the form
f
i
= ∂
j
σ
ij
, we refer to σ
ij
as a “stress tensor”, by analogy with stress in an elastic solid.
As an example, let E and B be electric and magnetic fields. For simplicity, initially assume
them to be static. The force per unit volume exerted by these fields on a distribution of
charge ρ and current j is
f = ρE + j × B. (10.115)

10.3 Cartesian tensors 371
From Gauss’ law ρ = div D, and with D =
0
E, we find that the force per unit volume
due to the electric field has components
ρE
i
= (∂
j
D
j
)E
i
=
0
∂
j
(E
i
E
j
) − E
j
∂
j
E
i
=
0
∂
j
(E
i
E
j
) − E
j
∂
i
E
j
=
0
∂
j
E
i
E
j
−
1
2
δ
ij
|E|
2
. (10.116)
Here, in passing from the first line to the second, we have used the fact that curl E is
zero for static fields, and so ∂
j
E
i
= ∂
i
E
j
. Similarly, using j = curl H, together with
B = µ
0
H and div B = 0, we find that the force per unit volume due to the magnetic
field has components
(j × B)
i
= µ
0
∂
j
H
i
H
j
−
1
2
δ
ij
|H |
2
. (10.117)
The quantity
σ
ij
=
0
E
i
E
j
−
1
2
δ
ij
|E|
2
+ µ
0
H
i
H
j
−
1
2
δ
ij
|H |
2
(10.118)
is called the Maxwell stress tensor. Its utility lies in the fact that the total electromagnetic
force on an isolated body is the integral of the Maxwell stress over its surface. We do
not need to know the fields within the body.
Michael Faraday was the first to intuit a picture of electromagnetic stresses and
attributed both a longitudinal tension and a mutual lateral repulsion to the field lines.
Maxwell’s tensor expresses this idea mathematically.
Exercise 10.9: Allow the fields in the preceding calculation to be time dependent. Show
that Maxwell’s equations
curl E =−
∂B
∂t
, div B = 0,
curl H = j +
∂D
∂t
, div D = ρ,
with B = µ
0
H, D =
0
E and c = 1/
√
µ
0
0
, lead to
(ρE + j × B)
i
+
∂
∂t
1
c
2
(E × H)
i
= ∂
j
σ
ij
.
The left-hand side is the time rate of change of the mechanical (first term) and
electromagnetic (second term) momentum density. Observe that we can equivalently
write
∂
∂t
1
c
2
(E × H)
i
+ ∂
j
(−σ
ij
) =−(ρE + j × B)
i
,

372 10 Vectors and tensors
and think of this as a local field-momentum conservation law. In this interpretation −σ
ij
is thought of as the momentum flux tensor, its entries being the flux in direction j of the
component of field momentum in direction i. The term on the right-hand side is the rate
at which momentum is being supplied to the electromagnetic field by the charges and
currents.
10.4 Further exercises and problems
Exercise 10.10: Quotient theorem. Suppose that you have come up with some recipe for
generating an array of numbers T
ijk
in any coordinate frame, and want to know whether
these numbers are the components of a triply contravariant tensor. Suppose further that
you know that, given the components a
ij
of an arbitrary doubly covariant tensor, the
numbers
T
ijk
a
jk
= v
i
transform as the components of a contravariant vector. Show that T
ijk
does indeed
transform as a triply contravariant tensor. (The natural generalization of this result to
arbitrary tensor types is known as the quotient theorem.)
Exercise 10.11: Let T
i
j
be the 3-by-3 array of components of a tensor. Show that the
quantities
a = T
i
i
, b = T
i
j
T
j
i
, c = T
i
j
T
j
k
T
k
i
are invariant. Further show that the eigenvalues of the linear map represented by the
matrix T
i
j
can be found by solving the cubic equation
λ
3
− aλ
2
+
1
2
(a
2
− b)λ −
1
6
(a
3
− 3ab + 2c) = 0.
Exercise 10.12: Let the covariant tensor R
ijkl
possess the following symmetries:
(i) R
ijkl
=−R
jikl
,
(ii) R
ijkl
=−R
ijlk
,
(iii) R
ijkl
+ R
iklj
+ R
iljk
= 0.
Use the properties (i), (ii), (iii) to show that:
(a) R
ijkl
= R
klij
.
(b) If R
ijkl
x
i
y
j
x
k
y
l
= 0 for all vectors x
i
, y
i
, then R
ijkl
= 0.
(c) If B
ij
is a symmetric covariant tensor and we set A
ijkl
= B
ik
B
jl
− B
il
B
jk
, then A
ijkl
has the same symmetries as R
ijkl
.
Exercise 10.13: Write out Euler’s equation for fluid motion
˙v + (v ·∇)v =−∇h

10.4 Further exercises and problems 373
in cartesian tensor notation. Transform it into
˙v − v × ω =−∇
1
2
v
2
+ h
,
where ω =∇×v is the vorticity. Deduce Bernoulli’s theorem, that for steady (˙v = 0)
flow the quantity
1
2
v
2
+ h is constant along streamlines.
Exercise 10.14: The elastic properties of an infinite homogeneous and isotropic solid of
density ρ are described by Lamé constants λ and µ. Show that the equation of motion
for small-amplitude vibrations is
ρ
∂
2
η
i
∂t
2
= (λ + µ)
∂
2
η
j
∂x
i
∂x
j
+ µ
∂
2
η
i
∂x
2
j
.
Here η
i
are the cartesian components of the displacement vector η(x, t) of the particle
initially at the point x. Seek plane-wave solutions of the form
η = a exp{ik · x − iωt},
and deduce that there are two possible types of wave: longitudinal “P-waves”, which
have phase velocity
v
P
=
λ + 2µ
ρ
,
and transverse “S-waves”, which have phase velocity
v
S
=
<
µ
ρ
.
Exercise 10.15: Symmetric integration. Show that the n-dimensional integral
I
αβγ δ
=
d
n
k
(2π)
n
(k
α
k
β
k
γ
k
δ
) f (k
2
),
is equal to
A(δ
αβ
δ
γδ
+ δ
αγ
δ
βδ
+ δ
αδ
δ
βγ
),
where
A =
1
n(n + 2)
d
n
k
(2π)
n
(k
2
)
2
f (k
2
).

374 10 Vectors and tensors
Similarly evaluate
I
αβγ δ
=
d
n
k
(2π)
n
(k
α
k
β
k
γ
k
δ
k
) f (k
2
).
Exercise 10.16: Write down the most general three-dimensional isotropic tensors of rank
two and three.
In piezoelectric materials, the application of an electric field E
i
induces a mechanical
strain that is described by a rank-two symmetric tensor
e
ij
= d
ijk
E
k
,
where d
ijk
is a third-rank tensor that depends only on the material. Show that e
ij
can only
be non-zero in an anisotropic material.
Exercise 10.17: In three dimensions, a rank-five isotropic tensor T
ijklm
is a linear combi-
nation of expressions of the form
i
1
i
2
i
3
δ
i
4
i
5
for some assignment of the indices i, j, k, l, m
to the i
1
, ..., i
5
. Show that, on taking into account the symmetries of the Kronecker and
Levi-Civita symbols, we can construct ten distinct products
i
1
i
2
i
3
δ
i
4
i
5
. Only six of these
are linearly independent, however. Show, for example, that
ijk
δ
lm
−
jkl
δ
im
+
kli
δ
jm
−
lij
δ
km
= 0,
and find the three other independent relations of this sort.
7
(Hint: begin by showing that, in three dimensions,
δ
i
1
i
2
i
3
i
4
i
5
i
6
i
7
i
8
def
=
!
!
!
!
!
!
!
!
δ
i
1
i
5
δ
i
1
i
6
δ
i
1
i
7
δ
i
1
i
8
δ
i
2
i
5
δ
i
2
i
6
δ
i
2
i
7
δ
i
2
i
8
δ
i
3
i
5
δ
i
3
i
6
δ
i
3
i
7
δ
i
3
i
8
δ
i
4
i
5
δ
i
4
i
6
δ
i
4
i
7
δ
i
4
i
8
!
!
!
!
!
!
!
!
= 0,
and contract with
i
6
i
7
i
8
.)
Problem 10.18 : The Plücker relations. This problem provides a challenging test of your
understanding of linear algebra. It leads you through the task of deriving the necessary
and sufficient conditions for
A = A
i
1
...i
k
e
i
1
∧ ...∧ e
i
k
∈
@
k
V
to be decomposable as
A = f
1
∧ f
2
∧ ...∧ f
k
.
The trick is to introduce two subspaces of V ,
7
Such relations are called syzygies. A recipe for constructing linearly independent basis sets of isotropic
tensors can be found in: G. F. Smith, Tensor, 19 (1968) 79.
