Stone M., Goldbart P. Mathematics for Physics: A Guided Tour for Graduate Students

Подождите немного. Документ загружается.

9.7 Some functional analysis 335

so g is Hilbert–Schmidt and therefore the kernel of a compact operator. The eigenvalue

problem

= λ

(9.139)

can be recast as the integral equation



−1

g(x, x



) dx



(9.140)

with µ

= λ

−1

. The compactness of g guarantees that there is a complete set of eigen-

functions (these being the Legendre polynomials P

(x) for n > 0) having eigenvalues

= 1/n(n +1). The operator g also has the eigenfunction P

with eigenvalue µ

= 0.

This example provides the justification for the claim that the “finite” boundary conditions

we adopted for the Legendre equation in Chapter 8 give us a self-adjoint operator.

Note that K(x, y) does not have to be bounded for K to be Hilbert–Schmidt.

Example: The kernel

K(x, y) =

(x − y)

, |x|, |y| < 1 (9.141)

is Hilbert–Schmidt provided α<

Example: The kernel

K(x, y) =

−m|x−y|

, x, y ∈ R (9.142)

is not Hilbert–Schmidt because |K(x −y)| is constant along the lines x − y = constant,

which lie parallel to the diagonal. K has a continuous spectrum consisting of all positive

real numbers less than 1/m

. It cannot be compact, therefore, but it is bounded with

K=1/m

. The integral equation (9.22) contains this kernel, and the Fredholm

alternative does not apply to it.

9.7.2 Closed operators

One motivation for our including a brief account of functional analysis is that an attentive

reader will have realized that some of the statements we have made in earlier chapters

appear to be inconsistent. We have asserted in Chapter 2 that no significance can be

attached to the value of an L

function at any particular point – only integrated averages

matter. In later chapters, though, we have happily imposed boundary conditions that

require these very functions to take specified values at the endpoints of our interval.

In this section we will resolve this paradox. The apparent contradiction is intimately

connected with our imposing boundary conditions only on derivatives of lower order

336 9 Integral equations

than that of the differential equation, but understanding why this is so requires some

function-analytic language.

Differential operators L are never continuous; we cannot deduce from u

→ u that

→ Lu. Differential operators can be closed, however. A closed operator is one for

which whenever a sequence u

converges to a limit u and at the same time the image

sequence Lu

also converges to a limit f , then u is in the domain of L and Lu = f . The

name is not meant to imply that the domain of definition is closed, but indicates instead

that the graph of L – this being the set {u, Lu}considered as a subset of L

[a, b]×L

[a, b]

– contains its limit points and so is a closed set.

Any self-adjoint operator is automatically closed. To see why this is so, recall that in

defining the adjoint of an operator A, we say that y is in the domain of A

†

if there is a z

such that y, Ax=z, x for all x in the domain of A. We then set A

†

y = z. Now suppose

that y

→ y and A

†

= z

→ z. The Cauchy–Schwartz–Bunyakovski inequality shows

that the inner product is a continuous function of its arguments. Consequently, if x is

in the domain of A, we can take the limit of y

, Ax=A

†

, x=z

, x to deduce

that y, Ax=z, x. But this means that y is in the domain of A

†

, and z = A

†

y . The

adjoint of any operator is therefore a closed operator. A self-adjoint operator, being its

own adjoint, is therefore necessarily closed.

A deep result states that a closed operator defined on a closed domain is bounded.

Since they are always unbounded, the domain of a closed differential operator can never

be a closed set.

An operator may not be closed but may be closable, in that we can make it closed by

including additional functions in its domain. The essential requirement for closability is

that we never have two sequences u

and v

which converge to the same limit, w, while

and Lv

both converge, but to different limits. Closability is equivalent to requiring

that if u

→ 0 and Lu

converges, then Lu

converges to zero.

Example: Let L = d/dx. Suppose that u

→ 0 and Lu

→ f .Ifϕ is a smooth L

function

that vanishes at 0, 1, then



ϕfdx= lim

n→∞



dx =−lim

n→∞





dx = 0. (9.143)

Here we have used the continuity of the inner product to justify the interchange of the

order of limit and integral. By the same arguments we used when dealing with the

calculus of variations, we deduce that f = 0. Thus d/dx is closable.

If an operator is closable, we may as well add the extra functions to its domain and

make it closed. Let us consider what closure means for the operator

L =

, D(L) ={y ∈ C

[0, 1] : y



(0) = 0}. (9.144)

Here, in fixing the derivative at the endpoint, we are imposing a boundary condition of

higher order than we ought.

9.7 Some functional analysis 337

Figure 9.10 lim

a→0

= y in L

[0, 1] .



y

Figure 9.11 y



→ y



in L

[0, 1] .

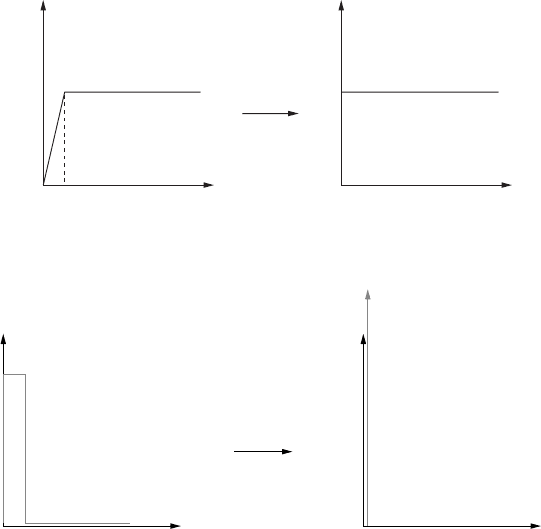
Consider the sequence of differentiable functions y

shown in Figure 9.10. These

functions have vanishing derivative at x = 0, but tend in L

to a function y whose

derivative is non-zero at x = 0.

Figure 9.11 shows that the derivative of these functions also converges in L

If we want L to be closed, we should therefore extend the domain of definition of L to

include functions with non-vanishing endpoint derivative. We can also use this method

to add to the domain of L functions that are only piecewise differentiable – i.e. functions

with a discontinuous derivative.

Now consider what happens if we try to extend the domain of

L =

, D(L) ={y, y



∈ L

: y(0) = 0}, (9.145)

to include functions that do not vanish at the endpoint. Take the sequence of functions

shown in Figure 9.12. These functions vanish at the origin, and converge in L

to a

function that does not vanish at the origin.

Now, as Figure 9.13 shows, the derivatives converge towards the derivative of the limit

function – together with a delta function near the origin. The area under the functions



(x)|

grows without bound and the sequence Ly

becomes infinitely far from the

derivative of the limit function when distance is measured in the L

norm.

338 9 Integral equations

Figure 9.12 lim

a→0

= y in L

[0, 1].

1/a



␦

(

)

Figure 9.13 y



→ δ(x), but the delta function is not an element of L

[0, 1].

We therefore cannot use closure to extend the domain to include these functions.

Another way of saying this is that in order for the weak derivative of y to be in L

and therefore for y to be in the domain of d/dx, the function y need not be classically

differentiable, but its L

equivalence class must contain a continuous function – and

continuous functions do have well-defined values. It is the values of this continuous

representative that are constrained by the boundary conditions.

This story repeats for differential operators of any order: if we try to impose boundary

conditions of too high an order, they are washed out in the process of closing the operator.

Boundary conditions of lower order cannot be eliminated, however, and so make sense

as statements involving functions in L

9.8 Series solutions

One of the advantages of recasting a problem as an integral equation is that the equation

often suggests a systematic approximation scheme. Usually we start from the solution

of an exactly solvable problem and expand the desired solution about it as an infinite

series in some small parameter. The terms in such a perturbation series may become

9.8 Series solutions 339

progressively harder to evaluate, but, if we are lucky, the sum of the first few will prove

adaquate for our purposes.

9.8.1 Liouville–Neumann–Born series

The geometric series

S = 1 − x + x

− x

+··· (9.146)

converges to 1/(1 + x) provided |x| < 1. Suppose we wish to solve

(I + λK)ϕ = f (9.147)

where K is an integral operator. It is then natural to write

ϕ = (I + λK)

−1

f = (1 − λK + λ

− λ

+···)f , (9.148)

where

(x, y) =



K(x, z )K (z, y) dz ,

(x, y) =



K(x, z

)K(z

, z

)K(z

, y) dz

, (9.149)

and so on. This Liouville–Neumann series will converge, and yield a solution to the

problem, provided that λK < 1. In quantum mechanics this series is known as the

Born series.

9.8.2 Fredholm series

A familiar result from high-school algebra is Cramer’s rule, which gives the solution of

a set of linear equations in terms of ratios of determinants. For example, the system of

equations

+ a

= b

+ a

= b

+ a

= b

, (9.150)

has solution

, x

(9.151)

340 9 Integral equations

where

D =

. (9.152)

Although not as computationally efficient as standard Gaussian elimination, Cramer’s

rule is useful in that it is a closed-form solution. It is equivalent to the statement that

the inverse of a matrix is given by the transposed matrix of the cofactors, divided by the

determinant.

A similar formula for integral equations was given by Fredholm. The equations he

considered were, in operator form,

(I + λK)ϕ = f , (9.153)

where I is the identity operator, K is an integral operator with kernel K(x, y) and λ a

parameter. We motivate Fredholm’s formula by giving an expansion for the determinant

of a finite matrix. Let K be an n-by-n matrix

D(λ)

def

= det (I + λK) ≡

1 + λK

λK

··· λK

λK

1 + λK

··· λK

λK

··· 1 + λK

. (9.154)

Then

D(λ) =



m=0

, (9.155)

where A

= 1, A

= tr K ≡



, A



. (9.156)

The pattern for the rest of the terms should be obvious, as should the proof.

As observed above, the inverse of a matrix is the reciprocal of the determinant of the

matrix multiplied by the transposed matrix of the cofactors. So, if D

µν

is the cofactor of

the term in D(λ) associated with K

νµ

, then the solution of the matrix equation

(I + λK)x = b (9.157)

µ1

+ D

µ2

+···+D

µn

D(λ)

. (9.158)

9.8 Series solutions 341

If µ = ν we have

µν

= λK

µν

+ λ



µν

µi

iν

+ λ



µν

µi

+··· (9.159)

When µ = ν we have

µν

= δ

µν

;

D(λ), (9.160)

where

;

D(λ) is the expression analogous to D(λ), but with the µ-th row and column

deleted.

These elementary results suggest the definition of the Fredholm determinant of the

integral kernel K(x, y), a < x, y < b,as

D(λ) = Det |I + λK|≡

∞



m=0

, (9.161)

where A

= 1, A

= Tr K ≡



K(x, x) dx,



K(x

, x

) K(x

, x

)

K(x

, x

) K(x

, x

)



K(x

, x

) K(x

, x

) K(x

, x

)

K(x

, x

) K(x

, x

) K(x

, x

)

K(x

, x

) K(x

, x

) K(x

, x

)

, (9.162)

etc. We also define

D(x, y, λ) = λK(x, y) + λ



K(x, y) K(x, ξ)

K(ξ, y) K(ξ , ξ)

dξ

+ λ



K(x, y) K(x, ξ

) K(x, ξ

)

K(ξ

, y) K(ξ

, ξ

) K(ξ

, ξ

)

K(ξ

, y) K(ξ

, ξ

) K(ξ

, ξ

)

dξ

+···,

(9.163)

and then

ϕ(x) = f (x) +

D(λ)



D(x, y, λ)f (y) dy (9.164)

is the solution of the equation

ϕ(x) + λ



K(x, y)ϕ(y) dy = f (x). (9.165)

342 9 Integral equations

If |K(x, y)| < M in [a, b]×[a, b], the Fredholm series for D(λ) and D(x, y, λ) converge

for all λ, and define entire functions. In this feature it is unlike the Neumann series,

which has a finite radius of convergence.

The proof of these claims follows from the identity

D(x, y, λ) + λD(λ)K(x, y) + λ



D(x, ξ , λ)K (ξ , y) dξ = 0, (9.166)

or, more compactly with G(x, y) = D(x, y, λ)/D(λ),

(I + G)(I + λK) = I . (9.167)

For details see Whitaker and Watson §11.2.

Example: The equation

ϕ(x) = x + λ



xy ϕ(y) dy (9.168)

gives us

D(λ) = 1 −

λ, D(x, y, λ) = λxy (9.169)

and so

ϕ(x) =

3 − λ

. (9.170)

(We have considered this equation and solution before, in Section 9.4.)

9.9 Further exercises and problems

Exercise 9.1: The following problems should be relatively easy.

(a) Solve the inhomogeneous Type II Fredholm integral equation

u(x ) = e

+ λ



xy u(y) dy .

(b) Solve the homogeneous Type II Fredholm integral equation

u(x ) = λ



sin(x − y ) u(y) dy .

u(x ) = x + λ



(yx + y

) u(y) dy

to second order in λ using

9.9 Further exercises and problems 343

(i) the Neumann series; and

(ii) the Fredholm series.

(d) By differentiating, solve the integral equation: u(x) = x +



u(y) dy.

(e) Solve the integral equation: u(x) = x



xy u(y) dy.

(f) Find the eigenfunction(s) and eigenvalue(s) of the integral equation

u(x ) = λ



x−y

u(y) dy .

(g) Solve the integral equation: u(x) = e

+ λ



x−y

u(y) dy.

(h) Solve the integral equation

u(x ) = x +



dy (1 + xy) u(y)

for the unknown function u(x).

Exercise 9.2: Solve the integral equation

u(x ) = f (x) + λ



u(y)dy,0< x < 1

for the unknown u(x) in terms of the given function f (x). For what values of λ does a

unique solution u(x) exist without restrictions on f (x)? For what value λ = λ

does a

solution exist only if f (x) satisfies some condition? Using the language of the Fredholm

alternative, and the range and null-space of the relevant operators, explain what is

happening when λ = λ

. For the case λ = λ

find explicitly the condition on f (x)

and, assuming this condition is satisfied, write down the corresponding general solution

for u(x). Check that this solution does indeed satisfy the integral equation.

Exercise 9.3: Use a Laplace transform to find the solution to the generalized Abel

equation

f (x) =



(x − t)

−µ

u(t)dt,0<µ<1,

where f (x) is given and f (0) = 0. Your solution will be of the form

u(x ) =



K(x − t)f



(t)dt,

and you should give an explicit expression for the kernel K(x − t).

You will find the formula



∞

µ−1

−pt

dt = p

−µ

(µ), µ>0

to be useful.

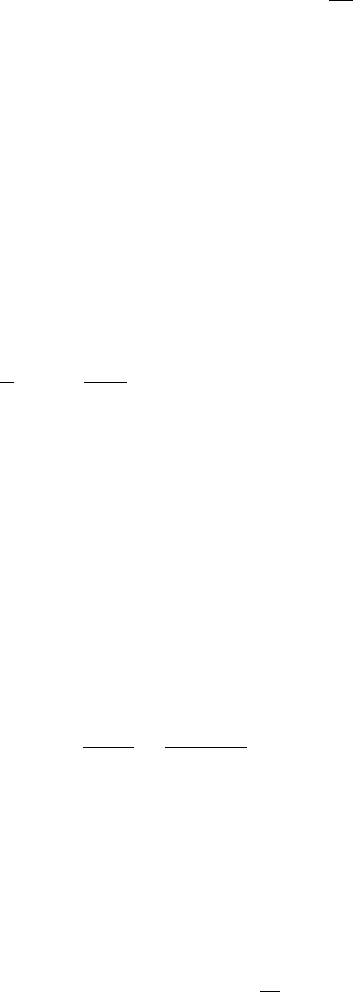
344 9 Integral equations

Exercise 9.4: Translationally invariant kernels.

(a) Consider the integral equation: u(x) = g(x) +λ



∞

−∞

K(x, y) u (y) dy, with the trans-

lationally invariant kernel K(x, y) = Q(x −y), in which g, λ and Q are known. Show

that the Fourier transforms ˆu, ˆg and

Q satisfy ˆu(q) =ˆg(q)/{1−

√

2πλ

Q(q)}. Expand

this result to second order in λ to recover the second-order Liouville–Neumann–Born

series.

(b) Use Fourier transforms to find a solution of the integral equation

u(x ) = e

−|x|

+ λ



∞

−∞

−|x−y|

u(y) dy

that remains finite as |x|→∞.

u(x ) = e

−x

+ λ



−|x−y|

u(y) dy x > 0.

Exercise 9.5: The integral equation



∞

φ(y)

x + y

= f (x), x > 0,

relates the unknown function φ to the known function f .

(i) Show that the changes of variables

x = exp 2ξ , y = exp 2η,

φ(exp 2η) exp η = ψ(η), f (exp 2ξ) exp ξ = g(ξ ),

convert the integral equation into one that can be solved by an integral transform.

(ii) Hence, or otherwise, construct an explicit formula for φ(x) in terms of a double

integral involving f (y).

You may use without proof the integral



∞

−∞

dξ

−isξ

cosh ξ

cosh πs/2

Exercise 9.6: Using Mellin transforms. Recall that the Mellin transform

;

f (s) of the

function f (t) is defined by

;

f (s) =



∞

dt t

s−1

f (t) .

(a) Given two functions, f (t) and g(t), a Mellin convolution f ∗g can be defined through

(f ∗ g)(t) =



∞

f (tu

−1

) g(u)