Stevenson J. Power system analysis
Подождите немного. Документ загружается.

686
CHAPTER 15 ATE ESTIMATION OF POWER SYSTEMS
GU 15.6
.
�
®
P31
I
! t
Q
3
1 P3
2
Q32
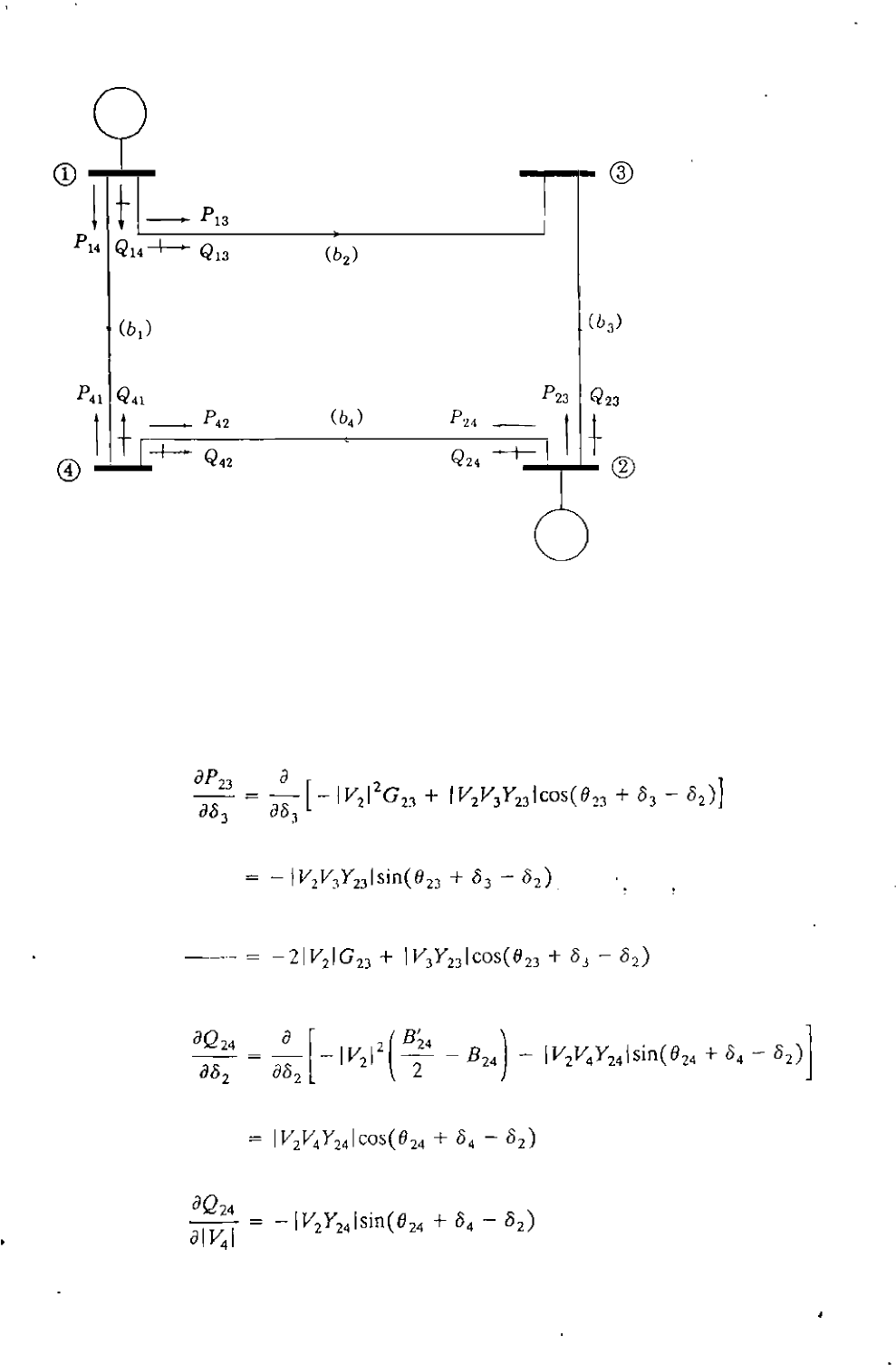
One-line diagram for Example 15.8 showing the ?ij and Qij measurements on lines marked b1
to b4•
The expressions for a
P
n/a8
3
' ap2
3
/al V2 1, a
Q
2
4
/ao
2
' and
a
Q2
4/al
V
41 are given by
Table 15.5 as follows:
JP23
a\V21
The expressions for other elements can be similarly obtained.

15.6 SUM
RY 7
A state-estimation algorithm based on measurements of only line ows
and the required bus-voltage magnitude is described in the literature to which
the reader is referred for further details.4
Because Hx has many zeros, the gain matrix G
x
= H�R -\ H x also has
many zeros, and so Gx is never explicitly inverted as implied by Eq. (15.60).
Instead LDU triangular factorization (described in Chap. 7), along with P -8
and Q -I
VI
decoupling (described in Sec. 9.7), and optimal ordering (de
scribed in Sec. B.1 of the Appendix) can be applied for ecient computations
and enhanced solution times of state estimation.
15.6 SUMMY
State estimation determines the existing operating conditions of the system
which are required for real-time control. The network model normally used
covers the transmission portion of the operating area. Hence, the parameter
values for all transmission Jines, transformers, capacitor banks, and intercon nec
tions are required as in power-ow studies. In this chapter it is assumed that
accurate parameters are known and on this basis state-estimation calculations
employing the basic weighted least-squares approach are described. The state
estimates are the bus-voltage angles and magnitudes which are computed by Eq.
(15.62) from a set of redundant measurements. When bad measurements are
detected, the state estimates are no longer reliable, which means that grossly
erroneous data have to be identied and ltered out by statistical tests. The
diagonal elements of the covariance matrix R' = R - H
x
G; 1 H� are used to
calculate the largest standardized residuals which help in identiing the bad
measurements.
In industry studies most of the computation time is spent in evaluating the
gain matrix G
x
=
H�R -) Hx, which is very large, is symmetric, and contains
many zeros (very sparse). Because of its sparse nature, G
x
is not explicitly
inverted. Instead, optimal ordering and LDU factorization are employed. Con
vergence upon the solution of Eq. (15.62) can be inuenced by where the meters
are placed on the system and the types of measurements (whether injections,
voltage magnitudes, or line ows). Redundancy is important but a full set of
measurements is not necessary and may not be desirable from the computa
tional viewpoint.
41. F. Dopazo, O. A. Klitin, G. W. Stagg, and L. S. Van Slyck, "State Calculation of Power Systems
from Line Flow Measurements," IEEE T
- 2008 — 2025 «СтудМед»
