Stevenson J. Power system analysis
Подождите немного. Документ загружается.

6
. CHAER 15 STATE ESTIMATION OF POWER SYSTEMS
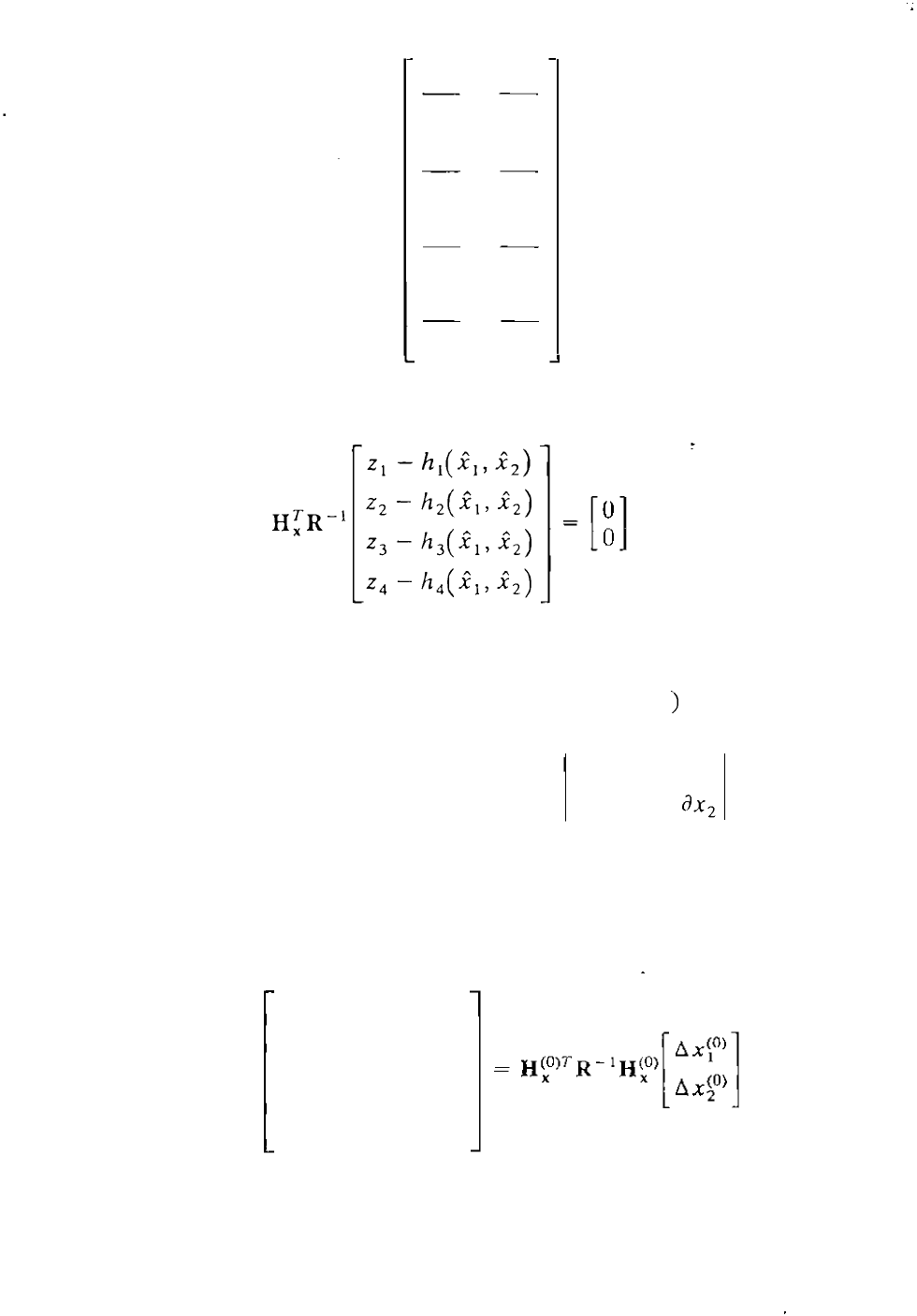
Noting that the partial derivative terms depend on x 1 and x2• let us dene
ah1
ah1
ax]
aX2
ah2
ah2
ax( aX
2
(15.56)
H =
ah3
ah3
x
ax (
aX2
Aiz
4
Ah4
Ax ]
AX2
and then we can write Eq. (15.55) in the more compact form
(15.57)
To solve this equation for the state estimates x 1 and X
2
, we follow the same
procedure as for the Newton-Raphson power ow. For example, using Eq.
(9.31) to linearize h/xl, x2) about the initial point (x�O), x�O» gives
ah (0
)
ah
(
0
)
h
(
x x
)
=
h
(
x
(
O
)
x
(
O
»
)
+
�
X
(
O
)_1 +
�
X
(
O)
_I
] I'
2
I I'
2
1
a
2
X
l
uX2
(1
5.58
)
whe
re, as before, x)O) = x�l) - x;O) represents the pical state-variable correc
tion and X)
I
) is the rst calculated value of Xi' Similarly, expanding hlx
I
' x
2
),
h3(x!, x2)
, and h/xl >
X
2)
; substituting the expansions in Eq. (15.57); and
rearranging yield
2
1
- h
l(
x
i°>'
x
�
O
»)
2
2
-h2(X�O\ x�O»)
H
(
O)
T
R
-
I
x
23 - h3(X�O), x&O»)
24
- h4( x�O), x�O»)
(15.59)
in which all quantities with the superscript (0) are computed at the initial values
x�O) and
x�O)
. We require the corrections �x 1 and X
2
to be (approximately)
zero in order to satis Eq. (15.57), and so the calculations of Eq. (15.59) are
continued by using X�k)
=
X�k
+
I
) - X�k) to form the more general iterative
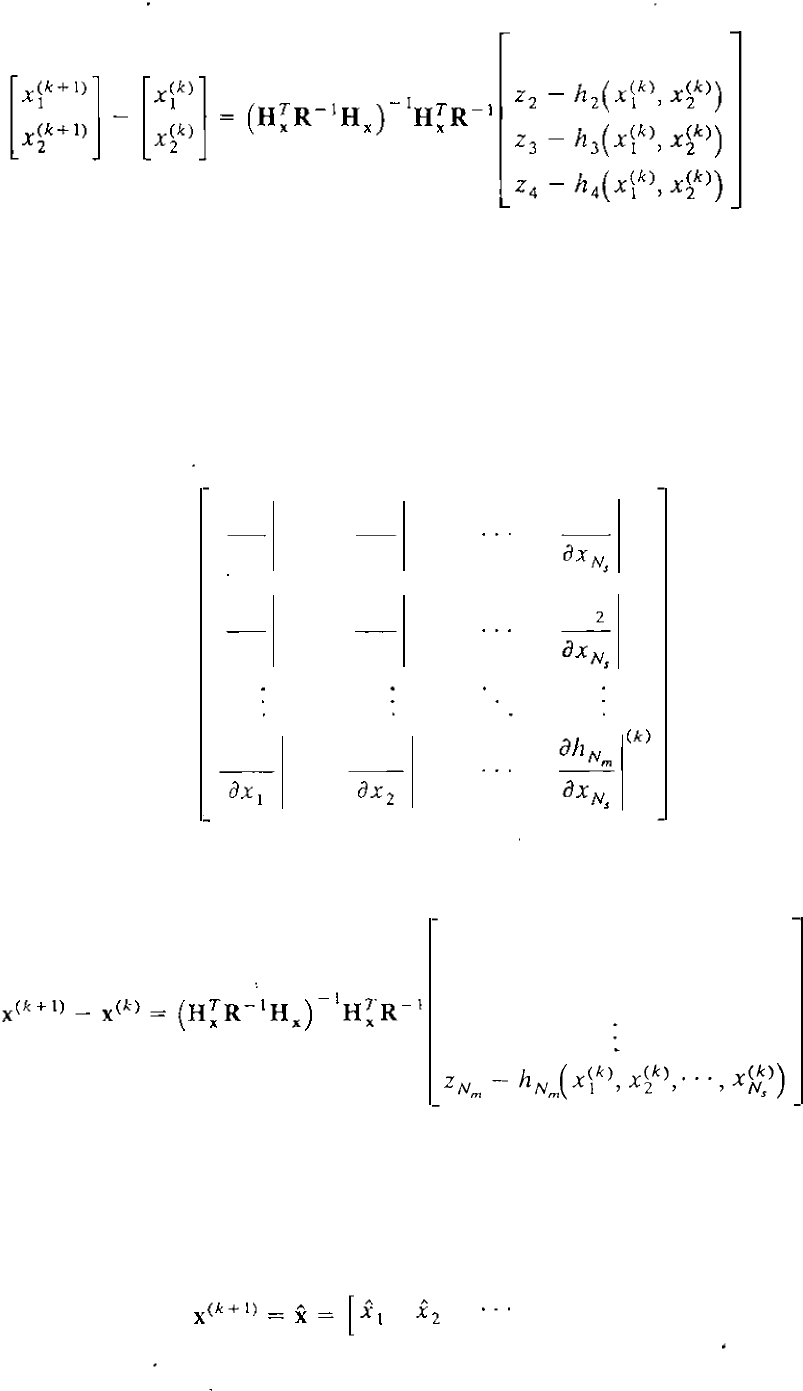
equation
15.4 POWER SYSTEM STATE ESTIMATION
667
Z -h (X(k) X(k»)
1 1
l' 2
(15.60)
For convenience the iteration counter k has been omitted from Hx in Eq.
05.60). However, at each iteration the elements of the jacobian Hx and the
quantities Z
j
-h
/
xik), X�k») are evaluated from the latest available values of
the state variables until two successive solutions have converged to within a
specied precision index E; that is, until Ix�k+
l
) - x�
k
)
1 <
E for every i.
When there are N, state variables and a larger number Nm of measure
ments, the rectangular form of H x fo r iteration k is given by
ah]
(
k
)
all,
(
k
)
ah
(k
)
1
a
x
, aX
2
3
h
z
(k
)
ah2
(k)
Bh (k)
2
H
=
x
aX
1
aX2
(15
.
61)
ah
N
(
k
)
In
h
(
k
)
a
N
m
and Eq. 05.60) assumes the general iterative form
z -h (X(
k) X(k) . .. x(k»)
1 1 l' 2' 'Ns
Z
-
h
(X(k) X(k) . .. X(k»)
2 2 l' 2' 'Ns
(15 .62)
At convergence the solution X(k + 1) corresponds to the weighted least-squares
estimates of the state variables, which we denote by
�
]
T
x
N•
(15 .63)

CR 15 STATE ESTIMATION OF POWER SYSTEMS
To check the estimates using the same statistical tests as before, wc
• Compute the corresponding measurement errors using
• Evaluate the sum of squares f according to Eq. (15.44), and
(
15
.64
)
• Apply the chi-square test of Sec. 15.3 to check for the presence of bad
measuremen ts.
To illustrate the procedures for linearizing and iteratively solving the ac power
system equations to obtain estimates of the states, let us consider Examples 15.5
and 15.6, which now follow.
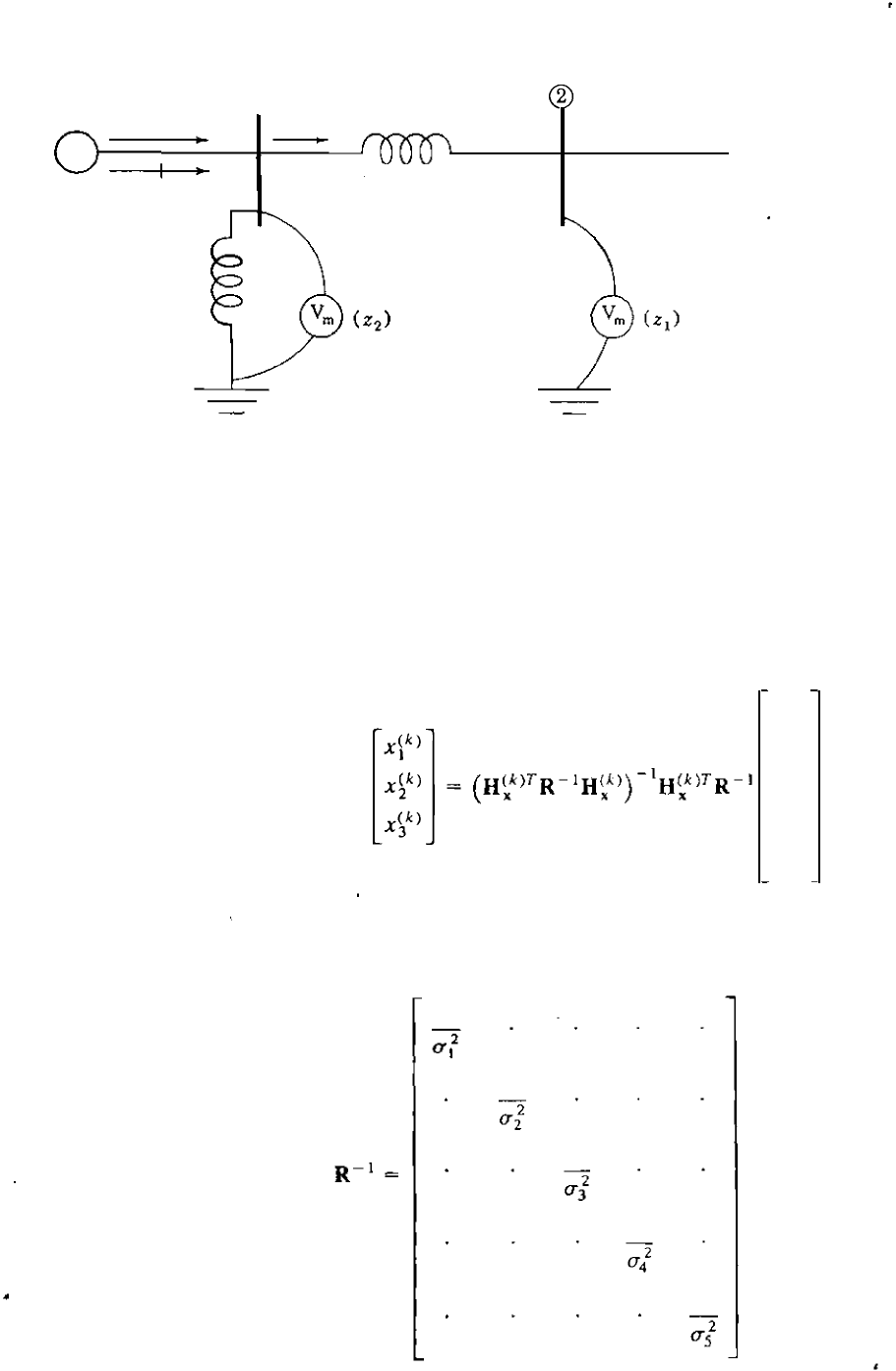
Example 15.5. Two voltmeters, two varmeters, and one wattmeter are installed on
the system of Fig. 9.3 to measure the following ve quantities:
bus voltage magnitude:
z
1
=
1V2!
bus voltage magnitude:
Z
2
=
I
V
I
I
bus reactive-power injection:
z
3
=
Q
1
line P-flow from bus to bus :
Z
4
=
Pl
2
line Q-flow from bus @ to bus :
Z
5
=
Q
2'
as shown in Fig. 15.4 on page 670. Formulate the linearized equations for
calculating the weighted least-squares estimates of the system states.
Solion . In this two-bus example we choose 0, = 0° as the reference angle and
the three unknown state variables as X
I
=
O2, X2
= I
V
2
1, and x3
=
IV
I
I. The rst
two state variables are the same as for the power-ow study of Example 9.3. The
third state variable x
3
=
I
V
I
I
is necessa here (unlike in the power-ow problems)
because the magnitude of the voltage at bus is uncertain and has to be
estimated.
Expressions for the line ows in terms of the state variables are given by
Eqs. (9.36) and (9.37) as follows:
For the reactive power Q
1
injected into the network at bus of Fig. 15.4,

15.4 POWER SYSTEM STATE ESTIMATION
669
Eq. (9.39) leads to
Note that
Q
r includes the reactive power in the reactance of j6.0 per unit from
bus
to neutral. The above equations allow us to write the following expressions
for the measurement errors in the k th iteration as
e(
k
)
=
z -
h
(X(
k
)
X(k) X(k))
=
z
-
X(k
)
I I I J , 2 ' 3 1 2
e(
k
)
=
z
-
h
(X(k) X(k)
X(k)) =
z -
X(k)
2
221 '2'
3
2
3
In the same iteration the partial derivatives of h), h2, and h
3
are evaluated
according to Eq. (15.61), which now becomes
H
(k)
=
x
a
h
1
(k)
a
h
1
(
k
)
a
x
)
a
X
2
a
h
2
(
k
)
a
h
2
(
k
)
aX
l
a
X
2
a
h
3
(
k
)
a
h
3
(
k
)
a
X
l
a
X
2
a
h4
(
k
)
ah4
(k)
ax)
a
X
2
h
s
(
k
)
a
h
s
(
k
)
ax)
a
X
2
0
.. 0
4X
(k)
X
(k)
sin
X(k)
3
21
- 4X
(k)
X
(k)
cos X
(
k)
3
2
I
4
X(k)X(k)
sin X
(k)
3
2
1
a
h
l
a
X
3
a
h
2
a
X
3
a
h
3
a
X3
a
h4
a
X
3
ah
a
X
3
(k)
(k)
(
k
)
(
k
)
(
k
)
1
0
- 4X
(
k)
cos
X
(k)
3
1
-
4
X
(k)
sin X
(
k)
3
I
8x
- 4X
(
k)
cos X
(
k)
2
3
I
0
1
X
(
k)
- 4
X(k)
cos
X(k)
3 3
2
1
-
4
X
(k)
sin
X
(k
)
2
1
-
4X
(k)
cos X
(k)
2
1
670
CHAER 15 STATE ESTIMATION OF POWER SYSTEMS
1V11&
I
V
2
1
&
2
P
I
P
1
2(Z4)
P
2
1
P
z
- - -
I -
Ql
(Z
3
)
Q12
)0.25
Q21
(Z
S)
Q2
j6.0
GURE 15.4
0
.3
t
I
J
0
6
The one-line diagram of Example 15.5 showing the quantities
1
V2 1, IV)I. Q). P12' and Q21
constituting the measurement set {Zl' z
2
' z
3
' Z4, z
s
}
·
Based on H�
k
)
and eJ
k
)
, the counterpart of Eq. 05.62) for calculating the state
estimates is of the form
[
X
�
k
+
J
)
1
X
(
k
+
1)
_
2
x
(
k
+
1)
3
with the weighting matrix of reciprocal variances given by
1
1
1
1
1
e
l
k
)
e
(
k
)
2
(
k
)
e
3
e
�
k
)
e
(
k
)
5

1
5
.4 POWER SYSTEM STATE TIMATION 671 .
The equations developed in the preceding example are important illustrations
of the general procedure and fo the basis of the numerical calculations in
Examples
1
5.6 and
1
5.7 for estimating the system state.
Example 15.6. Tclemetcrcd measurements on the physical system corresponding
to Fig. 15.4 show that the per-unit values of the ve measured quantities are
z\ =
I
V2 1 = 0.92
Z
5 = Q21 = 0.305
The variances of the measurement errors are specied in per unit as
2
2 ( )2
I
=
2
= 0.01 a} =
- 2008 — 2025 «СтудМед»
