Steve M., Darby D.M., Geostatistics Explained - An Introductory Guide for Earth Scientists
Подождите немного. Документ загружается.


These hypotheses are called the alternate and null hypotheses respec-
tively. Importantly, the null hypothesis is always stated as the hypothesis of
“no difference” or “no effect.” So, looking at the two hypotheses above, the
second “does not” hypothesis is the null hypothesis and the first is the
alternate hypothesis. This is a tedious but very important convention
(because it clearly states the hypothesis and its alternative) and there will
be several reminders in this book.
2.7 Conclusion
There are five components to an experiment – (1) formulating a hypothesis,
(2) making a prediction from the hypothesis, (3) doing an experiment or
sampling to test the prediction, (4) analyzing the data, and (5) deciding
whether to retain or reject the hypothesis.
The description of scientific method given here is extremely simple and
basic and there has been an enormous amount of philosophical debate
about how science is done (see Box 2.1). For example, more than one
hypothesis might explain a set of observations and it may be difficult to
test these by progressively considering each one against its null. For further
reading, Chalmers (1999) gives a very clearly explained discussion of the
process and philosophy of scientific discovery.
Box 2.1 Two other views about scientific method
Popper’s hypothetico-deductive philosophy of scientific method, where
hypotheses are sequentially tested and always at risk of being rejected, is
widely accepted. In reality, however, scientists may do things a little
differently.
Kuhn (1970) argues that scientific enquiry does not necessarily pro-
ceed with the steady testing and survival or rejection of hypotheses.
Instead, hypotheses with some generality and which have survived initial
testing become well-established theories or “paradigms” which are rela-
tively immune to rejection even if subsequent testing may find evidence
against them. A few negative results are used to refine the paradigm to
make it continue to fit all available evidence. It is only when the negative
2.7 Conclusion 13

2.8 Questions
(1) Describe the “hypothetico-deductive” model of how science is done,
including the null and alternate hypotheses, the concepts of disproof
and the importance of a negative outcome.
(2) Why is it important to collect data from more than one sampling unit or
experimental unit when testing a hypothesis?
evidence becomes overwhelming that the paradigm is rejected and
replaced by a new one.
Lakatos (1978) also argues that a strict hypothetico-deductive process
of scientific enquiry does not necessarily occur. Instead, fields of enquiry,
called “ research programmes” are based on a set of “core” theories that
are rarely questioned or tested. The core is surrounded by a protective
“belt” of theories and hypotheses that are tested. A successful research
program is one that accumulates more and more theories that have
survived testing within the belt, which provides increasing protection
for the core. If, however, many of the belt theories are rejected, doubt will
eventually be cast on the veracity of the core and of the research program
itself, which will be replaced by a more successful one.
These two views and the hypothetico-deductive view are not irrecon-
cilable. In all cases observations and experiments provide evidence either
for or against a hypothesis or theory. In the hypothetico-deductive view
science proceeds by the orderly testing and survival or rejection of
individual hypotheses, while the other two views reflect the complexity
of theories required to describe a research area and emphasize that it
would be foolish to reject a theory outright on the basis of limited
negative evidence.
14 “Doing science”: hypotheses, experiments and disproof

3 Collecting and displaying data
3.1 Introduction
One way of generating hypotheses is to collect data and look for patterns.
Often, however, it is difficult to see any pattern from a set of data, which may
just be a list of numbers. Graphs and descriptive statistics are very useful for
summarizing and displaying data in ways that may reveal patterns. This
chapter describes the different types of data you are likely to encounter and
discusses ways of displaying them.
3.2 Variables, sampling units and types of data
In earth science applications, we usually consider three different types of data:
(1) Data organized in a sequence along a continuum of distance or time.
These data can be thought of as occurring in one dimension. For example,
you might be analyzing the composition or mineralogy of a drill core and
need to interpret spatial variation up and down the section.
(2) Data where sampling is done relative to some geographic or other type
of spatial context. These are usually two-dimensional data. Geologic
maps, contour diagrams, trend surface analyses and studies of spatial
relationships in thin sections all present opportunities to relate data to a
2-D system.
(3) Multivariate data in which the 1- or 2-D locations of the sampled data
are not relevant. Most types of chemical data fall into this category.
The particular attributes you measure when you collect data are called
variables (e.g. a chemical analysis, observations of humidity and air temper-
ature, the thickness of some geological strata). These data are collected from
each sampling unit, which may be an individual (e.g. a single piece of rock)
15

or a defined item (e.g. a square meter of the outcrop, a specific stratigraphic
unit, or a particular locality).
If you only measure one variable per sampling unit the data set is uni-
variate. Data for two variables per unit are bivariate, while data for three or
more variables measured on the same sampling unit are multivariate.
Variables can be measured on four scales – ratio, interval, ordinal or
nominal.
A ratio scale describes a variable whose numerical values truly indicate
the quantity being measured.
*
There is a true zero point below which you cannot have any data
(for example, if you are measuring the length of feldspar crystals in a
thin section, you cannot have a crystal of negative length).
*
An increase of the same numerical amount indicates the same quantity
across the range of measurements (for example, a 0.2 mm and a 2 mm
feldspar will have grown by the same amount if they both increase in
length by 10 mm).
*
A particular ratio holds across the range of the variable (for example,
a 200 μm feldspar grain is twenty times longer than a 10 μm grain and a
100 μm grain is also twenty times longer than a 5 μm one).
An interval scale describes a variable that can be less than zero.
*
The zero point is arbitrary (for example, temperature measured in
degrees Celsius has a zero point at which water freezes), so negative
values are possible. The true zero point for temperature, where there is
a complete absence of heat, is zero kelvin (about –273 °C), so (unlike
Celsius) the kelvin is a ratio scale.
*
An increase of the same numerical amount indicates the same quantity
across the range of measurements (for example, a 2 °C increase indicates
the same increase in heat whatever the starting temperature).
*
Because the zero point is arbitrary, a particular ratio does not hold across
the range of the variable. For example, the ratio of 6 °C compared to 1 °C
is not the same as 60 °C to 10 °C. The two ratios in terms of the kelvin
scale are 279:274 K and 333:283 K.
An ordinal scale applies to data where values are ranked – which means
they are given a value that simply indicates their relative order. For
example, five mountains with elevations of 10 000 m, 4500 m, 4300 m,
16 Collecting and displaying data

4000 m and 3984 m have been measured on a ratio scale. If you rank these in
order, from highest to lowest, as 5, 4, 3, 2 and 1, the data have been reduced
to an ordinal scale, but this is not very informative and does not mean that
the highest mountain is five times the elevation of the lowest. For ordinal
data, an increase in the same numerical amount of ranks does not necessa-
rily hold across the range of the variable.
A nominal scale applies to data where the values are classi fied according
to an attribute. For example, the breakdown of rocks at the Earth’s surface
can be classified as either chemical or mechanical weathering, so a sample of
different sediments can be subdivided into the numbers within each of these
two categories. You might have a sample of ten, of which three fall in the
“chemical” category and the remaining seven in the “mechanical” one.
The first three types of data described above can include either contin-
uous or discrete data. Nominal scale data (since they are attributes) can
only be discrete.
Continuous data can have any value within a range. For example, any
value of temperature is possible within the range from 10 °C to 20 °C, such
as 15.3 °C or 17.82 °C.
Discrete data are very different from continuous data because they can
only have fixed numerical values within a range. For example, the number of
electrons in an atom increases from one fixed whole number to the next,
because you cannot have a fraction of an electron.
It is important that you know what type of data you are dealing with
because this will be one of the factors that determines your choice of
statistical test.
3.3 Displaying data
A list of data may reveal very little, but a pictorial summary is a way of
exploring the data that might help you notice a pattern, which can help
generate or test hypotheses.
3.3.1 Histograms
Here is a list of the number of visits made to their lecturer’soffice by a sample
of 60 students chosen at random from 320 students in the course
Introductory Geoscience. These data are univariate, ratio scaled and discrete.
3.3 Displaying data 17

1, 1, 6, 1, 12, 1, 2, 6, 2, 7, 2, 2, 5, 2, 1, 2, 1, 9, 1, 8, 1, 1, 2, 5, 1, 6, 1, 1, 1, 5, 1, 1,
1, 2, 2, 3, 2, 3, 3, 3, 3, 3, 4, 5, 6, 7, 8, 9, 4, 1, 1, 9, 10, 1, 4, 10, 11, 1, 2, 3
It is difficult to see any pattern from this list of numbers, but you could
summarize and display these data by drawing a histogram. To do this you
separately count the number (the frequency) of cases for students who
visited never, once, twice, three times, through to the maximum number of
visits and plot these as a series of rectangles on a graph with the X axis
showing the number of visits and the Y axis the number of students in each
of these cases. Figure 3.1 shows a histogram of these data.
This visual summary shows that the distribution is skewed to the right –
most students made few visits for help, but there is a long upper “tail ” who
have made five or more visits. Incidentally, looking at the graph you
may be a little suspicious because every student made at least one visit.
This was because each of them had to visit the lecturer’soffice to pick up
an assignment during the first three weeks of c lass to ensure they knew
where to go if they did ever need help, so these data are somewhat
misleading in terms of indicating the neediness of the group. You may
be tempted to draw a line joining the midpoints of the tops of each bar to
indicate the shape of the distribution, but this implies that the data on the
X axis are continuous, which is not the case because visits are discrete
whole numbers.
Number of visits
Number of students
1234567 8 9 10 11 12
0
20
15
10
5
Figure 3.1 The number of visits made to their lecturer’soffice by a sample of
60 students chosen at random from 320 students in the course Introductory
Geoscience.
18 Collecting and displaying data

3.3.2 Frequency polygons or line graphs
If the data are continuous, it is appropriate to draw a line linking the
midpoint of the tops of each bar in the histogram. Here is a geological
example for some continuous data that can be summarized as a histogram
or as a frequency polygon (often called a line graph). Carbon isotope data
are very useful for understanding the global distribution of carbon between
the Earth’s atmosphere, seawater and carbonate minerals. The δ
13
Cof
carbonate minerals can provide information about variations of δ
13
Cin
ocean water, which can be related to the global carbon cycle and palae-
oceanographic circulation patterns.
A sample of 28 “muddy” limestones (wackestones) was collected from an
extended outcrop, and isotopic analyses for δ
13
C ‰ were obtained. Nothing
is very obvious from this list of results:
1.01, 0.59, 2.32, 0.19, −2.39, −3.76, −0.8, 1.6, 0.28, −1.62, −0.33, −1.26,
−0.01, 1.36, 0.99, 1.12, −0.45, 0.71, 1.12, −0.72, 1.36, 1.59, 2.27, 2.25, 3.05,
2.58, 1.94, 3.28
Because the data are continuous, they are not as easy to summarize as the
discrete data in Figure 3.1. To display a histogram for continuous data you
need to subdivide the data into the frequency of cases within a series of
intervals of equal width. First you need to look at the range of the data (here
δ
13
C ‰ varies from a minimum of −3.76 through to a maximum of 3.28)
and decide on an interval width that will give you an informative display of
the data. Here the chosen width is 1.0 ‰. Therefore, starting from −4.0 ‰,
this will give 8 intervals, the first of which is −4to−3.01 ‰. The chosen
interval width needs to be one that shows the shape of the distribution: there
would be no point in choosing a width that included all the data in just two
intervals because you would only have two bars on the histogram. Nor
would there be any point in choosing more than 20 intervals because this
would give a lot of bars with each containing only a few data.
Once you have decided on an appropriate interval size, you need to count
the number of cases with δ
13
C values that fall within each interval
(Table 3.1) and plot these frequencies on the Y axis against the intervals
(indicated by the midpoint of each interval) on the X axis. This has been
done in Figure 3.2(a). Finally, the midpoints of the tops of each rectangle
have been joined by a line to give a frequency polygon, or line graph
(Figure 3.2(b)).
3.3 Displaying data 19

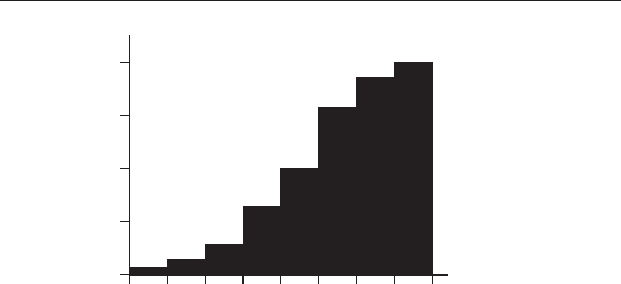
3.3.3 Cumulative graphs
Often it is useful to display data as a histogram of cumulative frequencies.
This is a graph that displays the progressive total (starting at zero, or zero
percent and finishing at the sample size or 100%) on the Y axis against the
increasing value of the variable on the X axis. Figure 3.3 gives an example,
using the data from Table 3.1.
A cumulative frequency graph can never decrease. Figure 3.3 displays the
data in Table 3.1 as a cumulative frequency histogram.
Table 3.1 Summary of δ
13
C ‰ data for limestones listed as frequencies
and cumulative frequencies.
Cumulative Frequency
Interval range
δ
13
C ‰ Cases Total Percent
−4to−3.01 1 1 3.6
−3to−2.01 1 2 7.1
−2to−1.01 2 4 14.3
−1to−0.01 5 9 32.1
0 to 0.99 5 14 50.0
1 to 1.99 8 22 78.6
2 to 2.99 4 26 92.9
3 to 3.99 2 28 100.0
δ
13
C ‰
Frequency
(a)
–4
8
4
0
–3 –2 –1 0 1 2 3 4
δ
13
C‰
(b)
1
8
6
4
2
0
0–1–2–3–4 324
Figure 3.2 Carbon isotope data for 21 sampling units of limestone from the
same outcrop, displayed as (a) a histogram and (b) a frequency polygon or line
graph. The points on the frequency polygon (b) correspond to the midpoints
of the bars on (a).
20 Collecting and displaying data
Although we have given the rather tedious manual procedures for con-
structing histograms, you will find that most statistical software packages
(and spreadsheets) have excellent graphics programs for displaying your
data. These will automatically select an interval width, summarize the data
and plot the graph of your choice.
3.4 Displaying ordinal or nominal scale data
When you display data for ordinal or nominal scale variables, you need to
modify the form of the graph slightly because the categories are unlikely to
be continuous, so the bars need to be separated to clearly indicate the lack of
continuity. Here is an example for some nominal scale data. Table 3.2 gives
the locations of 594 tornadoes during the period from 1998–2007 in the
southeastern states of the US.
These can be displayed on a bar graph with the categories in any order along
the X axis and the number of cases on the Y axis (Figure 3.4(a)). It often helps
to rank the data in order of magnitude to aid interpretation (Figure 3.4(b)).
3.5 Bivariate data
Data where two variables have been measured on each sampling unit can
often reveal patterns that may suggest hypotheses, or be useful for testing
them. Here is another case where the mineral apatite affects public health (in
Count
δ
13
C‰
–4 –3 –2 –1 0 1 2 3 4
28
21
14
7
0
Figure 3.3 A cumulative frequency histogram for δ
13
C data for limestones.
3.5 Bivariate data 21

Chapter 2 there was an example where apatite was used to clean up lead
waste – this is about hydroxylapatite in your teeth). Table 3.3 gives two lists
of bivariate data for the number of dental caries (these are the holes that
develop in decaying teeth) and age for 20 children between the ages of one
and nine years from each of the cities of Hale and Yarvard.
Looking at these data, there is not anything that stands out, apart from an
increase in the number of caries with age. If you calculate descriptive
statistics such as the average age and average number of dental caries for
each of the two groups (Table 3.4) they are not very informative either. (You
probably know how to calculate the average for a set of data and this
procedure will be described in Chapter 7, but the average is the sum of all
the values divided by the sample size.)
Table 3.4 shows that the sample from Yarvard had slightly more caries on
average than the one from Hale, but this is not surprising because the
Yarvard sample was an average of one year older. If, however, you graph
these data, patterns emerge. One way of displaying bivariate data is a two-
dimensional plot with increasing values of one variable on the horizontal
(or X axis) and increasing values of the second variable on the vertical
(or Y axis). Figure 3.5 shows both sets of data with the number of caries
(Y axis) plotted against child age (X axis) for each city.
Table 3.2 Preliminary data on tornado occurrence in
southeastern US states from 1998–2007, according to the
NOAA National Weather Service Storm Prediction Center
(www.spc.noaa.gov/wcm/).
Location
Number of tornadoes
1998–2007
Texas 95
Oklahoma 68
Louisiana 38
Arkansas 68
Mississippi 68
Alabama 64
Georgia 48
Tennessee 44
North Carolina 36
South Carolina 48
Florida 17
22 Collecting and displaying data
