Spohn H. Dynamics of Charged Particles and their Radiation Field

Подождите немного. Документ загружается.

Notes and references 63

Such reasoning yields no rate of convergence. The situation improves in the case

where q

∗

is a stable local minimum of φ

.Welinearize the Maxwell equations at

∗

= S

∗

. The solution to the linearized equations converges exponentially fast

to zero. Therefore, once q(t) is in the vicinity of q

∗

, the velocity decays exponen-

tially ensuring (5.34). In particular, if φ

is strictly convex and if (W ) holds, then

the asymptotics (5.35) of Theorem 5.3 hold for every Y (0) ∈

A standard situation not covered by (i) and (ii) is the motion in a uniform mag-

netic ﬁeld. Even if one assumes that the motion is bounded, one can only conclude

that v(t) → 0. The attractor

A equals R

.Physically one would expect the charge

to spiral inwards and to come to rest at its center of gyration. Another instruc-

tive example is the motion in a conﬁning φ

with a ﬂat bottom, say {x ||x|≤1}

and A

= 0. Each time the particle is reﬂected by the conﬁning potential, it loses

energy. Thus v(t) → 0ast →∞,butq(t) has no limit.

Notes and references

Section 5.1

The long-time asymptotics are studied in Komech and Spohn (2000), where the

details of the proof can be found. See also Komech, Spohn and Kunze (1997).

Pitt’s version of the Wiener theorem is proved in Rudin (1977), Theorem 9.7(b).

We remark that Theorem 5.1 provides no rate of convergence. Thus to investigate

the asymptotics of the velocity and position requires extra considerations.

Theorem 5.1 can also be read that under the Wiener condition the Abraham

model admits no periodic solution. In the literature, Bohm and Weinstein (1948),

Eliezer (1950), and in particular the review by Pearle (1982), periodic solutions of

the Abraham model have been reported repeatedly for the case of a charged sphere,

i.e. ϕ(x) = (4π a

)

−1

δ(|x|−a), which is not covered by Theorem 5.1 since (W )

is violated. These computations invoke certain approximations and it is not clear

whether the full model, as deﬁned by (2.39)–(2.41), has periodic solutions. Pearle

(1977) argues that in the Nodvik model there are no periodic solutions. Kunze

(1998) proves that if there is a periodic solution, its frequency is determined by the

zeros of the radial part of the form factor ϕ, which under (C) form a discrete set.

If ϕ has a zero, then the linearized system admits a periodic solution. However, the

full nonlinear equations have no periodic solution, at least in a small neighborhood

of the linearized periodic solution.

As will be explained in chapter 11, the Abraham model extends in the obvious

waytothe dynamics of many charges. The argument of Theorem 5.1 applied to

this case yields that the acceleration of the center of mass relaxes to zero. One

64 Long-time asymptotics

would expect particles to form neutral lumps, each of which is traveling at constant

velocity for large t.Noargument towards a proof is in sight.

Section 5.2

The contraction method was ﬁrst developed in Komech, Kunze and Spohn (1999).

Komech and Spohn (1998) prove the convergence to the soliton manifold in the

case of a scalar wave ﬁeld requiring only (W ) and not the restriction |e| < ¯e.No

convergence rates are obtained. Their result is extended to the Abraham model by

Imaikin, Komech and Mauser (2003). Orbital stability was established before by

Bambusi and Galgani (1993). Bambusi (1994) investigates the long-time stability

in the case of an attractive central potential.

Section 5.3

Our results are based on Imaikin, Komech and Spohn (2002). The linearization

argument is fully carried out in Komech, Spohn and Kunze (1997).

Adiabatic limit

If we assume that the mass of an electron is purely electromagnetic, then by equat-

ing its rest energy and electrostatic Coulomb energy the charge distribution must

be concentrated in a ball of radius

= 3 × 10

−13

cm (6.1)

which is the so-called classical electron radius. Quantum mechanically one argues

that on the basis of light scattering the electron appears to have an effective size

of the order of the Compton wavelength λ

= m

/c = (e

/c)

−1

= 137 r

Thus empirically R

is limited to r

≤ R

≤ 137r

. Electromagnetic ﬁelds which

can be manipulated in the laboratory vary little over that length scale. r

deﬁnes

a time scale through the time span for light to travel across the diameter of the

charge distribution,

= r

/c = 10

−23

s , equivalently a frequency ω

= 10

Hz . (6.2)

Again, manufactured frequencies are much smaller than ω

. Space-time variations

as fast as (6.1) and (6.2) lead us deeply into the quantum regime. Thus it is natural

and physically compelling to study the dynamics of a charged particle under exter-

nal potentials which vary slowly on the scale of the charge radius R

, which is the

only length scale available. This means we have to introduce a scale of potentials

and enquire about an approximately autonomous particle dynamics with an error

depending on the scale under consideration. We will introduce such a scheme in the

following section. The resulting problem has many similarities with the derivation

of hydrodynamics from Newtonian particle dynamics – with the most welcome

bonus that it is simpler mathematically by many orders of magnitude. Still, the

comparison is instructive.

66 Adiabatic limit

6.1 Scaling limit for external potentials of slow variation

For the Abraham model, see Eq. (2.41), the Lorentz force has in addition to the

dynamical ﬁelds E(x, t), B(x, t) also prescribed external ﬁelds, which are the gra-

dients of the external potentials φ

(x), A

(x).

We want to impose the condition that φ

and A

are slowly varying on the scale

of R

.Formally we introduce a small dimensionless parameter ε and consider the

potentials

(εx), A

(εx), (6.3)

which are slowly varying in the limit ε → 0. Most of our results extend to po-

tentials which vary also slowly in time. For simplicity we restrict ourselves to

time-independent potentials here. Clearly, ε appears as a parameter of the poten-

tial, just like ω

is a parameter of the harmonic oscillator potential

mω

. But

ε should really be thought of as a bookkeeping device which orders the magnitude

of the various terms and the space-time scales according to the powers of ε. Such

a scheme is familiar from very diverse contexts and appears whenever one has to

deal with a problem involving scale separation.

So how small is ε? From the discussion above one might infer that if φ

, A

vary over a scale of 1 mm, then ε = 10

−12

. This is a totally meaningless statement,

because eφ

, e A

have the dimension of energy and thus the variation depends

on the adopted energy scale. In (6.3) we merely stretch the spatial axes by a factor

−1

and ﬁx the energy scale. Since from experience this point is likely to be con-

fusing, let us consider the speciﬁc example of a charge revolving in the uniform

magnetic ﬁeld B

= (0, 0, B

). The corresponding vector potential is linear in x,

and to introduce ε as in (6.3) just means that the magnetic ﬁeld strength equals

εB

. The limit ε → 0isalimit of small magnetic ﬁeld strength relative to some

reference ﬁeld B

. Thus to obtain ε we ﬁrst have to determine the reference ﬁeld

and compare it with the magnetic ﬁeld of interest. This shows that in order to ﬁx ε

we have to specify the physical situation in detail, in particular the external poten-

tials, the mass of the particle, the charge of the particle, γ(v), and the time span of

interest.

The scaling scheme (6.3) has the great advantage that the analysis can be car-

ried out in generality. In a second step one has to ﬁgure out ε for a concrete sit-

uation, which leads to a quantitative estimate of the error terms. For instance, if

in the case above we consider an electron with velocities such that γ ≤ 10, then,

by comparing the Hamiltonian term and the friction term, the reference ﬁeld turns

out to be B

= 10

gauss. Laboratory magnetic ﬁelds are less than 10

gauss and

thus ε<10

−12

.Inthis and many other concrete examples, ε is very small, less

than 10

−10

, which implies that, ﬁrstly, all corrections beyond radiation reaction

6.1 Scaling limit for external potentials of slow variation 67

are negligible. Secondly, we do not have to go each time through the scheme in-

dicated above and may as well set ε = 1 thereby returning to conventional units.

Still on a theoretical level the use of the scale parameter ε is very convenient. In

an appendix to this section we will work out the example of a constant magnetic

ﬁeld more explicitly. If the reader feels uneasy about the scaling limit, (s)he should

consult this example ﬁrst.

Adopting (6.3), Newton’s equations of motion now read



γ v(t)



= e



(q(t), t ) + ε E

(εq(t))

+v(t) ×



(q(t), t ) + ε B

(εq(t))



, (6.4)

where

=−∇φ

, B

=∇×A

. (6.5)

Note that if E

, B

are smeared by ϕ,aswould be proper, the resulting error in

(6.4) is of order ε

, which can be ignored for our purposes.

Equation (6.4) has to be supplemented with Maxwell’s equations (2.39), (2.40).

Our goal is to understand the structure of the solution for small ε, and as a ﬁrst

qualitative step one should discuss the rough order of magnitudes in powers of ε.

But before that we have to specify the initial data. We give ourselves q

, v

the initial position and velocity of the charge. The initial ﬁelds are assumed to be

Coulombic, i.e. of the form of a charge soliton centered at q

with velocity v

compare with (4.28), which we formalize as

Condition (I ):

Y (0) = S

. (6.6)

Equivalently, according to (4.31), (4.32), we may say that the particle has traveled

freely with velocity v

for the inﬁnite time span (−∞, 0]. At time t = 0 the ex-

ternal potentials are turned on. Geometrically, our initial data are exactly on the

soliton manifold

S considered as a submanifold of the phase space M.Ifthere

are no external forces, the solution stays on

S and moves along a straight line. For

slowly varying external potentials as in (6.3) we will show that the solution stays

ε-close to

S in the local energy distance.

On general grounds one may wonder whether such speciﬁc initial data are re-

ally required. In analogy to hydrodynamics, we call this the initial slip problem. In

times of order t

(= R

/c),the ﬁelds close to the charge acquire their Coulombic

form while the external forces are still negligible; compare with ﬁgure 6.1. How-

ever, during that period the particle might gain or lose in momentum and energy

through the interaction with its own ﬁeld and the data at time t

close to the particle

68 Adiabatic limit

y(t)

Figure 6.1: Schematic phase space with attractive soliton manifold S.Away

from S the motion is fast, on S it is slow.

are approximately of the form S

˜q, ˜v

,where ˜q and ˜v are to be computed from the

full solution. Of course, at a distance ct away from the charge, the ﬁeld still re-

members its t = 0 data. Thus we see that the initial slip problem translates into the

long-time asymptotics of a charge at zero external potentials but with general ini-

tial ﬁeld data. We refer to section 5.2, where this point has been studied in detail.

At the moment we just circumvent the initial slip by ﬁat.

Let us discuss the three relevant time scales, where we recall that t

= R

/c.

(i) Microscopic scale, t =

O(t

), q = O(R

).Onthis scale the particle moves

along an essentially straight line. The electromagnetic ﬁelds adjust themselves to

their comoving Coulombic form. As we will see, they do this with a precision

O(ε)

in the energy norm.

(ii) Macroscopic potential scale, t =

O(ε

−1

), q = O(ε

−1

). This scale

is deﬁned by the variation of the potentials, i.e. on this scale the potentials are

(x), A

(x). The particle follows the external forces. Since it is in company

with almost Coulombic ﬁelds, the particle responds to the forces according to the

effective energy–momentum relation, which we determined in chapter 4. On the

macroscopic scale the motion is Hamiltonian up to errors of order ε. There is no

dissipation of energy and momentum.

(iii) Macroscopic friction scale. Accelerated charges lose energy through

radiation, which means that there must be friction corrections to the effective

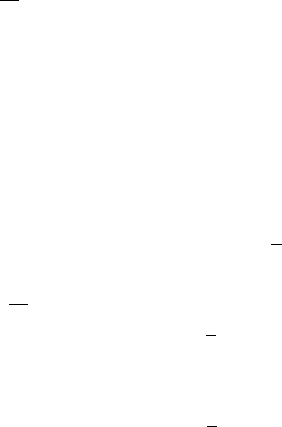
6.1 Scaling limit for external potentials of slow variation 69

Hamiltonian motion. According to Larmor’s formula the radiation losses are pro-

portional to ˙v(t)

.Since the external forces are of the order ε, these losses are

proportional to ε

when measured in microscopic units. Integrated over a time

span ε

−1

the friction results in an effect of order ε. Thus we expect order ε

dissipative corrections to the conservative motion on the macroscopic scale.

Followed over the even longer time scale ε

−2

, the radiation reaction results in

O(1) deviations from the Hamiltonian trajectory.

On the friction time scale the motion either comes to a standstill or stays uni-

form. In addition, as will be shown, the dissipative effective equation has the same

long-time behavior as the true solution. Thus we expect no further qualitatively

distinct time scale beyond the friction scale.

From our description, in a certain sense, the most natural scale is the macro-

scopic scale and we transform Maxwell’s and Newton’s equations to this new scale

by setting



= εt , x



= εx . (6.7)

We have the freedom of how to scale the amplitudes of the dynamic part of the

electromagnetic ﬁelds. We require that their energy is independent of ε. Then



, t



) = ε

−3/2

E(x, t), B



, t



) = ε

−3/2

B(x, t ). (6.8)

Finally the new position and velocity are



) = εq(t), v



) = v(t), (6.9)

so that



= v



. There is little risk of confusion in omitting the prime. We then

denote

(t) = εq(ε

−1

t), v

(t) = v(ε

−1

t), ϕ

(x) = ε

−3

ϕ(ε

−1

x), (6.10)

which means that



x ϕ

(x) = 1 independent of ε and that ϕ

is supported in

a ball of radius εR

.Inthe macroscopic coordinates the coupled Maxwell’s and

Newton’s equations read

∂

B(x, t ) =−∇×E(x, t ),

∂

E(x, t) =∇×B(x, t) −

√

εeϕ

(x − q

(t))v

(t),



γ v

(t)



= e



(t)) + v

(t) × B

(t))



√

ε e



(t), t) + v

(t) × B

(t), t)



(6.11)

together with the constraints

∇·E =

√

ε eϕ

(·−q

(t)) , ∇·B = 0 . (6.12)

70 Adiabatic limit

On the macroscopic scale the conserved energy is

mac

= m

γ(v) + eφ

(q) +





E(x)

+ B(x)



. (6.13)

Also the initial data have to be transformed and become

Condition (I

(0) = S

= (E

(x − q

), B

(x − q

), q

, v

) (6.14)

with

=−∇φ

+ v(v ·∇φ

), B

=−v ×∇φ

, (6.15)

where now



(k) =

√

ε eϕ(εk)

− (v · k)

. (6.16)

On the macroscopic scale, the scaling parameter ε can be absorbed into the

“effective” charge distribution

√

εeϕ

. Its electrostatic energy,



k ε|ϕ

(k)|



k|ϕ(k)|

, (6.17)

is independent of ε, while its charge



√

εϕ

(x) =

√

ε e (6.18)

vanishes as

√

ε. Recall that ε is a “bookkeeping device”.

We argued that on the macroscopic scale the response to external potentials in

the motion of the charges is of order one. We thus expect that q

(t) tends to a

nondegenerate limit as ε → 0, i.e.

lim

ε→0

(t) = r(t), lim

ε→0

(t) = u(t). (6.19)

The position r(t) and velocity u(t) should be governed by an effective Lagrangian.

In section 4.1 we determined the effective inertial term. If the potentials add in as

usual, one has

eff

(q, ˙q) = T ( ˙q) − e



(q) −˙q · A

(q)



, (6.20)

which results in the equations of motion

˙r = u , m(u) ˙u = e(E

(r) + u × B

(r)) . (6.21)

6.1 Scaling limit for external potentials of slow variation 71

The velocity-dependent mass m(u) has a bare and a ﬁeld contribution. From (4.12)

we conclude that

m(u) =

(u)

(6.22)

as a 3 × 3 matrix. If instead of the velocity we introduce the canonical momentum,

p, then the effective Hamiltonian reads

eff

(r, p) = E

eff

( p − e A

(r)) + eφ

(r) (6.23)

with Hamilton’s equations of motion

˙r =∇

eff

, ˙p =−∇

eff

. (6.24)

Our plan is to establish the limit (6.19) and to investigate the corrections due to

radiation losses.

6.1.1 Appendix 1: How small is ε?

We consider an electron moving in an external magnetic ﬁeld oriented along

the z-axis, B

= (0, 0, B

). The corresponding vector potential is A

(x) =

(−x

, x

, 0). According to our convention the slowly varying vector potential

is given by A

(εx) =

εB

(−x

, x

, 0). Thus B

is a reference ﬁeld strength,

which is to be determined, and B = ε B

is the physical ﬁeld strength in the lab-

oratory. The motion of the electron is assumed to be in the 1–2 plane and we set

v = (u, 0).According to section 9.2, example (iii), within a good approximation

the motion of the electron is governed by

γ ˙u = ω

⊥

− βω

u). (6.25)

Here u

⊥

= (−u

, u

), ω

= eB/m

c is the cyclotron frequency, and β =

/6πc

.The ﬁrst term is the Lorentz force and the second term accounts for

the radiation reaction.

We now choose the reference ﬁeld B

such that the two terms balance, i.e.

= (βe/m

−1

. (6.26)

For electrons

= 1.1 × 10

gauss (6.27)

and even larger by a factor (1836)

for protons. For a laboratory ﬁeld of 10

gauss

this yields

ε = 10

−12

. (6.28)

72 Adiabatic limit

Written in units of B

, (6.25) becomes

γ ˙u = εω

⊥

− εu) (6.29)

with βω

= 1, i.e.ω

= eB

c = 1.6 ×10

−1

. Thus friction is of relative

order ε and higher-order corrections would be of relative order ε

.Aswill be

demonstrated, the dimensionless scaling parameter ε serves as a bookkeeping de-

vice to track the relative order of the various terms contributing to the dynamics.

6.1.2 Appendix 2: Adiabatic protection

The adiabatic limit, as discussed above, relies on the fact that photons have zero

mass. If they had ﬁnite mass, radiation damping would be hindered. This point can

be most easily argued in the context of a scalar wave ﬁeld. Moreover, rather than

having a particle interacting with the ﬁeld, it sufﬁces to have a source ﬁxed at the

origin.

The scalar wave ﬁeld is denoted by φ with canonically conjugate momentum

ﬁeld π. They are governed by

∂

φ(x, t) = π(x, t), ∂

π(x, t) = φ(x, t) − κ

φ(x, t) + α(t)δ(x). (6.30)

α(t) is a smooth function vanishing outside the interval [0, T ]. Assuming that φ =

0, π = 0 initially we want to determine how much energy is radiated in the long-

time limit.

The local ﬁeld energy is given by

e(x, t) =



π(x, t)

+ (∇φ(x, t))

+ κ

φ(x, t)



(6.31)

from which, using (6.30), the energy current

=−π∇φ (6.32)

follows. The energy ﬂow through a sphere of radius R is given by

−



∞

dtR



ωπ(ω R, t)ω ·∇φ(ω R, t)

=−4π R



∞

dtπ(R, t)φ



(R, t)

=−4π



∞

dtRπ(R, R + t)Rφ



(R, R + t). (6.33)

The ﬁrst step uses radial symmetry of the solution to (6.30), while retaining the

notation for the radial ﬁelds and setting φ



(R, t) = ∂

φ(R, t), and the second step

uses the condition that the solution is supported inside the light cone. To separate