Spohn H. Dynamics of Charged Particles and their Radiation Field
Подождите немного. Документ загружается.

17.4 Fluorescence 263
z
1
(λ)
z
2
(λ)
z
31
(λ)
z
32
(λ)
ε
2
ε
1
ε
3
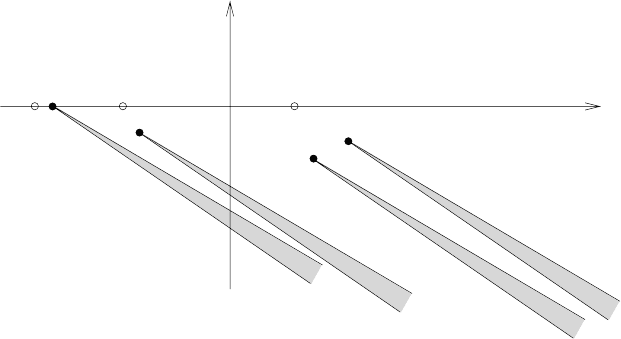
Figure 17.3: Spectrum of the rotated Hamiltonian H
λ
(iϑ) at small nonzero cou-
pling. The domain of analyticity is {z|Imz > −b
0
} with small b
0
> 0 and away
from the shaded regions.
as an m
j
× m
j
matrix for j = 1,... ,
¯
N . The eigenvalues of this matrix are:
Imz
jm
(λ), m = 1,... ,m
j
,toorder λ
2
.Tosecond-order the imaginary part of
the resonance poles agrees with the decay rates from the quantum master equa-
tion (17.32). Their real part coincides with the eigenvalues of H
at
corrected by the
Hamiltonian part of K
from (17.37). To obtain the full generator K
one has to
study the resonances of the Liouvillean as will be discussed in chapter 18.
17.4 Fluorescence
We have described in considerable detail how the atom decays to its ground
state, at least for small coupling. So what then are the spectral characteristics
of the fluorescent light? How does the theory account for the experimental fact
that the line shapes differ for equally and for unequally spaced unperturbed
energy levels? We will address such questions only within the weak coupling
theory.
The initial state of the atom is chosen to be a pure state ψ ∈
C
N
and that of the
field to be the vacuum. We want to determine e
−iH
λ
t
ψ ⊗ for small λ and large
t, order of λ
−2
. One method is to use second-order perturbation theory for the res-
onance poles of the resolvent, as explained for a particular case in the previous
section. Another method is to expand the resolvent ϕ ⊗
n
j=1
a
∗
(k
j
,λ
j
), (z −
H
λ
)
−1
ψ ⊗ and to resum all nonoverlapping internal photon lines lying in
between either the external photon legs or the atom legs. The results turn out to
be identical and have a simple physical interpretation.

264 Radiation
To state the approximation to e
−iH
λ
t
ψ ⊗,werewrite the generator of the
reduced atom dynamics as, compare with (17.37), (17.32),
L
D
ρ = [H
at
,ρ] + iλ
2
K
ρ
= [H
at
+ λ
2
H
− iλ
2
H
,ρ] + i
3
α=1
ω∈σ(
L
at
)
(ω)Q
α
(ω)
∗
ρ Q
α
(ω)
= L
D0
ρ + L
D1
ρ. (17.68)
Then
H
=
3
α=1
ω∈σ(L
at
)
(ω)Q
α
(ω)Q
α
(ω)
∗
=
3
α=1
¯
N
i, j=1
(ε
i
− ε
j
)P
j
Q
α
P
i
Q
α
P
j
,
(17.69)
and
H
=
3
α=1
ω∈σ(L
at
)
(ω)Q
α
(ω)Q
α
(ω)
∗
=
3
α=1
¯
N
i< j=1
(ε
i
− ε
j
)P
j
Q
α
P
i
Q
α
P
j
,
(17.70)
where we used the relation (ω) = 0 for ω ≥ 0. We introduce the convenient
shorthand
H
d
= H
at
+ λ
2
H
− iλ
2
H
. (17.71)
Note that H
d
is not symmetric. As a photon is emitted, the energy of the atom
decreases by at least one level, which is described by the atom lowering part of the
interaction Hamiltonian,
Q
−
· E
+
ϕ
=−i
¯
N
i< j=1
P
i
QP
j
⊗
λ=1,2
d
3
kϕ(k)
ω/2 ·e
λ
(k)a
∗
(k,λ)
.
(17.72)
With this notation the approximate solution is
e
−iH
λ
t
ψ ⊗
∼
=
e
−iH
d
t
ψ ⊗ +
¯
N −1
n=1
(−i)
n
0≤t
1
≤...≤t
n
≤t
dt
n
...dt
1
×e
−i(H
d
+H
f
)(t−t
n
)
λQ
−
· E
+
ϕ
... e
−i(H
d
+H
f
)(t
2
−t
1
)
×λQ
−
· E
+
ϕ
e
−i(H
d
+H
f
)t
1
ψ ⊗. (17.73)
The sum is finite, since (Q
−
)
¯
N
ψ = 0.
17.4 Fluorescence 265
Taking in (17.73) the trace over the atom results in the reduced state of the
photon field. Taking the trace over the field yields the reduced state of the atom.
But this state was already determined in section 17.2. To be consistent with it we
must have
tr
F
[|e
−iH
λ
t
ψ ⊗e
−iH
λ
t
ψ ⊗|] = e
−i
L
t
P
ψ
, (17.74)
at least for small λ, P
ψ
the projection onto ψ.If(17.74) holds, the case of an
arbitrary initial density matrix follows by linearity.
To prove (17.74) we insert (17.73) and obtain
tr
F
[|e
−iH
λ
t
ψ ⊗e
−iH
λ
t
ψ ⊗|] (17.75)
= e
−iH
d
t
P
ψ
e
iH
∗
d
t
+
¯
N −1
n=1
λ
2n
0≤t
1
≤...≤t
n
≤t
dt
n
...dt
1
×
0≤s
1
≤...≤s
n
≤t
ds
n
...ds
1
3
α
1
,β
1
=1
...
3
α
n
,β
n
=1
×
n
j=1
δ
α
j
β
j
h(s
j
− t
j
)e
−iH
d
(t−t
n
)
Q
−
α
n
e
−iH
d
(t
n
−t
n−1
)
Q
−
α
n−1
...Q
−
α
1
e
−iH
d
t
1
P
ψ
×e
iH
∗
d
s
1
Q
−∗
β
1
...Q
−∗
β
n−1
e
iH
∗
d
(s
n
−s
n−1
)
Q
−∗
β
n
e
iH
∗
d
(t−s
n
)
.
Since [H
at
, H
] = 0 = [H
at
, H
], one can use the spectral representation
e
−iH
d
t
=
¯
N
j=1
e
−iε
j
t
P
j
e
−iλ
2
H
t−λ
2
H
t
(17.76)
and insert it for each propagator in (17.75). On the time scale λ
−2
τ , τ = O(1), h(t)
decays quickly and the factors e
−iεt
are rapidly oscillating. The generic integral in
(17.75) is of the form
τ
0
dt
τ
0
dsλ
−2
h(λ
−2
(s − t))e
i(ε
i
−ε
j
)t/λ
2
e
−i(ε
m
−ε
n
)s/λ
2
. (17.77)
In the limit λ → 0itconverges to
min(τ, τ
)
dth(t)e
−i(ε
m
−ε
n
)t
δ
ε
i
−ε
j
,ε
m
−ε
n
= min(τ, τ
)(ε
m
− ε
n
)δ
ε
i
−ε
j
,ε
m
−ε
n
.
(17.78)

266 Radiation
Using (17.78) and (17.76), the small-λ limit of the expression in (17.75) is given
by
e
−iL
D0
t
P
ψ
+
¯
N −1
n=1
(−i)
n
0≤t
1
≤...≤t
n
≤t
dt
n
...dt
1
× e
−iL
D0
(t−t
n
)
L
D1
e
−iL
D0
(t
n
−t
n−1
)
...L
D1
e
−iL
D0
t
1
P
ψ
= e
−iL
D
t
P
ψ
(17.79)
as was to be shown.
The approximate solution (17.73) describes the decay of the atom and the build-
up of photons. Such details are experimentally inaccessible. However, what can
be easily seen are the spectral characteristics of the fluorescent light, which are
obtained from (17.73) in the limit t →∞(on the time scale λ
−2
). Then the atom
is in its ground state and
e
−iH
λ
t
ψ ⊗
∼
=
e
−i(ε
1
+λ
2
1
)t
ψ
1
⊗ e
−iH
f
t
φ, (17.80)
where φ is a photon state propagating freely to infinity through e
−iH
f
t
. φ can be
read off from (17.73) as
ψ
1
⊗ φ = P
1
ψ ⊗ +
¯
N −1
n=1
(−i)
n
0≤t
1
≤...≤t
n
<∞
dt
n
...dt
1
P
1
e
i(H
d
+H
f
)t
n
×λQ
−
· E
+
ϕ
...e
−i(H
d
+H
f
)(t
2
−t
1
)
λQ
−
· E
+
ϕ
e
−i(H
d
+H
f
)t
1
ψ ⊗.
(17.81)
The projection P
1
comes in, since states in (17.73) which are orthogonal to the
uncoupled ground state ψ
1
decay exponentially and only the piece parallel to ψ
1
persists in the long-time limit.
To see how (17.80) translates to the spectrum of the emitted light, it might be
useful to work out two concrete cases.
(i) Two-level atom.Weconsider two nondegenerate levels |1, |2 with resonance
poles z
j
= ε
j
+
j
− i
j
/2, j = 1, 2,
1
= 0. Initially the atom is in state |2.
Then the scattering state φ of (17.80) has only one photon, φ = (0,φ
1
, 0,...),
with wave function
φ
1
(k
1
,λ
1
) =
(
2
/2) + i(ε
2
+
2
− ε
1
−
1
− ω(k
1
))
−1
f
12
(k
1
,λ
1
), (17.82)
where
f
12
(k,λ) = eϕ(k)1|x|2·e
λ
(k)
ω(k)/2. (17.83)
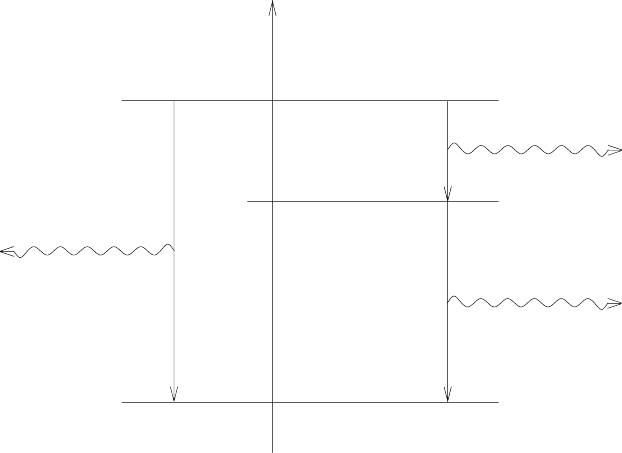
17.4 Fluorescence 267
E
ε
1
+ ∆
1
k
1,
λ
1
k
3,
λ
3
k
2,
λ
2
|1
|2
|3
ε
2
+ ∆
2
ε
3
+ ∆
3
Figure 17.4: Radiation cascade for a three-level atom.
The spectral distribution is |φ
1
|
2
. Since
2
is small, the variation from f
12
can be
ignored to obtain
|φ
1
(k,λ)|
2
∼
=
C
(ε
2
+
2
− ε
1
−
1
− ω)
2
+ (
2
/2)
2
−1
= I (ω,
k,λ)
(17.84)
with the constant C =|f
12
(k,λ)|
2
evaluated at ω(k) = ε
2
− ε
1
, C = e
2
|ϕ(ε
2
−
ε
1
)|
2
((ε
2
− ε
1
)/2)|1|x|2·e
λ
(k)|
2
, which depends on the direction of emission,
k = k/|k|, and on the polarization. As a function of the frequency ω of the emitted
light, the line shape is Lorentzian of natural width
2
and centered at ε
2
+
2
−
ε
1
−
1
, differing from the bare line ε
2
− ε
1
by the shift
2
−
1
.
If the initial state of the atom is c
1
|1+c
2
|2, normalized as |c
1
|
2
+|c
2
|
2
= 1,
then φ = (c
1
, c
2
φ
1
(k
1
,λ
1
), 0,...).With probability |c
1
|
2
no photon is emitted
and with probability |c
2
|
2
the line shape is that of (17.84).
(ii) Three-level atom.Weconsider three nondegenerate levels |1, |2, |3 with
resonance poles z
j
= ε
j
+
j
− i
j
/2, j = 1, 2, 3,
1
= 0. The initial state of
the atom is |3. There is a direct transition |3→|1 as in case (i). In ad-
dition we have the cascade |3→|2→|1. Therefore the scattering state is
φ = (0,φ
1
,φ
2
, 0,...), see figure 17.4. φ
1
is as in (17.82) with label 2 replaced
by label 3. For the cascade one obtains

268 Radiation
φ
2
(k
1
,λ
1
, k
2
,λ
2
) = S
3
/2 + i(ε
3
+
3
− ε
1
−
1
− ω(k
1
) − ω(k
2
))
−1
×
2
/2 + i(ε
2
+
2
− ε
1
−
1
− ω(k
2
))
−1
×
√
2 f
12
(k
2
,λ
2
) f
23
(k
1
,λ
1
)
(17.85)
with S denoting symmetrization. If the variation and the direction dependence
from f
12
, f
23
are ignored, the intensity distribution for the two photons in the
cascade is
I (ω
1
,ω
2
) = C
4(
2
/2)
2
+ (δ
2
− ω
1
+ δ
2
− ω
2
)
2
×
(
3
/2)
2
+ (δ
2
+ δ
3
− ω
1
− ω
2
)
2
(
2
/2)
2
+(δ
2
− ω
1
)
2
(
2
/2)
2
+ (δ
2
− ω
2
)
2
−1
(17.86)
with the shorthand δ
3
= ε
3
+
3
− ε
2
−
2
,δ
2
= ε
2
+
2
− ε
1
−
1
.Ifε
3
−
ε
2
= ε
2
− ε
1
, then in the frequency spectrum one will observe a Lorentzian at δ
2
with natural width
2
and a Lorentzian at δ
3
with natural width
2
+
3
.Onthe
other hand if ε
3
− ε
2
= ε
2
− ε
1
and, just as an example, also
2
=
3
,2
2
=
3
,
then
I (ω
1
,ω
2
) = C
(
2
/2)
2
+ (δ
2
− ω
1
)
2
−1
(
2
/2)
2
+ (δ
2
− ω
2
)
2
−1
, (17.87)
which corresponds to a single Lorentzian at δ
2
= δ
3
of natural width
2
with dou-
ble intensity. The two photons interfere when emitted. Otherwise, the intensity
would be the sum of a Lorentzian of natural width
2
and one of natural width
2
+
3
= 3
2
.Ifε
3
− ε
2
∼
=
ε
2
− ε
1
, the exact intensity distribution (17.86) has
to be analyzed anew.
17.5 Scattering theory
From a very general perspective scattering theory is a comparison between an
interacting dynamics and a simplified “free” dynamics in the limit of long times.
In our context this means a study of
e
−iHt
ψ as t →∞ (17.88)
for an arbitrary initial state ψ ∈
H = C
N
⊗ F.Westay within the dipole approx-
imation and consider
H = H
at
+ H
f
− eQ · E
ϕ
, (17.89)
E
ϕ
= E
ϕ
(0). Since the coupling is fixed, we omit the index λ and return to e =
−λ, see (17.10). Also, ·, · always denotes the scalar product in
H. From the
outset we state
17.5 Scattering theory 269
Condition 17.3 (Uniqueness and localization of the ground state). H has a
unique ground state ψ
g
,Hψ
g
= E
g
ψ
g
with the property that ψ
g
, e
δN
f
ψ
g
< ∞
for some δ>0.Hhas no other eigenvalues.
On physical grounds it is easy to conjecture the limit in (17.88). Photons are
traveling outwards according to a scattering state φ and the atom decays to its
ground state ψ
g
. Thus for given ψ ∈ C
N
⊗ F, there exists a φ ∈ F such that
e
−iHt
ψ
∼
=
e
−iE
g
t
ψ
g
⊗
s
e
−iH
f
t
φ as t →∞. (17.90)
In rough terms, the state e
−iH
f
t
φ lives far away from the ground state ψ
g
.Still,
the bound photons of ψ
g
must be properly symmetrized with the freely propagat-
ing photons of e
−iH
f
t
φ. This is achieved by the symmetrization ⊗
s
as defined in
(17.91), (17.92) below. We note that in the previous sections we have discussed
an initial state of the particular form χ ⊗ . The relation (17.90) constitutes a
vast generalization thereof. Of course, the limit (17.90) can be considered also for
t →−∞. Combining both limits then yields the S-matrix for Rayleigh scattering
of photons from an atom.
To establish the limit (17.90) in this generality is a tough analytical problem,
since no exceptions are allowed. The limit is supposed to hold for all states ψ ∈
H.
We will only outline the general framework, in particular the proper definition of
the wave operators and their intertwining between the free and interacting dynam-
ics. As an easy step a Cook-type argument is established ensuring (17.90) at least
for a large class of states. One important consequence of the limit (17.90) is the
relaxation of the atom to its ground state without taking recourse to weak coupling,
respectively resonance theory. As will be explained, such a relaxation holds also
for local field observables.
Let us first have a look at the right-hand side of (17.90). The symmetrization ⊗
s
can be defined for two arbitrary states in Fock space. We consider the Fock space
F = F(h) over the one-particle space h. Then F(h ⊕ h) = F(h) ⊗ F(h).Onthe
one-particle space we define the map
(u
1
, u
2
) → u
1
+ u
2
∈ h. (17.91)
The second quantization of this map defines ψ
1
⊗ ψ
2
∈ F(h) ⊗ F(h) → ψ
1
⊗
s
ψ
2
∈ F(h). More explicitly, one has
n
j=1
a
∗
( f
j
)
⊗
s
m
i=1
a
∗
(g
i
)
=
n
j=1
a
∗
( f
j
)
m
i=1
a
∗
(g
i
). (17.92)
270 Radiation
In our case one factor is the ground state ψ
g
which can be thought of as a spinor-
valued vector in
F.Wethen define J : F → C
N
⊗ F through
J φ = ψ
g
⊗
s
φ, (17.93)
since ψ
g
is considered as given. If φ is an n-photon vector, φ =
(0,... ,φ
n
, 0,...), then
(ψ
g
⊗
s
φ)
n+j
=
n + j
n
1/2
Sψ
g j
φ
n
, (17.94)
with S denoting the symmetrizer.
As can be seen from (17.91), the symmetrization ⊗
s
is unbounded. In particular,
J φ
2
=
∞
n=0
n
i=0
n
j=0
n
i
1/2
n
j
1/2
Sψ
gi
φ
n−i
, Sψ
g j
φ
n−j
≤
∞
n=0
n
j=0
n
j
1/2
ψ
g j
φ
n−j
2
≤
∞
n=0
n
j=0
n
j
φ
n−j
2
e
−δj
n
i=0
ψ
gi
2
e
δi
. (17.95)
Let us define D
δ
={φ |φ
n
≤c(1 − e
−δ/2
)
n
}. Then for φ ∈ D
δ
,wehave
J φ < ∞, which is the reason for assuming the exponential bound in condi-
tion 17.3. Without it, we would have to go into details in what sense φ is far away
from the atom.
If the state φ shifted to infinity, either by the spatial shift e
−iw·P
f
or by the time
shift e
−iH
f
t
, then only the coupled ground state remains in focus. To see this on
a more formal level, we introduce the strictly local Weyl algebra
W
R
consisting
of operators of the form W ( f ) = exp[a
∗
( f ) − a( f )] with f (x,λ)= 0 for |x|≥
R. The quasi-local Weyl algebra
W is the norm closure of ∪
R>0
W
R
. The local
character is of importance, e.g. g(H
f
) with g bounded is obviously a bounded
operator, but g(H
f
) does not lie in W. Let A ∈ B(C
N
) ⊗ W. Shifting to infinity
then
lim
|w|→∞
ψ
g
⊗
s
e
−iw·P
f
φ, Aψ
g
⊗
s
e
−iw·P
f
φ=ψ
g
, Aψ
g
φ,φ
F
, (17.96)
lim
|t|→∞
ψ
g
⊗
s
e
−iH
f
t
φ, Aψ
g
⊗
s
e
−iH
f
t
φ=ψ
g
, Aψ
g
φ,φ
F
(17.97)
for all φ ∈ D
δ
.
To prove (17.96), (17.97), we choose an n-photon state of the form φ =
(0,... ,φ
n
, 0,...) with φ
n
(x
1
,λ
1
,... ,x
n
,λ
n
) = S
n
j=1
f
j
(x
j
,λ
j
),inother
17.5 Scattering theory 271
words φ = (n!)
−1/2
n
j=1
a
∗
( f
j
).Weset f
jw
(x
j
,λ
j
) = f
j
(x
j
− w, λ
j
) and
similarly
f
jt
(k
j
,λ
j
) = e
−iω(k
j
)t
f
j
(k
j
,λ
j
). Equations (17.96) and (17.97) go in
parallel and we consider only the latter. Then, for M ∈ B(
C
N
), W ( f ) ∈ W, and
since W ( f )a
∗
( f
j
) = a
∗
( f
j
)W ( f ) −f, f
j
h
W ( f ),weget
J e
−iH
f
t
φ, M ⊗ W ( f )J e
−iH
f
t
φ
=
1
n!
n
j=1
a
∗
( f
jt
)ψ
g
, M ⊗ W ( f )
n
j=1
a
∗
( f
jt
)ψ
g
=
1
n!
n
j=1
a
∗
( f
jt
)ψ
g
,
n
j=1
a
∗
( f
jt
)M ⊗ W ( f )ψ
g
+
1
n!
⊂{1,...,n},=∅
j∈
−f, f
jt
h
n
j=1
a
∗
( f
jt
ψ
g
,
j∈
c
a
∗
( f
jt
)Mψ
g
.
(17.98)
Since f is local, by the Riemann–Lebesgue lemma, lim
t→∞
f, f
jt
h
= 0. Simi-
larly, for space translations, lim
|w|→∞
f, f
jw
h
= 0. Therefore each term having
at least one contraction vanishes in the limit t →∞, respectively |w|→∞.We
still have to discuss the first summand corresponding to zero contraction which
written out explicitly is
∞
j=0
n + j
n
Sψ
g j
φ
nt
, S(M ⊗ W ( f )ψ
g
)
j
φ
nt
, (17.99)
by using (17.94) and setting φ
nt
= (e
−iH
f
t
φ)
n
. There are two types of terms in
the scalar product. If a φ
nt
is integrated either against ψ
g j
or against (M ⊗
W ( f )ψ
g
)
j
, then all such terms vanish as t →∞,again by the Riemann–Lebesgue
lemma. The only terms which survive in the limit are of the form ψ
g j
,(M ⊗
W ( f )ψ
g
)
j
φ
nt
,φ
nt
F
=ψ
g j
,(M ⊗ W ( f )ψ
g
)
j
φ
n
,φ
n
F
by unitarity. We
conclude that the limit t →∞in (17.99) equals
∞
j=0
ψ
g j
,(M ⊗ W ( f )ψ
g
)
j
φ
n
,φ
n
F
=ψ
g
, M ⊗ W ( f )ψ
g
φ,φ
F
,
(17.100)
as claimed. To cover the general case one has to take suitable linear combinations
and uniform limits.
272 Radiation
With these preparations the limit in (17.90) can be formulated more concisely.
We define the wave operators
∓
through the strong limit
∓
φ = s − lim
t→±∞
e
i(H −E
g
)t
J e
−iH
f
t
φ. (17.101)
The existence of this limit will be shown for all φ ∈ D
δ
by a Cook estimate in
Proposition 17.6 below. But we first want to explore some consequences of our
definition.
In the usual definition of wave operators one projects onto the scattering states
of the comparison dynamics e
−iH
f
t
. This is not needed here because for φ = ,
the limit in (17.101) equals ψ
g
. The formulation (17.101) assumes that H has no
other bound state. If this had been the case, one would have to allow in (17.101)
for several atomic channels, corresponding to the possibility that the atom remains
in an excited state forever.
The wave operators
±
are isometries from F to C
N
⊗ F,ascan be seen from
∓
φ,
∓
φ= lim
t→±∞
J e
−iH
f
t
φ, J e
−iH
f
t
φ=φ,φ
F
(17.102)
by (17.97) for φ ∈ D
δ
.Bycontinuity this property extends to all of F.
±
inter-
twines between the free and interacting dynamics as
e
−i(H −E
g
)t
±
=
±
e
−iH
f
t
, (17.103)
which is an immediate consequence of the definition: for φ ∈ D
δ
one has
e
−iH
f
t
φ ∈ D
δ
and
−
φ = lim
s→∞
e
i(H −E
g
)(t+s)
J e
−iH
f
(t+s)
φ
= lim
s→∞
e
i(H −E
g
)t
e
i(H −E
g
)s
J e
−iH
f
s
e
−iH
f
t
φ
= e
i(H −E
g
)t
−
e
−iH
f
t
φ. (17.104)
Since D
δ
is dense in F, (17.103) holds. As a consequence, Ran
∓
are reducing
subspaces for H and H − E
0
restricted to Ran
∓
is unitarily equivalent to H
f
on
F.
As emphasized, the limit in (17.90) should not only hold for some states but for
all ψ ∈
C
N
⊗ F.Itisuseful to have a name for such a property.
Definition 17.4
±
are called asymptotically complete if
Ran
±
= C
N
⊗ F. (17.105)
If
±
are asymptotically complete, then they are unitary and diagonalize H as
(
±
)
−1
(H − E
g
)
±
= H
f
. (17.106)
