Сорока Н.И., Кривинченко Г.А. Теория передачи информации

Подождите немного. Документ загружается.

Для преобразования дискретной функции в непрерывную нужно включить

идеальный фильтр частот с частотой среза равной F

max

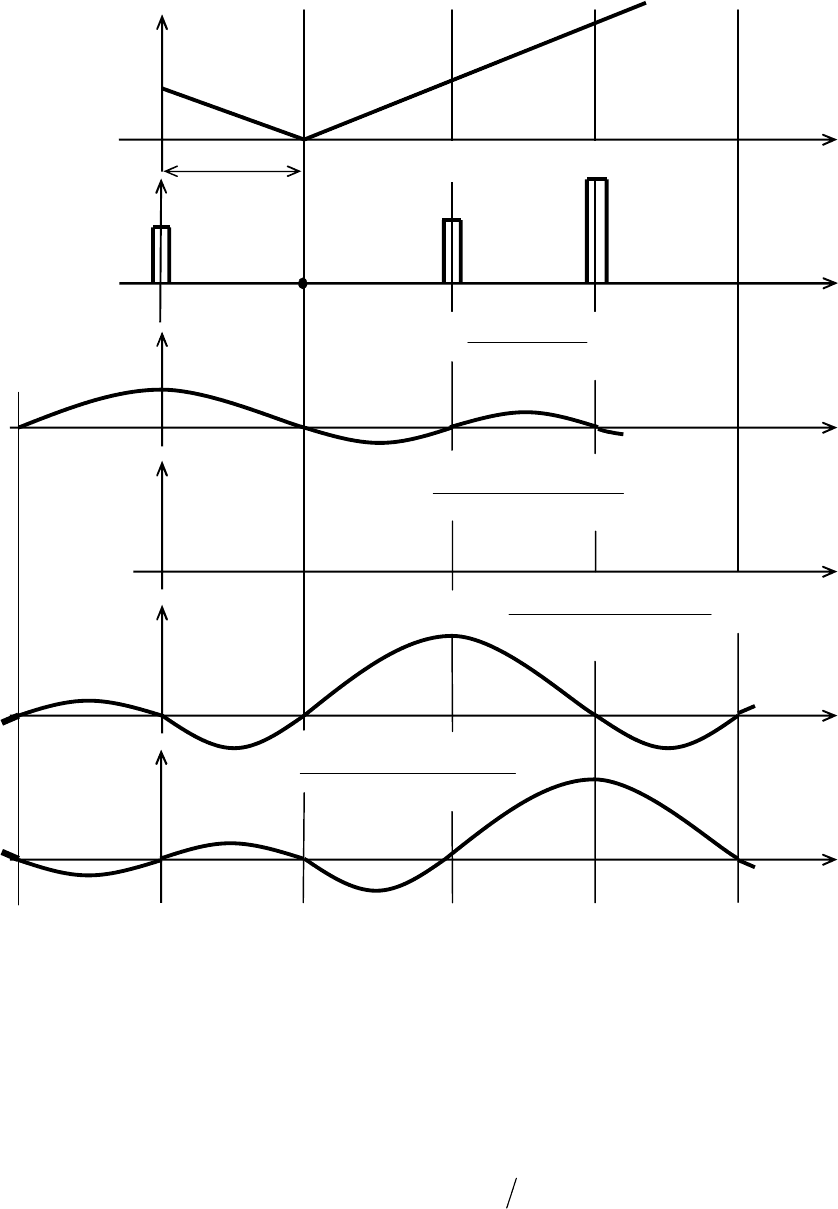
Рис. 1.12. Разложение функции f(t) с ограниченным спектром

частот по В.А.Котельникову

Рассмотренный процесс преобразования непрерывного сообщения в дис-

кретный во времени сигнал называется дискретизацией во времени.

В заключение следует отметить, что при определении на практике интер-

вала дискретизации теорему Котельникова можно применять с поправкой

)2(1

max

»D

, (1.33)

(t)

(0)

(Dt)

(2Dt)

(3Dt)

f (2

2Dt

(0)

(2D

sin2πF

max

(t-3∆t)

f(3 t)

2πF

max

(t-3∆t)

sin2πF

max

(t-2∆t)

2πF

max

(t-2∆t)

sin2πF

max

(t-∆t)

2πF

max

(t-∆t)

sin2πF

max

2πF

max

где h – коэффициент, зависящий от точности воспроизведения функции и

способа интерполяции; при линейной интерполяции

отнл

d=h 75,0 , при сту-

пенчатой

лст

)53( (относительная погрешность воспроизведения).

1.5.2. Дискретизация двумерной функции.

Все большую часть передаваемых по линии связи сообщений, составляют

сигналы, являющиеся функциями не только времени - λ(t) (речь, музыка и т.п.),

но и ряда других переменных, например, λ(x,y), λ(x,y,t) ( статические и динами-

ческие изображения, карты физических полей и т.п.). В связи с этим естествен-

ным является вопрос: можно ли так, как это делается для временных сигналов

(или других функций одной переменной), производить дискретизацию много-

мерных сигналов (функций нескольких переменных)?

Ответ на этот вопрос дает теорема дискретизации для двумерных (или в

общем случае - для многомерных) сигналов, которая утверждает: функция двух

переменных λ(x,y), двумерное преобразование Фурье которой

dxdyyfjxfjyxyxFF yx )2exp()2exp(),()},({ ****

ppll

--=

òò

+¥

¥-

(1.34)

равно нулю при f

≥ f

max и f

≥ f

max, однозначно определяется своими зна-

чениями в равноотстоящих точках плоскости переменных x и y, если интервал

дискретизации удовлетворяет условию Δx ≤ 1/2f

max , Δy ≤ 1/2f

. Процедура

дискретизации двумерной функции иллюстрируется примером, приведенным

на рис. 1.13.

Доказательство двумерной теоремы дискретизации основано, так же как и

для одномерного случая, на однозначном соответствии между сигналами и их

спектрами: одинаковым изображениям (двумерным функциям) соответствуют

одинаковые спектры, и наоборот, если спектры двух функций одинаковы, то и

сами эти функции равны друг другу.

Преобразование Фурье (спектр) дискретизованной двумерной функции

FF{λ(i

x,j

y)} получается периодическим продолжением спектра исходной не-

прерывной функции λ (x,y) в точки частотной плоскости (k

) (рис. 1.14),

где f

и f

- так называемые "пространственные частоты", являющиеся аналога-

ми обычной "временной" частоты и отражающие скорость изменения двумер-

ной функции λ (x,y) по соответствующим координатам (крупные фрагменты

изображения - низкие частоты, мелкие детали - высокие частоты).

Аналитически это можно записать следующим образом:

.)flf,fkf(y/x/)}yj,xi({FF

l k

yyxx*

åå

-¥=

--=

DDlDDDDl

11 (1.35)

Из рис.1.8 видно, что если соблюдается условие неперекрываемости пери-

одических продолжений спектра FF{λ(i

x,j

y)}, а это справедливо при

Δx≤1/2f

max , Δy ≤ 1/2f

max , то с помощью идеального двумерного ФНЧ с ча-

стотной характеристикой вида:

( )

( / ) ( / ) 12 , 12 ,

0 12 , 12

xxyyxy

Пf f Пf f , f / x f / y

H f f =

, f / x f / y

ì D D £D£D

³D³D

(1.36)

из спектра дискретизованной функции FF{λ(i

x,j

y)} можно абсолютно точно

выделить спектр исходной непрерывной функции FF{λ(x,y)} и, следовательно,

восстановить саму функцию.

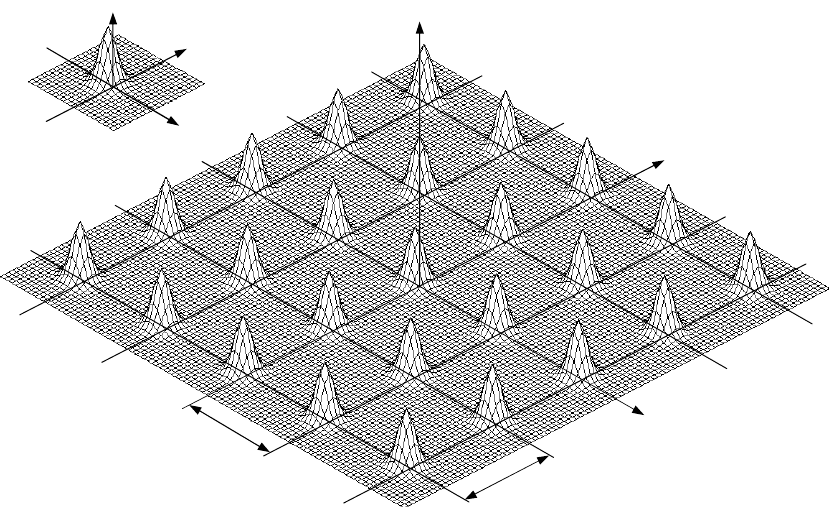
Рис.1.13. Процедура дискретизации двухмерных изображение: а - исходное

изображение; б - дискретизация по осям x и y; в – дискретизированное изображение.

Таким образом, видно, что не существует принципиальных отличий в дис-

кретизации между одномерными и двумерными (многомерными) функциями.

Результатом дискретизации в обоих случаях является совокупность отсчетов

функции, различия могут быть лишь в величине шага дискретизации, числе от-

счетов и порядке их следования.

Рис. 1.14 Спектр дискретизированной двухмерной функции.

1.5.3. Квантование сообщений по уровню и по времени. Ошибки кван-

тования.

Итак, показано, что передачу практически любых сообщений λ(t) ({λ(x,y)})

можно свести к передаче их отсчетов, или чисел λ

= λ(i

t), следующих друг за

другом с интервалом дискретности

1/2F

( Δx ≤ 1/2f

, Δy ≤ 1/2f

). Тем са-

мым непрерывное (бесконечное) множество возможных значений сообщения

λ(t) заменяется конечным числом его дискретных значений {λ(i

t)}. Однако са-

ми эти числа имеют непрерывную шкалу уровней (значений), то есть принад-

лежат опять же континуальному множеству. Для абсолютно точного представ-

ления таких чисел, к примеру, в десятичной (или двоичной) форме, необходимо

теоретически бесконечное число разрядов. Вместе с тем на практике нет необ-

ходимости в абсолютно точном представлении значений λ

, как и любых чисел

вообще.

Во-первых, сами источники сообщений обладают ограниченным динами-

ческим диапазоном и вырабатывают исходные сообщения с определенным

уровнем искажений и ошибок. Этот уровень может быть большим или мень-

шим, но абсолютной точности воспроизведения достичь невозможно.

Во-вторых, передача сообщений по каналам связи всегда производится в

присутствии различного рода помех. Поэтому принятое (воспроизведенное) со-

общение (оценка сообщения

(t) или

) всегда в определенной степени отли-

1/Δx

1/Δy

чается от переданного, то есть на практике невозможна абсолютно точная пере-

дача сообщений при наличии помех в канале связи.

Наконец, сообщения передаются для их восприятия и использования полу-

чателем. Получатели же информации - органы чувств человека, исполнитель-

ные механизмы и т.д. - также обладают конечной разрешающей способностью,

то есть не замечают незначительной разницы между абсолютно точным и при-

ближенным значениями воспроизводимого сообщения. Порог чувствительно-

сти к искажениям также может быть различным, но он всегда есть.

С учетом этих замечаний процедуру дискретизации сообщений можно

продолжить, а именно подвергнуть отсчеты λ

квантованию.

1.5.4. Квантование по времени и по уровню.

При преобразовании аналоговой величины в код квантование осуществля-

ется с заданными шагами как по времени, так и по уровню.

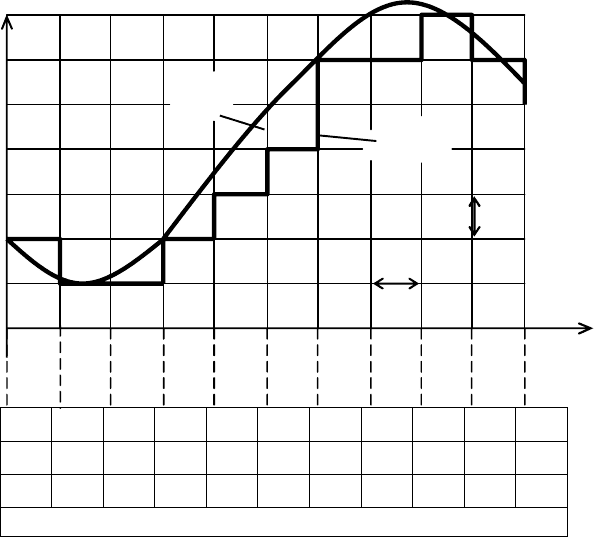
На рис. 1.15 показано, как производится квантование по уровню и по вре-

мени функции f(t). Сначала проводят линии, параллельные вертикальной оси

f(t) с шагом Dt, затем параллельные горизонтальной оси t с шагом q.

Квантование осуществляют заменой через шаг Dt значений функции f(t)

ближайшим дискретным уровнем. Этот уровень и является тем дискретным

значением, которое заменяет значение функции в данный дискретный момент

времени.

Если необходимо представить себе ступенчатую ломаную линию, которая

в результате квантования заменяет непрерывную функцию, все полученные

точки следует соединить так, как сделано на рис. 1.15.

2 1 1 2 3 4 6 6 7 6 5

Цифровой эквивалент

Рис. 1.15. Преобразование непрерывной величины в код

f (t)

f(t)

(t)

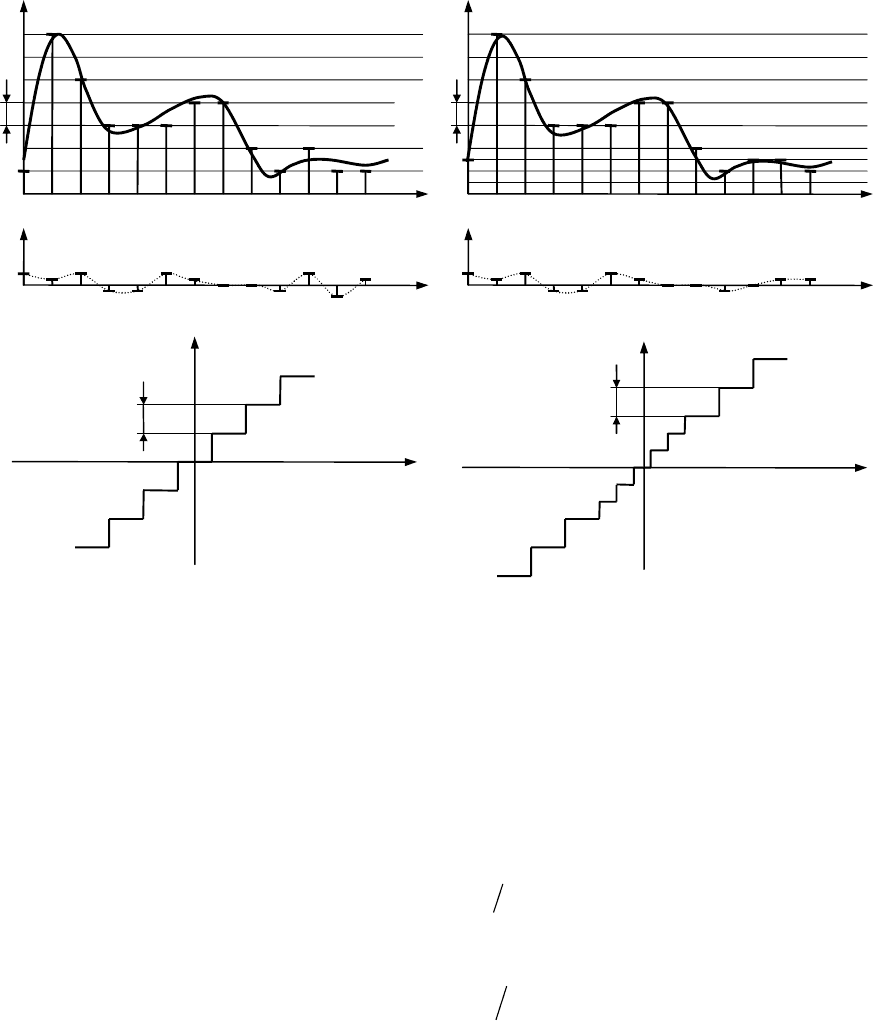
Различают равномерное и неравномерное квантование. В большинстве

случаев применяется и далее подробно рассматривается равномерное квантова-

ние (рис. 1.16), при котором шаг квантования постоянный: q = f

- f

i-1

= const;

однако иногда определенное преимущество дает неравномерное квантование,

при котором шаг квантования q

разный для различных f

(рис. 1.17).

Рис. 1.16. Квантование по уровню

равномерное: а - процесс квантования; б -

погрешность квантования; в - характери-

стика квантования.

Рис. 1.17. Квантование по уровню не-

равномерное: а - процесс квантования; б - по-

грешность квантования; в - характеристика

квантования.

Квантование приводит к искажению сообщений. Так как наименее точно

функция передается в точке, находящейся между двумя уровнями квантования

и отстоящей от них на половину интервала квантования q/2, то максимальная

ошибка квантования по уровню

, (1.37)

а мощность шума квантования при равномерном квантовании

P =

(1.38)

При достаточно большом числе уровней квантования N распределение по-

грешности квантования в пределах от – q/2 до + q/2 будет равномерным незави-

q(f)

ξ(t) ξ(t)

qΔ(f)

+N/2

-1

-2

-N/2

f(t)

симо от закона распределения самой функции f(t). Среднеквадратичное значе-

ние погрешности квантования по уровню

)32(q

ск

, (1.39)

т.е. в

3 раз меньше максимальной.

Что касается точности преобразования (квантования), то обычно она за-

дается в виде приведенной относительной погрешности

отн

в процентах. По

определению,

))()(()100(%

minmax

tftf

отн

-×D=

. Подставив значение D из (1.37),

получим выражение для шага квантования при

0)(

min

=tf

100)(2

max отн

tfq

. (1.40)

После того как непрерывное сообщение с помощью квантования будет

преобразовано в дискретное сообщение, необходимо каждому его уровню при-

своить цифровой эквивалент, как правило, в двоичном неизбыточном коде (см.

рис. 1.15) и передать по каналу связи. При этом, если известен шаг квантования

q, то число уровней квантования N и число разрядов кодовой комбинации K при

0)(

min

=tf

можно определить из выражения

12/)(

max

-==

qtfN

. (1.41)

Пример 1. Предположим, что необходимо произвести квантование непре-

рывной функции, изменяющейся от нуля до 100 В, с точностью

ск

= 1%. Опре-

делить величину шага квантования, число уровней квантования и число разря-

дов кодовой комбинации. Согласно (1.40),

В. Из (1.41) определим, что

необходимо 50 уровней квантования, а число разрядов

651log

. Такое

число уровней устанавливается, если измерение в данной точке производят до

ближайшего уровня (нижнего или верхнего). При схемной реализации отсчет

часто производят до какого-нибудь одного уровня (только нижнего или только

верхнего). В этом случае для обеспечения точности квантования в 1% от 100 В

число уровней следует взять 100, так как

100/)(

max отн

tfq

==D

, а следова-

тельно k = 7.

Контрольные вопросы

1. Какой сигнал называется регулярным?

2. Запишите выражение для периодичного сигнала.

3. Какой сигнал называется не периодическим?

4. Приведите временную диаграмму для дискретного сигнала.

5. Запишите ряд Фурье для периодичного сигнала.

6. Что означает представление сигнала с заданным периодом рядом

Фурье?

7. Приведите спектр периодически повторяющихся прямоугольных им-

пульсов.

8. Приведите выражение для средней мощности периодических прямо-

угольных импульсов.

9. Что понимается под практической шириной спектра сигнала?

10. Приведите форму сигнала при ограничении спектра прямоугольных

импульсов, имеющих скважность Q =3 и ограниченных третьей гармонической

составляющей.

11. Приведите выражение для спектра непериодического сигнала.

12. Поясните график зависимости энергии импульсов от ширины сохра-

няемой части спектра.

13. Сформулируйте теорему В.А. Котельникова о преобразовании непре-

рывных сообщений в дискретные сигналы.

14. Сформулируйте теорему дискретизации для двумерных сигналов.

2. КОЛИЧЕСТВЕННАЯ ОЦЕНКА ИНФОРМАЦИИ

2.1. Количество информации при равновероятности состояний

источника сообщений

Сообщения разнятся как по своей природе, так и по содержанию и по

назначению. В связи с этим возникают трудности в оценке количества инфор-

мации, которое содержится в сообщениях. Количество информации должно

определяться через нечто общее, объективно присущее всему многообразию

различной информации, оставаясь при этом созвучным нашим интуитивным

представлениям, связанным с фактом получения информации. Этим общим, ха-

рактеризующим фактом получения произвольной информации, является, во-

первых, наличие опыта. Всякая информация добывается нами в результате

опыта и только опыта. Во-вторых, до опыта должна существовать некоторая

неопределенность в том или ином исходе опыта.

Таким образом, до опыта всегда имеется большая или меньшая неопреде-

ленность в интересующей нас ситуации. После опыта ситуация становится бо-

лее определенной и на поставленный вопрос мы можем ответить либо одно-

значно, либо число возможных ответов уменьшится и, следовательно, умень-

шится существовавшая ранее неопределенность. Количество уменьшенной не-

определенности после опыта, очевидно, можно отождествить с количеством

получаемой информации в результате опыта.

Теперь ясно, что для установления формулы для вычисления количества

информации необходимо уметь вычислять неопределенность некоторой ситуа-

ции до и после опыта. Разность между этими количествами неопределенности и

дает нам искомое количество информации, полученное от такого опыта.

К количеству информации (неопределенности до опыта) можно предъ-

явить три интуитивных требования.

1. Количество получаемой информации больше в том опыте, у которого

большее число возможных исходов.

Обозначая количество информации буквой I, а число возможных исходов

n, первый постулат запишем в виде:

),()(

nInI

если .

(2.1)

2. Опыт с единственным исходом несет количество информации, равное

нулю, т.е.

)

(

(2.2)

3. Количество информации от двух независимых опытов равно сумме ко-

личества информации от каждого из них:

).()()(

2121

nInInnI

(2.3)

Очевидно, единственной функцией аргумента n, удовлетворяющей трем

поставленным условиям, является логарифмическая. Итак, количество инфор-

мации от опыта с N исходами при условии, что после опыта неопределенность

отсутствует:

.log

NCI

(2.4)

Выбор постоянной С и основания логарифмов здесь несущественен, так

как определяет только масштаб на единицу неопределенности. Поэтому поло-

жим С = 1, а = 2. Тогда

log

(2.5)

Указанная мера была предложена Р. Хартли в 1928г. для количественной

оценки способности системы хранить или передавать информацию.

Такая мера удовлетворяет требованию аддитивности. Емкость устройства

состоящего из n ячеек, имеющего N = m

состояний, равна емкости одной ячей-

ки, умноженной на число ячеек:

.loglog mnmC

== (2.6)

За единицу измерения емкости принята двоичная единица или bit, равная

емкости одной ячейки с двумя возможными состояниями.

Следует отметить, что мера количества информации в виде (2.6) относится

к весьма частному случаю, когда после опыта неопределенности в исходе нет и

все исходы равновероятны.

Дальнейшее развитие теории информации шло в направлении учета стати-

стических характеристик.

Если от источника информации по каналу связи передавать сообщение о

событии, априорная вероятность которого на передающей стороне равна Р

, то

после приема сообщения апостериорная вероятность этого события для прием-

ника информации равна Р

и количество информации, полученное в результате

приема сообщения, будет

.loglog)/log(

1212

PPPPI

(2.7)

Для канала связи без помех и искажений прием сообщения становится до-

стоверным событием, т.е. вероятность Р

= 1, тогда из (2.7) следует, что

.log

(2.8)

Из (2.8) следует, что чем меньше вероятность Р

, тем больше неопределен-

ность исхода, т.е. тем большее количество информации содержится в принятом

сообщении.

Значение Р

находится в пределах ,10

P следовательно,

logPI

всегда положительная величина.

Количество информации

log

, где Р – вероятность события, было

положено в основу и было исходной точкой создания теории информации.

2.2. Энтропия ансамбля

Ансамблем называется полная совокупность состояний с вероятностями их

появлений, составляющими в сумме единицу:

PPPP

XXXX

(2.9)

причем .1

Пусть имеет место N возможных исходов опыта, из них k разных, и i-й ис-

ход (i = 1, 2,..., k) повторяется n

раз и вносит информацию, количество которой

оценивается как I

. Тогда средняя информация, доставляемая одним опытом,

равна

2211

InInIn

СР

(2.10)

Но количество информации в каждом исходе согласно (2.8) будет

.log

(2.11)