Сологаев В.И. Прогнозы и моделирование подтопления и дренирования в городском строительстве

Подождите немного. Документ загружается.

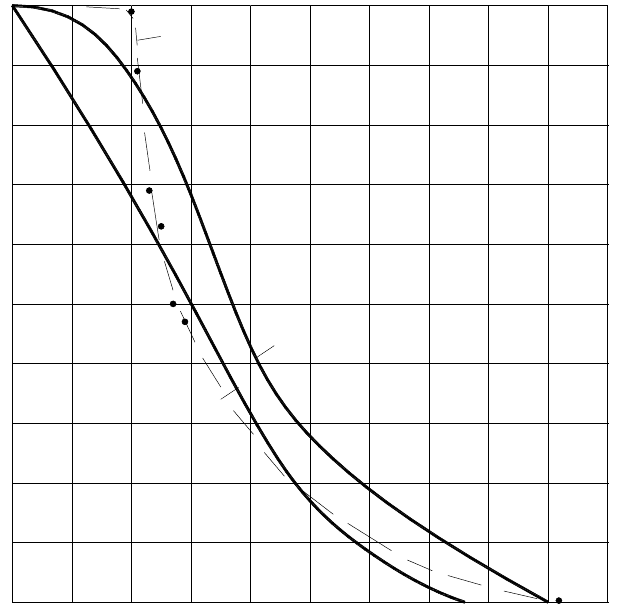
Рис. 4. Зависимость относительной фазовой проницаемости по воздуху от степени

влажности: 1 — для глинистых грунтов [204]; 2 — для песчаных грунтов [12; 111]; 3 —

опытная кривая с точками для неравномерно увлажненного песка (см. пример 31 в

[262])

Таким образом, автор по теме исследования:

— уточнил терминологию коэффициента водоотдачи;

— предложил использовать при моделировании коэффициент

водоотдачи по всему интервалу опробования водоносного пласта;

— указал, что прогнозы и моделирование фильтрационных процессов

в работе рассмотрены в рамках закона Дарси;

— привел экспериментальные результаты по воздухопроницаемости,

связанные с технологией водопонижения.

0,5

2.1.1. Дифференциальные уравнения фильтрации воды и воздуха

Приведем дифференциальные уравнения фильтрации воды, относя-

щиеся к целям нашей работы. Строго говоря, фильтрация воды в грунтах

всегда нестационарная, трехмерная, а скелет грунта имеет склонность к

деформации и анизотропии. Кроме того, в воде присутствует воздух, что

увеличивает ее сжимаемость [206] и уменьшает проницаемость пористой

среды [6; 7]. Однако на практике дифференциальные уравнения фильтра-

ции стремятся по возможности упростить. Так делают, чтобы получить не-

сложные аналитические решения в виде формул, а также при нефизиче-

ском моделировании. При этом опускают из рассмотрения не очень суще-

ственные особенности процесса фильтрации.

Классификация дифференциальных уравнений фильтрации построена с

учетом основных трудов по теории фильтрации [206]. Эти уравнения в

свое время классифицировали С.Ф. Аверьянов [6; 7], В.И. Аравин и С.Н.

Нумеров [12], Я. Бэр и С. Ирмей [38], Н.Н. Веригин [39; 147], И.К. Гавич

[48; 49], Н.П. Куранов [48; 113, ], В.А. Мироненко [148], А.Ж. Муфтахов

[152], Н.Н. Павловский [182; 183], П.Я. Полубаринова-Кочина [194; 195],

В.С. Усенко [289], В.М. Шестаков [313].

В наиболее общем виде с физическим смыслом дифференциальные

уравнения фильтрации вывел и опубликовал в 1922 г. Н.Н. Павловский

[183].

Н.Н. Павловский [183], с учетом вышеизложенных представлений и

обстоятельств, указал, что гидромеханический смысл модели фильтрации

необходим для вывода дифференциальных уравнений движения.

Н.Н. Павловский, используя формулу М.В. Остроградского — Д. Гри-

на, получил наиболее общее дифференциальное уравнение неразрывности

для фильтрующейся сжимаемой жидкости в деформируемой пористой

среде [183]:

( 7)

с характеристическими уравнениями, выражающими зависимости плотно-

сти жидкости от давления

( 8)

и пористости среды от давления

( 9)

Здесь V

, V

— компоненты вектора скорости фильтрации соот-

ветственно вдоль декартовых осей координат X, Y, Z, где Z — вертикаль-

ная ось; t — время; x, y, z — координаты точки.

При постоянной плотности жидкости (



= const), Н.Н. Павловский

[183] получил такой вариант уравнения неразрывности:

( 10)

которое при постоянной пористости (n = const), то есть при несжимаемой

пористой среде переходит в уравнение [183]

( 11)

где коэффициент фильтрации переменный и имеет общую зависимость

( 12)

Уравнение ( 11) можно записать короче как дивергенцию вектора ско-

рости фильтрации в виде

( 13)

Для однородной изотропной несжимаемой пористой среды (k = const,

n = const) из уравнения (22) получается уравнение Лапласа, где функцией

является фильтрационный напор [183]:

( 14)

 





   

x z

x y z t

 

     

   

   

V V



= f(p)

n = f(p).

H H H n

k k k

x x y y z z t

      

     

  

     

     

H H H

k k k

x x y y z z

     

     

  

     

     

k = f(x, y, z),

div 0.



2 2 2

0 ,

H H H

x y z

  

  

которое можно переписать в сокращенном виде

( 15)

где 

— оператор Лапласа (лапласиан) [103, с. 173; 64, с. 482].

Уравнение ( 11) пригодно для описания стационарной напорной и без-

напорной фильтрации несжимаемой воды в недеформируемой пористой

среде. Оно описывает также и нестационарную жесткую фильтрацию без-

напорных потоков со свободной поверхностью. Для этого должно быть

добавлено условие на свободной поверхности, например на УГВ. Вообще,

при наличии зависимости скорости фильтрации от вертикальной коорди-

наты z, уравнение ( 11) относится к так называемой гидродинамической

теории фильтрации. Термин «гидродинамическая теория фильтрации»

введен П.Я. Полубариновой-Кочиной [194].

Уравнением Буссинеска называют дифференциальное уравнение

фильтрации воды со свободной поверхностью, не зависящее от вертикаль-

ной координаты z. Это означает, что уравнение Буссинеска связывают с

так называемой гидравлической теорией фильтрации применительно к

грунтовым водам и верховодке на водоупорах. Именно в этом смысле в

дальнейшем изложении применяется термин «уравнение Буссинеска».

Гидравлическую теорию фильтрации начали применять еще в XIX веке

Ж. Дюпюи, Ж. Буссинеск и Ф. Форхгеймер. Эта теория рассматривает

фильтрацию, направление которой близко к горизонтальному. При изуче-

нии грунтовых потоков воду и пористую среду считают несжимаемыми.

Такую фильтрацию называют жесткой [39].

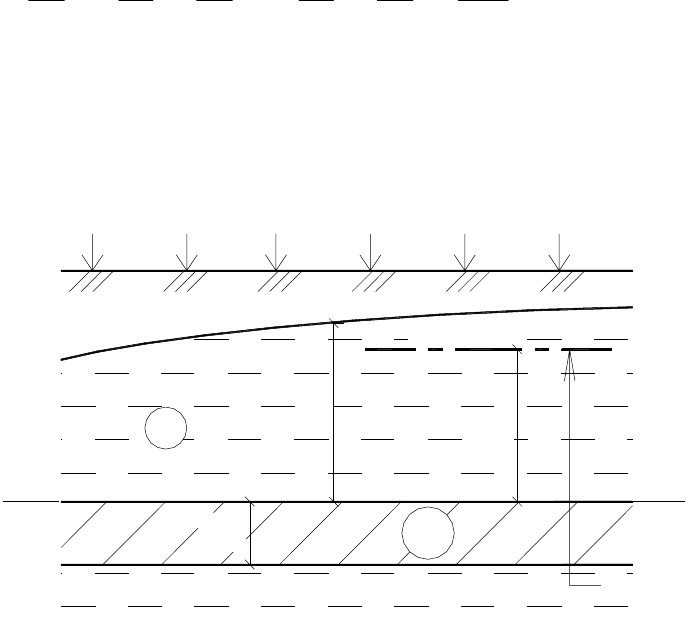
Обобщенное уравнение Буссинеска имеет вид [206] (рис. 5):





     

0 0

H H

k H z k H z H H

t x x y y M

 

  



    

   

      

   

   

( 16)

где H — вертикальная отметка (напор) свободной поверхности УГВ от го-

ризонтальной плоскости отсчета напоров 0-0; х, у — декартовы координа-



H = 0 ,

ты в горизонтальной плоскости;



— гравитационная гидроемкость по

(12); z

— отметка подошвы слабопроницаемого водоупора относительно

плоскости 0-0; (H  z

) — мощность грунтовых вод (h); t — время; k

—

коэффициент фильтрации слабопроницаемого водоупора мощностью M

(см. рис. 4); H

— напор в напорном пласте под водоупором (см. рис. 4);



— инфильтрационное питание грунтовых вод (может быть также с учетом

испарения). Напомним, что все напоры отсчитывают от единой плоскости

сравнения 0-0 (см. рис. 5).

0 0

УГВ

УНПВ

Ур.з.



H H

Рис. 5. К обобщенному уравнению Буссинеска (28)

Уравнение Буссинеска ( 16) с математической точки зрения является

нелинейным, так как имеет переменные коэффициенты k и



. Кроме того,

переменными являются мощность грунтовых вод (H  z

), мощность во-

доупора M

, напор в нижележащих напорных водах H

и интенсивность

инфильтрации



. Это усугубляет нелинейность уравнения ( 16) поэтому

его в большинстве случаев невозможно решить аналитически. Получено

очень мало решений уравнения ( 16) для простейших одномерных задач

[206]. Однако нелинейное уравнение Буссинеска ( 16) можно промодели-

ровать с учетом всех переменных факторов.

Уравнение Буссинеска ( 16) справедливо для потоков грунтовых вод с

медленно изменяющейся неустановившейся фильтрацией [165]. В работе

[153] А.Ж. Муфтахов показал, что уравнение Буссинеска применимо для

практических расчетов, если величина инфильтрации



значительно

меньше коэффициента фильтрации грунта k. Должно соблюдаться условие

( 17)

Если поверхность водоупора горизонтальная или близка к таковой

(рис. 5), а водоносный грунт является однородным и изотропным, то нели-

нейное уравнение Буссинеска (28) можно упростить до вида [206]

( 18)

где h — одновременно напор и мощность грунтовых вод при горизонталь-

ной плоскости 0-0 отсчета напоров, совмещенной с водоупорной подошвой

(см. рис. 6). Остальные обозначения те же, что к уравнению ( 16).

Рис. 6. К упрощенному нелинейному уравнению Буссинеска

и линеаризованному уравнению по 2-му способу

Упрощенное уравнение Буссинеска ( 18) все равно остается нелиней-

ням, поэтому прибегают к его линеаризации [206] с целью получения ана-

литических зависимостей в виде формул. Линеаризацию уравнения ( 18)

можно применять, когда изменения поверхности УГВ h по отношению к



<< k.

 

h h h k

k h k h h H

t x x y y M

    

 

    

   

    

   

   





Ур.з.

УНПВ

УГВ

0 0

естественной мощности грунтовых вод h

не превышают 10-25 % [6; 7; 48;

152; 313], что дополнительно исследовано в п. 3.2.

Наиболее широко в мировой практике применяют два способа линеа-

ризации нелинейного уравнения Буссинеска (30) [206]:

— первый способ линеаризации (способ Ж. Буссинеска);

— второй способ линеаризации (по Н.А. Багрову и Н.Н. Веригину).

Рассмотрим 1-й способ линеаризации уравнения Буссинеска (способ по

Буссинеску). В уравнении ( 16) нужно заменить переменную мощность

грунтовых вод (H  z

) на постоянную среднюю мощность водоносного

пласта h

. Эта замена придает грунтовым водам сходство с напорными во-

дами, имеющими постоянную мощность М. Однако поверхность водоупо-

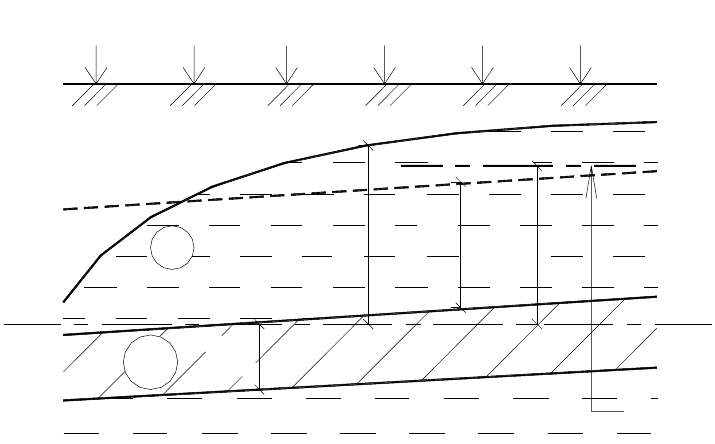
ра может иметь слабый уклон (рис. 7). Водоносный грунт принимают од-

нородным и изотропным. Тогда линеаризованное I способом уравнение

Буссинеска (28) можно переписать так [206]:

( 19)

где а

— коэффициент уровнепроводности грунтовых вод, м

/сут; Н —

напор свободной поверхности УГВ, отмеряемый от горизонтальной плос-

кости 0-0 (см. рис. 7). Остальные обозначения те же, что в уравнении ( 16).

Среднюю мощность безнапорного водоносного пласта h

надо прини-

мать такой, чтобы она обеспечивала наиболее достоверный расчет. Чаще

всего [204] величину h

принимают равной среднему арифметическому

минимальной h

min

и максимальной h

max

мощности водоносного пласта в

виде

( 20)

Другие, более точные способы определения h

изложены, например, в

[6; 44; 147; 201; 204]. Следует заметить, что при небольших изменениях

УГВ относительно мощности пласта (меньше 10—25 %) формула ( 20) да-

 

2 2

у c B c

H H H k

H H

a t x y kh M kh

   

  

    

= (h

max

+ h

min

)/2.

ет результаты в пределах инженерной точности.

Коэффициент уровнепроводности грунтовых вод а

— это комплекс-

ный параметр. Его находят по формуле:

( 21)

0 0

УГВ

УНПВ

Ур.з.



Рис. 7. Схема к линеаризации по 1-му способу

Линеаризацию уравнения Буссинеска ( 18) по 2-му способу предложи-

ли независимо друг от друга гидрометеоролог Н.А. Багров в 1937 году и

гидродинамик Н.Н. Веригин [40]. Эту линеаризацию применяют при гори-

зонтальном водоупоре (см. рис. 6). Суть линеаризации по II способу состо-

ит в подстановке вида

( 22)

что однако не избавляет от необходимости введения средней мощности

пласта безнапорных вод h

. Достоинством линеаризации по 2-му способу

является получение в стационарных задачах поверхности грунтовых вод в

виде выпуклой вверх параболы Дюпюи. В нестационарных задачах I и II

способы линеаризации конкурентоспособны. П.Я. Полубаринова-Кочина

[194; 195], а позднее Н.П. Куранов [114] показали, что в задачах подпора

УПВ более предпочтительным является I способ линеаризации, а в задачах

дренирования — II способ. В любом случае линеаризация является при-

= k h



U = H

/2 или U = H

ближенным приемом, который нужно проверять каждый раз независимым

способом, например моделированием.

Гидравлическая теория фильтрации хорошо описана в книгах П.Я. По-

лубариновой-Кочиной [194; 195]. Эта теория доминировала в практиче-

ском применении теории фильтрации в XIX-XX вв. В рамках гидравличе-

ской теории фильтрации работали:

— российские ученые Н.Е. Жуковский, Н.Н. Павловский, С.Ф. Аверья-

нов, В.И. Аравин, С.Н. Нумеров, Н.Н. Веригин, А.Ж. Муфтахов, Н.П. Ку-

ранов, Б.С. Шержуков, В.К. Рудаков, В.А. Мироненко, В.М. Шестаков и

многие другие;

— зарубежные ученые А. Дарси, Ж. Дюпюи, Ж. Буссинеск, А. Тим, Ф.

Форхгеймер и др.

Гидравлическая теория фильтрации остается до сих пор основной в

практических фильтрационных расчетах. Например, она широко использо-

вана в стандартных расчетах справочного пособия к СНиП [204].

В 1969-70 гг. Н.Н. Веригин [39; 147] предпринял дополнительные ис-

следования по анализу уравнений фильтрации подземных вод. Он получил

интересный результат: при гидрогеологических прогнозах на срок t  30

лет можно без существенных погрешностей в определении напора (ошибка

не более 5 %) использовать дифференциальное уравнение, аналогичное

уравнению теплопроводности (уравнению Фурье):

( 23 )

где a — коэффициент пьезопроводности или уровнепроводности в зависи-

мости от типа фильтрационного потока, соответственно, напорного или

безнапорного (со свободной поверхностью). При этом Н.Н. Веригин при-

вел и другое ограничительное условие применения уравнения ( 23):

а  10

/сут.

Оба условия, по времени прогноза t и коэффициенту а, практически не

ограничивают область применения дифференциального уравнения ( 23) в

a H



 

реальных пластах подземных вод. Это позволило Н.Н. Веригину с соавто-

рами [147] получить большое количество решений дифференциального

уравнения ( 23) при различных граничных условиях. Полученные в [147]

аналитические формулы относятся к линейной теории фильтрации или

гидравлической теории. Область применения этих зависимостей определе-

на авторами коллективной монографии [147] для фильтрационных расче-

тов гидромелиоративных систем сельского хозяйства. Следует отметить,

что многие решения из [147] применимы и для городского строительства

при условии, что величины изменения УГВ не превышают 10–25 % от ес-

тественной мощности грунтовых вод [6; 7; 48; 315].

А.Ж. Муфтахов получил общий класс аналитических решений для

уравнений в гидродинамической постановке, в изотропных и анизотроп-

ных пластах подземных вод [152]. Были разработаны гидродинамические

основы прогнозов подтопления промплощадок и фильтрационные расчеты

защитных дренажей в сложных гидрогеологических условиях. А.Ж. Муф-

тахов проанализировал свои решения для двухслойного в разрезе водонос-

ного пласта со свободной поверхностью УПВ. При этом А.Ж. Муфтахов

применил постановку задач в виде следующих систем дифференциальных

уравнений жесткой фильтрации [152]:

а) плоская в разрезе фильтрация

( 24 )

б) осесимметричная в разрезе фильтрация









0 1 2

r r

i i

    ; , ; ;

или [201]

( 25)

в) трехмерная фильтрация

2 2

0; 1, 2; ;

i i zi

i i

H H k

x z k

 

 

 

   

0 ;

i i

H H

r r r z

 



  

 

 

 

 