Скоробогатова В.И. Методические указания по теории вероятностей и математической статистике
Подождите немного. Документ загружается.


МИНИСТЕРСТВО НАУКИ и ОБРАЗОВАНИЯ УКРАИНЫ
Черниговский Государственный Технологический Университет
КАФЕДРА ЭЛЕКТРИЧЕСКИХ СИСТЕМ и СЕТЕЙ
М Е Т О Д И Ч Е С К И Е У К А З А Н И Я
ПО ТЕОРИИ ВЕРОЯТНОСТЕЙ и МАТЕМАТИЧЕСКОЙ
СТАТИСТИКЕ
Составитель: В. Скоробогатова
Чернигов - 2007
Методические указания составлены для студентов специальности
7.090602 «Электрические системы и сети». Цель их- оказание помощи
студентам заочной формы обучения, изучающим теорию вероятностей и
математическую статистику. Методические указания содержат
следующие разделы: классическое определение вероятности и ее свойства,
дискретные и непрерывные случайные величины. В тексте приводятся
наиболее часто встречающиеся утверждения и формулы, разобрано
большое количество задач.
СОДЕРЖАНИЕ
1. Некоторые формулы комбинаторики 4
2. Случайные события. Классическое определение вероятности 4
3. Относительная частота события. Статистическое определение
вероятности 7
4. Сложение вероятностей 7
5. Умножение вероятностей независимых событий 9
6. Зависимые события. Условная вероятность. Формула полной
вероятности 11
7. Формула Байеса 13
8. Формула Бернулли 14
9. Формула Пуассона 16
10. Случайные величины 17
11. Закон распределения дискретной случайной величины 17
12. Числовые характеристики дискретной случайной величины 18
13. Биномиальный закон распределения дискретной случайной
величины 20
14. Закон распределения Пуассона дискретной случайной величины 21
15.
Функция распределения непрерывной случайной величины.
Плотность распределения 21
16. Числовые характеристики непрерывной случайной величины 23
17. Закон равномерного распределения вероятностей непрерывной
случайной величины 25
18. Числовые характеристики равномерного распределения 26
19. Нормальный закон распределения непрерывной случайной
величины 27
20. Числовые характеристики нормального распределения 27
21. Функция Лапласа. Функция распределения случайной величины Х,
имеющей нормальное распределение 26
22. Вероятность попадания случайной величины Х, имеющей
нормальное распределение, в заданный интервал 28
23. Литература 30
Некоторые формулы комбинаторики
Рассмотрим некоторое множество Х, состоящее из n элементов
n
xxxX ,...,,
21
. Будем выбирать из этого множества различные
упорядоченные подмножества У из k элементов. Размещением из n
элементов множества Х по k элементам назовем любой упорядоченный
набор
k
iii
xxx ,...,,
21
элементов множества Х.
Если выбор элементов множества У из Х происходит с возвращением,
т.е. каждый элемент множества Х может быть выбран несколько раз, то число
размещений из n по k находится по формуле n
k
.
Если же выбор делается без возвращения, т.е. каждый элемент
множества Х можно выбирать только один раз, то количество размещений из
n по k обозначается
k
n
A
и определяется равенством
)1)...(1( knnnA
k
n
.
Например. Пусть даны пять цифр: 1; 2; 3; 4; 5. Определим сколько
трехзначных чисел можно составить из этих цифр. Если цифры могут
повторяться, то количество трехзначных чисел будет
1255
3
k
nm
.
Если цифры не повторяются, то
60345
3
5
Am
.
Частный случай размещения при n=k называется перестановкой из n
элементов. Число всех перестановок из n элементов равно
!nA
n
n
.
Пусть теперь из множества Х выбирается неупорядоченное
подмножество У, т.е. два подмножества У
1
и У
2
из k элементов, состоящие из
одних и тех же элементов и отличающиеся их порядком будем считать
одинаковыми. Сочетаниями из n элементов по k называются подмножества
из k элементов, отличающиеся друг от друга хотя бы одним элементом.
Общее число всех сочетаний из n по k обозначается
k
n
C
и равно
!
)1)...(1(
!)!(
!
! k
knnn
kkn
n
k
A
C
k
n
k
n
.
В дальнейшем будем считать
1
0
n
C
.
Заметим, что справедливо равенство
kn
n
k
n
CC
.
Например. В группе из 27 человек нужно выбрать трех делегатов на
профсоюзную конференцию. Вычислить количество всевозможных
профсоюзных делегаций.
2925
!3
252627
3
27
Cm
.
Случайные события.
Классическое вероятность
Основным понятием теории вероятностей является понятие случайного
события. Случайным событием называется событие, которое при
осуществлении некоторых условий может произойти или не произойти.
Например, попадание в некоторый объект или промах при стрельбе по этому
объекту из данного орудия является случайным событием.

Рассмотрим виды событий.
Событие называется достоверным, если в результате испытания оно
обязательно происходит.
Невозможным называется событие, которое в результате испытания
произойти не может.
Случайные события называются несовместными в данном испытании,
если никакие два из них не могут произойти вместе.
Случайные события образуют полную группу, если при каждом
испытании появится одно из них (любое), но не появится одновременно два
и более событий, т. е. События попарно несовместимы.
Рассмотрим полную группу равновозможных несовместных случайных
событий. Такие события будем называть случаями. Событие такой группы
называется благоприятствующим появлению события А, если появление
этого события влечет появление А.
Например, в урне находится 8 шаров, на каждом из которых поставлено
по одной цифре от 1 до 8. Шары с цифрами 1, 2, 3 красные, остальные –
черные. Появление шара с цифрой 1 (2 или 3) есть событие,
благоприятствующее появлению красного шара.
Вероятностью р события А называется отношение числа m
благоприятствующих случаев к числу всех возможных случаев n,
образующих полную группу равновозможных несовместных событий
n
m
pAP )(
.
Заметим, что вероятность достоверного события р=1. Вероятность
невозможного события р=0. Кроме того из определения вероятности следует,
что для любого события А
1)(0 AP
.
Примеры. 1. В урне 10 пронумерованных шаров с номерами от 1 до 10.
Вынули один шар. Какова вероятность того, что номер вынутого шара не
превосходит 10?
Пусть событие А – номер вынутого шара не превосходит 10. Число
случаев благоприятствующих появлению события А равно числу всех
возможных случаев m=n=10. Следовательно, Р(А)=1.
2. В урне 15 шаров: 5 белых и 10 черных. Какова вероятность вынуть из
урны синий шар?
Так как синих шаров в урне нет, то m=0, n=15. Следовательно, искомая
вероятность р=0.
3. Из колоды в 36 карт вынимается одна карта. Какова вероятность
появления карты пиковой масти?
Здесь всего случаев n=36. Событие А – появление карты пиковой масти.
Число случаев, благоприятствующих появлению события А, m=9.
Следовательно,
4
1
36
9
)( AP
.
4. Бросаются одновременно две монеты. Какова вероятность выпадения
герба на обеих монетах?

Составим схему возможных случаев.
Первая монета Вторая монета
1 случай
2 случай
3 случай
4 случай
герб
герб
не герб
не герб
герб
не герб
герб
не герб
Всего случаев 4. Благоприятствующих случаев 1. Следовательно, р=1/4.
5. В урне 10 шаров: 6 белых и 4 черных. Вынули два шара. Какова
вероятность, что оба шара белые?
Вынуть два шара из десяти можно следующим числом способов:
45
2
910
2
10
Cn
. Число случаев, когда среди этих двух шаров будут оба
белые, равно
15
2
6
Cm
. Искомая вероятность будет
3
1
45
15
n
m
p
.
6. В цехе работают 6 мужчин и 4 женщины. По табельным номерам
наудачу отобраны 7 человек. Найти вероятность того, что среди отобранных
лиц три женщины.
Общее число возможных исходов равно числу способов, которыми
можно отобрать 7 человек из 10, т.е.
3
10
7
10
CCn
.
Найдем число исходов, благоприятствующих интересующему нас
событию: трех женщин можно выбрать из четырех
3
4
C
способами; при этом
остальные четыре человека должны быть мужчинами, их можно отобрать
4
6
C
способами. Следовательно, число благоприятствующих исходов равно
2
6
1
4
4
6
3
4
CCCC
.
Искомая вероятность
2
1
32
8910
2
56
4
3
10
2
6
1
4
C
CC
p
.
7. Пять книг расставляются на полку. Найти вероятность того, что две
определенные книги окажутся рядом.
Число всех способов, которыми можно расставить на полке пять книг,
равно числу перестановок из пяти элементов
!5
5
5
An
.
Подсчитаем число благоприятствующих случаев. Две определенные
книги можно поставить рядом 2!=2 способами. Оставшиеся книги можно
расположить на полке
!34
способами. Поэтому
!342 m
.
Итак,
4,0
!5
!342
p
.
Относительная частота события.
Статистическая вероятность

Недостатком классического определения вероятности является то, что не
всегда удается узнать, являются исходы испытания равновозможными или не
являются.
Относительной частотой р
*
случайного события А называется отношение
числа m
*
появления данного события к общему числу n
*
проведенных
одинаковых испытаний, в каждом из которых могло появиться или не
появиться данное событие.
*
*
**
)(
n
m
pAP
.
Оказывается, что при большом числе испытаний n, относительная
частота появления события А в различных сериях отличается друг от друга
мало и это отличие тем меньше, чем больше испытаний в сериях.
При статистическом определении вероятностью события называют
относительную частоту события при большом числе испытаний или число
близкое к ней:
)(lim)(
*
*
APAP
n
.
Сложение вероятностей
Суммой двух событий А и B называется событие С, состоящее в
появлении хотя бы одного из этих событий. Сумма обозначается:
С=А+В=АилиВ.
Теорема о сложении вероятностей. Вероятность появления одного из
двух несовместных событий равна сумме вероятностей этих событий.
Р(АилиВ)=Р(А)+Р(В).
Заметим, что сформулированная теорема справедлива для любого числа
слагаемых:
n
i
i
n
i
i
APAP
11
)(
.
Два события называются противоположными, если они несовместны и
образуют полную группу. Если событие обозначим через А, то
противоположное ему – через
A
.
Так как при испытании обязательно произойдет или событие А или
событие
A
, то согласно теореме о сложении вероятностей получаем
1)()( APAP
.
Если случайные события А
1
, А
2
,…, А
n
образуют полную группу
несовместных событий, то имеет место равенство
1)(...)()(
21
n
APAPAP
.
Случайные события А и B называются совместными, если при данном
испытании могут произойти оба эти события. Событие, заключающееся в
совмещении событий А и B, будем обозначать АиВ или АВ.
Теорема. Вероятность суммы совместных событий вычисляется по
формуле

)()()()( ABPBPAPBAP
.
Примеры. 1. В урне 10 белых, 15 черных, 20 синих и 25 красных шаров.
Вынули один шар. Найти вероятность того, что вынутый шар а) синий или
черный; б) белый, черный или синий.
Обозначим следующие события:
Б – вынули белый шар,
70
10
)( БP
;
Ч – вынули черный шар,
70
15
)( ЧP
;
С – вынули синий шар,
70
20
)( CP
;
К – вынули красный шар,
70
25
)( KP
.
Тогда искомые вероятности будут:
а)
2
1
70
15
70
20
)()()( ЧPCPЧCP
.
б)
14
9
70
20
70
15
70
10
)()()()( CPЧPБPCЧБP
или
14
9
70
25
1)(1)( KPCЧБP
.
2. На стеллаже в библиотеке стоит 15 учебников, причем 5 из них в
переплете. Библиотекарь берет три учебника. Найти вероятность того, что
хотя бы один из взятых учебников окажется в переплете.
Рассмотрим два способа решения задачи.
Первый способ. Пусть события А – хотя бы один учебник в переплете;
В – один из взятых учебников в переплете, два – без переплета;
С – два в переплете, один без переплета;
D – все три учебника в переплете.
Очевидно, А=В+С+D. Найдем вероятности событий В, С, и D.
91
45
)(
3
15
2
10
1
5
C
CC
BP
,
91
20
)(
3
15
1
10
2
5
C
CC
CP
,
91
2
)(
3
15
3
5
C
C
DP
.
Тогда
91
67
)()()()( DPCPBPAP
.
Второй способ. Вновь А – хотя бы один учебник в переплете;
A
- ни один из взятых учебников не имеет переплета.
Так как события А и
A
противоположные, то
91
67
91
24
11)(1)(
3
15
3
10
C
C
APAP
.
Умножение вероятностей независимых событий
Событие А называется независимым от события В, если вероятность
появления события А не зависит от того, произошло событие В или нет.
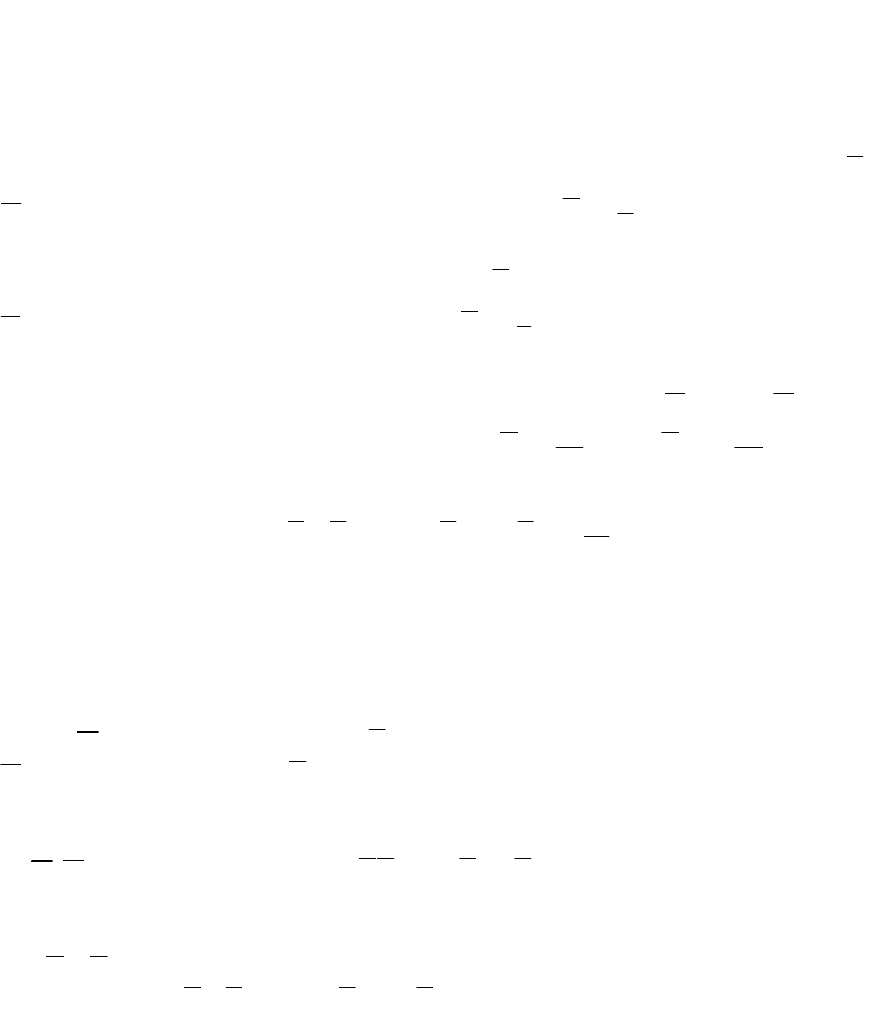
Теорема. Вероятность совместного появления двух независимых
событий равна произведению вероятностей этих событий
Р(АВ)=Р(А)·Р(В).
Заметим, что теорему о вероятности суммы совместных событий можно
записать теперь в виде:
)()()()()( BPAPBPAPBAP
.
Примеры. 1. В первом ящике 2 белых и 7 черных шаров, во втором 8
белых и 4 черных шара. Из каждого ящика вынули по шару. Найти
вероятность того, что один из вынутых шаров белый, а другой – черный.
Обозначим события: А – вынули белый шар из первого ящика,
6
1
)( AP
;
A
- вынули черный шар из первого ящика,
6
5
)( AP
;
В – белый шар из второго ящика,
3
2
)( BP
;
B
- черный шар из второго ящика,
3
1
)( BP
.
Нам нужно, чтобы произошло одно из событий
BA
или
BA
. По
теореме об умножении вероятностей
18
1
)( BAP
,
18
10
)( BAP
. Тогда
искомая вероятность по теореме сложения будет
18
11
)()()( BAPBAPBABAPP
.
2. Вероятность попадания в цель у первого стрелка 0,8, у второго – 0,9.
Стрелки делают по выстрелу. Найти вероятность: а) двойного попадания;
б) хотя бы одного попадания; г) одного попадания.
Пусть А – попадание первого стрелка, Р(А)=0,8;
В – попадание второго стрелка, Р(В)=0,9.
Тогда
A
- промах первого,
2,08,01)( AP
;
B
- промах второго,
1,09,01)( BP
.
Найдем нужные вероятности.
а) АВ – двойное попадание, Р(АВ)=Р(А)Р(В)=0,72.
б)
A
B
- двойной промах,
02,0)()()( BPAPBAP
.
в) А+В – хотя бы одно попадание,
98,072,09,08,0)()()()( ABPBPAPBAP
.
г)
BABA
- одно попадание,
26,09,02,01,08,0)()()( BAPBAPBABAP
.
3. Студент разыскивает нужную ему формулу в трех справочниках.
Вероятности того, что формула содержится в первом, втором и третьем
справочниках равны 0,6; 0,7 и 0,8 соответственно. Вычислить вероятность
того, что формула содержится 1) только в одном справочнике; 2) только в
двух справочниках; 3) во всех трех справочниках.
А – формула содержится в первом справочнике;
В – формула содержится во втором справочнике;
С – формула содержится в третьем справочнике.
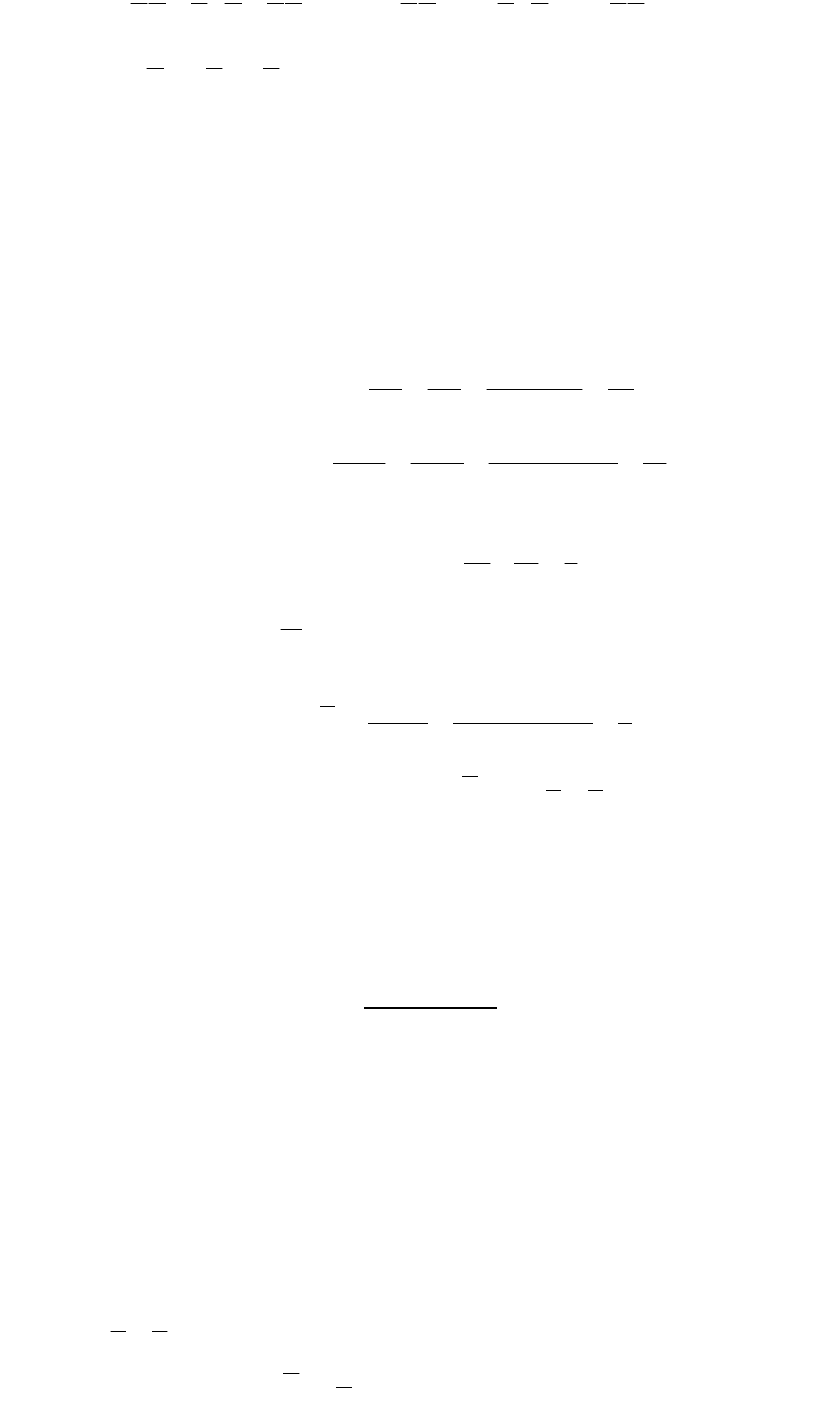
Воспользуемся теоремами сложения и умножения вероятностей.
1.
)()()()( CBAPCBAPCBAPCBACBACBAP
=0,6·0,3·0,2+0,4·0,7·0,2+0,4·0,3·0,8=0,188.
2.
452,08,07,04,08,03,06,02,07,06,0)( BCACBACABP
.
3.З(АВС)=0,6·0,7·0,8=0,336.
4. Из 10 деталей 7 – стандартные. Наудачу берут 6 деталей. Вычислить
вероятность того, что среди них: а) не более одной нестандартной; б) не
более двух нестандартных.
а) Обозначим события А – среди взятых 6 деталей нестандартных нет;
В – в 6 выбранных деталях одна нестандартная. Тогда А+В – среди 6
деталей не более одной нестандартной. Найдем Р(А+В). Заметим, что
30
1
78910
4327
)(
4
10
1
7
6
10
6
7
C
C
C
C
AP
,
10
3
789102
432673
)(
4
10
2
7
1
3
6
10
5
7
1
3
C
CC
C
CC
BP
.
Откуда
3
1
10
3
30
1
)( BAP
.
б) Пусть теперь событие А – в шести взятых деталях не более двух
нестандартных. Тогда
A
- в выбранных деталях более двух нестандартных,
т.е. три.
6
1
7891032
432567
)(
6
10
3
7
31
3
C
CC
AP
.
6
5
6
1
1)(1)( APAP
.
Зависимые события. Условная вероятность.
Формула полной вероятности
Событие А называется зависимым от события В, если вероятность
появления события А зависит от того, произошло или нет событие В.
Вероятность того, что произошло А при условии, что произошло
событие В, будем обозначать P(A/B) и называть условной вероятностью
события А при условии В.
Например. В урне находятся 3 белых шара и 2 черных. Из урны
вынимается один шар, а затем второй. Событие В – появление белого шара
при первом вынимании. Событие А – появление белого шара при втором
вынимании.
Очевидно, что вероятность события А, если событие В произошло, будет
2
1
4
2
)/( BAP
. Вероятность события А при условии, что событие В не
произошло, будет
4
3
)/( BAP
.
