Skiadas C.H., Dimotikalis I. (editors) Chaotic Systems: Theory and Applications

38

D.

Becerra Alonso and

V.

Tereshko

gRsin

(8 +

(j

-

2)~)

R2

(-vw + gR

l:i

mi

sin (8 +

i~))

(8)

d

2

,(j?3)

= fo + R

2

l:i

mi

- (fo +

R2l:i

mi)2

(9)

The

elements

d(j?3),1

would

be

different from zero in

the

unsimplified case.

4

Jacobian-based

local

Lyapunov

exponents

We

expect

the

values

of

Ii

within

the

chaotic regime

to

be

positive.

For

the

numerical

test,

we

choose

Ii

= 0.02. After

ensuring

that

the

transient

is over,

these

are

the

temporal

dynamics

of

w(t)

and

the

local

Lyapunov

exponents.

8

1220 1240 1260 1280 1300 1320 1340 1360 1380 1400

t

-2.5

'::::---:-::'::-=----:~----::'::-:---_:_::"-=--~___:-"------'.---'----.l.----.J

1200 1220 1240 1260 1280 1300 1320 1340 1360 1380 1400

t

Fig.

2.

wand

Local

Lyapunov

exponents

vs.

time

for ij = 0.02. All

other

parame-

ters

remain

as above.

Two

consequences

can

be

inferred from

this

result.

The

most

direct

is

that

the

average of

ALyapunov

is clearly negative. We will go into

detail

about

this

on

the

The

second is

that

we

can

find

an

inverse

proportionality

between an-

gular

acceleration

and

the

local

Lyapunov

exponents.

Every

time

w

hits

an

extreme

or

goes

through

an

inflexion

point,

there

is a

corresponding

peak

in

Local and Global Lyapunov Exponents

in

a Discrete Mass Waterwheel

39

the

temporal

dynamics

of

ALyapunov.

As we

can

see in

Figure

2,

the

more

significant

peaks

are

those

when

w is going

through

a low slope inflexion

point

or

an

extreme

of

w

happens

close

to

w =

o.

This

has

an

equivalent physical

explanation

when

we

think

about

the

be-

haviour

of

the

waterwheel.

Higher

local

Lyapunov

exponents

imply

a

higher

sensitive

dependence

to

initial

conditions

at

that

particular

state

of

the

sys-

tem.

Malkus'

waterwheel

was

expected

to

have

different

sensitivity

depending

on

w.

When

w is close

to

zero,

the

waterwheel

is slowing down,

and

the

sum

of

the

torques

exerted

by

the

water

on

each

one

of

the

buckets will decide

if

it

keeps

rotating

in

the

same

direction

or

not.

In

such

a

tipping

point,

very different

future

states

of

the

system

are

being

decided,

and

therefore

the

sensitivity

to

any

perturbation

is high.

One

of

the

things

that

makes

Malkus'

waterwheel

a challenging

model

is

that

predictions

beyond

any

of

these

tipping

points

are

very

difficult,

and

these

are

happening

just

a few

seconds

apart

from

each

other.

5

Reasons

for

Alocal

< 0

in

chaos

The

local

Lyapunov

exponents

calculated

in

the

were

the

result

of

obtaining

the

eigenvalues

of

the

Jacobian,

calculating

the

absolute

values, choosing

the

highest

one,

and

applying

the

natural

logarithm.

This

goes

with

the

standard

definition of

Lyapunov

exponent.

However,

the

Ja-

cobian

as a derivative

has

a

very

strong

limitation

in

this

particular

system

when

we

try

to

use

it

as a

means

to

measure

the

long

term

butterfly

effect.

Our

equations

for

the

waterwheel, as we

presented

them

in

Section

1,

are

piecewise

because

of

q(

8).

Though

the

complete

system

presents

nonlinearity

and

chaos

(with

the

right

parameters),

each one

of

the

individual

piecewise

subsystems

is convergent.

This

can

also

be

translated

into

a physical

explanation:

as

long

as

the

top

faucet keeps

on

filling

the

same

bucket

while

the

others

drain,

the

system

will

be

converging.

At

the

very

moment

when

a new

bucket

is

the

one

under

the

faucet,

the

convergent

state

of

the

system

is displaced,

and

the

system

will

start

approaching

that

new convergent

state.

It's

this

permanent

shift

of

stationary

states

that

keeps

the

waterwheel

going.

But

of

course

that

means

that

our

derivatives

are

those

of

a convergent

subsystem,

part

of

the

complete

piecewise

system.

This

makes

it

natural

for

the

corresponding

Lyapunov

exponents

to

be

negative.

Even

if

we

had

not

proposed

the

simplified

Jacobian,

the

result

would

remain

the

same,

because

the

difference would only

be

relevant

during

transitions

between

buckets,

while

the

rest

of

the

local

Lyapunov

exponents

stay

negative.

It

is

the

long

term

permanent

transition

between

buckets

that

eventually

allows

the

but-

terfly effect

to

take

over,

and

no local

and

short

term

analysis will show this.

In

Figure

3 we

can

see

the

temporal

dynamics

of

the

system

under

two

initial

conditions

separated

by

a

distance

Do =

10-

11

.

Two

stages

are

eas-

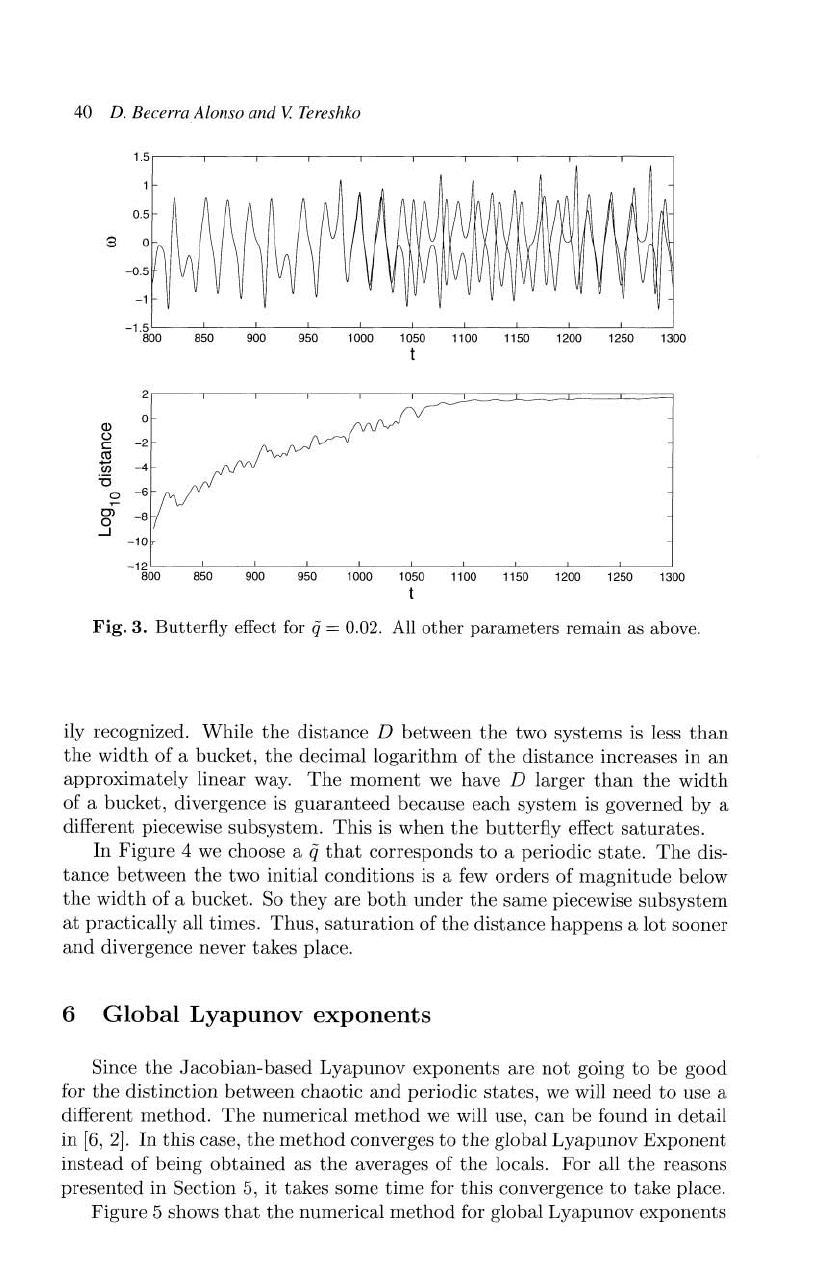
40

D.

Becerra Alonso and

V.

Tereshko

1.5~--------~--~----~--~----~----~--~----~---,

8

-1.5

800 850

900 950

1000 1050

1100 1150 1200 1250 1300

t

2

OJ

0

U

-2

C

ell

ii5

-4

'5

0

OJ

0

....J

850

900

950

1000 1050

1100

1150

1200 1250 1300

t

Fig.

3.

Butterfly

effect for q = 0.02.

All

other

parameters

remain

as

above.

ily recognized.

While

the

distance

D

between

the

two

systems

is less

than

the

width

of

a

bucket,

the

decimal

logarithm

of

the

distance

increases

in

an

approximately

linear

way.

The

moment

we

have

D

larger

than

the

width

of

a

bucket,

divergence is

guaranteed

because

each

system

is

governed

by

a

different piecewise

subsystem.

This

is

when

the

butterfly

effect

saturates.

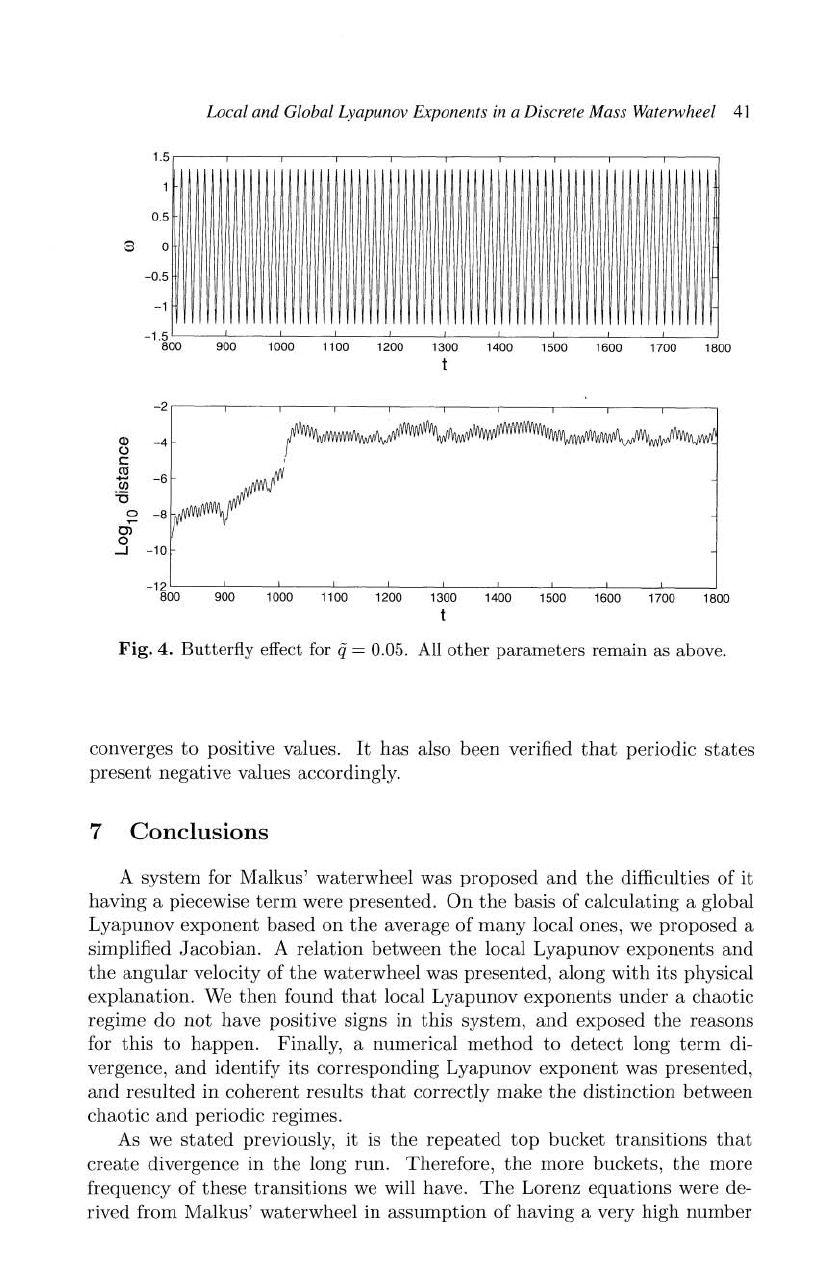
In

Figure

4 we choose a q

that

corresponds

to

a

periodic

state.

The

dis-

tance

between

the

two

initial

conditions

is a few

orders

of

magnitude

below

the

width

of

a

bucket.

So

they

are

both

under

the

same

piecewise

subsystem

at

practically

all times.

Thus,

saturation

of

the

distance

happens

a

lot

sooner

and

divergence

never

takes

place.

6

Global

Lyapunov

exponents

Since

the

Jacobian-based

Lyapunov

exponents

are

not

going

to

be

good

for

the

distinction

between

chaotic

and

periodic

states,

we will

need

to

use a

different

method.

The

numerical

method

we will use,

can

be

found

in

detail

in

[6,

2].

In

this

case,

the

method

converges

to

the

global

Lyapunov

Exponent

instead

of

being

obtained

as

the

averages

of

the

locals.

For

all

the

reasons

presented

in

Section

5,

it

takes

some

time

for

this

convergence

to

take

place.

Figure

5 shows

that

the

numerical

method

for global

Lyapunov

exponents

Local and Global Lyapunov Exponents

in

a Discrete Mass Waterwheel

41

1.5

0.5

8

0

-0.5

-1

-1.5

800

900

1000 1100

1200 1300 1400

1500 1600

1700 1800

t

-2

OJ

()

-4

C

(1j

U5

'0

0

r::il

0

-.I

-10

-12

800

900

1000

1100

1200 1300

1400

1500 1600

1700 1800

t

Fig.

4.

Butterfly

effect for

ij

= 0.05.

All

other

parameters

remain

as

above.

converges

to

positive values.

It

has

also

been

verified

that

periodic

states

present

negative

values accordingly.

7

Conclusions

A

system

for

Malkus'

waterwheel

was

proposed

and

the

difficulties

of

it

having

a piecewise

term

were

presented.

On

the

basis

of

calculating

a global

Lyapunov

exponent

based

on

the

average

of

many

local ones, we

proposed

a

simplified

Jacobian.

A

relation

between

the

local

Lyapunov

exponents

and

the

angular

velocity

of

the

waterwheel

was

presented,

along

with

its

physical

explanation.

We

then

found

that

local

Lyapunov

exponents

under

a

chaotic

regime

do

not

have

positive

signs

in

this

system,

and

exposed

the

reasons

for

this

to

happen.

Finally, a

numerical

method

to

detect

long

term

di-

vergence,

and

identify

its

corresponding

Lyapunov

exponent

was

presented,

and

resulted

in

coherent

results

that

correctly

make

the

distinction

between

chaotic

and

periodic

regimes.

As we

stated

previously,

it

is

the

repeated

top

bucket

transitions

that

create

divergence

in

the

long

run.

Therefore,

the

more

buckets,

the

more

frequency

of

these

transitions

we will have.

The

Lorenz

equations

were de-

rived from

Malkus'

waterwheel

in

assumption

of

having

a

very

high

number

42

D. Becerra

Alonso

and

V.

Tereshko

1.5

1

Mw~}~\~

1~~~\~1~W~~j~~~~~~

0.5

8

0

-0.5

-1

-1.5

1100 1200 1300

1400 1500 1600 1700 1800

0.2

0.15

>

0

c

0.1

:::J

C.

'"

>.

0.05

....I

«

-0.05

1100 1200 1300 1400

1500 1600 1700 1800

Fig.

5.

Global

Lyapunov

exponent

obtained

using

[6,

2]

where

q = 0.02.

of

buckets.

This

is

why

Lorenz

presents

immediate

divergence in its

chaotic

regime while

the

waterwheel

takes

longer.

An

extra

nonlinearity

in

the

mass

equation

could close

this

gap

between Lorenz

and

the

discrete waterwheel.

Bibliography

[1]

David

Becerra

and

Valery Tereshko.

Chaotic

waterwheel: Discrete vs

continuous

mass

representation.

Chaos2008 Proceedings, 1, 2008.

[2]

Giancarlo

Benettin,

Luigi Galgani,

and

Jean-Marie

Strelcyn. Kolmogorov

entropy

and

numerical experiments. Phys. Rev.

A,

14:2338-2345, 1976.

[3]

M. Kolr

and

G.

Gumbs.

Theory

for

the

experimental

observation

of

chaos

in

a

rotating

waterwheel. Physical Review

A,

45(2):626-637, 1992.

[4]

E.

N.

Lorenz.

Deterministic

non-periodic flows.

J.

Atmas.

Sci, 1963.

[5]

W.

V.

R.

Malkus. Non-Periodic convection

at

high

and

low

prandtl

num-

ber. Mem. Soc. R. Sci. Liege, 6(IV):125, 1972.

[6]

A. Wolf,

J.

B. Swift, H.

L.

Swinney,

and

J.

A.

Vastano.

Determining

lyapunov

exponents

from a

time

series. Physica

D,

16(3):285-317, 1985.

43

Complex

Dynamics

in

an

Asset

Pricing

Model

with

Updating

Wealth

Serena

Brianzonil,

Cristiana

Mammana

2

,

and

Elisabetta

Michetti

3

1

University

of

Macerata

Dep.

of

Economic

and

Financial

Institutions

62100

Macerata,

Italy

(e-mail:

brianzoni@unimc.i

t)

2

University

of

Macerata

Dep.

of

Economic

and

Financial

Institutions

62100

Macerata,

Italy

( e-mail: mammana@unimc.i

t)

3

University

of

Macerata

Dep.

of

Economic

and

Financial

Institutions

62100

Macerata,

Italy

(e-mail:

michetti@unimc.i

t)

Abstract:

We

consider

an

asset

pricing

model

with

wealth

dynamics

and

hetero-

geneous

agents.

By

assuming

that

all

agents

belonging

to

the

same

group

agree

to

share

their

wealth

whenever

an

agent

gets

in

the

group

(or

leaves

it),

we

develop

an

adaptive

model

which

characterizes

the

evolution

of

the

wealth

distribution

when

agents

switch

between

different

trading

strategies.

Two

groups

with

hetero-

geneous

beliefs

are

considered:

fundamentalists

and

chartists.

The

model

results

in

a

nonlinear

three-dimensional

dynamical

system,

which

is

studied

in

order

to

investigate

complicated

dynamics

and

to

explain

the

effects

on

wealth

distribution

among

agents

in

the

long

run.

Keywords:

heterogeneous

agents,

wealth

dynamics,

nonlinear

dynamical

systems.

1

Introduction

In

recent

years, seyeral

models

have

focused

on

the

study

of

the

asset

price

dynamics

and

wealth

distribution

when

the

economy is

populated

by

bound-

edly

rational

heterogeneous

agents

with

Constant

Relative

Risk A version

(CRRA)

preferencf)s.

Chiarella

and

He[2]

study

an

asset

pricing

model

with

heterogeneous

agents

and

fixed

population

fractions. In

order

to

obtain

a

more

appealing

framework,

Chiarella

and

He[3] allow

agents

to

switch

be-

tween different

trading

strategies.

More

recently,

Chiarella

et

al.[4]

consider

a

market

maker

model

of

asset

pricing

and

wealth

dynamics

with

fixed pro-

portions

of

agents. A large

part

of

contributions

to

the

development

and

analysis

of

financiE,j models

with

heterogeneous

agents

and

CRRA

utility

do

not

consider

that

agents

can

switch

between

different

predictors.

Moreover,

the

models

which allow

agents

to

switch

between

different

trading

strategies

make

the

following simplified

assumption:

when

agents

switch

from

an

old

strategy

to

a new

strategy,

they

agree

to

accept

the

average

wealth

level of

agents

using

the

new

strategy.

44

S.

Brianzoni,

C.

Mammal1{l,

and

E.

Michetti

Motivated

by

such

considerations,

we develop a

new

model

based

upon

a

more

realistic

assumption.

In fact, we

assume

that

all

agents

belonging

to

the

same

group

agree

to

share

their

wealth

whenever

an

agent

joins

the

group

(or leaves

it).

The

most

important

fact is

that

the

wealth

of

the

new

group

takes

into

account

the

wealth

realized

in

the

group

of

origin,

whenever

agents

switch

between

different

trading

strategies.

This

leads

the

final

system

to

a

particular

form,

in

which

the

average

wealth

of

agents

is defined

by

a

continuous

piecewise

function

and

the

phase

space

is

divided

into

two

regions.

Nevertheless,

our

final

dynamical

system

is

three

dimensional

and

we

can

find all

the

equilibria.

We

will

prove

that

it

admits

two

kinds

of

steady

states,

fundamental

steady

states

(with

the

price

being

at

the

fundamental

value)

and

non

fundamental

steady

states.

Several

numerical

simulations

supplement

the

analysis.

2

The

model

Consider

an

economy

composed

of

one

risky

asset

paying

a

random

dividend

Yt

at

time

t

and

one

risk

free

asset

with

constant

risk

free

rate

7'

= R - 1 >

O.

We

denote

by

Pt

the

price

(ex

dividend)

per

share

of

the

risky

asset

at

time

t. In

order

to

describe

the

wealth's

dynamics,

we

assume

that

all

agents

belonging

to

the

same

group

agree

to

share

their

wealth

whenever

an

agent

joins

the

group

(or leaves

it).

Hence,

the

dynamics

of

the

wealth

of

investor

h

is

described

by

the

following

equation:

where

Zh,t is

the

fraction

of

wealth

that

agent-type

h invests

in

the

risky

asset,

Pt

=

Pt+Yt-Pt-l

is

the

return

on

the

risky

asset

at

period

t

and

Wh

t is

Pt-l

')

the

average

wealth

of

agent

type

h

at

time

t defined as

the

total

wealth

of

group

h

in

the

fraction

of

agents

belonging

to

this

group.

The

individual

demand

function

Zh,t derives from

the

maximization

prob-

lem

of

the

expected

utility

of

Wh,t+1, i.e. Zh,t =

max

Zh

•

t

Eh,duh(Wh,Hd],

where

Eh,t

is

the

belief

of

investor-type

h

about

the

conditional

expectation,

based

on

the

available

information

set

of

past

prices

and

dividends. Following

Chiarella

and

He[2],

the

optimal

(approximated)

solution

is given by:

where

Ah

is

the

relative

risk

aversion

coefficient

and

O"~

=

Va7'h,dpt+l

-

7']

is

the

belief

of

investor

h

about

the

conditional

variance

of

excess

returns.

In

our

model, different

types

of

agents

have

different beliefs

about

future

variables

and

prediction

selection

is

based

upon

a

performance

measure

(h,t.

Let

nh,t

be

the

fraction

of

agents.

using

strategy

h

at

time

t.

Hence, as

in

Broch

and

Hommes[l],

the

adaptation

of

beliefs is given by:

Complex Dynamics

in

Asset Pricing Model with Updating

Wealth

45

Zt+1 = L exp[,B(¢h,t - C

h

)]

h

where

th

e

parameter

,B

is

the

intensity

of

choice

measuring

how fast

agents

choose

between

different

predictors

and

Ch

:::::

0

are

the

costs

for

strategy

h.

We

obs

e

rve

that

at

time

t + 1

agent

h

measures

his realized

performance

and

then

chooses

whether

to

stay

in

group

h

or

to

switch

to

another

on

e. Hence,

we

measure

the

past

performance

as

th

e

personal

wealth

coming

from

the

investment

in

the

risky

asset

with

resp

e

ct

to

the

average

wealth

Wh,t:

In

this

work, we focus

on

the

cas

e

of

a

mark

et

populated

by

two

groups

of

agents,

i.

e. h =

1,2,

and

assume

that

at

any

time

agents

can

move from

group

i

to

group

j,

with

i,j

=

1,2

and

i

=1=

j,

while

both

movem

e

nts

are

not

simultaneously

possible. We define .1nh,t+1 = nh,t+1 - nh,t

as

th

e difference

in

the

fraction

of

agents

of

type

h from

time

t

to

time

t +

1.

Notic

e

that

in

a

market

with

two

groups

of

agents

it

follows

that

.1nl,t+1

=

-.1n2,t+1.

As

a

consequ

ence, we

can

have

two different cases:

1)

.1nl,t+1

:::::

0, if

.1nl

,t+1

fraction

of

agents

moves from

group

2

to

group

1

at

tim

e t + 1,

2)

.1nl

,t

+1

< 0, if

.1nl

,

t+1

fraction

of

agents

mov

es from

group

1

to

group

2

at

time

t +

1.

Following

Brock

and

Hommes[l],

we define

th

e difference

in

fractions

at

h

-

I

+m

t d -

I-mt

·th·

time

t,

i.

e.

mt

=

nl

,t - n2,t, so t

at

nl,t

-

-2-

an

n2,t -

-2-

'

WI

.

Afterwards

,

conditions

.1nl,t+1

:::::

0

and

.1nl

,t+ 1 < 0

can

be

re

placed

by

mt+

I

:::::

mt

and

mt+1 <

mt,

respectively. _

In

order

to

describe

the

wealth

dynamics

of

each

group,

we define

Wh,t

as

the

shar

e

of

wealth

produced

by

group

h

to

the

total

wealth:

which

we call weighted average wealth

of

group h. He

nc

e,

the

weighted

average

wealth

of

group

1

at

time

t + 1 is given by:

{

.1nl,t+1

W

2

,

t+

1 +

nl,t

WI

,t+

1

WI

,

t+1

= =

nl

,t

(WI

,t+

1 - W

2

,t

+d

+

nl

,

t+1

W2

,

t+I

,

nl

,

t+1

WI

,t+

I , if

mt

+ 1 <

mt

46

S.

Brianzoni,

C.

Mammana,

and

E.

Michetti

In

a similar way we

can

derive

the

weight

ed

average wealth

of

group

2:

Finally, we define

Wh

,t as

the

weighted average wealth

of

group

h in

the

total

weighted average we

alth

, i.

e.

Wh

,t = Wh,

t/

Lh

Wh,t

wher

e Wh,t =

nh

,tWh,t

and

h =

1,2.

In

th

e following, we will consider

the

dynamics

of

the

state

variable

Wt

:=

wl,t

-

W2

,t, i.e.

the

difference in

th

e relative weighted

average wealths. As a consequence,

the

dynamics

of

th

e

state

variable

Wt

can

be described by

the

following system:

where:

{

Fl

+ 1

Wt

+1 = G

F2

-1

G

if

ffit+1

~

mt

if

mt+1 <

mt

FI

=

_21~.::n:'

:

1(I-Wt)[R+Z2

,

t(pt+1-r)],

F2

= 2 1 i::'+

1

(1

+ Wt)[R + ZI,t(Pt+1 - r)],

G =

(1

- Wt)[R +

Z2,t(Pt+1

-

r)]

+

(1

+ Wt)[R + Zl,t(PHl - r)].

In

this

work we assume

that

price

adjustments

are

operated

by a

mar-

ket

maker

who knows

the

fundamental

price, see Chiarella

et

al.[4]

. After

assuming an i.i.d. divide

nd

process

and

zero

supply

, we obtain:

Pt+l-Pt

(I+Wt

l-

W

t)

=---'-------=--

= a

ZI

t

---

+

Z2

t

---

.

Pt

'2'

2

We

analy

ze

the

case in which agents

of

type

1

are

fundamentalists

, believ-

ing

that

pric

es

return

to

th

eir

fundam

e

nt

al value, while

traders

of

type

2

are

chartists,

who do

not

tak

e

into

account

the

fundam

e

ntal

value

but

th

eir pre-

diction selection is based

upon

a simple linear

trading

rul

e.

In

other

words,

we assume

that

EI

,

t(pt

+d =

p*

and

E

2

,t(pt+d = apt

with

a >

O.

Therefore

the

demand

functions

ar

e given by:

1

Zl,t

=

A0'2

(1

+ r)(Xt - 1),

1

Z2

,t =

A0'2

[a

- 1 + r(Xt - 1)],

where

Xt

=

~

is

the

fundamental

price ratio.

p,

The

final nonlinear

dynamical

system

T is

written

in te

rms

of

the

s

tate

variables Xt,

mt

and

Wt:

mt+1

=

h(

Xt, Wt) =

tanh

{

,6

/2

[,\~2

(Xt

- a)

[2'\"'0'2

(Xt - 2 + a + 2r(Xt -

1)

+(Xt - a)Wt) + r(Xt -

1)]-

en,

Complex Dynamics in Asset Pricing Model with Updating Wealth 47

with:

F _

-4(1-

w

t){R+6

[a-Hr(xt-

1

)][

~

(Xt

-2+a+2r(xt-

1

)+(Xt

-a)w,)+r(xt-

1

)]}

1 -

(1-m,)[exp{!3[",!2

(Xt-a)[2",Qa2

(xt-2+a+2r(xt-1)+(xt-a)w,)+r(xt-1)]-C]}+1]'

p.

4(1+wt){

R+~

(l+r

)(xt-1)

[~(Xt

-2+a+2r(xt

-1

)+(Xt

-a)w')+r(xt

-1)]}

2 -

/\17

2,\q

-

(l+m,)[exp{

-!3[

",!2

(Xt-

a

)[

2>.:2

(Xt

-2+a+2r(xt-1)+(xt

-a)w,)+r(xt-1)]-C]}+1]

'

G =

2R+

>'~2

[xt-2+a+2r(xt-l)+(xt-a)Wt]·

[2>''''0"2

(Xt

- 2 + a +

2r(xt

-

1)

+(Xt - a)Wt) +

r(xt

- 1)].

3

Results

Our

model

admits

two

types

of

steady

states:

- fundamental steady states

characterized

by

x = 1, i.e.

by

the

price being

at

the

fundamental

value,

-

non

fundamental steady states for which x

=I

1.

More precisely, for a

=I

1

the

fundamental

steady

state

E f

of

the

system

is such

that

wf

= 1

and

there

exists a

non

fundamental

steady

state

Enf

such

that

wnf

=

-1,

xnf

=

l-;:-a

+

1.

Observe

that

at

the

fundamental

(non-fundamental)

equilibrium

the

total

wealth

is owned

by

fundamentalists

(chartists).

When

a = 1

the

fixed

point

Enf

becomes a

fundamental

steady

state.

More precisely, every

point

E = (1,

tanh{

- cf},

w)

is a

fundamental

equilibrium, i.e.

the

long-run

wealth

distribution

at

a

fundamental

steady

state

is given

by

any

constant

w E [-1,1].

In

other

words, a continuum

of

steady states exists:

they

are

located

in

a one-dimensional

subset

(a

straight

line) of

the

phase

space.

In

this

case

the

steady

state

wealth

distribution

which is reached in

the

long

run

by

the

system

strictly

depends

on

the

initial

condition. Summarizing,

the

following

lemma

deals

with

the

existence

of

the

steady

states:

Lemma

1.

The number

of

the steady states

of

the

system

T depends on the

parameter a:

1.

Let a

=I

1, then:

• for a < 1

+r

there exist two steady states: the fundamental equilibrium

E f =

(X

f =

1,

rn f =

tanh

{ -

c:}

, W f =

1)

and the non-fundamental equilibrium

(

l-a

{f3[

1

l+r

2]})

Enf=

--+I,tanh

-

---(I-a)

-C

,-1

r 2

'\0'2

r

Skiadas C.H., Dimotikalis I. (editors) Chaotic Systems: Theory and Applications

Подождите немного. Документ загружается.