Сидоренко Е. Методы математической обработки в психологии

Подождите немного. Документ загружается.

Eтеор

=17*0,53=9,01

Жтеор

=110,47=5,17

Зтеор

=11*0,53=5,83

Ясно, что сумма теоретических частот по строкам будет равняться сумме всех

проявлений по данной строке. Например,

Атеор

Бтеор

=13.63+15,37=29

Втеор

Гтеор

=5,17+5,83=11

Дтеор

Етеор

=7,99+9,01=17 и т.д.

При такого рода подсчетах лучше всякий раз себя проверить. Теперь мы можем

вывести общую формулу подсчета

теор

для сопоставления двух или более

эмпирических распределений:

Соответствующими строкой и столбцом будут та строка и тот столбец, на

пересечении которых находится данная ячейка таблицы. Теперь нам лучше всего

сделать развертку Табл. 4.5, представив все ячейки от А до Ж в виде первого столбца -

это будет столбец эмпирических частот. Вторым столбцом будут записаны

теоретические частоты. Далее будем действовать по

уже известному алгоритму. В

третьем столбце будет представлены разности эмпирических и теоретических частот, в

четвертом - квадраты этих разностей, а в пятом - результаты деления этих квадратов

разностей на соответствующие каждой строке теоретические частоты. Сумма в нижнем

правом углу таблицы и будет представлять собой эмпирическую величину % (Табл.

4.6).

Таблица 4.6

Расчет критерия χ2 при сопоставлении распределений невербальных и вербальных

признаков благосклонности невесты

Ячейки таблицы

частот

Эмпирическая частота

взгляда

(

)

Теоретическая

частота

(

)

эj

-f

) (f

эj

-f

)

эj

-f

)

13,63

15,37

5,17

5,83

7,99

9,01

5,17

5,83

+0,37

-0,37

-0,17

+0,17

+0,01

-0,01

-0,17

+0,17

0,14

0,03

0,02

0,00

0,03

0,02

0,01

0,00

0,01

0,00

Суммы 68 68 0 0,04

Число степеней свободы при сопоставлении двух эмпирических распределений

определяется по формуле:

-1)·(

-1)

где

- количество разрядов признака (строк в таблице эмпирических частот);

с - количество сравниваемых распределений (столбцов в таблице

эмпирических частот).

В данном случае таблицей эмпирических частот является левая, эмпирическая

часть таблицы 4.5, а не на ее развертка (Табл. 4.6). Количество разрядов - это

количество женихов, поэтому

k=4.

Количество сопоставляемых распределений с=2.

Итак, для данного случая,

v=(4-l)(2-t)=3

Определяем по Табл. IX Приложения 1 критические значения для ν=З:

Ответ: Н

принимается. Распределения невербально и вербально выражаемых

невестой предпочтений не различаются между собой.

Итак, Агафья Тихоновна весьма последовательна в проявлении своих

предпочтений, хотя, по-видимому, сама этого пока не замечает.

Иллюстрация 2

Третий вариант развития шутливого примера: сопоставление встречных

выборов

К сожалению, в этом пункте мы от комедии вынуждены перейти к драме -

истинной драме любви. Ибо, судя по тексту пьесы, проявляемые женихами признаки

влюбленности и симпатии по отношению к невесте отнюдь не соответствуют ее

собственной системе предпочтений. У Ивана Павловича, а, главное,

у Никанора

Ивановича, которому невестой отдается столь явное предпочтение, проскальзывают в

разговоре по большей части как раз отрицательные и задумчиво-неодобрительные

отзывы о невесте: "Нос велик... Нет, не то, не то... Я даже думаю, что вряд ли она

знакома с обхождением высшего общества. Да и знает ли она еще по-французски

Благосклонных отзывов ("А сказать правду - мне понравилась она потому, что

полная женщина" и т. п.) поступило:

от Никанора Ивановича - ни одного;

от Ивана Кузьмича - 15*

от Ивана Павловича - 6*

от Балтазара Балтазарыча - 18.

Попробуем ответить на вопрос: согласуются ли распределения (благосклонных

отзывов невесты о женихах и женихов о невесте?

Мы видим, что это действительно особая задача. Мы сопоставляем два

эмпирических распределения с совпадающей классификацией разрядов, но в одном

случае это распределение реакций одного человека на четверых других, а в другом

случае это реакции четырех

человек на одного и того же человека.

Такая модель взаимных реакций может использоваться отнюдь не только в

области брачных консультаций, но и в решении задач "построения команды",

выбора заместителя, подбора пар в тех видах деятельности, где требуется активное

постоянное взаимодействие, в исследованиях социальной перцепции и взаимного

влияния, в тренинге сенситивности

и др.

Сформулируем гипотезы.

: Распределение положительных отзывов невесты совпадает с распределением

положительных отзывов женихов.

: Распределение положительных отзывов невесты не совпадает с

распределением положительных отзывов женихов.

Построим таблицу для подсчета теоретических частот.

Таблица 4.7

Эмпирические и теоретические частоты положительных высказываний невесты о

женихах и женихов о невесте

Эмпи

ические частоты Суммы Тео

етические частоты

Разряды-

женихи

Положительных

высказываний

невесты о

женихах

Положительных

высказываний

женихов о

невесте

Положительных

высказываний

невесты о

женихах

Положительных

высказываний

женихов о

невесте

Ник. Ив.

Ив. Куз.

Ив. Пав.

Бал. Бал.

15 А

6 В

9 Д

6 Ж

0 Б

15 Г

6 Е

18 З

7,20 А

10,08 В

7,20 Д

11,52 Ж

7,80 Б

10,92 Г

7,80 Е

12,48 З

Суммы

36 39 75 36 39

Теоретические частоты рассчитываем по уже известной формуле:

А теор

=15*36/75=7,20

Б теор

=15*39/75=7,80

В теор

=21*36/75=10,08

Г теор

=21*39/75=10,92

Д теор

=15*36/75=7,20

теор

=15*39/75=7,80

теор

=24*36/75=11,52

теор

=24*39/75=12,48

Суммы теоретических частот по строкам совпадают. Все дальнейшие расчеты

выполним в таблице по алгоритму.

Таблица 4.8

Расчет критерия χ2 при сопоставлении распределений высказываний невесты о женихах

и женихов о невесте

чейки

таблицы

частот

Эмпирическая

частота взгляда (f

эj

)

Теоретическая

частота (f

)

эj

-f

) (f

эj

-f

)

эj

-f

)

/ f

1 А 15 7,20 +7,80 60,84 8,45

7,80

10,08

10,92

7,20

7,80

11,52

12,48

-7,80

-4,08

+4,08

+1,80

-1,80

-5,52

+5,52

60,84

16,65

3,24

30,47

7,80

1,65

1,52

0,45

0,42

2,64

2,44

ммы 75 75 0 25,37

Определим число степеней свободы V по количеству строк k и столбцов с в

левой части Табл. 4.7: (k=4, c=2).

v=(k-1)(c-1)

Критические значения χ2 для ν=3 нам уже известны:

Ответ: Н

отвергается. Принимается H

. Распределение положительных отзывов

предпочтений невесты не совпадает с распределением положительных отзывов

женихов (ρ<0,01).

Итак, если бы Иван Кузьмич Подколесин не сбежал, Агафью Тихоновну могло

бы ожидать не меньшее разочарование: предпочитаем

ЫЙ ею Никанор Иванович,

"тонкого поведения человек", ее отвергает.

Мы не рассмотрели лишь третью группу возможных гипотез в методе χ2. Они,

как мы помним, касаются сопоставлений одновременно 3 и более распределений.

Принцип расчетов там такой же, как и при сопоставлении двух эмпирических

распределений. Это касается и формулы расчета теоретических частот, и алгоритма

последующих расчетов.

Рассмотрим особые случаи в применении метода χ2 .

Особые случаи в применении критерия

1. В случае, если число степеней свободы ν=l, т. е. если признак принимает

всего 2 значения, необходимо вносить поправку на непрерывность

2. Если признак варьирует в широком диапазоне (например, от 10 до

140 сек. и т.п.), возникает необходимость укрупнять разряды.

Особый случай 1: поправка на непрерывность для признаков, которые

принимают всего 2 значения

Поправка на непрерывность вносится при следующих условиях: а) когда

эмпирическое распределение сопоставляется с равномерным распределением, и

количество разрядов признака k=2, a ν=k—1=1;

б) когда сопоставляются два эмпирических распределения, и количество разрядов

признака равно 2, т.е. и количество строк k=2, и количество столбцов с=2, и ν=(k—

l)*(c—1)=1.

Вариант "а": поправка на непрерывность

при сопоставлении эмпирического

распределения с равномерным. Это тот случай сопоставлений, когда мы, говоря

простым языком, проверяем, поровну ли распределились частоты между двумя

значениями признака.

Пример с поправкой на непрерывность.

В исследовании порогов социального атома

профессиональных психологов

просили определить, с какой частотой встречаются в их записной книжке мужские и

Поправка на непрерывность при ν=l предназначена для корректировки несоответствия между дискретным

биномиальным распределением и непрерывным рас пределением (Рунион Р., 1982, с. 39.)

Социальный атом "... состоит из всех отношений между человеком и окружающими его людьми, которые в

данный момент тем или иным образом с ним связаны" (Moreno J. L., 1951.)

женские имена коллег-психологов. Попытаемся определить, отличается ли

распределение, полученное по записной книжке женщины-психолога X, от равномерного

распределения. Эмпирические частоты представлены в Табл. 4.9

Таблица 4.9

Эмпирические частоты встречаемости имен мужчин и женщин в записной книжке

психолога X

Сформулируем гипотезы.

: Распределение мужских и женских имён в записной книжке X не

отличается от равномерного распределения.

: Распределение мужских и женских имен в записной книжке X отличается

от равномерного распределения.

Количество наблюдений n=67; количество значений признака k=2. Рассчитаем

теоретическую частоту:

Число степеней свободы ν=k -1=1.

Далее все расчеты производим по известному алгоритму, но с одним

добавлением: перед возведением в квадрат разности частот мы должны уменьшить

абсолютную величину этой разности

на 0,5 (см. Табл. 4.10, четвертый столбец).

Таблица 4.10

Расчет критерия % при сопоставлении эмпирического распределения имен с

теоретическим равномерным распределением

Разряды

–

принадлежность

к тому или

ином

пол

Эмпирическая

частота взгляда

эj

)

Теоретическая

частота (f

)

эj

-f

) (f

эj

-f

0,5)

эj

-f

-0,5)

эj

-f

-0,5)

Мужчины

Женщины

33,5

-11,5

+11,5

121

3,61

ммы 67 67 0 7,22

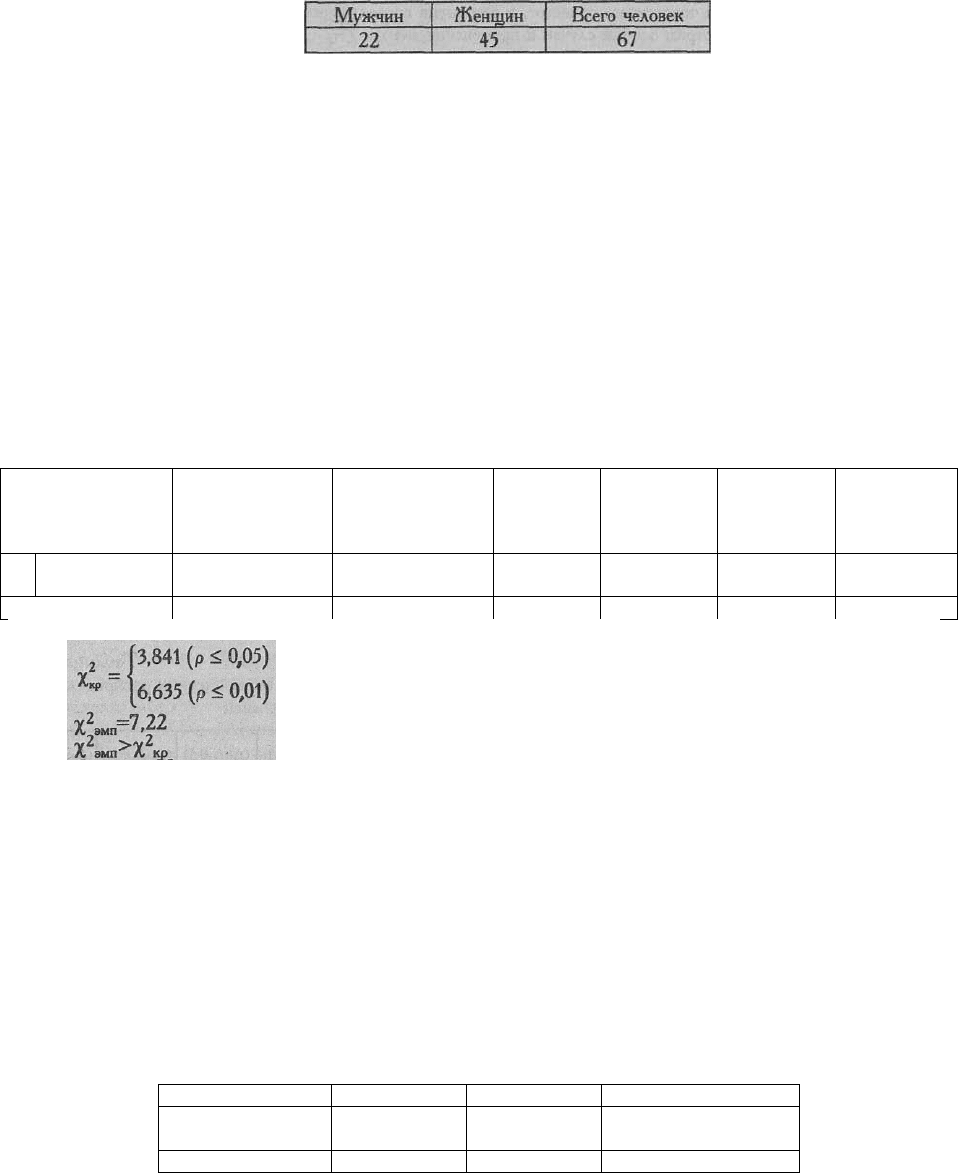
Для ν=l определяем по Табл. IX Приложения 1 критические значения:

Ответ: Н

отклоняется, принимается Н

. Распределение мужских и женских

имен в записной книжке психолога X отличается от равномерного распределения

(р<0,01).

Вариант "б": поправка на непрерывность при сопоставлении двух эмпирических

распределений

Попытаемся определить, различаются ли распределения мужских и женских имен

у психолога X и психолога С, тоже женщины. Эмпирические частоты приведены в

Табл. 4.11.

Таблица 4.11

Эмпирические частоты встречаемости

имен мужчин и женщин в записных

книжках психолога X. и психолога С.

жчин Женщин Всего человек

Психолог Х.

Психолог С.

22 А

59 В

45 Б

109 Г

168

ммы 81 154 235

Сформулируем гипотезы. H

: Распределения мужских и женских имен в двух

записных книжках

не различаются.

: Распределения мужских и женских имен в двух записных книжках

различаются между собой. Теоретические частоты рассчитываем по уже известной

формуле:

)(

)(*)(

наблюденийколичествоОбщее

столбцущемусоотвпочастотСуммастрокещейсоотвпочастотСумма

теор

−

А именно, для разных ячеек таблицы эмпирических частот,

ТЕОР

=67*81/235=23,09

Б ТЕОР

=67*154/235=43.91

В теор

=168*81/235=57,91

Г теор

=168*154/235=110,09

Число степеней свободы ν=(k—1)*(с—1)=1 Все дальнейшие расчеты проводим по

алгоритму (Табл. 4.12)

Таблица 4.12

Расчет критерия при сопоставлении двух эмпирических распределений мужских и

женских имен

чейки таблицы

эмпирических

частот

Эмпирическая

частота взгляда (f

эj

)

Теоретическая

частота (f

)

эj

-f

) (f

эj

-f

-0,5) (f

эj

-f

-0,5)

эj

-f

-0,5)

/ f

109

23,09

43,91

57,91

110,09

-1,09

+1,09

-1,09

0,59

0,35

0,015

0,008

0,006

0,003

ммы 235 235,00 0 0,032

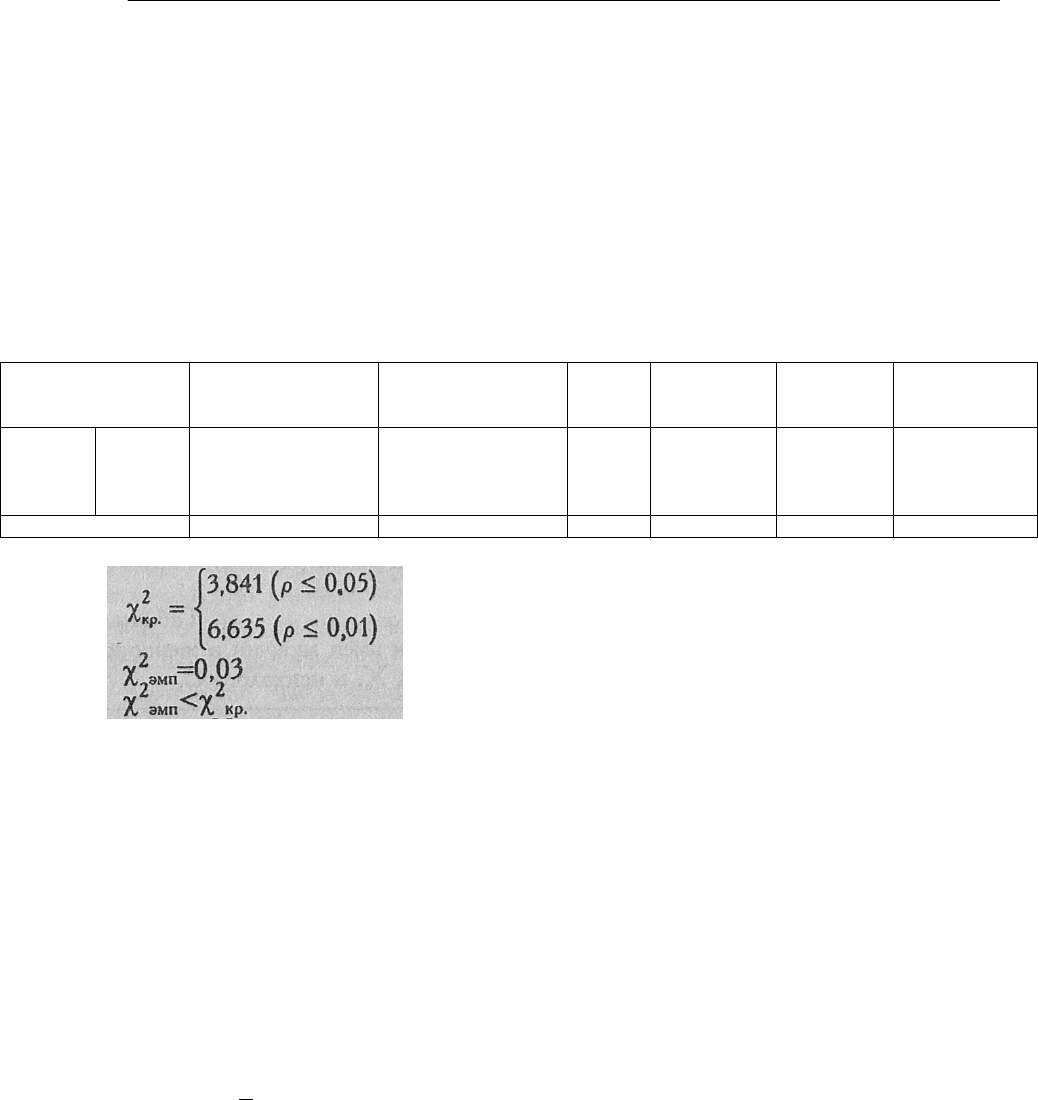
Критические значения χ2 при ν=l нам известны по предыдущему примеру:

Ответ: Н

принимается. Распределения мужских и женских имен в записных

книжка двух психологов совпадают.

Поправки на непрерывность и всех остальных подсчетов можно избежать, если

использовать по отношению к подобного рода задачам метод φ* Фишера (см.

параграф 5.4).

Особый случай 2: укрупнение разрядов признака, который варьирует в

широком диапазоне значений

Если признак варьирует в широком диапазоне значений, например, от 10 до 140

сек или от 0 до 100 мм и т. п., то вряд ли мы сможем принимать каждое значение

признака за самостоятельный разряд:

10 сек, И сек, 12 сек и т. д. до 100 сек. Одно из ограничений критерия χ

состоит в том, что теоретически на каждый разряд должно приходиться не менее 5

наблюдений: f

теор

>5. Если у признака 90 значений, и каждое из них принимается за

самостоятельный разряд, то необходимо иметь не менее 5*90=450 наблюдений! Если

же наблюдений меньше 450, то придется укрупнять разряды до тех пор, пока на

каждый разряд не будет приходиться по 5 наблюдений. Это не означает, что в ка-ждом

разряде реально должно быть 5 наблюдений;

это означает, что теоретически на каждый

разряд их приходится по 5. Рассмотрим это на примере.

Пример с укрупнением разрядов признака

Тест Мюнстерберга для измерения избирательности перцептивного внимания в

адаптированном варианте М.Д. Дворяшиной (1976) предъявлялся студентам факультета

психологии Ленинградского университета (n

=156) и артистам балета Мариинского

театра (n

=85). Материал методики состоит из бланка с набором букв русского алфавита,

в случайном порядке перемежающихся. Среди этого фона скрыто 24 слова разной

степени сложности: "факт", "хоккей", "любовь", "конкурс", "психиатрия" и т.п. Задача

испытуемого возможно быстрее отыскать их и подчеркнуть (Дворяшина М.Д., 1976, с.

124). Совпадают ли распределения количества ошибок (пропусков слов) в

двух

выборках (Табл. 4.13)?

Таблица 4.13

Эмпирические частоты пропуска слов в тесте Мюнстерберга в двух выборках

испытуемых (по данным М.Д. Дворяшиной, Е.В. Сидоренко, 1973)

разряды Эмпирические частоты пропуска слов

В группе студентов

=156)

В группе артистов

балета (n

=85)

Суммы

I. 0 пропусков

II. 1 пропуск

III. 2 пропуска

IV. 3 пропуска

V. 4 пропуска

VI. 5 пропусков

VII. 6 пропусков

VIII. 7 пропусков

IX. 8 пропусков

X. 9 пропусков

115

Суммы 156 85 241

Сформулируем гипотезы.

: Распределения ошибок (пропусков слов) в выборках студентов и артистов

балета не различаются между собой.

: Распределения ошибок (пропусков слов) в выборках студентов и артистов

балета различаются между собой.

Прежде чем перейти к расчету теоретических частот, обратим внимание на

последние 4 значения признака, от 6 пропусков и ниже. Очевидно, что f

теор

для любой

из ячеек последних 4 строк таблицы будет меньше 5. Например, для ячейки,

отмеченной кружком:

)(

)(*)(

наблюденийколичествоОбщее

столбцуемусоотвпочастотСуммастрокеейсоотвпочастотСумма

теор

−

теор

=5*85/241=1,763

Полученная теоретическая частота меньше 5.

Для того, чтобы решить, какие разряды нам следует укрупнить, чтобы f

теор

была не

меньше 5, выведем формулу расчета минимальной суммы частот по строке по формуле:

nнаименьшимсстолбцупочастотсумма

наблюденийколичествообщееf

строкепосуммаяМинимальна

яминимальнатеор

)(*

В данном случае столбцом с наименьшим количеством наблюдений является

столбец, относящийся к выборке артистов балета (n=85). Определим минимальную

сумму частот для каждой строки: Минимальная сумма по строке =5*241/85=14,16 Мы

видим, что для получения такой суммы нам недостаточно объединения последних

4 строк Табл. 4.13, так как сумма частот по ним меньше 14 (5+3+2+1=11), а

нам

необходима сумма частот, превышающая 14. Следовательно, придется объединять в

один разряд пять нижних строк Табл. 4.13: теперь любое количество пропусков от 5

до 9 будет составлять один разряд.

Однако это еще не все. Мы видим, далее, что в строке "4 пропуска" сумма

составляет всего 8. Значит, ее необходимо объединить со следующей строкой. Теперь и

3, и 4 пропуска

будут входить в один разряд. Все остальные суммы по строкам больше

14, поэтому мы не нуждаемся в дальнейшем укрупнении разрядов.

Эмпирические частоты по укрупненным разрядам представлены в Табл. 4.14.

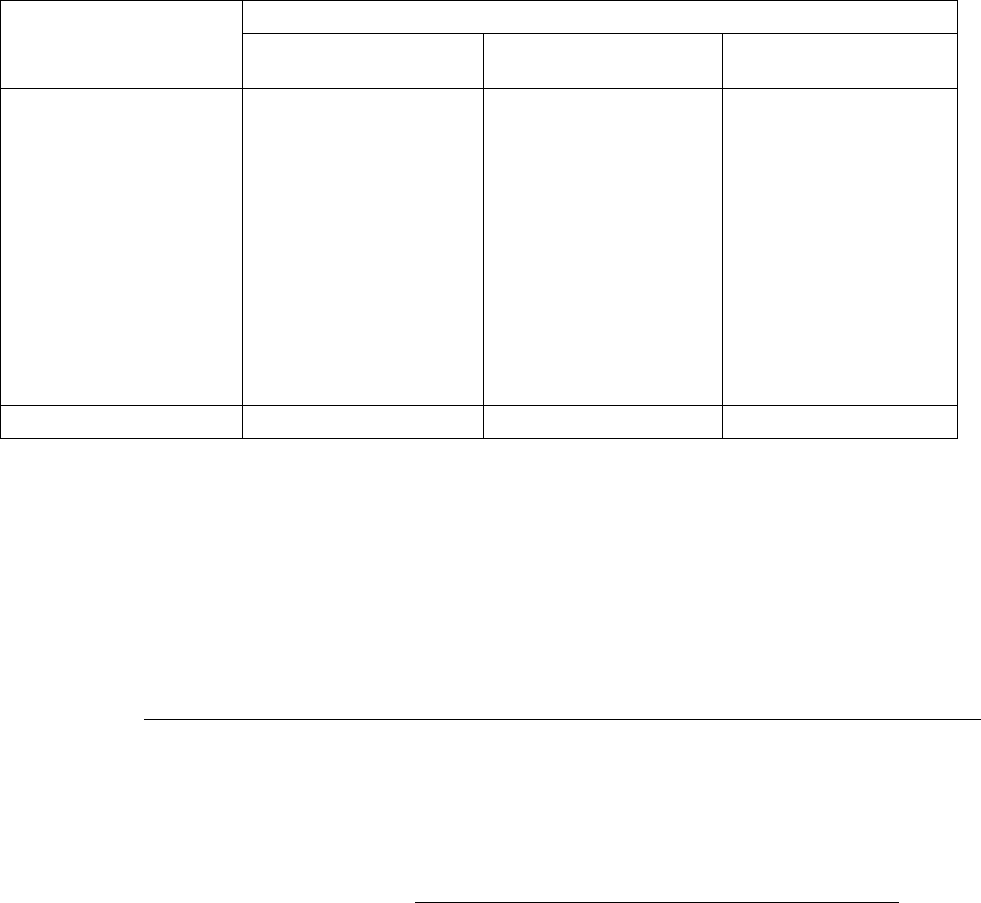
Таблица 4.14

Эмпирические частоты пропуска слов по укрупненным разрядам в двух выборках

испытуемых

Разряды Эмпи

ические частоты п

оп

ска слов

В группе студентов

(

=156

)

В группе артистов балета

(

=85

)

Суммы

I. 0 пропусков

II. 1 пропуск

III. 2 пропуска

IV. 3-4 пропуска

V. 5-9 п

оп

сков

115

ммы 156 85 241

Исследователю бывает огорчительно терять информацию, заведомо утрачиваемую

при укрупнении разрядов. Например, в данном случае нас может интересовать, удалось

ли сохранить специфический для второй выборки спад частот на 3 и 4 пропусках и

резкий их подъем на 5 пропусках (Рис. 4.7).

Сравним графики на Рис. 4.7 и Рис. 4.8. Мы видим, что спад частот во второй

выборке на

3-х и 4-х пропусках сохранился, а спад на 2-х пропусках в первой выборке

стал еще более заметным. В то же время все возможные различия в частотах в

диапазоне от 5-и до 9-и пропусков теперь оцениваются только глобально, по

соотношению общих сумм частот в этих диапазонах. По графику на Рис. 4.8 мы

уже

не можем определить, какое максимальное количество пропусков встречается в первой

группе и какое - во второй. Сопоставление распределений на этом конце становится

более грубым.

Если бы у нас было больше испытуемых в выборке артистов балета, то, возможно,

удалось бы сохранить подъем частоты на 5-и пропусках. Сейчас же нам придется

довольствоваться сопоставлением по данным укрупненным разрядам.

Перейдем к подсчету теоретических частот для каждой ячейки Табл. 4.14

А теор

=115*156/241=74,44

Б теор

=115*85/241=40,56

В теор

=47*156/241=30,41

Г теор

=47*85/241=16,59

Д теор

=27*156/241=17,47

Е теор

=27*85/241=9,53 f

Ж теор

=27*156/241=17,47

З теор

=27*85/241=9,53 f

И теор

=25*156/241=16,18 f

К теор

=25*85/241=8,82

Определим количество степеней свободы V по формуле: ν=(k -l)*(c- l) где k -

количество строк (разрядов),

с - количество столбцов (выборок). Для данного случая: ν=(5-l)*(2-l)=4

Все дальнейшие расчеты произведем в таблице по Алгоритму 13. Поправка на

непрерывность не требуется, так как v>l.

Таблица 4.15

Расчет критерия χ2 при сопоставлении двух эмпирических распределений пропусков

слов в тесте Мюнстерберга (

=156, n

=85)

Ячейки

таблицы частот

Эмпирическая

частота взгляда (f

эj

)

Теоретическая

частота (f

)

эj

-f

) (f

эj

-f

)

эj

-f

)

/ f

74,44

46,56

30,41

16,59

17,47

9,53

17,47

9,53

16,18

8,82

18,56

-18,56

-3,41

3,41

-6,47

6,47

2,53

-2,53

-11,18

11,18

344,47

11,63

41,86

6,401

124,99

4,63

8,49

0,38

0,70

2,40

4,40

0,37

0,67

7,72

14,17

Суммы 241 241 0,00 43,95

По Табл. IX Приложения 1 определяем критические значения при ν =4:

Ответ: Н

отвергается. Принимается Н

. Распределения про-пусков слов в

выборках студентов и артистов балета различаются между собой (р<0,01).

В распределении ошибок у артистов балета можно заметить два выраженных

максимума (0 пропусков и 5 пропусков), что может указывать на два возможных

источника ошибок

4.3. λ - критерий Колмогорова-Смирнова

Назначение критерия

Критерий X предназначен для сопоставления двух распределений:

а) эмпирического с теоретическим, например, равномерным или

нормальным;

б) одного эмпирического распределения с другими эмпирическим

распределением.

Критерий позволяет найти точку, в которой сумма накопленных расхождений между

двумя распределениями является наибольшей, и оценить достоверность этого

расхождения.

Описание критерия

Если в методе χ2 мы сопоставляли частоты двух распределений отдельно по

каждому разряду, то здесь мы сопоставляем сначала частоты по первому разряду, потом

по сумме первого и второго разрядов, потом по сумме первого, второго и третьего

разрядов и т. д. Таким образом, мы сопоставляем всякий раз накопленные к данному

разряду

частоты.

Если различия между двумя распределениями существенны, то в какой-то момент

разность накопленных частот достигнет критического значения, и мы сможем признать

различия статистически достоверными. В формулу критерия λ включается эта разность.

Чем больше эмпирическое значение λ, тем более существенны различия.

Гипотезы

: Различия между двумя распределениями недостоверны (судя по точке

максимального накопленного расхождения между ними).

: Различия между двумя распределениями достоверны (судя по точке

максимального накопленного расхождения между ними).

Графическое представление критерия

Рассмотрим для иллюстрации распределение желтого (№4) цвета в 8-цветном тесте

М. Люшера. Если бы испытуемые случайным образом выбирали цвета, то желтый цвет,

так же, как и все остальные, равновероятно мог бы занимать любую из 8-и позиций

выбора. На практике, однако, большинство испытуемых помещают этот цвет, "цвет

ожидания и надежды" на

одну из первых позиций ряда.

На Рис. 4.9 столбиками представлены относительные частоты

попадания желтого

цвета сначала на 1-ю позицию (первый левый столбик), затем на 1-ю и 2-ю позицию

(второй столбик), затем на 1-ю, 2-ю и 3-ю позиции и т. д. Мы видим, что высота столбиков

постоянно возрастает, так как они отражают относительные частоты, накопленные к

данной позиции. Например, столбик на 3-й позиции

имеет высоту 0,51. Это означает, что

Целесообразно было бы проверить совпадение распределения ошибок в обеих выборках с распределением

Пуассона. Закону Пуассона подчиняются распределения редких событий, приходящихся 0, 1, 2,... раз на сотни и

тысячи наблюдений. Однако в данном случае эта модель неприменима: средняя и дисперсия не равны друг другу и

составляют, соответственно, 0,91 и 1,96 в первой выборке и 2,29 и 5,43 во

второй выборке.

Относительная частота, или частость, - это частота, отнесенная к общему количеству наблюдений; в данном

случае это частота попадания желтого цвета на дан-позицию, отнесенная к количеству испытуемых. Например,

частота попадания желтого цвета на 1-ю позицию f=24; количество испытуемых n=102; относительная а f*=f

/n=0,235.