Сидоренко Е. Методы математической обработки в психологии

Подождите немного. Документ загружается.

решают быстро, поэтому большая часть значений группируется слева. В то же время

сама простота задачи может привести к тому, что некоторые испытуемые будут думать

над нею очень, очень долго, дольше даже, чем над сложной. Трудную задачу

большинство испытуемых решают в тенденции дольше, чем простую, но в то же время

почти всегда

находятся люди, которые решают ее мгновенно.

Если мы докажем, что распределения статистически достоверно различаются, это

может стать основой для построения классификаций задач и типологий испытуемых.

Например, мы можем выявлять испытуемых со стандартным соотношением признаков:

простую задачу они решают быстро, а трудную - медленно, — и испытуемых с

нестандартным соотношением: простую задачу решают

медленно, а трудную - быстро

и т.п. Далее мы можем сравнить выявленные группы испытуемых по показателям

мотивации достижения, так как известно, что лица с преобладанием стремления к успеху

предпочитают задачи средней трудности, где вероятность успеха примерно 0.5, а лица с

преобладанием стремления избегать неудачи предпочитают либо очень легкие, либо,

наоборот, очень трудные

задачи (МсСlelland D.С, Winter D.G., 1969). Таким

образом, и здесь сопоставление форм распределения может дать начало научному

поиску.

Часто нам бывает полезно также сопоставить полученное эмпирическое

распределение с теоретическим распределением. Например, для того, чтобы доказать,

что оно подчиняется или, наоборот, не подчиняется нормальному закону

распределения. Это лучше делать с помощью машинных программ обработки

данных,

особенно при больших объемах выборок. Подробные программы машинной обработки

можно найти, например, в руководстве Э.В. Ивантер и А.В. Коросова (1992).

В практических целях эмпирические распределения должны проверяться на

"нормальность" в тех случаях, когда мы намерены использовать параметрические

методы и критерии. В данном руководстве это относится лишь к методам

дисперсионного анализа, поэтому способы проверки совпадения эмпирического

распределения с нормальным описаны в Главе 7, посвященной однофакторному

дисперсионному анализу.

Традиционные для отечественной математической статистики критерии

определения расхождения или согласия распределений - это метод χ

К. Пирсона и

критерий X Колмогорова-Смирнова.

Оба эти метода требуют тщательной группировки данных и довольно сложных

вычислений. Кроме того, возможности этих критериев в полной мере проявляются на

больших выборках (n>

30). Тем не менее они могут оказаться столь незаменимыми, что

исследователю придется пренебречь экономией времени и усилий. Например, они

незаменимы в следующих двух случаях:

в задачах, требующих доказательства неслучайности предпочтений в выборе из

нескольких альтернатив;

в задачах, требующих обнаружения точки максимального расхождения между

двумя распределениями, которая затем используется для перегруппировки данных

целью применения критерия φ* (углового преобразования Фишера).

Рассмотрим вначале традиционные методы определения расхождения

распределений, а затем возможности использования критерия φ* Фишера.

4,2. χ

критерий Пирсона

Назначения критерия

Критерий χ

применяется в двух целях;

1) для сопоставления эмпирического распределения признака с теоретическим -

равномерным, нормальным или каким-то иным;

2) для сопоставления двух, трех или более эмпирических распределений одного и

того же признака

Описание критерия

Критерий χ

отвечает на вопрос о том, с одинаковой ли частотой встречаются разные

значения признака в эмпирическом и теоретическом распределениях или в двух и более

эмпирических распределениях.

Преимущество метода состоит в том, что он позволяет сопоставлять распределения

признаков, представленных в любой шкале, начиная от шкалы наименований (см. п. 1.2).

В самом простом случае

альтернативного распределения "да - нет", "допустил брак - не

допустил брака", "решил задачу - не решил задачу" и т. п. мы уже можем применить

критерий χ

Допустим, некий наблюдатель фиксирует количество пешеходов, выбравших

правую или левую из двух симметричных дорожек на пути из точки А в точку Б (см. Рис.

4.3).

Допустим, в результате 70 наблюдений установлено, что Э\ человек выбрали правую

дорожку, и лишь 19 - левую. С помощью критерия χ

мы можем определить, отличается

ли данное распределение выборов от равномерного распределения, при котором обе

дорожки выбирались бы с одинаковой частотой. Это вариант сопоставления полученного

эмпирического распределения с теоретическим. Такая задача может стоять, например,

в прикладных психологических исследованиях, связанных с проектированием в

архитектуре, системах сообщения и др.

Но представим себе, что

наблюдатель решает совершенно другую задачу: он занят

проблемами билатерального регулирования. Совпадение полученного распределения с

равномерным его интересует гораздо в меньшей степени, чем совпадение или

несовпадение его данных с данными других исследователей. Ему известно, что люди с

преобладанием правой ноги склонны делать круг против часовой стрелки, а люди с

преобладанием левой ноги

- круг по ходу часовой стрелки, и что в исследовании коллег

преобладание левой ноги было обнаружено у 26 человек из 100 обследованных.

С помощью метода χ

он может сопоставить два эмпирических распределения:

соотношение 51:19 в собственной выборке и соотношение 74:26 в выборке других

исследователей.

Это вариант сопоставления двух эмпирических распределений по простейшему

альтернативному признаку (конечно, простейшему с математической точки зрения, а

отнюдь не психологической).

Аналогичным образом мы можем сопоставлять распределения выборов из трех и

более альтернатив. Например, если

в выборке из 50 человек 30 выбрали ответ (а), 15

человек - ответ (б) и 5 человек -ответ (в), то мы можем с помощью метода χ

проверить, отличается ли это распределение от равномерного распределения или от

распределения ответов в другой выборке, где ответ (а) выбрали 10 человек, ответ (б) -

25 человек, ответ (в) - 15 человек.

В тех случаях, если признак измеряется количественно, скажем,

в баллах, секундах

или миллиметрах, нам, быть может, придется объединить все обилие значений

признака в несколько разрядов. Например, если время решения задачи варьирует от

10 до 300 секунд, то мы можем ввести 10 или 5 разрядов, в зависимости от объема

выборки. Например, это будут разряды: 0-50 секунд; 51-100 секунд; 101-150 секунд, и

т. д. Затем мы с помощью

метода χ

будет сопоставлять частоты встречаемости разных

разрядов признака, но в остальном принципиальная схема не меняется.

При сопоставлении эмпирического распределения с теоретическим мы определяем

степень расхождения между эмпирическими и теоретическими частотами.

На самом деле области применения критерия %

многообразны (см., например: Суходольский Г.В., 1972, с. 295), но в

данном руководстве мы ограничиваемся только этими двумя, наиболее часто встречающимися на практике, целями.

Доброхотова Т. А., Брагина Н. Н. Левши. М.: "Книга", 1994.

При сопоставлении двух эмпирических распределений мы определяем степень

расхождения между эмпирическими частотами и теоретическими частотами, которые

наблюдались бы в случае совпадения двух этих эмпирических распределений. Формулы

расчета теоретических частот будут специально даны для каждого варианта

сопоставлений.

Чем больше расхождение между двумя сопоставляемыми распределениями, тем

больше эмпирическое значение у}.

Гипотезы

Возможны несколько вариантов гипотез, в зависимости от задач,

которые мы перед собой ставим.

Первый вариант:

: Полученное эмпирическое распределение признака не отличается от

теоретического (например, равномерного) распределения.

: Полученное эмпирическое распределение признака отличается от

теоретического распределения.

Второй вариант:

: Эмпирическое распределение 1 не отличается от эмпирического

распределения 2.

: Эмпирическое распределение 1 отличается от эмпирического рас-

пределения 2.

Третий вариант:

: Эмпирические распределения 1, 2, 3, ... не различаются между собой.

: Эмпирические распределения 1, 2, 3, ... различаются между собой.

Критерий χ

позволяет проверить все три варианта гипотез.

Графическое представление критерия

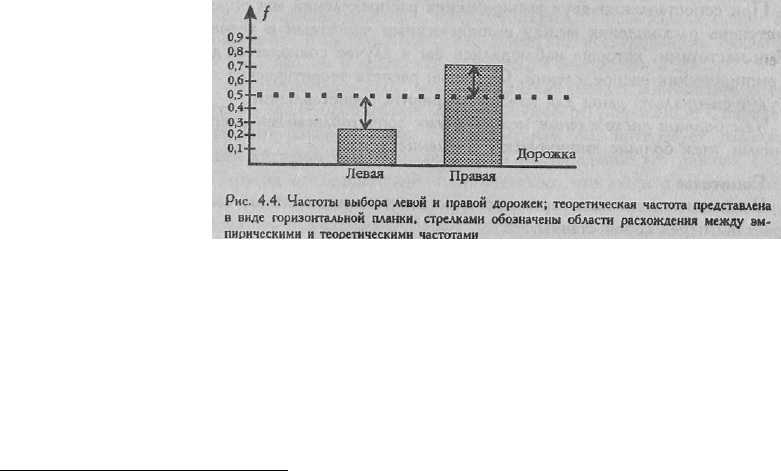
Проиллюстрируем пример с выбором правой или левой дорожек на пути из

точки А в точку Б. На Рис. 4.4 частота выбора левой дорожки представлена левым

столбиком, а частота выбора правой дорожки - правым столбиком гистограммы

. На

оси ординат отмеряются относительные частоты выбора, то есть частоты выбора той или

иной дорожки, отнесенные к общему количеству наблюдений. Для левой дорожки

относительная частота, которая называется также частостью, составляет 19/70, то есть

0,27, а для правой дорожки 51/70, то есть 0,73.

Если бы обе дорожки выбирались равновероятно, то половина испытуемых

выбрала бы правую дорожку, а половина - левую. Вероятность выбора каждой из

дорожек составляла бы 0,50.

Мы видим, что отклонения эмпирических частот от этой величины довольно

значительны. Возможно, различия между эмпирическим и теоретическим

распределением окажутся достоверными.

На Рис. 4.5 фактически представлены две гистограммы, но

столбики

Гистограмма - это диаграмма, в которой различная величина частот изображается различной высотой столбиков

(Плохинский Н. А., 1970, с. 14.)

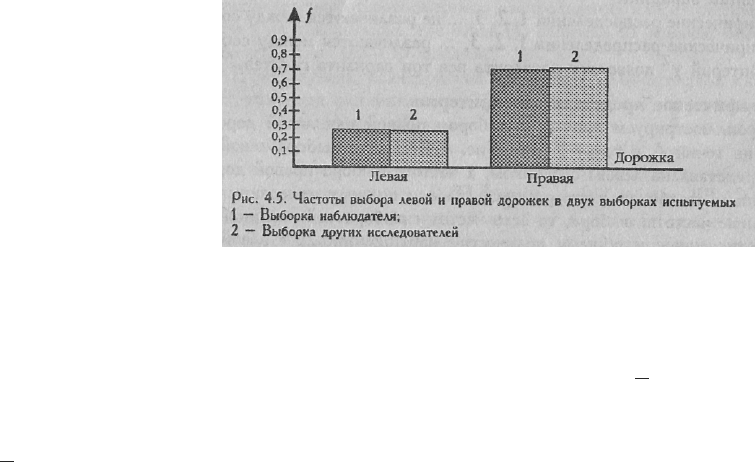
сгруппированы так, что слева сопоставляются частоты предпочтения левой дорожки в

выборе нашего наблюдателя (1) и в выборке Т.А. Доброхотовой и Н.Н. Брагиной (2),

а справа - частоты предпочтения правой дорожки в этих же двух выборках.

Мы видим, что расхождения между выборками очень незначительны. Критерий

χ2, скорей всего, подтвердит совпадение двух распределений.

Ограничения критерия

Объем выборки должен быть достаточно большим: п≥30. При п<30 критерий χ2

дает весьма приближенные значения. Точность критерия повышается при больших п.

2. Теоретическая частота для каждой ячейки таблицы не должна быть меньше 5:

5. Это означает, что если число разрядов задано заранее и не может быть

изменено, то мы не можем применять метод χ2, не накопив определенного

минимального числа наблюдений. Если, например, мы хотим проверить наши

предположения о том, что частота обращений в телефонную службу Доверия

неравномерно распределяются по 7 дням недели, то нам потребуется 5*7=35

обращений. Таким образом, если количество разрядов (k) задано заранее, как в

данном случае, минимальное число наблюдений (n

min

) определяется по формуле:

min

=k*5.

3. Выбранные разряды должны "вычерпывать" все распределение, то есть

охватывать весь диапазон вариативности признаков. При этом группировка на разряды

должна быть одинаковой во всех сопоставляемых распределениях.

4. Необходимо вносить "поправку на непрерывность" при сопоставлении

распределений признаков, которые принимают всего 2 значения. При внесении

поправки значение χ

уменьшается (см. Пример с по правкой на непрерывность).

5. Разряды должны быть неперекрещивающимися: если наблюдение отнесено

к одному разряду, то оно уже не может быть отнесено ни к какому другому разряду.

Сумма наблюдений по разрядам всегда должна быть равна общему количеству

наблюдений.

Правомерен вопрос о том, что считать числом наблюдений - количество выборов, реакций,

действий или количество испытуемых, которые совершают выбор, проявляют реакции или производят

действия. Если испытуемый проявляет несколько реакций, и все они регистрируются, то количество

испытуемых не будет совпадать с количеством реакций. Мы можем просуммировать реакции каждого

испытуемого, как, например, это делается

в методике Хекхаузена для исследования мотивации достижения

или в Тесте фрустрационной толерантности С. Розенцвейга, и сравнивать распределения индивидуальных

сумм реакций в нескольких выборках.

В этом случае числом наблюдений будет количество испытуемых. Если же мы подсчитываем частоту

реакций определенного типа в целом по выборке, то получаем распределение реакций разного типа, и

этом случае количеством наблюдений будет общее количество зарегистрированных реакций, а не

количество испытуемых.

С математической точки зрения правило независимости разрядов соблюдается в обоих случаях: одно

наблюдение относится к одному и только одному разряду распределения.

- Можно представить себе и такой вариант исследования, где мы изучаем распределение выборов

одного испытуемого. В

когнитивно-бихевиоральной терапии, например, клиенту предлагается всякий раз

фиксировать точной время появления нежелательной реакции, например, приступов страха, депрессии,

вспышек гнева, самоуничижающих мыслей и т. п. В дальнейшем психотерапевт анализирует полученные

данные, выявляя часы, в которые неблагоприятные симптомы проявляются чаще, и помогает клиенту

строить индивидуальную программу предупреждения неблагоприятных реакций.

Можно ли с помощью критерия χ2 доказать, что некоторые часы являются в этом

индивидуальном распределении более часто встречающимися, а другие - менее часто встречающимися?

Все наблюдения - зависимы, так как они относятся к одному и тому же испытуемому; в то же время все

разряды - неперекрещивающиеся, так

как один и тот же приступ относится к одному и только одному

разряду (в данном случае - часу дня). По-видимому, применение метода χ2 будет в данном случае

некоторым упрощением. Приступы страха, гнева или депрессии могут наступать неоднократно в течение

дня, и может оказаться так, что, скажем, ранний утренний, 6-часовой, и поздний

вечерний, 12-часовой,

приступы обычно появляются вместе, в один и тот же день: в то же время дневной 3-часовой приступ

появляется не ранее как через сутки после предыдущего приступа и не менее чем за двое суток до

следующего и т. п. По-видимому, речь здесь может идти о сложной математической модели

или вообще о

чем-то таком, чего нельзя "поверить алгеброй". И тем не менее в практических целях может оказаться

полезным использовать критерий для того, чтобы выявить систематическую неравномерность наступления

каких-либо значимых событий, выбора, предпочтений и т. п. у одного и того же человека.

Итак, одно и то же наблюдение должно

относиться только к одному разряду. Но считать ли

наблюдением каждого испытуемого или каждую исследуемую реакцию испытуемого - вопрос, решение

которого зависит от целей исследования (см.. напр., Ганзен В.А., Балин В.Д., 1991, с.10).

Главное же "ограничение" критерия χ

- то, что он кажется большинству

исследователей пугающе сложным.

Попытаемся преодолеть миф о непостижимой трудности критерия χ

. Чтобы

оживить изложение, рассмотрим шутливый литературный пример.

Шутливый пример

В гениальной комедии Н. В. Гоголя "Женитьба" у купеческой дочери Агафьи

Тихоновны было пятеро женихов. Одного она сразу исключила из рассмотрения,

потому что он был купеческого звания, как и она сама. А из остальных она не знала,

кого выбрать: "Уж как трудно решиться, так просто рассказать нельзя, как трудно. Если

бы

губы Никанора Ивановича да приставить к носу Ивана Кузьмича, да взять сколько-

нибудь развязности, какая у Балтазара Балтазарыча, да, пожалуй, прибавить к этому

еще дородности Ивана Павловича, я бы тогда тотчас решилась. А теперь поди

подумай! просто голова даже стала болеть. Я думаю, лучше всего кинуть жребий"

(Гоголь Н.В

., 1959, с. 487). И вот Агафья Тихоновна положила бумажки с четырьмя

именами в ридикюль, пошарила рукою в ридикюле и вынула вместо одного — всех!

Ей хотелось, чтобы жених совмещал в себе достоинства всех четверых, и, вынимая

все бумажки вместо одной, она бессознательно совершала процедуру выведения средней

величины. Но вывести среднюю величину из четверых людей невозможно, и Агафья

Тихоновна в смятении. Она влюблена, но не знает, в кого. "Такое несчастное положе-

ние девицы, особливо еще влюбленной" (там же, с. 487).

Вся беда в том, что ни Агафья Тихоновна, ни

ее тетушка, ни сваха Фекла

Ивановна не были знакомы с критерием χ2! Именно он мог бы им помочь в решении

их проблемы. С его помощью можно было бы попробовать установить, в кого больше

влюблена Агафья Тихоновна. Но для этого нам не нужно измерять губы Никанора

Ивановича или нос Ивана Кузьмича,

или объем талии дородного экзекутора Ивана

Павловича; не нужно нам и пускаться на какие-нибудь опасные эксперименты, чтобы

определить, насколько далеко простирается развязность Балтазара Балтазарыча. Мы

эти их достоинства принимаем как данность потому лишь, что они нравятся Агафье

Тихоновне. Мы принимаем их за разряды одного и того же признака, например,

направленности

взгляда Агафьи Тихоновны: сколько раз она взглянула на губы

Никанора Ивановича? На нос Ивана Кузьмича? Благосклонно взирала на дородного

Ивана Павловича или развязного Балтазара Бал-тазаровича? Внимательная сваха или

тетушка вполне могла бы этот признак наблюдать. Допустим, за полчаса смотрин ею

зафиксированы следующие наблюдения.

Агафья Тихоновна:

сидела с опущенными глазами 25

минут;

благосклонно смотрела на Никанора Ивановича 14 раз;

благосклонно смотрела на Ивана Кузьмича 5 раз;

благосклонно смотрела на Ивана Павловича 8 раз;

благосклонно смотрела на Балтазара Балтазарыча 5 раз.

Представим это в виде таблицы.

Таблица 4.1

Распределение взгляда Агафьи Тихоновны между 4 женихами

женихи

Никанор

Иванович

Иван

Кузьмич

Иван

Павлович

Балтазар

Балтазарыч

Всего

взглядов

Количество

взглядов

14 5 8 5 32

Теперь нам нужно сопоставить полученные эмпирические частоты с

теоретическими. Если Агафья Тихоновна никому не отдает предпочтения, то данное

распределение показателя направленности ее взгляда не будет отличаться от

равномерного распределения: она на всех смотрит примерно с одинаковой частотой. Но

если достоинства одного из женихов чаще притягивают ее взор, то это может быть

основанием для матримониального решения.

Гипотезы

: Распределение взглядов Агафьи Тихоновны между женихами не

отличается от равномерного распределения.

: Распределение взглядов Агафьи Тихоновны между женихами отличается от

равномерного распределения.

Теперь нам нужно определить теоретическую частоту взгляда при равномерном

распределении. Если бы все взгляды невесты распределялась равномерно между 4-мя

женихами, то, по-видимому, каждый из них получил бы по

всех ее взглядов.

Переведем эти рассуждения на более формализованный язык. Теоретическая

частота при сопоставлении эмпирического распределения с равномерным определяется

по формуле:

Все приведенные эмпирические частоты на самом деле пропорциональны количеству благосклонных высказываний

невесты о женихах в тексте пьесы.

где п - количество наблюдений;

к - количество разрядов признака.

В нашем случае признак - взгляд невесты, направленный на кого-либо из

женихов; количество разрядов признака - 4 направления взгляда, по количеству

женихов; количество наблюдений - 32.

Итак, в нашем случае:

Теперь мы будем сравнивать с этой теоретической частотой

все эмпирические

частоты.

На Рис. 4.6 сопоставления эмпирических частот с теоретической представлены

графически. Похоже, что области расхождений достаточно значительны, и Никанор

Иванович явно опережает других женихов. Иван Павлович еще может на что-то

надеяться, но для Ивана Кузьмича и Балтазара Балтазарыча отставка, по-видимому,

неизбежна.

Однако для того, чтобы доказать неравномерность полученного эмпирического

распределения,

нам необходимо произвести точные расчеты. В методе χ

они

производятся с точностью до сотых, а иногда и до тысячных долей единицы.

Расчеты будем производить в таблице по алгоритму.

АЛГОРИТМ 13

Расчет критерия χ2

Занести в таблицу наименования разрядов и соответствующие им эмпирические

частоты (первый столбец).

Рядом с каждой эмпирической частотой записать теоретическую частоту

(второй столбец).

Подсчитать разности между эмпирической и теоретической частотой по каждому

разряду (строке) и записать их в третий столбец.

4. Определить число степеней свободы по формуле:

ν=κ-1

где κ - количество разрядов признака.

Если ν=1, внести поправку на "непрерывность".

5. Возвести в квадрат полученные разности и занести их в четвертый столбец.

6. Разделить полученные квадраты разностей на теоретическую частоту и записать

результаты в пятый столбец.

7. Просуммировать значения пятого столбца. Полученную сумму обозначить как

ЭМП.

8. Определить по Табл. IX Приложения 1 критические значения для данного

числа степеней свободы V.

Если χ

эмп

меньше критического значения, расхождения между распределениями

статистически недостоверны.

Если χ

эмп

равно критическому значению или превышает его, расхождения между

распределениями статистически достоверны.

Все вычисления для данного случая отражены в Табл. 4.2.

Таблица 4.2

Расчет критерия χ2 при сопоставлении эмпирического распределения взгляда Агафьи

Тихоновны между женихами с равномерным распределением

Разряды - женихи Эмпирическая

частота взгляда

(

)

Теоретическая

частота

(

)

эj

-f

) (f

эj

-f

)

эj

-f

)

/ f

Никанор

Иванович

Иван

Кузьмич

Иван

Павлович

Балтазар

Балтазарыч

-3

4.500

1.125

ммы 32 32 0 6.750

Может показаться, что удобнее суммировать все возведенные в квадрат разности

между эмпирическими и теоретическими частотами, а затем уже эту сумму разделить

на f

. В данном случае это возможно, так как f

для всех разрядов одинакова. Однако

позже мы увидим, что так бывает далеко не всегда. Нужно быть внимательными или,

экономя свое внимание, просто взять за правило всякий раз вычислять (f

эi

—f

)

до

суммирования.

Необходимо также всякий раз убеждаться в том, что сумма разностей между

эмпирическими и теоретической частотами (сумма по третьему столбцу) равна 0. Если

это равенство не соблюдается, это означает, что в подсчете частот или разностей

допущена ошибка. Необходимо найти и устранить ее прежде чем переходить к

дальнейшим расчетам.

Алгоритм вычислений, таким

образом, выражается формулой:

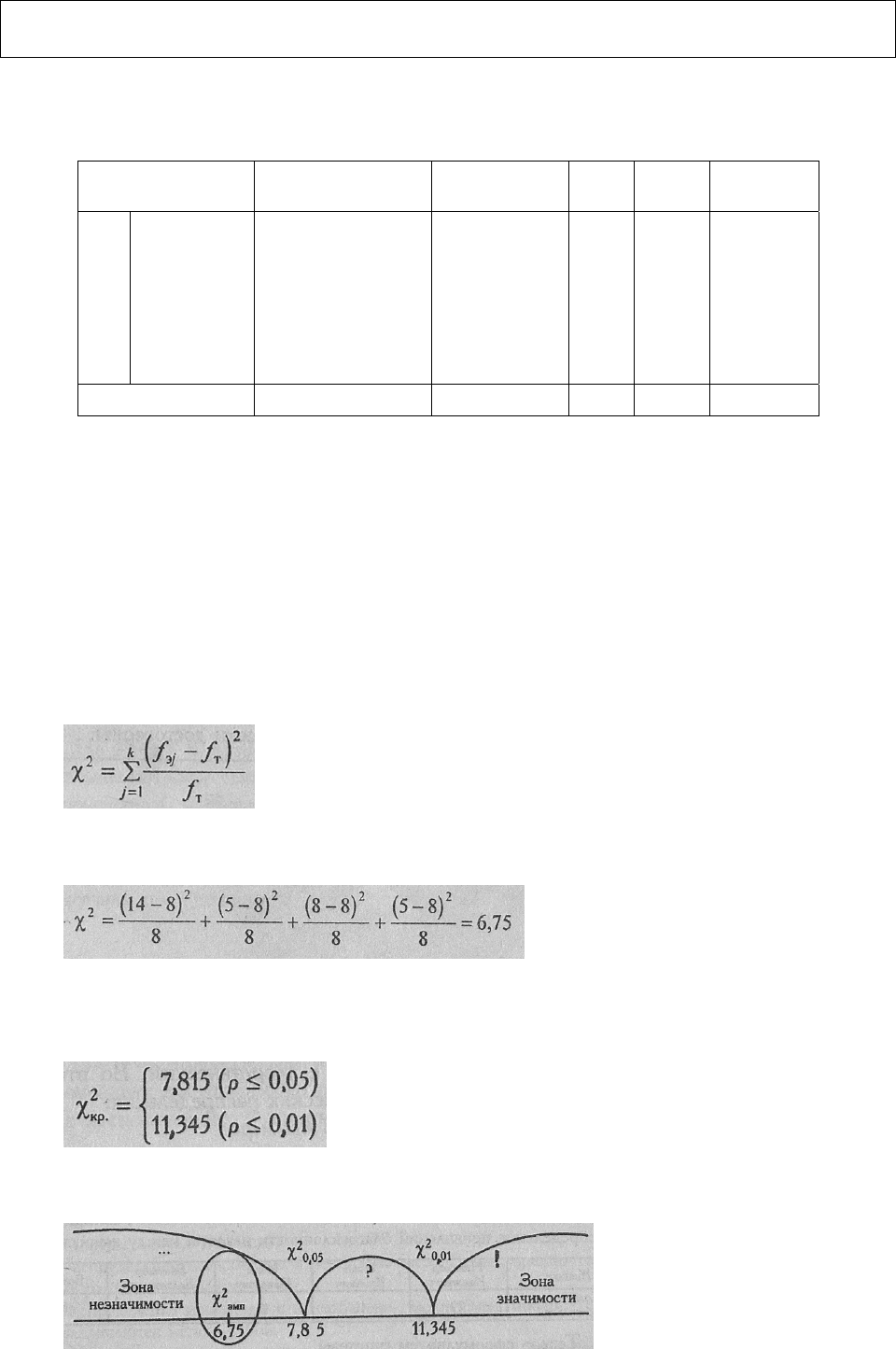
где f

эj

- эмпирическая частота по j-тому разряду признака; f

- теоретическая

частота; j - порядковый номер разряда; k - количество разрядов признака. В данном

случае:

Для того, чтобы установить критические значения % , нам нужно определить

число степеней свободы V по формуле: ν= k-l

где k - количество разрядов. В нашем случае ν=4—1=3. По Табл. IX Приложения

1 определяем:

Построим "ось значимости". Ясно, что чем больше отклонения эмпирических

частот от теоретической, тем больше будет величина χ2 . Поэтому зона значимости

располагается справа, а зона незначимости -слева.

К сожалению, на основании этих данных тетушка не сможет дать Агафье

Тихоновне обоснованного ответа:

эмп

<χ

кр

Ответ: Н

принимается. Распределение взгляда Агафьи Тихоновны между

женихами не отличается от равномерного распределения.

Но, допустим, тетушка на этом не успокоилась. Она стала внимательно следить за

тем, сколько раз племянница упомянет в разговоре каждого из женихов. Допустим, ею

получено следующее распределение упоминаний Агафьей Тихоновной женихов и их

достоинств:

Никанор Иванович - 15 раз,

Иван Кузьмич

- 6 раз,

Иван Павлович - 9 раз,

Балтазар Балтазарыч - 6 раз.

Тетушка уже видит, что похоже, Никанор Иванович ("уж такой великатный, а

губы, мать моя, - малина, совсем малина") пользуется большей благосклонностью

Агафьи Тихоновны, чем все остальные женихи. У нее есть два пути, чтобы это

доказать статистически.

1) Суммировать все проявления благосклонности со стороны невесты: взгляды

упоминания в разговоре, - и сопоставить полученное распределение с равномерным.

Поскольку количество наблюдений возросло, есть шанс, что различия окажутся

достоверными.

2) Сопоставить два эмпирических распределения - взгляда и упоминаний в

разговоре, - с тем, чтобы показать, что они совпадают между собой, то есть и во

взглядах, и в словах Агафья Тихоновна придерживается одинаковой системы

предпочтений. Проанализируем оба варианта сопоставлений. В первом случае мы

будем решать уже известную нам задачу сопоставления эмпирического распределения

с теоретическим. Во втором случае мы будем сопоставлять два эмпирических

распределения.

Первый вариант развития шутливого примера: увеличение количества

наблюдений

Вначале создадим таблицу эмпирических частот, в которой будут суммированы

все замеченные проявления благосклонности невесты.

Таблица 4.3

Распределение проявлений благосклонности невесты между женихами

Женихи Никанор

Иванович

Иван

зьмич

Иван

Павлович

Балтазар

Балтазарыч

Всего

Количество

проявлений

29 11 17 11 68

Теперь сформулируем гипотезы.

: Распределение проявлений благосклонности невесты (взгляды и упоминания в

разговоре) не отличается от равномерного распределения. H

: Распределение

проявлений благосклонности невесты отличается от равномерного распределения.. Все

расчеты произведем в таблице по алгоритму.

Таблица 4.4

Расчет критерия χ2 при сопоставлении проявлений благосклонности Агафьи Тихоновны

с равномерным распределением

Разряды -

женихи

Эмпирические

частоты

Теоретическая

частота

суммарных

проявлений

эj

-f

)(f

эj

-f

)

эj

-f

)

/ f

Ник. Ив.

Ив. Куз.

Ив. Пав.

Бал. Бал.

-6

144

8,47

2,12

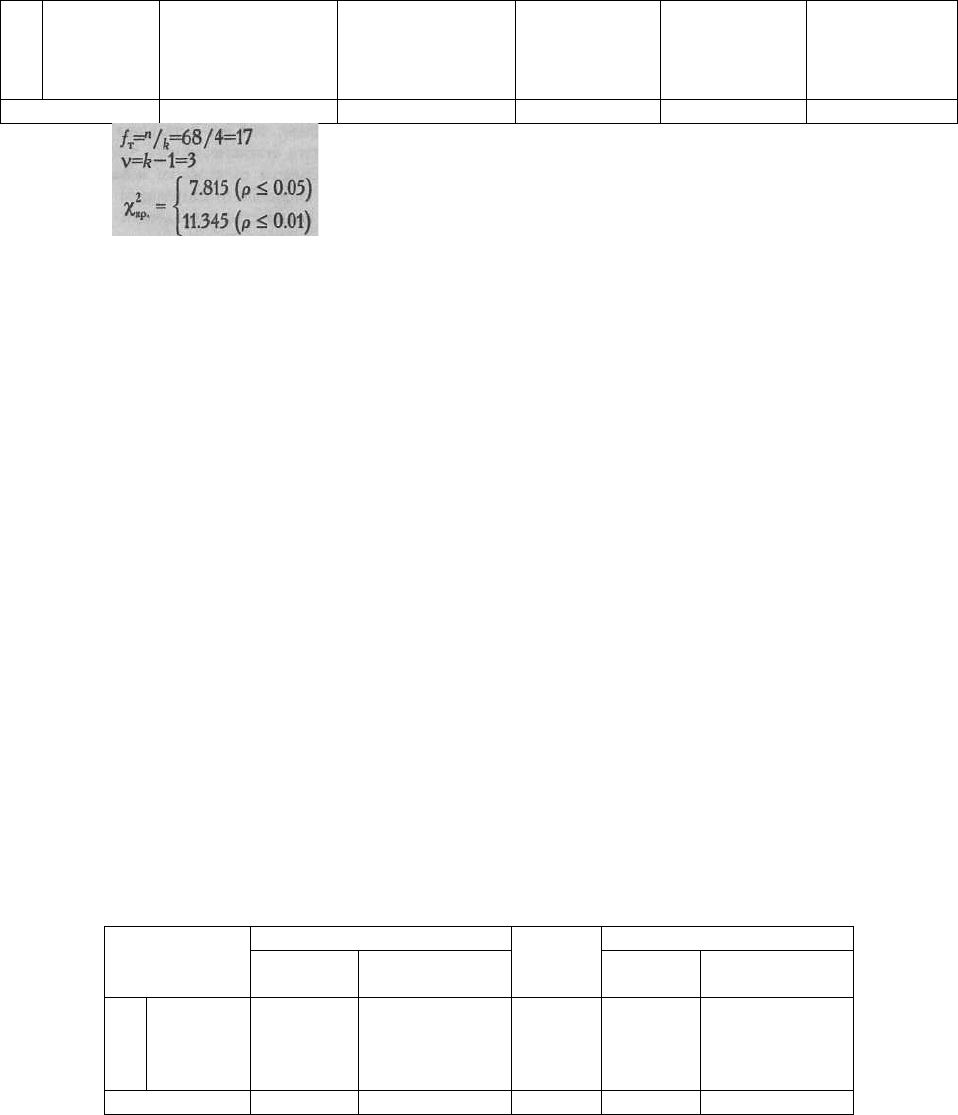
Суммы 68 68 0 12,71

эмп

=12,71

эмп

> χ

кр.

Ответ: H

отклоняется, принимается Н

. Распределение проявлений

благосклонности невесты между женихами отличается от равномерного распределения

(р<0,01).

На этом примере мы убедились, что увеличение числа наблюдений повышает

достоверность результата, если, конечно, в новых наблюдениях воспроизводится

прежняя тенденция различий.

Второй вариант развития шутливого примера: сопоставление двух эмпирических

распределений

Теперь мы должны ответить на вопрос, одинаковая ли система предпочтений

проявляется во взгляде Агафьи Тихоновны и ее словах?

Сформулируем гипотезы. Н

: Распределения невербально и вербально

выражаемых предпочтений не различаются между собой.

: Распределения невербально и вербально выражаемых предпочтений

различаются между собой.

Для подсчета теоретических частот нам теперь придется составить специальную

таблицу (Табл. 4.5). Ячейки в двух столбцах слева обозначим буквами. Для каждой из

них теперь будет подсчитана особая, только к данной ячейке относящаяся,

теоретическая частота. Это обусловлено тем, что количества взглядов и словесных

отзывов невесты о женихах неравны; взглядов 32, а словесных отзывов - 36. Мы

должны всякий раз учитывать эту пропорцию.

Таблица 4.5

Эмпирические и теоретические частоты взглядов и упоминаний о жениха

Разряды -

женихи

Эмпирические частоты Суммы Теоретические частоты

взгляда Упоминаний в

разговоре

взгляда Упоминаний в

разговоре

Ник. Ив.

Ив. Куз.

Ив. Пав.

Бал. Бал.

14 А

5 В

8 Д

5 Ж

15 Б

6 Г

9 Е

6 З

13,63 А

5,17 В

7,99 Д

5,17 Ж

15,37 Б

5,83 Г

9,01 Е

5,83 З

Суммы 32 36 68 32 36

Рассчитаем эту пропорцию. Всего проявлений благосклонности отмечено 68, из

них 32 - взгляды и 36 - словесные высказывания. Доля взглядов составит

32/68=0,47; доля упоминаний - 36/68=0,53.

Итак, во всех строках взгляды должны были бы составлять 0,47 всех проявлений

по данной строке, а упоминания в разговоре - 0,53 всех проявлений. Теперь, зная

суммы проявлений по каждой строке, мы можем рассчитать теоретические частоты для

каждой ячейки Табл. 4.5.

Атеор

=29*0,47=13,63

Бтеор

=29*0,53=15,37

Втеор

=11*0,47=5,17

Гтеор

=11*0,53=5,83

теор

=17*0,47=7,99