Сибирева А.Р. Высшая математика для студентов технических специальностей в формулах и таблицах
Подождите немного. Документ загружается.

Федеральное агентство по образованию
Государственное образовательное учреждение
высшего профессионального образования
Ульяновский государственный технический университет
ВЫСШАЯ МАТЕМАТИКА
для студентов технических специальностей
В ФОРМУЛАХ И ТАБЛИЦАХ
( часть 1)
Методические указания
Составитель: А. Р. Сибирева
Ульяновск 2007

2
УДК 517 (076)
ББК 22.161я7
Рецензент доцент кафедры «Математический анализ» УгПУ, кандидат
физико-математических наук Е. В. Фолиадова
Одобрено секцией методических пособий научно-методического совета
университета
Высшая математика для студентов технических специальностей в формулах
и таблицах: методические указания / сост.: А. Р. Сибирева. – Ульяновск:
УлГТУ, 2007. – 34 с.
Указания составлены в соответствии с учебной программой курса "Высшая математика" для сту-
дентов технических специальностей втуза.
Настоящие методические указания являются справочным материалом. Они содержат определения,
формулы, некоторые теоретические сведения, алгоритмы решения типовых задач. Цель работы – предста-
вить в небольшом по объему справочнике некоторые сведения по математике, необходимые при изучении
тем «Матрицы
», «Системы линейных уравнений», «Элементы аналитической геометрии», «Пределы и не-
прерывность», «Дифференциальное исчисление функций одной переменной», «Интегральное исчисление
функций одной переменной», «Дифференциальные уравнения».
Методические указания могут быть использованы студентами технических специальностей при ре-
шении задач курса «Высшая математика».
Работа подготовлена на кафедре «Высшая математика».
УДК 517 (076)
ББК
22.161я7
© Сибирева А. Р., составление, 2007
© Оформление. УлГТУ, 2007

3
ПРЕДИСЛОВИЕ
Данные методические указания являются справочным материалом.
Они содержат определения, формулы, некоторые теоретические сведения,
алгоритмы решения типовых задач. Цель работы – представить в небольшом
по объему справочнике некоторые сведения по математике, необходимые
при изучении тем «Матрицы», «Системы линейных уравнений», «Элементы
аналитической геометрии», «Пределы и непрерывность», «Дифференциаль-
ное исчисление функций одной переменной», «Интегральное исчисление
функций одной переменной», «Дифференциальные уравнения».
Методические указания могут быть использованы студентами техниче-
ских специальностей при решении задач курса «Высшая математика». Сле-
дует иметь в виду, что это – не учебная книга, не краткий конспект лекций.
Краткий справочный материал не заменит изучения лекционного материала
и учебной литературы.
1. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
1.1. Матрица
Матрицей размера nm × называют прямоугольную таблицу чисел, со-
держащую т строк и п столбцов. Обозначения
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎝
⎛
=
mnmm
n
n
a...aa
....
a...aa
a...aa
A
21
22221
11211
,
(
)
nm
ij
aA
×
=
.
Суммой двух матриц
(
)
nm
ij
aA
×
=
и
(
)
nm
ij
bB
×
=
одинаковых размеров nm
×
называется матрица тех же размеров
(
)
(
)
(
)
nm
ijij
nm
ij
nm
ij
babaBA
×××
+
=
+
=
+ .
Произведением n×1 строки на 1
×
n столбец называют число равное
()
.ba...baba
b
...
b
b
a...aa
nn
n
n
+++=
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎝
⎛
⋅
2211
2
1
21
Произведением двух матриц
(
)
nm
ij
aA
×
=
и
(
)
pn
ij
bB
×
=
, которые заданы в
определенном порядке (первая и вторая) и размеры которых связаны услови-
ем: число столбцов первой матрицы равно числу строк – второй, называется
матрица
(
)
pm
ij
cC
×
= , каждый элемент
ij
c которой равен произведению i -ой
строки матрицы
A
на
j
-ый столбец матрицы
B
.
Произведением матрицы
(
)
nm
ij
aA
×
=
на число
c
называется матрица, по-
лучаемая умножением всех элементов матрицы
A
на число c :
(
)
nm
ij
cacA
×
=
.
Транспонированием матрицы называется перемена ролями строк и
столбцов с сохранением их номеров.

4
1.2. Определители
Определителем второго порядка называют число
21122211
2221
1211
aaaa
aa
aa
Adet −==
.
Определителем третьего порядка называют число
.aaaaaaaaa
aaaaaaaaa
aaa
aaa
aaa
Adet
113223332112312213
133221312312332211
333231
232221
131211
−−−
−++==
Минором
ij
M элемента
ij
a матрицы )nn(A
×
называется определитель
порядка 1−n , полученный вычеркиванием i -ой строки и
j
-го столбца, в пе-
ресечении которых стоит данный элемент
ij
a .
Алгебраическим дополнением элемента
ij
a , называется число
(
)
ij
ji
ij
MA
+
−= 1 .
Определитель равен сумме произведений элементов любой его строки
(или столбца) на их алгебраические дополнения.
Простейшие свойства определителей.
1. При транспонировании определителя его значение не изменяется.
2. Если все элементы какой-нибудь строки (или столбца) определителя
равны нулю, то определитель равен нулю.
3. При перестановке двух любых строк (или столбцов) определитель ме-
няет знак.
4. Если две строки (или два столбца) определителя одинаковы, то он ра-
вен нулю.
5. Если все элементы одной строки (или столбца) определителя умножить
на одно и то же число, то и весь определитель умножится на это число. Ины-
ми словами, общий множитель всех элементов строки (или столбца) можно
выносить за знак определителя.
6. Если все элементы одной строки определителя пропорциональны соот-
ветствующим элементам другой строки, то определитель равен нулю. То же
верно и для столбцов.
7. Если к одной строке определителя прибавить другую строку, умножен-
ную на любое число, то значение определителя не изменится. То же верно и
для столбцов.
1.3. Обратная матрица
Определение. Обратной матрицей для квадратной nn × матрицы
A
на-
зывается квадратная матрица
1−
A того же порядка, обладающая свойством
E
AAAA
=
⋅
=
⋅
−− 11
,
где
E
— единичная матрица порядка n ,

5
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎝
⎛
=
1000
010
001
....
...
...
E
.
Квадратная матрица А называется вырожденной, если ее определитель
равен нулю. Невырожденной, если ее определитель не равен нулю.
Теорема. Вырожденная матрица не имеет обратной.
Любая невырожденная матрица
(
)
nn
ij
aA
×
=
имеет единственную обрат-
ную матрицу
T
nnnn
n
n
A...AA
....
A...AA
A...AA
Adet
A
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎝
⎛
=
−
21
22221
11211
1
1
,
где
ij
A – алгебраическое дополнение элемента
ij
a ,
T
– знак транспонирования.
1.4. Система линейных уравнений
Рассмотрим систему линейных уравнений
⎪
⎪
⎩
⎪
⎪
⎨
⎧
=+++
=+++
=+++
.bxa...xaxa
..........................................
,bxa...xaxa
,bxa...xaxa
mnmnmm
nn
nn
2211
22222121
11212111
(1)
Система линейных уравнений может быть записана в виде
B
A
X
=
,
где
(
)
nm
ij
aA
×
= ,
(
)
1×
=
m
i
bB ,
()
1×
=
n
i
xX ,
или в виде расширенной матрицы
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎝
⎛
mmnmm
n
n
b
...
b
b
a...aa
....
a...aa
a...aa
2
1
21
22221
11211
. (2)
Метод Крамера решения системы линейных уравнений. Если дана
система уравнений (1), где nm
=
(т. е. число уравнений равно числу неиз-
вестных) и определитель
0
≠
Adet
, то система имеет единственное решение,
которое находится по формулам Крамера
∆
∆
=
i
i
x
( n,...,,i 21
=
),
где Adet=∆ , определитель
i
∆
получен из определителя ∆ заменой
i
-го
столбца на столбец из свободных членов.
Матричный метод решения системы линейных уравнений. Если
дана система уравнений (1), где nm
=
(т. е. число уравнений равно числу не-

6
известных) и определитель 0
≠
Adet , то система имеет единственное решение,
которое находится по формуле
B
A
X
1−
=
.
Метод Гаусса решения системы линейных уравнений.
Рангом системы строк (соответственно столбцов) матрицы А называет-
ся наибольшее число линейно независимых среди них.
Элементарными преобразованиями матрицы называются следующие
преобразования: 1) перестановка двух любых строк, 2) умножение строки на
число c , отличное от нуля, 3) прибавление к одной строке другой строки,
умноженной на любое число.
Две матрицы называются эквивалентными, если от одной из них к дру-
гой можно перейти путем конечного числа элементарных преобразований.
При элементарных преобразованиях матрицы ее ранг не изменяется,
иными словами, ранги эквивалентных матриц равны.
Ступенчатой матрицей называется матрица, обладающая тем свойст-
вом, что если в какой-либо из ее строк первый отличный от нуля элемент
стоит на k -ом месте, то во всех следующих строках на первых k местах сто-
ят нули.
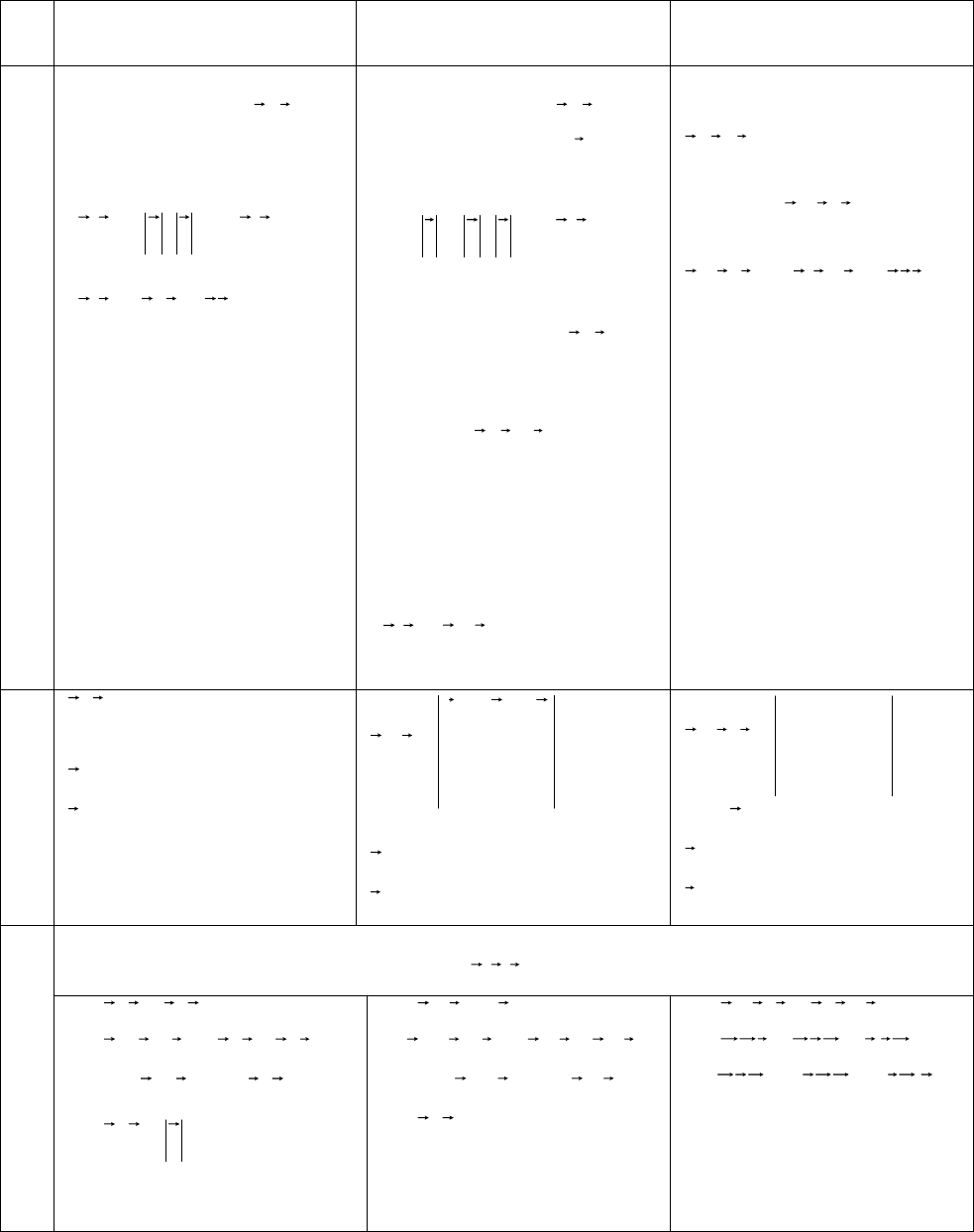
Алгоритм решения системы линейных уравнений методом Гаусса.
1. Записать расширенную матрицу B/A ,отвечающую системе уравнений (1).
2. Элементарными преобразованиями привести расширенную матрицу B/A
к ступенчатому виду.
3. Провести исследование совместности системы линейных уравнений, ис-
пользуя теорему Кронекера-Капелли:
а) если
nB/rangArangA ==
, где n число неизвестных, то система линейных
уравнений имеет единственное решение;
б) если nB/rangArangA <= , где n число неизвестных, то система линейных
уравнений имеет бесконечно много решений;
в) если B/rangArangA ≠ , то система линейных уравнений не имеет реше-
ний.
4. Записать ступенчатую систему линейных уравнений.
а) Если nB/rangArangA == , последовательно найти
11
x,...,x,x
nn −
.
б) Случай nB/rangArangA
<
= . Неизвестные, с которых начинаются урав-
нения ступенчатой системы, назовем базисными переменными (существует
более общий способ выбора базисных переменных). Остальные переменные
назовем свободными. Выразим базисные переменные через свободные, полу-
чим тем самым общее решение системы уравнений.
в) Если B/rangArangA ≠ , то система линейных уравнений не имеет реше-
ний.
7
2. ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ
2.1. Векторы. Основные определения, понятия темы «Векторы» см., напри-
мер, [ 1,2].
2.2. Скалярное, векторное, смешанное произведение векторов
Скалярное произве-
дение
Векторное произве-
дение
Смешанное произве-
дение
Определение
Скалярным произведе-
нием векторов
a
,
b
на-
зывается число, оп-
ределяемое равенством
)b,acos(ba)b,a(
∧
⋅= .
Обозначения:
)b,a( , ba,ba ⋅ .
Векторным произведе-
нием векторов
a
,
b
на-
зывается вектор
c
,
длина которого равна
)b,asin(bac
∧
⋅=
,
а направление таково,
что он ортогонален пло-
скости векторов
a
,
b
и
образует с ними правую
тройку векторов (т.е.
векторы
a
,
b
,
c
направ-
лены, соответственно,
как большой, указа-
тельный и средний
пальцы правой руки).
Обозначения:
]b,a[ , ba × .
Смешанным произве-
дением векторов
a
,
b
,
c
называется чис-
ло равное
cba ⋅× .
Обозначения:
cba ⋅× , )c],b,a([ , cba .
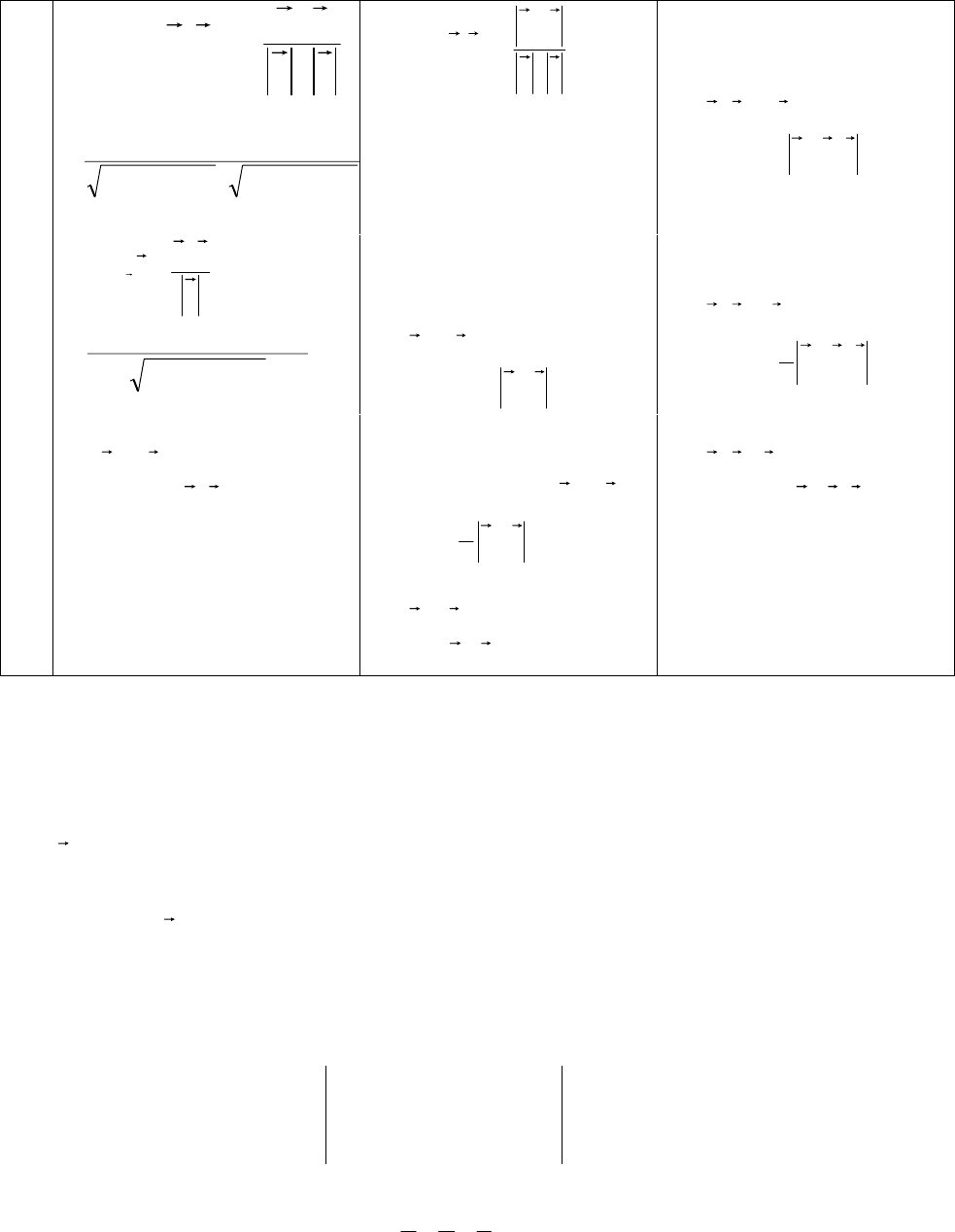
Формулы
212121
zzyyxxba ⋅+⋅+⋅=⋅ ,
где
)z,y,x(a
111
=
,
)z,y,x(b
222
= .
222
111
zyx
zyx
kji
ba =×
,
где
)z,y,x(a
111
=
,
)z,y,x(b
222
= .
333
222
111
zyx
zyx
zyx
cba =⋅×
,
где
)z,y,x(a
111
= ,
)z,y,x(b
222
=
,
)z,y,x(c
333
= .
Для любых векторов
c,b,a , для любого числа
∈
λ
R
R
Свойства
1) abba ⋅=⋅ ,
2)
caba)cb(a ⋅+⋅=+⋅ ,
3)
)ab(b)a( ⋅⋅=⋅⋅
λλ
,
4)
2
aaa =⋅ .
1)
abba ×−=× ,
2)
caba)cb(a ×+×=+× ,
3)
)ba(b)a( ×⋅=×⋅
λλ
,
4)
0=⋅aa .
1)
cbacba ×⋅=⋅× ,
2)
=== acbbaccba
abcbcacab −=−=−=
3) Если два вектора в
смешанном произведе-
нии поменять местами,
то его знак изменится.
8
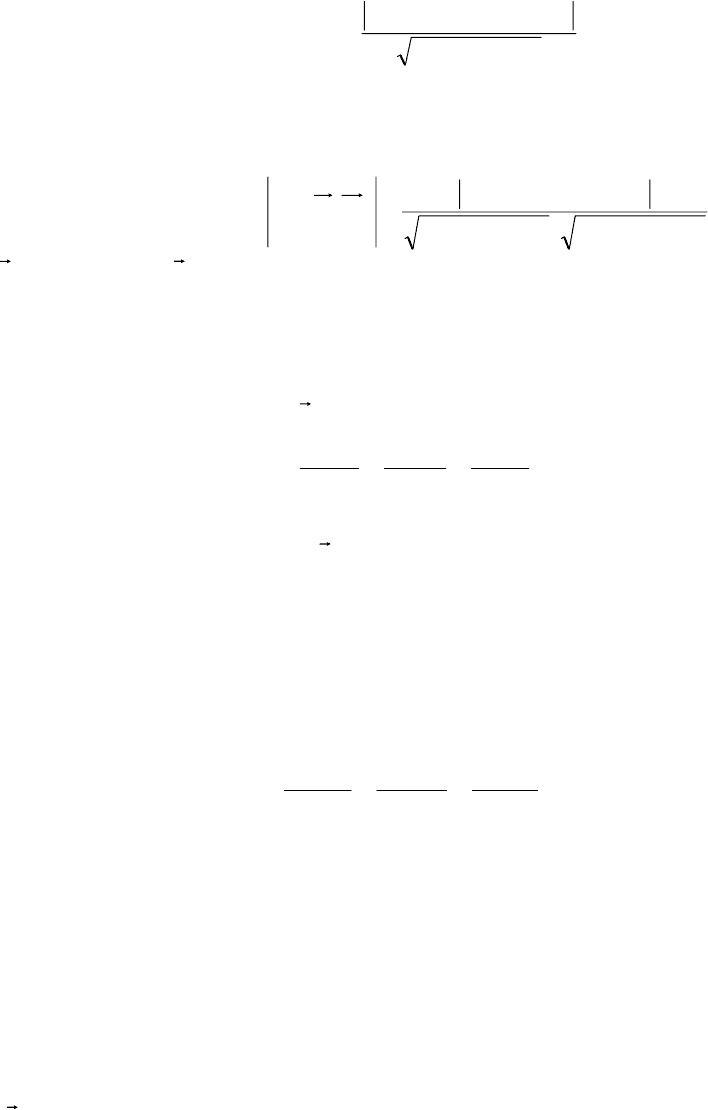
1)
=
⋅
⋅
=
∧
ba
ba
)b,acos(
2
2
2
2
2
2
2
1
2
1
2
1
212121
zyxzyx
zzyyxx
++⋅++
⋅+
⋅
+⋅
=
1)
ba
ba
)b,asin(
⋅
×
=
∧
.
1) Объем параллеле-
пипеда, построенно-
го на векторах
a
,
b
и
c
cbaV ⋅×= .
2) =
⋅
=
a
ba
bпр
a
2
1
2
1
2
1
212121
zyx
zzyyxx
++
⋅+⋅+⋅
=
2) Площадь паралле-
лограмма, постро-
енного на векторах
a
и
b
baS ×= .
2) Объем тетраэдра,
построенного на
a
,
b
и
c
cbaV ⋅×=
6
1
.
Приложения
3) (Ненулевые векторы
a
и
b
ортогональ-
ны)
)ba( 0=⋅⇔
3) Площадь треуголь-
ника, построенного
на векторах
a
и
b
baS ×=
∆
2
1
.
4) (Ненулевые векторы
a
и
b
коллинеарны)
)ba( 0
r
=×⇔
.
3) (Ненулевые векторы
a
,
b
,
c
компланар-
ны)
)cba( 0=⋅×⇔ .
2.3. Уравнение плоскости
1. Общее уравнение плоскости
0
=
+
+
+
DCzByAx ,
где
)C,B,A(n = – нормальный вектор плоскости.
2. Уравнение плоскости, проходящей через точку
)z,y,x(M
000
, с нормальным
вектором
)C,B,A(n =
0
000
=
−
+
−
+
− )zz(C)yy(B)xx(A .
3. Уравнение плоскости, проходящей через три точки
)z,y,x(M
1111
,
)z,y,x(M
2222
, )z,y,x(M
3333
0
131313
121212
111
=
−−−
−−−
−−−
zzyyxx
zzyyxx
zzyyxx
.
4. Уравнение плоскости в отрезках
1=++
c
z
b
y
a
x
,
где
a , b , c – отрезки, отсекаемых плоскостью на осях OX ,OY , OZ , соответст-
венно.
5. Нормальное уравнение плоскости
0
=
−
⋅
+
⋅
+
⋅ pzcosycosxcos
γ
β
α
,
9
где
α
cos ,
β
cos ,
γ
cos – направляющие косинусы перпендикуляра, опущенно-
го из начала координат на заданную плоскость,
p
– расстояние от начала ко-
ординат до плоскости.
Расстояние от точки
)z,y,x(M
mmm
до плоскости P, заданной уравнением
0
=
+
+
+
DCzByAx ,
находится по формуле
222
CBA
DCzByAx
)P,M(
mmm
++
+++
=
ρ
.
Косинус угла между плоскостями
0
1111
=
+
++ DzCyBxA и 0
2222
=
+
+
+
DzCyBxA
находится по формуле
2
2
2
2
2
2
2
1
2
1
2
1
212121
21
CBACBA
CCBBAA
)n,ncos(cos
++++
++
==
∧
α
,
где
)C,B,A(n
111
1
= , )C,B,A(n
222
2
= – нормальные векторы плоскостей.
2.4. Прямая в пространстве
1. Каноническое уравнение прямой, проходящей через точку
)z,y,x(M
000
, с
направляющим вектором
)m;l;k(q =
m
zz
l
yy
k
xx
000
−
=
−
=
−
.
2. Параметрические уравнения прямой, проходящей через точку )z,y,x(M
000
,
с направляющим вектором
)m;l;k(q =
⎪
⎩
⎪
⎨
⎧
+=
+=
+=
,mtzz
,ltyy
,ktxx
0
0
0
(
∈
t R).
3. Уравнение прямой, проходящей через две точки
)z,y,x(M
1111
и
)z,y,x(M
2222
12
1
12
1
12
1
zz
zz
yy
yy
xx
xx
−
−
=
−
−
=
−
−
.
4. Прямая, как линия пересечения двух плоскостей
⎩
⎨
⎧
=+++
=+++
.DzCyBxA
,DzCyBxA
0
0
2222
1111
2.5. Прямая на плоскости
1. Общее уравнение прямой
0
=
+
+
CByAx ,
где
)B,A(n = – нормальный вектор прямой.

10
2. Уравнение прямой, проходящей через точку )y,x(M
00
с нормальным век-
тором
)B,A(n =
0
00
=
−
+
−
)yy(B)xx(A .
3. Каноническое уравнение прямой
m
yy
l
xx
00
−
=
−
,
где
)y,x(M
00
– точка прямой, )m;l(q = – направляющий вектор прямой.
4. Параметрические уравнения прямой
⎩
⎨
⎧
+=
+=
,mtyy
,ltxx
0
0
(
∈
t R),
где
)y,x(M
00
точка прямой, )m;l(q = – направляющий вектор прямой.
5. Уравнение прямой, проходящей через две точки
)y,x(M
111
и
)y,x(M
222
12
1
12
1
yy
yy
xx
xx
−
−
=
−
−
.
6. Уравнение прямой в отрезках
1=+
b
y
a
x
,
где
a и b – отрезки, отсекаемые прямой на осях OX и OY , соответственно.
7. Нормальное уравнение прямой
0
=
−
⋅
+
⋅
pycosxcos
β
α
,
где
α
cos ,
β
cos – направляющие косинусы перпендикуляра, опущенного из
начала координат на заданную прямую,
p
– расстояние от начала координат
до прямой.
8. Уравнение прямой с угловым коэффициентом
bkxy
+
=
,
где
α
tgk = ,
α
– угол между прямой и положительным направлением оси OX ,
)b;( 0
– точка пересечения прямой с осью OY .
Расстояние от точки
)y,x(M
mm
до прямой l , заданной уравнением
0
=
+
+
CByAx ,
находится по формуле
22
BA
CByAx
)l,M(
mm
+
++
=
ρ
.
Косинус угла между прямыми
0
111
=
+
+ CyBxA и 0
222
=
+
+
CyBxA
находится по формуле
2
2
2
2
2
1
2
1
2121
21
BABA
BBAA
)n,ncos(cos
++
+
==
∧
α
,
где
)B,A(n
11
1
= , )B,A(n
22
2
= – нормальные векторы прямых.
