Сибирева А.Р. Высшая математика для студентов технических специальностей в формулах и таблицах
Подождите немного. Документ загружается.


11
3. ПРЕДЕЛЫ И НЕПРЕРЫВНОСТЬ
3.1. Определение предела последовательности и предела функции см. [3,5].
3.2. Свойства пределов.
Если функции
)(xfy =
,
)(xgy
=
имеют конечные пределы при a
x
→
(
a – конечное число или ∞ ), то
1.
)x(glim)x(flim))x(g)x(f(lim
axaxax →→→
+
=
+ ,
2.
)x(glim)x(flim))x(g)x(f(lim
axaxax →→→
⋅
=
⋅ ,
3.
)x(glim/)x(flim))x(g/)x(f(lim
axaxax →→→
=
))x(glim(
ax
0
≠
→
,
4.
)x(flimc))x(fc(lim
axax →→
⋅=⋅ )( constc
=
,
5.
cclim
ax
=
→
)( constc = ,
6.
)x(glim
ax
)x(g
ax
ax
))x(flim())x(f(lim
→
→→
= .
3.3. Особые случаи
1. Для любого
∈a R, ∞≠a
+
∞=∞+=+∞+ aa ,
−
∞
=
−
∞
+
=
+∞− )(aa ,
+
∞
=
∞
+
∞
+
,
−
∞=∞−∞− .
2. Если
0>a , то
+
∞
=
+∞⋅ )(a ,
−
∞
=
−
∞
⋅
)(a .
Если
0<a
, то
−
∞
=
+∞⋅ )(a ,
+
∞
=
−
∞
⋅
)(a .
+∞=+∞⋅+∞ )()( ,
+
∞
=
−
∞
⋅
−
∞ )()( , −∞=
+
∞
⋅
−
∞ )()( .
3. Для любого
∈a R, ∞≠a
0=
∞−
=
∞+
aa
.
Для любого
∈a R, 0≠a
∞=
0
a
.
4.
⎪
⎩
⎪
⎨
⎧
=
<<
>∞+
=
∞+
.a
,a,
,a,
a
1 если нность,неопределе
10 если 0
1 если
(3)
∞+∞−
= )
1
(
a
a
(используй (3)).
3.4. Неопределенности
0
0
;
∞
∞
;
∞
⋅
0 ;
∞
−
∞
;
∞
1 ;
0
∞
;
0
0
.
3.5. Замечательные пределы
Первый замечательный предел
1
0
=
→
x
xsin
lim
x
. (4)
Второй замечательный предел
exlim
x
x
=+
→
1
0
)1( , e
x
lim
x
x
=+
∞→
)
1
1( . (5)
12
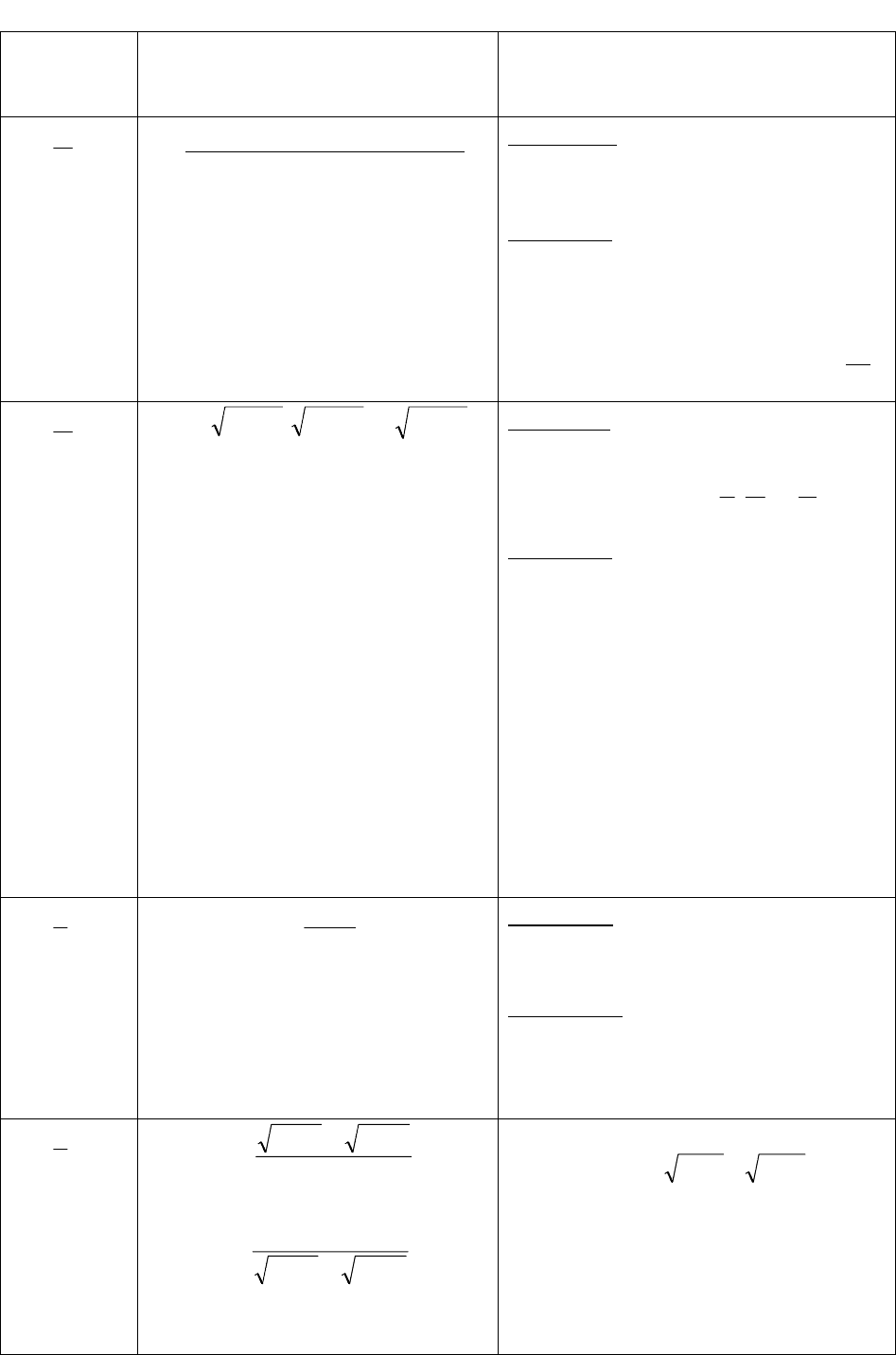
3.6. Раскрытие неопределенностей
Вид неоп-
ределен-
ности
Предел Способ нахождения предела
1.
∞
∞
mm
mm
nn
nn
x
bxb...xbxb
axa...xaxa
lim
++++
++++
−
−
−
−
∞→
1
1
10
1
1
10
1 способ. Числитель и знамена-
тель дроби разделить почленно
на
α
x
, где },max{ nm
=
α
.
2 способ.
Воспользоваться теоремой.
а) Если
mn
<
, то предел равен
0
.
б) Если
mn > ,то предел равен
∞
.
в)Если
mn
=
,то предел равен
0
0
b
a
.
2.
∞
∞
))x(T,...,)x(Q,)x(P(Rlim
q
p
m
l
n
k
x ∞→
,
где
)(),...,(),( xTxQxP
plk
– много-
члены степеней
plk ,..,, , соот-
ветственно,
R
– дробно-
рациональная функция от
корней
1 способ
. Числитель и знамена-
тель дроби разделить почленно
на
α
x , где
⎭
⎬
⎫
⎩
⎨
⎧
=
q
p
m
l
n
k
,...,,max
α
.
2 способ.
а) Если старшая степень числи-
теля больше старшей степени
знаменателя, то предел равен
∞
.
б) Если старшая степень числи-
теля меньше старшей степени
знаменателя, то предел равен 0.
в) Если старшие степени числи-
теля и знаменателя равны, то
предел равен отношению коэф-
фициентов (с учетом корней)
при старших степенях.
3.
0
0
)x(Q
)x(P
lim
ax→
,
где
)(xP
и
)(xQ
– многочлены
1 способ.
Разложить числитель и
знаменатель на множители, со-
кратить общие множители.
2 способ.
Делить числитель и
знаменатель на
)( ax − столько
раз, сколько потребуется, чтобы
не стало неопределенности.
4.
0
0
)x(T
)x(Q)x(P
lim
ax
−
→
или
)x(Q)x(P
)x(T
lim
ax
−
→
,
где
)(xP
,
)(xQ
,
)(xT
– много-
члены
Числить и знаменатель дроби
умножить на
)()( xQxP + , затем
следовать алгоритму п. 3.

13
5.
0
0
)x(T
)x(Q)x(P
lim
ax
33
−
→
или
33
)x(Q)x(P
)x(T
lim
ax
−
→
,
где
)(xP , )(xQ , )(xT – много-
члены
Числить и знаменатель дроби
умножить на
2
33
2
3
))(()()())(( xQxQxPxP ++ ,
затем следовать алгоритму п. 3.
6.
∞−∞
)x(T
)x(S
)x(Q
)x(P
lim
)ax
(
x
−
→
∞→
или
,
где
)(xP , )(xQ , )(xS , )(xT –
многочлены
Привести дроби к общему зна-
менателю, затем см. п.1 или п. 3.
7.
∞−∞
))x(Q)x(P(lim
x
−
±∞→
,
где
)(xP , )(xQ – многочлены
Умножить и разделить выраже-
ние на
)()( xQxP + .
8.
∞−∞
))x(Q)x(P(lim
x
33
−
±∞→
,
где
)(xP
,
)(xQ
– многочлены
Умножить и разделить выраже-
ние на
2
33
2
3
))(()()())(( xQxQxPxP ++
.
9.
∞
1
)x(g
x
))x(f(lim +
→
1
0
,
где
0
0
=
→
)x(flim
x
,
∞
=
→
)x(glim
x 0
Представить выражение в виде
)()(
)(
1
]))(1[(
xgxf
xf
xf
⋅
+
.
По (5) e))x(f(lim
)x(f
x
=+
→
1
0
1 ,
найти
)x(g)x(flim
x
⋅
→0
.
10
.
∞⋅0
)x(g)x(flim
ax
⋅
→
,
где
0=
→
)x(flim
ax
,
∞
=
→
)x(glim
ax
Представить
)()( xgxf ⋅ в виде
)(
1
)(
xg
xf
(т.е.
0
0
) или
)(
1
)(
xf
xg
(т.е.
∞
∞
).
Применить правило Лопиталя:
(x)ψ
(x)
lim
ψ(x)
(x)
lim
axax
′
′
=
→→
ϕ
ϕ
.
11
.
∞
1 ,
0
0 ,
0
∞
)x(g
ax
)]x(f[lim
→
Представить
)x(g
)]x(f[ в виде
)x(fln)x(g
e
⋅
.
Найти
)x(fln)x(glim
ax
⋅
→
, исполь-
зуя правило Лопиталя.

14
3.7.Эквивалентные бесконечно малые
Определение. Бесконечно малые
)(x
α
и )(x
β
( 0=
→
)x(lim
ax
α
, 0
=
→
)x(lim
ax
β
)
называются эквивалентными бесконечно малыми при
a
x
→ , если
1
)(
)(
lim =
→
x
x
ax
β
α
(обозначение: )(x
α
~ )(x
β
).
Теорема: Если две пары бесконечно малых при
a
x
→ величин )(x
α
и
)(
~
x
α
,
)(x
β
и
)(
~
x
β
таковы, что
)(x
α
~
)(
~
x
α
,
)(x
β
~
)(
~
x
β
, то
)x(
~
)x(
~
lim
)x(
)x(
lim
axax
β
α
β
α
→→
= .
Таблица эквивалентных бесконечно малых
При
0→x
x
sin ~
x
;
x
tg ~
x
;
x
arcsin
~
x
;
x
arctg ~
x
;
)xln( +1
~
x
;
)x(log
a
+
1 ~
aln
x
;
)1( −
x
e ~
x
;
)1( −
x
a ~ alnx
⋅
;
)1)1(( −+
α
x ~
x
α
,...)3,2,1(
≠
α
.
3.8. Непрерывность и классификация точек разрыва
Определение: Если
)a(f)x(flim
ax
=
→
, то функция )x(fy
=
называется не-
прерывной в точке
a .
Теорема: Для того чтобы функция
)x(fy
=
была непрерывной в точке
a необходимо и достаточно, чтобы выполнялись условия:
1)
)x(fy =
определена в точке a и в некотором интервале, содержащем a ;
2)
)x(flim)x(flim
axax +→−→
=
;
3)
)a(f)x(flim)x(flim
axax
==
+→−→
.
Определение: Если хотя бы одно из условий 1)-3) не выполнено, то го-
ворят, что функция
)(xfy = в точке a терпит разрыв.
Классификация точек разрыва
Точки разрыва
I рода II рода
)x(flim),x(flim
axax +→−→
существуют и конечны
)x(flim
ax −→
или )x(flim
ax +→
не существуют или бесконеч-
ны (один из них или оба)
Устранимый разрыв
I рода
Неустранимый
разрыв II рода
)a(f)x(flim)x(flim
axax
≠
=
+→−→
)x(flim)x(flim
axax +→−→
≠

15
4. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ
ОДНОЙ ПЕРЕМЕННОЙ
4.1. Определение. Производной функции )x(fy
=
в точке
0
x
называет-
ся предел отношения приращения функции в этой точке к приращению аргу-
мента при условии, что последнее стремится к нулю, то есть
x
y
lim)x(f
x
∆
∆
=
′
→∆ 0
0
,
где )x(f)x(fy,xxx
00
−=∆−=∆ .
Обозначения y
′
,
x
y
′
,
dx
dy
, )x(f
′
.
Геометрически число )x(f
0
′
представляет собой угловой коэффициент
касательной (тангенс угла наклона касательной) к графику функции )x(fy
=
в точке
0
x .
4.2. Правила нахождения производной
Если
c
– постоянная величина и функции )x(uu
=
и )x(vv =
имеют производные, то
1. 0=
′
c ;
2. uc)cu(
′
=
′
;
3.
vu)vu(
′
+
′
=
′
+
;
4. uvvu)vu(
⋅
′
+
⋅
′
=
′
⋅
;
5.
2
v
uvvu
v
u ⋅
′
−⋅
′
=
′
⎟
⎠
⎞
⎜
⎝
⎛
.
6. Если функции
)u(yy
=
и )x(uu
=
имеют производ-
ные, то
xux
uyy
′
⋅
′
=
′
.
4.3. Таблица производных
1.
1−
=
′
nn
nx)x( (
n
— постоянное число).
В частности,
1=
′
x ,
2
11
x
x
−=
′
⎟
⎠
⎞
⎜
⎝
⎛
,
(
)
x
x
2
1
=
′
.
2.
xcos)x(sin =
′
; 3.
xsin)x(cos
−
=
′
;
4.
x
cos
)xtg(
2
1
=
′
; 5.
x
sin
)xctg(
2
1
−=
′
;
6.
2
1
1
x
)x(arcsin
−
=
′
; 7.
2
1
1
x
)x(arccos
−
−=
′
;
8.
2
1
1
x
)xarctg(
+
=
′
; 9.
2
1
1
x
)xarcctg(
+
−=
′
;
10.
xx
e)e( =
′
; 11. alna)a(
xx
⋅=
′
;
12.
x
)x(ln
1
=
′
; 13.
alnx
)x(log
a
⋅
=
′
1
;
14. xch)xsh( =
′
; 15. xsh)xch(
=
′
;
16.
x
ch
)xth(
2
1
=
′
; 17.
x
sh
)xcth(
2
1
−=
′
.

16
4.4. Производная обратной функции
Дифференцируемая функция
)x(yy
=
)( bxa
<
<
с производной
0
≠
′
)x(y
имеет однозначную непрерывную обратную функцию )y(xx = , причем об-
ратная функция также дифференцируема и справедлива формула
x
y
y
x
′
=
′
1
.
4.5. Производная функции, заданной параметрически
Система уравнений
⎩
⎨
⎧
=
=
),t(yy
),t(xx
)t(
β
α
<
<
,
где )t(x и )t(y – дифференцируемые функции и 0≠
′
)t(x , определяет y в
некоторой области, как однозначную дифференцируемую функцию от
x
,
причем производные этой функции могут быть найдены по формулам
t
t
x
x
y
y
′
′
=
′
,
3
)x(
yxyx
y
t
tttttt
xx
′
′
′
′
−
′
′
′
=
′′
.
4.6. Производная функции, заданной в неявном виде
Если дифференцируемая функция
)x(yy
=
удовлетворяет уравнению
0
=
)y,x(F ,
то производная )x(y
′
этой неявной функции может быть найдена из уравне-
ния
0=)]y,x(F[
dx
d
,
)x(y
′′
найдем из уравнения
0
2
2
=)]y,x(F[
dx
d
.
При нахождении производной считать
x
независимой переменной,
)x(y
–
функцией переменной
x
.
4.7. Уравнения касательной и нормали
Уравнение касательной к графику дифференцируемой функции
)x(fy = в точке ))x(f,x(M
00
)xx()x(f)x(fy
000
−
⋅
′
=
−
.
Уравнение нормали к графику дифференцируемой функции
)x(fy =
в
точке ))x(f,x(M
00
)xx(
)x(f
)x(fy
0
0
0
1
−
′
−=−
.
4.8. Дифференциал функции
Определение. Если приращение функции )x(fy
=
может быть пред-
ставлено в виде
)x(ox)x(Ay
∆
+
∆
=
∆
,

17
то линейная часть этого приращения x)x(A
∆
называется дифференциалом
функции )x(fy = . Обозначение x)x(Ady
∆
=
.
Для существования дифференциала функции )x(fy
=
необходимо и
достаточно, чтобы существовала конечная производная )x(f
′
, причем
dx)x(fdy
′
=
, где xdx
∆
=
.
Для приближенных вычислений используют формулу
dyy ≈∆
или )xx()x(f)x(f)x(f
000
−
⋅
′
+
≈
.
4.9. Формула Тейлора
Функция )x(fy
=
, дифференцируемая
1
+
n
раз в некотором интервале,
содержащем точку a , может быть представлена в виде
n
n
)n(
R)ax(
!n
)a(f
...)ax(
!
)a(f
)ax(
!
)a(f
)a(f)x(f +−++−
′′
+−
′
+=
2
21
,
где
1
1
1
+
+
−
+
−+
=
n
)n(
n
)ax(
)!n(
))ax(a(f
R
θ
, 10
<
<
θ
.
Частный вид формулы Тейлора при 0
=
a принято называть формулой
Маклорена.
4.10. Исследование функций
Определения Теоремы
Функция называется возрас-
тающей (убывающей) на ин-
тервале
(a,b), если
) f(x)f(x
21
< при bxxa <<
<
21
(или, соответственно,
) f(x)f(x
21
> при bxxa <<<
21
)
Достаточные условия возрастания и убы-
вания. Пусть функция
)x(fy
=
непрерывна
на
(a,b)
. Если при
);(x ba
∈
0
0
>
′
)x(f ,
то функция возрастает,
если
0)(
0
<
′
xf , то функция убывает на (a,b).
Функция )x(fy = имеет в
точке
0
x экстремум (макси-
мум или минимум),
если она определена в ин-
тервале
δ)x,-δ(x +
00
и для всех
δ)x,-δ(xx +∈
00
выполнено,
соответственно, неравенство
)f(xf(x)
0
< или )f(xf(x)
0
> .
Необходимые условия экстремума. Пусть
0
x – точка экстремума функции
)x(fy =
,
тогда
)(
0
xf
′
равна 0 или не существует.
Достаточные условия.
Теорема 1. Если 1) функция
)x(fy = опреде-
лена и непрерывна в некоторой окрестно-
сти
δ)x,-δ(x
+
00
точки
0
x такой, что )(
0
xf
′
равна
0 или не существует,
2)
)x(fy
=
имеет конечную производную
(x)f
′
на множестве δ),x(x)x,-(x +∪
0000
δ
,
3) производная имеет разные знаки на про-
межутках
)x,-δ(x
00
и δ),x(x
+
00
,
то
0
x – точка экстремума.

18
Теорема 2. Если функция
)x(fy =
имеет вто-
рую производную
(x)f
′
′
, в некоторой точке
0
x
выполнены условия
0
0
=
′
)(xf и 0
0
≠
′
′
)(xf ,
то в этой точке функция
)x(fy =
имеет экс-
тремум, а именно: максимум, когда
0
0
<
′
′
)(xf
,
минимум, когда 0
0
>
′
′
)(xf .
Теорема 3. Пусть функция
)x(fy = имеет в
некотором интервале
δ)x,-δ(x +
00
производные
(x)f
′
,…, (x)f
)(n-1
и в точке
0
x
производную
)(xf
(n)
0
, причем
0
0
=
′
)(xf , 0
0
=
′
′
)(xf ,…, 0
0
1
=)(xf
)(n-
, 0
0
≠)(xf
(n)
.
В таком случае,
1) если
n – четное число, то в точке
0
x
функ-
ция
f(x)y
=
имеет экстремум, а именно:
максимум при
0
0
<)(xf
(n)
, и минимум при
0
0
>)(xf
(n)
;
2) если
n - число нечетное, то в точке
0
x
функция
f(x)y
=
экстремума не имеет.
Если в некоторой окрестно-
сти точки
0
x кривая распо-
ложена ниже любой своей
касательной, то кривая на-
зывается выпуклой в точке
0
x . Если кривая расположе-
на выше любой своей каса-
тельной, то она называется
вогнутой в точке
0
x .
Достаточные условия вогнутости и вы-
пуклости. Если функция
)x(fy = дважды
дифференцируема на
(a,b) и 0
0
>
′′
)(xf для
всех
)(a;bx
∈
, то график функции на этом ин-
тервале вогнутый. Если
0
0
<
′′
)(xf для всех
)(a;bx
∈
, то график на этом интервале выпук-
лый.
Точки, в которых меняется
направление вогнутости
графика функции, называ-
ются точками перегиба.
Достаточное условие точки перегиба. Точ-
ка
0
x , для которой 0
0
=
′
′
)(xf или )(xf
0
′′
не су-
ществует, причем
)(xf
0
′
определена, есть
точка перегиба, если
(x)f
′
′
меняет свой знак
при переходе через
0
x .
4.11. Асимптоты
Определение. Если расстояние от точки
)y,x(M кривой f(x)y = до не-
которой прямой
L при неограниченном удалении точки
M
от начала коор-
динат стремится к нулю, то эта прямая называется асимптотой кривой
f(x)y = .
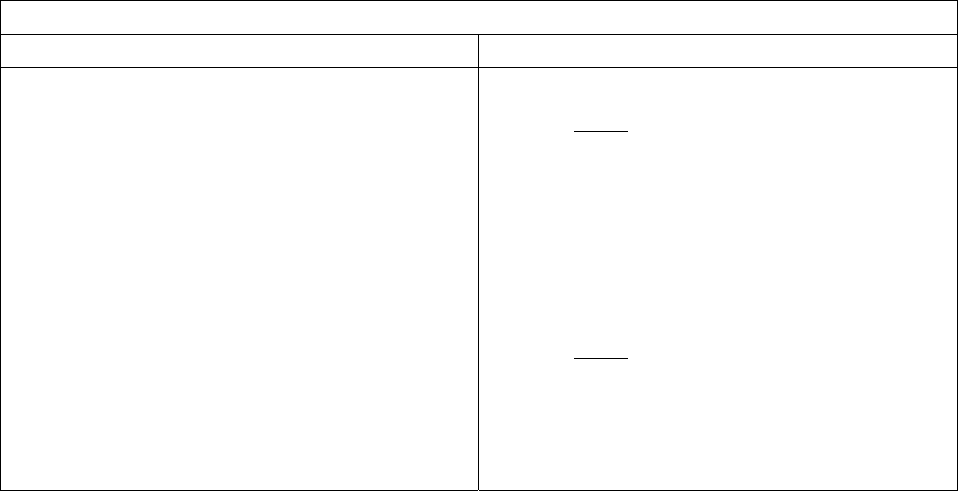
19
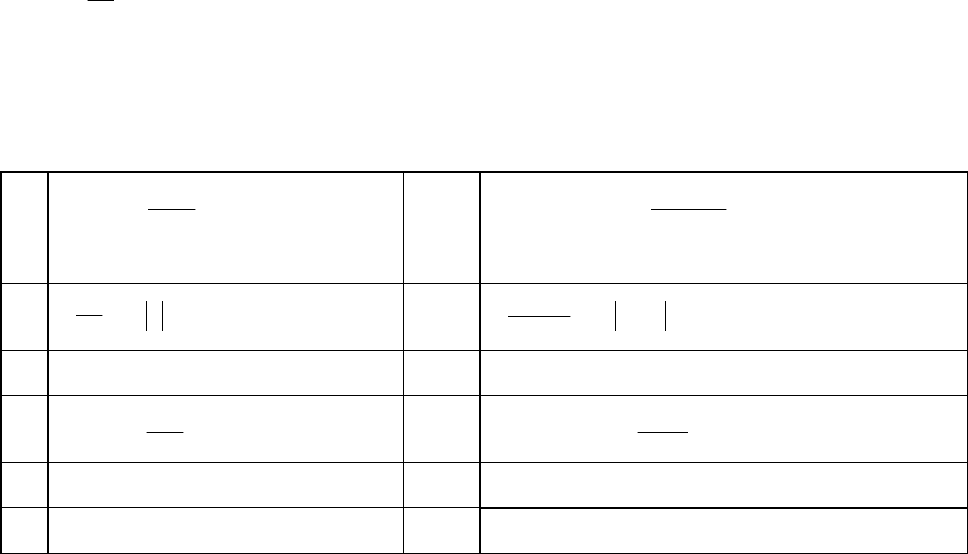
Асимптоты
Вертикальные Наклонные и горизонтальные
Если выполняется хотя бы одно из
условий
∞=
+→
)x(flim
ax 0
или
∞
=
−→
)x(flim
ax 0
,
то прямая
a
x
=
является вертикаль-
ной асимптотой графика функции
f(x)y = .
Если существуют конечные пределы
x
)x(f
limk
x +∞→
= и
),kx)x(f(limb
x
−
=
+∞→
то
прямая
bkxy
+
=
является правой на-
клонной, а при
0
=
k
правой горизон-
тальной асимптотой.
Если существуют конечные
пределы
x
)x(f
limk
x −∞→
= и ),kx)x(f(limb
x
−
=
−∞→
то прямая
bkxy
+
=
является левой
наклонной, а при
0=k левой гори-
зонтальной асимптотой.
4.12. Схема исследования функции
1. Найти область определения функции, область её непрерывности и точки
разрыва. Вычислить значение функции или соответствующие пределы в
граничных точках.
2. Найти асимптоты.
3. Выяснить, является ли функция четной, нечетной, сделать вывод о сим-
метрии её графика. Исследовать функцию на периодичность.
4. Определить точки пересечения графика функции
с осями координат,
промежутки знакопостоянства функции.
5. Определить экстремумы и интервалы возрастания и убывания функции (с
помощью первой производной).
6. Определить интервалы выпуклости, вогнутости и точки перегиба графика
функции (с помощью второй производной).
7. Построить график функции.
8. Найти множество значений функции.
4.13. Нахождение наибольшего и наименьшего значений функции
на
отрезке.
Теорема Вейерштрасса. Функция непрерывная на отрезке
[a,b] обяза-
тельно имеет на этом отрезке наибольшее и наименьшее значения.
Эти значения достигаются функцией или в точках экстремума, лежа-
щих внутри отрезка, или на концах этого отрезка.
Алгоритм нахождения наибольшего и наименьшего значений функции
на отрезке.
1. Найти критические точки, где производная функции равна нулю или не
существует, лежащие внутри
отрезка [a,b] .
2. Вычислить значения функции в этих критических точках и на концах от-
резка.
3. Сравнить полученные значения функции. Выбрать из них наибольшее и
наименьшее.
20
5. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ
ОДНОЙ ПЕРЕМЕННОЙ
5.1. Первообразная функция и неопределенный интеграл
Отыскание функции
)x(F по известному её дифференциалу
dx)x(f)x(dF =
[или по известной производной
)x(f)x('F
=
], т.е. действие об-
ратное дифференцированию, называется интегрированием, а искомая функ-
ция
)x(F называется первообразной функции )x(f .
Если
)x(F
есть первообразная функции
)x(f
, т.е. если
)x(f)x('F =
, то
и
C)x(F + , где C – произвольная постоянная, есть также первообразная
функции
)(xf , так как )x(f)x('F)'C)x(F(
=
=
+ .
Общее выражение
C)x(F
+
совокупности всех первообразных функ-
ции
)x(f
называют неопределенным интегралом от этой функции и обозна-
чают
∫
+= C)x(Fdx)x(f
.
5.2.Свойства неопределенного интеграла
I. Постоянный множитель можно выносить за знак интеграла
∫
∫
= dx)x(fadx)x(af .
II. Интеграл суммы равен сумме интегралов слагаемых
∫
∫
∫
+=+ dx)x(fdx)x(fdx)]x(f)x(f[
2121
.
III.
)x(f]dx)x(f[
dx
d
=
∫
или
dx)x(fdx)x(fd =
∫
.
IV.
∫
+= C)x(Fdx)x('F или
∫
+= C)x(F)x(dF .
5.3.Основные формулы интегрирования.
1.
∫
−≠+
+
=
+
1 ,
1
1
nC
n
x
dxx
n
n
.
В частности,
∫
+= Cxdx
1.*
∫
−≠+
+
=
+
1
1
1
n,C
n
)x(u
)x(du)x(u
n
n
.
В частности,
∫
+= Cxuxdu )()(
2.
∫
+= Cxln
x
dx
2.*
∫
+= C)x(uln
)x(u
)x(du
3.
∫
+= Cedxe
xx
3.*
∫
+= Cexdue
xuxu )()(
)(
4.
∫
+= C
aln
a
dxa
x
x
4.*
∫
+= C
aln
a
)x(dua
)x(u
)x(u
5.
∫
+−= Cxcosxdxsin
5.*
∫
+−= C)x(ucos)x(du)x(usin
6.
∫
+= Cxsinxdxcos
6.*
∫
+= C)x(usin)x(du)x(ucos
