Шпоры по гидравлике
Подождите немного. Документ загружается.

17. Ламинарное движение
Это движение, называют также потенциальным (безE
вихревым) движением.
При таком движении отсутствует вращение частиц
вокруг мгновенных осей, которые проходят через поE
люсы жидких частиц. По этой причине:
υ
x
= 0; υ
y
= 0; υ
z
= 0. (1)
ω
x
= ω
y
= ω
z
= 0.
Выше отмечалось, что при движении жидкости проE
исходит не только изменение положения частиц в простE
ранстве, но и их деформация по линейным параметE
рам. Если рассмотренное выше вихревое движение
является следствием изменения пространственноE
го положения жидкой частицы, то ламинарное (по&
тенциальное, или безвихревое) движение являетE
ся следствием деформационных явлений линейных
параметров, например, формы и объема.
Вихревое движение определялось направлением
вихревого вектора
где υ — угловая скорость, которая является характеE
ристикой угловых деформаций.
Деформацию этого движения характеризируют деE
формацией этих компонентов
;;. (3)
y
xz
xyz
I
II
υ
υυ
υυυ
2, (2)=
θυ
G
G
17а
11
19. Уравнение неразрывности
жидкости
Довольно часто при решении задач приходится опреE
делять неизвестные функции типа:
1) р = р (х, у, z, t) — давление;
2) n
x
(х, у, z, t), n
y
(х, у, z, t), n
z
(х, у, z, t) — проекции скоE
рости на оси координат х, у, z;
3) ρ (х, у, z, t) — плотность жидкости.
Эти неизвестные, всего их пять, определяют по
системе уравнений Эйлера.
Количество уравнений Эйлера всего три, а неизвестE
ных, как видим, пять. Не хватает еще двух уравнений
для того, чтобы определить эти неизвестные. УравнеE
ние неразрывности является одним из двух недостаюE
щих уравнений. В качестве пятого уравнения испольE
зуют уравнение состояния сплошной среды.
Формула (1) является уравнением неразрывности,
то есть искомое уравнение для общего случая. В слуE
чае несжимаемости жидкости ∂ρ/dt = 0, поскольку ρ =
= const, поэтому из (1) следует:
поскольку эти слагаемые, как известно из курса высE
шей математики, являются скоростью изменения длиE
ны единичного вектора по одному из направлений
X, Y, Z.
0, (2)
Ux Uy Uz
xyz
∂∂∂
++=
∂∂∂
0. (1)
Ux Uy Uz
txyz
ρ
ρ
∂∂∂∂
⎛⎞
−++=
⎜⎟
∂∂∂∂
⎝⎠
20. Характеристики потока жидкости
В гидравлике потоком считают такое движение масE
сы, когда эта масса ограничена:
1) твердыми поверхностями;
2) поверхностями, которые разделяют разные жидE
кости;
3) свободными поверхностями.
В зависимости от того, какого рода поверхностями
или их сочетаниями ограничена движущаяся жидE
кость, различают следующие виды потоков:
1) безнапорные, когда поток ограничен сочетанием
твердой и свободной поверхностей, например, реE
ка, канал, труба с неполным сечением;
2) напорные, например, труба с полным сечением;
3) гидравлические струи, которые ограничены жидE
кой (как мы увидим позже, такие струйки называют
затопленными) или газовой средой.
Живое сечение и гидравлический радиус пото&
ка. Уравнение неразрывности в гидравлической
форме
Сечение потока, с которого все линии тока нормальE
ны (т. е. перпендикулярны), называется живым сече&
нием.
Чрезвычайно важное значение имеет в гидравлике
понятие о гидравлическом радиусе
Для напорного потока с круглым живым сечением,
диаметром d и радиусом r
0
, гидравлический радиус
выражается
2
(2)
44
dd
R.
d
ωπ
χπ
== =
(1)R.
ω
χ
=
18. Потенциал скорости и ускорение
при ламинарном движении
ϕ = ϕ(x, y, z) (1)
Функция ϕ называется потенциалом скорости.
С учетом этого, компоненты ϕ выглядят следующим
образом:
Формулой (1) описывается неустановившееся двиE
жение,поскольку она содержит параметр t.
Ускорение при ламинарном движении
Ускорение движения жидкой частицы имеет вид:
где du/dt — полные производные по времени.
Ускорение можно представить в таком виде, исходя
из Составляющие искомого ускоE
рения
,
,(4)
.
xx x x xz
x
yy y y yz
x
zz z z zz
x
du u u u u u
=+i+iy+
dt t x y z
du u u u u u
=+i+iy+
dt t x y z
du u u u u u
=+i+iy+
dt t x y z
υυ υ υ
υυ υ υ
υυ υ υ
υυ υ υ
υυ υ υ
υυ υ υ
⎧⎫
⎨⎬
⎩⎭
⎧⎫
⎪⎪
⎨⎬
⎪⎪
⎩⎭
⎧⎫
⎨⎬
⎩⎭
.
dy dz
=iy; =iz
dt dt
;
dx
=ix
dt
,(3)
du u i du i du i du
=+ + +
dt t x dt y dt z dz
υυ υ υ
υυ υ υ
×××
;;. (2)
yyz
I= I= I=
xyz
υϕ υϕ υϕ
υυυ
−−−
18а
19а
20а
Но, поскольку при ламинарном движении υ
x
=
= υ
y
= υ
z
= 0, то:
Из этой формулы видно: поскольку существуют частE
ные производные, связанные между собой в формуле
(4), то эти частные производные принадлежат некотоE
рой функции.
,
,(4)
.
y
x
xz
y
z
u
dh
=
dy x
Iu
=
zx
I
u
=
zy
υ
υ
υυ
υυ
υ
υ
υυ
17б
12
Формула (4) содержит в себе информацию о полE
ном ускорении.
Слагаемые υu
x
/υt, υu
y
/υt, υu
z
/υt, называют местными
ускорителями в рассматриваемой точке, которыми хаE
рактеризуются законы изменения поля скоростей.
Если движение установившееся, то
Само поле скоростей может быть названо конвекци&
ей. Поэтому остальные части сумм, соответствующие
каждой строке (4), называют конвективными ускоре&
ниями. Точнее, проекциями конвективного ускорения,
которое характеризует неоднородность поля скоростей
(или конвекций) в конкретный момент времени t.
Само полное ускорение можно назвать некоторой
субстанцией, которая является суммой проекций
du
x
/dt, du
y
/dt, du
z
/dt,
0.
y
xz
u
uu
===
ttt
υ
υυ
υυυ
При выводе (2) учли
Расход потока — это такое количество жидкости,
которое проходит через живое сечение за единицу вреE
мени.
Для потока, состоящего из элементарных струек,
расход:
где dQ = dω — расход элементарного потока;
U — скорость жидкости в данном сечении.
Q = uw.
,(4)QdQ Ud
ωω
ω
==
∫∫
2
2
0
;. (3)
24
r
d
xd
π
ωπ π
⎛⎞
== =
⎜⎟
⎝⎠
Что касается всей суммы в (2), то она выражает
скорость относительного изменения объема dV.
Это объемное изменение называют поEразному: объеE
мным расширением, дивергенцией, расхождением векE
тора скоростей.
Для струйки уравнение будет иметь вид:
где Q — количество жидкости (расход);
ω — угловая скорость струйки;
∂l — длина элементарного участка рассматриE
ваемой струйки.
Если давление установившееся или площадь живоE
го сечения ω = const, то ∂ω /∂t = 0, т. е. согласно (3),
ρ∂Q/∂l = 0, следовательно,
0. (4)
Q
l
∂
=
∂
() ()
0, (3)
Qv
lt
ρρω
∂
+=
∂∂
18б
19б
20б
24. Форма Громеки
уравнения движения
невязкой жидкости
Уравнения Громеки — попросту другая, несколько
преобразованная форма записи уравнения Эйлера.
Например, для координаты x.
Чтобы его преобразовать, используют уравнения комE
понентов угловой скорости для вихревого движения.
Преобразовав точно так же yEвую и zEвую компоненE
ту, окончательно приходим к форме Громеко уравнеE
ния Эйлера:
Уравнение Эйлера было получено российским учеE
ным Л. Эйлером в 1755 г., и преобразовано в вид (2)
опять же российским ученым И. С. Громекой в 1881 г.
2
2
2
1
2( )
2
1
2( ) . (2)
2
1
2( )
2
yz
zx
xy
Ux U
Fx Uz Uy
xdt x
Uy U
Fy Ux Uz
xdt y
Uz U
Fz Uy Ux
xdt z
ωω
ωω
ωω
ρ
ρ
ρ
ρ
ρ
ρ
⎧
∂∂ ∂
−× = + × + −
⎪
∂∂
⎪
⎪
∂∂ ∂
⎪
−× = + × + −
⎨
∂∂
⎪
⎪
∂∂ ∂
⎪
−× = + × + −
∂∂
⎪
⎩
1
.(1)
Ux Ux Ux Ux
Fx Ux Uy Uz
xdt x y z
ρ
ρ
∂∂ ∂ ∂ ∂
−× = + + +
∂∂∂∂
13
21. Разновидность движения
В зависимости от характера изменения поля скоE
ростей различают следующие виды установившегося
движения:
1) равномерное, когда основные характеристики поE
тока — форма и площадь живого сечения, средняя
скорость потока, в том числе по длине, глубине
потока (если движение безнапорное), — постоянE
ны, не изменяются; кроме того, по всей длине поE
тока вдоль линии тока местные скорости одинакоE
вы, а ускорений вовсе нет;
2) неравномерное, когда ни один из перечисленных
для равномерного движения факторов не выполE
няется, в том числе и условие параллельности лиE
ний токов.
Существует плавно изменяющееся движение, коE
торое все же считают неравномерным движением;
при таком движении предполагают, что линии тока
примерно параллельны, и все остальные изменеE
ния происходят плавно. Поэтому, когда направлеE
ние движения и ось ОХ сонаправлены, то пренебреE
гают некоторыми величинами
Ux ≈ U; Uy = Uz = 0. (1)
Уравнение неразрывности (1) для плавно изменяюE
щегося движения имеет вид:
аналогично для остальных направлений.
Поэтому такого рода движение называют равномерE
ным прямолинейным;
0, (2)
U
x
∂
=
∂
23. Уравнение Эйлера
для разных состояний
Уравнение Эйлера для разных состояний имеет разE
ные формы записи. Поскольку само уравнение полуE
чено для общего случая, то рассмотрим несколько слуE
чаев:
1) движение неустановившееся.
2) жидкость в покое. Следовательно, Ux = Uy = Uz = 0.
В таком случае уравнение Эйлера превращается
в уравнение равномерной жидкости. Это уравнеE
ние также дифференциальное и является системой
из трех уравнений;
3) жидкость невязкая. Для такой жидкости уравнеE
ние движения имеет вид:
где Fl — проекция плотности распределения сил
массы на направление, по которому направлена
касательная к линии тока;
dU/dt — ускорение частицы.
1
,
dU
Fl
ldt
ρ
ρ
∂
−× =
∂
1
1
;
1
Ux Ux Ux Ux
Fx Ux Uy Uz
xdt x y z
Uy Uy Uy Uy
Fy Ux Uy Uz
xdt x y z
Uz Uz Uz Uz
Fz Ux Uy Uz
xdt x y z
ρ
ρ
ρ
ρ
ρ
ρ
⎧∂∂∂∂∂
−× = + + +
⎪
∂∂∂∂
⎪
⎪
∂∂∂∂∂
⎪
−×=+++
⎨
∂∂∂∂
⎪
⎪
∂∂ ∂ ∂ ∂
−× = + + +
⎪
∂∂∂∂
⎪
⎩
22. Дифференциальные уравнения
движения невязкой
жидкости
Уравнение Эйлера служит одним из фундаментальE
ных в гидравлике, наряду с уравнением Бернулли и неE
которыми другими.
Изучение гидравлики как таковой практически наE
чинается с уравнения Эйлера, которое служит исходE
ным пунктом для выхода на другие выражения.
Попробуем вывести это уравнение. Пусть имеем
бесконечно малый параллелепипед с гранями dxdydz
в невязкой жидкости с плотностью ρ. Он заполнен
жидкостью и движется как составная часть потока. КаE
кие силы действуют на выделенный объект? Это силы
массы и силы поверхностных давлений, которые дейE
ствуют на dV = dxdydz со стороны жидкости, в которой
находится выделенный dV. Как силы массы пропорE
циональны массе, так и поверхностные силы пропорE
циональны площадям, на которые оказывается даE
вление. Эти силы направлены к граням вовнутрь по
нормали. Определим математическое выражение
этих сил.
Назовем, как и при получении уравнения неразрывE
ности, грани параллелепипеда:
1, 2 — перпендикулярные к оси О
Х
и параллельные
оси О
Y
;
3, 4 — перпендикулярные к оси O
Y
и параллельные
оси О
Х
;
5, 6 — перпендикулярные к оси O
Z
и параллельные
оси О
Х
.
Теперь нужно определить, какая сила приложена
к центру масс параллелепипеда.
21а
22а
23а
24а

14
Сила, приложенная к центру массы параллелеE
пипеда, которая и заставляет эту жидкость соE
вершать движение, есть сумма найденных сил, то есть
Получили уравнение движения параллелепипеда
с dV
1
по направлению оси Х.
Делим (1) на массу ρdxdydz:
Полученная система уравнений (2) есть искомое уравE
нение движения невязкой жидкости — уравнение
Эйлера.
К трем уравнениям (2) добавляются еще два уравнеE
ния, поскольку неизвестных пять, и решается система
из пяти уравнений с пятью неизвестными: одним из
двух дополнительных уравнений является уравнение
неразрывности. Еще одним уравнением является
уравнение состояния. Например, для несжимаемой
жидкости уравнением состояния может быть условие
ρ = const.
Уравнение состояния должно быть выбрано таким
образом, чтобы оно содержало хотя бы одно из пяти
неизвестных.
1
1
.(2)
1
dUx
Fx
xdt
dUy
Fy
ydt
dUz
Fz
zdt
ρ
ρ
ρ
ρ
ρ
ρ
⎧∂
−× =
⎪
∂
⎪
⎪
∂
⎪
−× =
⎨
∂
⎪
⎪
∂
−× =
⎪
∂
⎪
⎩
.(1)
dUx
Fx dxdydz dxdydz dxdydz
xdt
ρ
ρρ
∂
−=
∂
Уравнение Громеко (под воздействием массоE
вых сил на жидкость):
Поскольку
–dП = Fxdx + Fydy + Fzdz, (4)
то для компонентов Fy, Fz можно вывести те же выраE
жения, что и для Fx, и, подставив это в (2), прийти к (3).
2
2
2
2( )
2
2( ) . (3)
2
2( )
2
yz
zx
y
pU Ux
ПUzUy
xdt
pU Uy
ПUxUz
ydt
pU Uz
ПUyxUx
zdt
ωω
ωω
ωω
ρ
ρ
ρ
⎧
⎛⎞
∂∂
−− − = + −
⎜⎟⎪
∂
⎝⎠
⎪
⎪
⎛⎞
∂∂
⎪
−− − = + −
⎜⎟
⎨
∂
⎝⎠
⎪
⎪
⎛⎞
∂∂
⎪
−− − = + −
⎜⎟
⎪
∂
⎝⎠
⎩
Подставив U = dl/dt в (2) и учтя, что (∂U/∂l)U =
= 1/2(∂U
2
/∂l ), получим уравнение.
Мы привели три формы уравнения Эйлера для трех
частных случаев. Но это не предел. Главное — праE
вильно определить уравнение состояния, которое соE
держало хотя бы один неизвестный параметр.
Уравнение Эйлера в сочетании с уравнением неразE
рывности может быть применено для любого случая.
Уравнение состояния в общем виде:
Таким образом, для решения многих гидродинамиE
ческих задач оказывается достаточно уравнения ЭйлеE
ра, уравнения неразрывности и уравнения состояния.
С помощью пяти уравнений легко находятся пять
неизвестных: p, Ux, Uy, Uz, ρ.
Невязкую жидкость можно описать и другим уравнеE
нием.
0. (3)
Ux Uy Uy
xyz
∂∂∂
++=
∂∂∂
3) если движение нестационарное или неустаноE
вившееся, когда местные скорости с течением
времени изменяются, то в таком движении разлиE
чают следующие разновидности: быстро изме&
няющееся движение, медленно изменяющееся
движение, или, как часто его называют, квазиста&
ционарное.
Давление разделяют в зависимости от количества
координат в описывающих его уравнениях, на: простE
ранственное, когда движение трехмерное; плоское,
когда движение двухмерное, т. е. Uх, Uy или Uz равна
нулю; одномерное, когда движение зависит только от
одной из координат.
В заключение отметим следующее уравнение неE
разрывности для струйки, при условии, что жидкость
несжимаемая, т. е. ρ = const, для потока это уравнение
имеет вид:
Q = υ
1
ω
1
= υ
2
ω
2
= … = υ
i
ω
i
= idem, (3)
где υ
i
ω
i
— скорость и площадь одного и того же сечеE
ния с номером i.
Уравнение (3) называют уравнением неразрывно&
сти в гидравлической форме.
21б
22б
23б
24б

15
25. Уравнение Бернулли
Уравнение Громеки подходит для описания движеE
ния жидкости, если компоненты функции движения
содержат какуюEто вихревую величину. Например, эта
вихревая величина содержится в компонентах ω
x
, ω
y
,
ω
z
угловой скорости w.
Условием того, что движение является установивE
шимся, является отсутствие ускорения, то есть услоE
вие равенства нулю частных производных от всех комE
понентов скорости:
Если теперь сложить то получим
что и есть равенство ускорения. Условием неE
вязкой несжимаемой жидкости является:
1) отсутствие трения (внутри жидкости);
2) постоянство (однородности) плотности ρ = const.
С учетом (1), следует:
2
2
2
2( )
2
2( ) . (2)
2
2( )
2
yz
zx
xy
pU
ПUzUy
dx
pU
ПUxUz
dy
pU
ПUyUx
dz
ωω
ωω
ωω
ρ
ρ
ρ
⎧
⎛⎞
∂
−− − = −
⎜⎟⎪
⎝⎠
⎪
⎪
⎛⎞
∂
⎪
−− − = −
⎜⎟
⎨
⎝⎠
⎪
⎪
⎛⎞
∂
⎪
−− − = −
⎜⎟
⎪
⎝⎠
⎩
0,
Ux
dt
∂
=
,
Ux Uy Uz
dt dt dt
∂∂∂
++
0. (1)
Ux Uy Uz
dt dt dt
∂∂∂
===
27. Примеры прикладного
применения уравнения Бернулли
Во всех случаях требуется определить математичеE
скую формулу потенциальной функции, которая вхоE
дит в уравнение Бернулли: но эта функция имеет разE
ные формулы в разных ситуациях. Ее вид зависит от
того, какие массовые силы действуют на рассматриE
ваемую жидкость. Поэтому рассмотрим две ситуации.
Одна массовая сила
В этом случае подразумевается сила тяжести, котоE
рая выступает в качестве единственной массовой сиE
лы. Очевидно, что в этом случае ось Z и плотность
распределения Fz силы П противонаправлены, следоE
вательно,
Fx = Fy = 0; Fz = –g.
Поскольку –dП = Fxdx + Fydy + Fzdz, то –dП = Fzdz,
окончательно dП = –gdz.
Интегрируем полученное выражение:
П = –gz + C, (1)
где С — некоторая постоянная.
Подставив (1) в уравнение Бернулли, имеем выраE
жение для случая воздействия на жидкость только одE
ной массовой силы:
2
const. (2)
2
pU
gz
ρ
++ =
28. Случаи, когда массовых
сил несколько
В этом случае усложним задачу. Пусть на частицы
жидкости действуют следующие силы: сила тяжести;
центробежная сила инерции (переносит движение от
центра); кориолисовая сила инерции, которая заставE
ляет частицы вращаться вокруг оси Z с одновременE
ным поступательным движением.
В этом случае мы получили возможность предстаE
вить себе винтовое движение. Вращение происходит
с угловой скоростью w. Нужно представить себе криE
волинейный участок некоторого потока жидкости, на
этом участке поток как бы вращается вокруг некотоE
рой оси с угловой скоростью.
Частным случаем такого потока можно считать гидE
равлическую струю. Вот и рассмотрим элементарную
струйку жидкости и применим в отношении к ней ураE
внение Бернулли. Для этого поместим элементарную
гидравлическую струю в координатную систему XYZ
таким образом, чтобы плоскость YOX вращалась воE
круг оси O
Z
.
Будем считать, что — местная скорость жидкости
во вращающейся плоскости YOX. Пусть
Fx
1
= Fy
1
= 0; Fz
1
=–g —
составляющие силы тяжести (то есть ее проекции на
оси координат), отнесенные к единичной массе жидE
кости. К этой же массе приложена вторая сила — сила
инерции ω
2
r, где r — расстояние от частицы до оси
вращения ее компоненты.
Fx
2
= ω
2
x; Fy
2
= ω
2
y; Fz
2
= 0
изEза того, что ось O
Z
«не вращается».
U
JJG
26. Анализ уравнения Бернулли
это уравнение есть не что иное, как уравнение линии
тока при установившемся движении.
Отсюда следуют выводы:
1) если движение установившееся, то первая и третья
строки в уравнении Бернулли пропорциональны.
2) пропорциональны строки 1 и 2, т. е.
Уравнение (2) является уравнением вихревой лиE
нии. Выводы из (2) аналогичны выводам из (1),
только линии тока заменяют вихревые линии. ОдE
ним словом, в этом случае условие (2) выполняетE
ся для вихревых линий;
3) пропорциональны соответствующие члены строк
2 и 3, т. е.
где а — некоторая постоянная величина; если подE
ставить (3) в (2), то получим уравнение линий тока
(1), поскольку из (3) следует:
ω
x
= aUx; ω
y
= aUy; ω
z
= aUz. (4)
const , (3)
xyz
a
Ux Uy Uz
ωωω
=== =
.(2)
dx dy dz
xyz
ωωω
==
—(1)
dx dy dz
Ux Uy Uz
==
25а
26а
27а
28а
16
Здесь следует интересный вывод о том, что векE
торы линейной скорости и угловой скорости
сонаправлены, то есть параллельны.
В более широком понимании надо представить сеE
бе следующее: так как рассматриваемое движение
установившееся, то получается, что частицы жидE
кости движутся по спирали и их траектории по спиE
рали образуют линии тока. Следовательно, линии
тока и траектории частиц — одно и то же. ДвижеE
ние такого рода называют винтовым.
4) вторая строка определителя (точнее, члены второй
строки) равна нулю, т. е.
ω
x
= ω
y
= ω
z
= 0. (5)
Но отсутствие угловой скорости равносильно отE
сутствию вихревости движения.
5) пусть строка 3 равна нулю, т. е.
Ux = Uy = Uz = 0.
Но это, как нам уже известно, условие равновесия
жидкости.
Анализ уравнения Бернулли завершен.
ω
JG
U
JJG
Окончательно уравнение Бернулли. Для расE
сматриваемого случая:
Или, что одно и то же, после деления на g
Если рассмотреть два сечения элементарной струйE
ки, то, применив вышеуказанный механизм, легко убеE
диться, что
где z
1
, h
1
, U
1
, V
1
, z
2
, h
2
, U
2
, V
2
— параметры соответE
ствующих сечений.
222 2
22
11 1 2 2
122
,
22 2
pU r p U
gz gz r
gg g
ω
ω
ρρ
++ − = ++ −
222
const.
22
pU r
z
ggg
ω
ρ
++− =
222
const.
22
pU r
gz
ω
ρ
++ − =
Если разделить уравнение (2) на g (поскольку
оно постоянное), то
Мы получили одну из самых часто применяемых в реE
шении гидравлических задач формул, поэтому следует
ее запомнить особенно хорошо.
Если требуется определить расположение частицы
в двух разных положениях, то выполняется соотношеE
ние для координат Z
1
и Z
2
, характеризующие эти полоE
жения
Можно переписать (4) в другой форме:
22
12
.(5)
22
pU pU
ZZ
gg gg
ρρ
++=++
22
12
.(4)
22
pU pU
gZ gZ
ρρ
++ = ++
2
const. (3)
2
pU
z
gg
ρ
++=
Если проецировать перемещение на бесконечE
но малую величину dl на координатные оси, то
получим:
dx = Uxdt; dy = Uydt; dz = Uzdt. (3)
Теперь помножим каждое уравнение (3) соответE
ственно на dx, dy, dz, и сложим их:
Предположив, что правая часть равна нулю, а это
возможно, если вторая или третья строки равны нулю,
получим:
Нами получено уравнение Бернулли.
2
0. (5)
2
pU
dП
ρ
⎛⎞
++ =
⎜⎟
⎝⎠
2
2( ) . (4)
2
y
pU
ПdxUzUyzdx
x
ωω
ρ
⎛⎞
∂
−− + = −
⎜⎟
∂
⎝⎠
25б
26б
27б
28б
17
29. Энергетический смысл
уравнения Бернулли
Пусть теперь имеем установившееся движение жидE
кости, которая невязкая, несжимаемая.
И пусть она находится под воздействием сил тяжести
и давления, тогда уравнение Бернулли имеет вид:
Теперь требуется идентифицировать каждое из слаE
гаемых. Потенциальная энергия положения Z — это
высота элементарной струйки над горизонтальной
плоскостью сравнения. Жидкость с массой М на выE
соте Z от плоскости сравнения имеет некоторую поE
тенциальную энергию MgZ. Тогда
Это та же потенциальная энергия, отнесенная к едиE
ничной массе. Поэтому Z называют удельной потенE
циальной энергией положения.
Движущаяся частица с массой М и скоростью u имеE
ет вес MG и кинематическую энергию U
2
/2g. Если соE
отнести кинематическую энергию с единичной масE
сой, то
22
.
22
UU
M =
.
MgZ
Z
Mg
=
2
const.
2
U
p
z
gg
ρ
++=
31. Уравнения движения
вязкой жидкости
Для получения уравнения движения вязкой жидкости
рассмотрим такой же объем жидкости dV = dxdydz, коE
торый принадлежит вязкой жидкости (рис. 1).
Грани этого объема обозначим как 1, 2, 3, 4, 5, 6.
Рис. 1. Силы, действующие на элементарный
объем вязкой жидкости в потоке
Будем считать, что для любой точки жидкости
τ
xy
= τ
yx
; τ
xz
= τ
zx
; τ
yz
= τ
zy
. (1)
Тогда из шести касательных напряжений остается
только три, поскольку попарно они равны. Поэтому
для описания движения вязкой жидкости оказываютE
32. Деформация в движущейся
вязкой жидкости
В вязкой жидкости имеются силы трения, в силу этоE
го при движении один слой тормозит другой. В итоге
возникает сжатие, деформация жидкости. ИзEза этого
свойства жидкость и называют вязкой.
Если вспомнить из механики закон Гука, то по нему
напряжение, которое возникает в твердом теле, проE
порционально соответствующей относительной деE
формации. Для вязкой жидкости относительную деE
формацию заменяет скорость деформации. Речь
идет об угловой скорости деформации частицы жидE
кости dΘ/dt, которую поEдругому называют скороE
стью деформации сдвига. Еще Исааком Ньютоном
установлена закономерность о пропорциональности
силы внутреннего трения, площади соприкосновения
слоев и относительной скорости слоев. Также им был
установлен
коэффициент пропорциональности динамической вязE
кости жидкости.
Если выразить касательное напряжение через его
компоненты, то
,
,(2)
.
y
x
xy
zx
xz
z
yz
u
u
xy
uu
xz
u
z
y
τμ
τμ
τμ
⎧∂
⎛⎞
∂
=+
⎜⎟
⎪
⎜⎟
∂∂
⎪
⎝⎠
⎪
∂∂
⎛⎞
⎪
=+
⎨
⎜⎟
∂∂
⎝⎠
⎪
⎪
∂
⎛⎞
⎪
=+
⎜⎟
⎪
∂
⎝⎠
⎩
—(1)
dt
τμ
Θ
=
30. Геометрический смысл
уравнения Бернулли
Основу теоретической части такой интерпретации соE
ставляет гидравлическое понятие напор, которое приE
нято обозначать буквой Н, где
Гидродинамический напор Н состоит из следующих
разновидностей напоров, которые входят в формулу
(198) как слагаемые:
1) пьезометрический напор, если в (198) p = p
изг
, или
гидростатический, если p ≠ p
изг
;
2) U
2
/2g — скоростной напор.
Все слагаемые имеют линейную размерность, их
можно считать высотами. Назовем эти высоты:
1) z — геометрическая высота, или высота по положеE
нию;
2) p/ρg — высота, соответствующая давлению p;
3) U
2
/2g — скоростная высота, соответствующая скоE
рости.
Геометрическое место концов высоты Н соответствуE
ет некоторой горизонтальной линии, которую принято
называть напорной линией или линией удельной
энергии.
Точно так же (по аналогии) геометрические места
концов пьезометрического напора принято называть
пьезометрической линией. Напорная и пьезометри&
ческая линии расположены друг от друга на расстояE
нии (высоте) p
атм
/ρg, поскольку p = p
изг
+ p
ат
, т. е.
изг атм
.(2)
pp
p
gg g
ρρ ρ
=+
2
.(1)
2
pU
Hz
gg
ρ
=+ +
29а
30а
31а 32а
yz
yz
dy
y
τ
τ
∂
+
∂
zy
xy
dz
z
τ
τ
∂
+
∂
zz
zz
P
Pdz
z
∂
+
∂
zx
dz
z
τ
τ
∂
+
∂
yx
yx
dy
y
τ
τ
∂
+
∂
xz
xz
dx
x
τ
τ
∂
+
∂
xx
xx
P
Pdx
x
∂
+
∂
yy
yy
P
Pdy
y
∂
+
∂
xy
xy
dx
x
τ
τ
∂
+
∂
P
zz
X
Y
Z
C
HE
K
B
D
A
xx
P
1
G
3
O
5
yy
P

18
Отметим, что горизонтальная плоскость, содерE
жащая напорную линию и находящаяся над плоскоE
стью сравнения, называется напорной плоскостью. ХаE
рактеристику плоскости при разных движениях называют
пьезометрическим уклоном J
п
, который показывает,
как изменяется на единице длины пьезометрический наE
пор (или пьезометрическая линия):
Пьезометрический уклон считается положительным,
если он по течению струйки (или потока) уменьшается,
отсюда и знак минус в формуле (3) перед дифференE
циалом. Чтобы J
п
остался положительным, должно выE
полняться условие
0. (4)
dP
z
dl g
ρ
⎛⎞
+<
⎜⎟
⎝⎠
п
.(3)
dP
Jz
dl g
ρ
⎛⎞
=− +
⎜⎟
⎝⎠
А что касается нормальных напряжений (τ —
это касательная составляющая деформации),
которые зависимы от направления действия, то они
зависят также от того, к какой площади они приложеE
ны. Это их свойство называют инвариантностью.
Сумма значений нормальных напряжений
Чтобы окончательно установить зависимость между
pudΘ/dt через зависимость между нормальными (p
xx
,
p
yy
, p
zz
) и касательными (τ
xy
= τ
yx
; τ
yx
= τ
xy
; τ
zx
= τ
xz
), предE
ставив из (3)
p
xx
= –p + p′
xx
, (4)
где p′
xx
— добавочные нормальные напряжения, коE
торые и зависят от направления воздействия, по
аналогии с формулой (4) получим:
Сделав то же самое для компонентов p
yy
, p
zz
, полуE
чили систему.
'2 . (5)
y
xx
u
p
x
μ
∂
=
∂
.(3)
3
xx yy zz
ppp
p
++
=
ся достаточными всего шесть независимых комE
понентов:
p
xx
, p
yy
, p
zz
, τ
xy
(или τ
yx
), τ
xz
(τ
zx
), τ
yz
(τ
zy
).
Аналогичное уравнение легко можно получить для
осей O
Y
и O
Z
; объединив все три уравнения в систему,
получим (предварительно разделив на ρ):
Полученную систему называют уравнением дви&
жения вязкой жидкости в напряжениях.
1
1
.
1
yx
xx zx
yy xy zy
yz
zz xz
p
dUx
Fx
xyzdt
p
dUy
Fy
yxzdt
p
dUz
Fz
zxydt
τ
τ
ρ
ττ
ρ
τ
τ
ρ
⎧
∂
⎛⎞
∂∂
++ =
⎜⎟⎪
⎜⎟
∂∂∂
⎪
⎝⎠
⎪
∂∂∂
⎛⎞
⎪
++ =
⎜⎟
⎨
⎜⎟
∂∂∂
⎝⎠
⎪
⎪
∂
⎛⎞
∂∂
⎪
++ =
⎜⎟
⎜⎟
⎪
∂∂∂
⎝⎠
⎩
.
yx
xx zx
p
dUx
Fx
xyz dt
τ
τ
ρρ
∂
∂∂
+++=
∂∂∂
Полученное выражение есть не что иное, как
последнее, третье слагаемое в уравнении БерE
нулли. Следовательно, U
2
/ 2 — это удельная кинетичеE
ская энергия струйки. Таким образом, общий энергеE
тический смысл уравнения Бернулли таков: уравнение
Бернулли представляет собой сумму, содержащую в сеE
бе полную удельную энергию сечения жидкости в потоке:
1) если полная энергия соотнесена с единичной масE
сой, то она есть сумма gz + p/ρ + U
2
/ 2;
2) если полная энергия соотнесена с единичным объеE
мом, то ρgz + p + pU
2
/ 2;
3) если полная энергия соотнесена единичному весу, то
полная энергия есть сумма z + p/ρg + U
2
/ 2g. Не слеE
дует забывать, что удельная энергия определяется
относительно плоскости сравнения: эта плоскость
выбирается произвольно и горизонтально. Для люE
бой пары точек, произвольно выбранной из потока,
в котором установившееся движение и который двиE
жется потенциальноEвихрево, а жидкость невязкоE
несжимаемая, суммарная и удельная энергия одинаE
ковы, то есть распределены по потоку равномерно.
29б
30б
31б
32б
19
33. Уравнение Бернулли
для движения вязкой жидкости
Элементарная струйка при установившемся дви&
жении вязкой жидкости
Уравнение для этого случая имеет вид (приводим
его без вывода, поскольку его вывод сопряжен с приE
менением некоторых операций, приведение которых
усложнило бы текст):
Потеря напора (или удельной энергии) h
Пp
— реE
зультат того, что часть энергии превращается из меE
ханической в тепловую. Поскольку процесс необраE
тим, то имеет место потеря напора.
Этот процесс называется диссипацией энергии.
Другими словами, h
Пp
можно рассматривать как разE
ность между удельной энергией двух сечений, при
движении жидкости от одного к другому происходит
потеря напора. Удельная энергия — это энергия, коE
торую содержит единичная масса.
Поток с установившимся плавно изменяющем&
ся движением. Коэффициент удельной кинема&
тической энергии Х
Для того, чтобы получить уравнение Бернулли
в этом случае, приходится исходить из уравнения (1),
то есть из струйки надо переходить в поток. Но для
этого нужно определиться, что представляет собой
энергия потока (которая состоит из суммы потенE
циальной и кинематической энергий) при плавно изE
меняющемся потоке.
22
11 2 2
12
.(1)
22
Пp
pU pU
ZZh
gg gg
ρρ
++=+++
35. Уравнение Бернулли
для неустановившегося движения
вязкой жидкости
Для того, чтобы получить уравнение Бернулли, приE
дется определить его для элементарной струйки при
неустановившемся движении вязкой жидкости, а заE
тем распространять его на весь поток.
Прежде всего, вспомним основное отличие неустаноE
вившегося движения от установившегося. Если в перE
вом случае в любой точке потока местные скорости
изменяются по времени, то во втором случае таких изE
менений нет.
Приводим уравнение Бернулли для элементарной
струйки без вывода:
(КД)
υ
= ρυ
2
ω —
здесь учтено, что υω = Q; ρQ = m; mυ = (КД)
υ
.
Так же, как и в случае с удельной кинетической энерE
гией, считать (КД)
υ
не такEто просто. Чтобы считать,
нужно связать его с (КД)
υ
. Для этого служит коэффиE
циент количества движения
2
()
1
'.(3)
()
u
КД
u
ad
КД
ω
ω
υω υ
⎛⎞
==
⎜⎟
⎝⎠
∫
22
11 2 2
12прин
.(1)
22
pU pU
ZZhh
gg gg
ρρ
++=++++
36. Ламинарный и турбулентный ре&
жимы движения жидкости.
Число Рейнольдса
Как нетрудно было убедиться в вышеприведенном
опыте, если фиксировать две скорости в прямом и обE
ратном переходах движения в режимы ламинарное →
турбулентное, то
где υ
1
— скорость, при которой начинается переход
из ламинарного в турбулентный режим;
υ
2
— то же самое при обратном переходе.
Как правило, υ
2
< υ
1
. Это можно понять из определеE
ния основных видов движения.
Ламинарным (от лат. lamina — слой) считается таE
кое движение, когда в жидкости нет перемешивания
частиц жидкости; такие изменения в дальнейшем буE
дем называть пульсациями.
Движение жидкости турбулентное (от лат. turbulen3
tus — беспорядочный), если пульсация местных скоE
ростей приводит к перемешиванию жидкости.
Скорости перехода υ
1
, υ
2
называют:
υ
1
— верхней критической скоростью и обознаE
чают как υ
в.кр
, это скорость, при которой ламинарное
движение переходит в турбулентное;
υ
2
— нижней критической скоростью и обознаE
чают как υ
н.кр
, при этой скорости происходит обратный
переход от турбулентного к ламинарному.
Значение υ
в.кр
зависит от внешних условий (термодиE
намические параметры, механические условия), а знаE
чения υ
н.кр
не зависят от внешних условий и постоянны.
12
,
υυ
≠
34. Гидродинамический удар. Гидро&
и пьезо& уклоны
В силу плавности движения жидкости для любой
точки живого сечения потенциальная энергия Еп = Z +
+ p/ρg. Удельная кинетическая Е
k
= Xυ
2
/2g. Поэтому
для сечения 1—1 полная удельная энергия
Сумму правой части (1) также называют гидроди&
намическим напором Н. В случае невязкой жидкоE
сти U
2
= xυ
2
. Теперь остается учесть потери напора h
пр
жидкости при ее движении к сечению 2—2 (или 3—3).
Например, для сечения 2—2:
Следует отметить, что условие плавной изменяемоE
сти должно быть выполнено только в сечениях 1—1
и 2—2 (только в рассматриваемых): между этими сеE
чениями условие плавной изменяемости необязаE
тельно.
В формуле (2) физический смысл всех величин приE
веден ранее.
В основном все так же, как и в случае с невязкой
жидкостью, основная разница в том, что теперь напорE
ная линия Е = Н = Z + p/ρg + Xυ
2
/2g не параллельна к гоE
ризонтальной плоскости сравнения, поскольку имеет
места потери напора.
2
222
22 пр
.(2)
2
px
EE h
gg
υ
ρ
=++ + +
2
111
111
Z.(1)
2
k
px
EEnE
gg
υ
ρ
=+ =+ +
33а
34а
35а
36а
33а
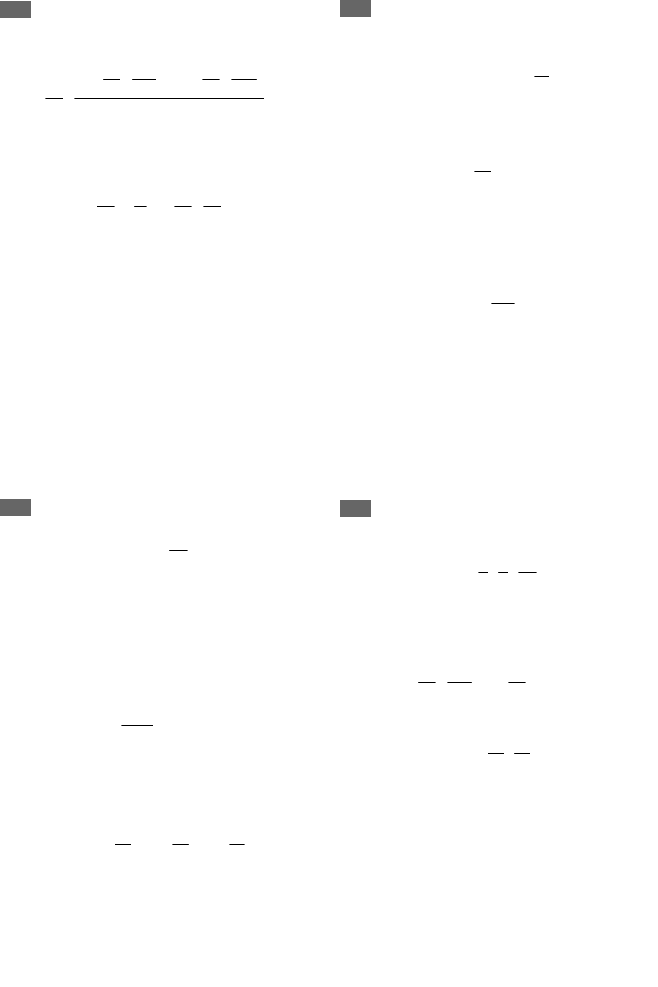
20
Степень потери напора h
пр
по длине называют
гидравлическим уклоном J. Если потеря напоE
ра h
пр
происходит равномерно, то
Числитель в формуле (3) можно рассматривать как
приращение напора dH на длине dl.
Поэтому в общем случае
Знак минус перед dH/dl — потому, что изменение наE
пора по его течению отрицательно.
Если рассмотреть изменение пьезометрического
напора Z + p/ρg, то величину (4) называют пьезомет&
рическим уклоном.
Напорная линия, она же линия удельной энергии,
находится выше пьезометрической линии на высоту
u
2
/2g: здесь то же самое, но только разница между этиE
ми линиями теперь равна xυ
2
/2g. Эта разница сохраE
няется также при безнапорном движении. Только
в этом случае пьезометрическая линия совпадает со
свободной поверхностью потока.
.(4)
2
dH d p X
JZ
dl dl g g
υ
ρ
⎛⎞
==− ++
⎜⎟
⎝⎠
22
111 222
12
пр
2g 2g
.(3)
px px
z+ + + +
hg g
J
ll
υυ
υ
ρρ
⎛⎞⎛ ⎞
−
⎜⎟⎜ ⎟
⎜⎟⎜ ⎟
⎝⎠⎝ ⎠
==
Эмпирическим путем установлено, что:
где V — кинематическая вязкость жидкости;
d — диаметр трубы;
R — коэффициент пропорциональности.
В честь исследователя вопросов гидродинамики воE
обще и данного вопроса в частности, коэффициент, соE
ответствующий uн.кр, называется критическим чи&
слом Рейнольдса Re
кр
.
Если изменить V и d, то Re
кр
не изменяется и остаетE
ся постоянным.
Если Re < Re
кр
, то режим движения жидкости лами&
нарный, поскольку υ < υ
кр
; если Re > Re
кр
, то режим
движения турбулентный изEза того, что υ > υ
кр
.
;;.
dR h
dRh
Re Re = Re =
VVV
υυυ
=
н.кр
кр
2320 .
Л
KRe
V
υ
===
н.кр
,
RV
d
υ
=
Коэффициент a′ принято называть еще и коэф&
фициентом Бусинеска. С учетом a′, средний
инерционный напор по живому сечению
Окончательно уравнение Бернулли для потока, поE
лучение которого и являлось задачей рассматриваеE
мого вопроса имеет следующий вид:
где
Что касается (5), то оно получено из (4) с учетом тоE
го, что dQ = wdu; подставив dQ в (4) и сократив ω, приE
ходим к (6).
Отличие h
ин
от h
пр
прежде всего в том, что оно не явE
ляется необратимым. Если движение жидкости с ускоE
рением, что значит dυ/t > 0, то h
ин
> 0. Если движение
замедленное, то есть du/t < 0, то h
ин
< 0.
Уравнение (5) связывает параметры потока только
в данный момент времени. Для другого момента оно
может уже оказаться не достоверным.
1
ин
.(6)
xl
d
h
gdt
υ
=×
2
111 2
12прин
,(5)
2
px p
ZZhh
gg g
υ
ρρ
++ =+++
ин
1
.(4)
adQ
h
gdt
ω
=××
Разберемся с потенциальной энергией: при
плавном изменении движения, если поток устаE
новившийся,
Окончательно при рассматриваемом движении давE
ление по живому сечению распределено согласно гидроE
статическому закону, т. е.
Е
ku
= ХЕ
k
υ, (4)
где величину Х называют коэффициентом кинети&
ческой энергии, или коэффициентом Кориолиса.
Коэффициент Х всегда больше 1. Из (4) следует:
2
.(5)
2
ku
X
E
g
υ
=
const. (3)
p
Z
pg
+=
;0;0;0. (2)
u
Ux U Uy Uz
t
∂
≈≈≈=
∂
33б
34б
35б
36б
