Шпоры - Ответы на билеты к кандидатскому экзамену

Подождите немного. Документ загружается.

Билет 3

1. Принципы и структура системного анализа

Методология системного анализа представляет собой довольно сложную и пеструю совокупность

принципов, подходов, концепций и конкретных методов.

Под принципами понимаются основные, исходные положения, некоторые общие правила познавательной

деятельности, которые указывают направление научного познания, но не дают указания на конкретную

истину. Это выработанные и исторически обобщенные требования к познавательному процессу,

выполняющие важнейшие регулятивные роли в познании. Обоснование принципов – первоначальный этап

построения методологической концепции.

К важнейшим принципам системного анализа следует отнести принципы элементаризма, всеобщей связи,

развития, целостности, системности, оптимальности, иерархии, формализации, нормативности и

целеполагания. Системный анализ представляется интегралом данных принципов.

Табл. 1 Принципы системного анализа и их характеристика

Принципы системного

анализа

,Характеристика

Элементаризма Система представляет собой совокупность взаимосвязанных элементарных

составляющих

Всеобщей связи Система выступает как проявление универсального взаимодействия предметов и

явлений

Развития Системы находятся в развитии, проходят этапы возникновения, становления,

зрелости и нисходящего развития

Целостности Рассмотрение любого объекта, системы с точки зрения внутреннего единства,

отделенности от окружающей среды

Системности Рассмотрение объекта как системы, т.е. как целостности, которая не сводится к

совокупности элементов и связей

Оптимальности Любая система может быть приведена в состояние наилучшего ее

функционирования с точки зрения некоторого критерия

Иерархии Система представляет собой соподчиненное образование

Формализации Любая система с большей или меньшей корректностью может быть

представлена формальными моделями, в т.ч. формально-логическими,

математическими, кибернетическими и др.

Нормативности Любая система может быть понята только в том случае, если она будет

сравниваться с некоторой нормативной системой

Целеполагания Любая система стремится к определенному предпочтительному для него

состоянию, выступающему в качестве цели систем

Методологические подходы в системном анализе объединяют совокупность сложившихся в практике

аналитической деятельности приемов и способов реализации системной деятельности. Наиболее важными

среди них выступают системный, структурно-функциональный, конструктивный, комплексный,

ситуационный, инновационный, целевой, деятельностный, морфологический и программно-целевой

подходы.

Методологический комплекс системного анализа был бы неполным, если в нем не выделить его

теоретический ансамбль. Теория является не только отражением действительности, но и методом ее

отражения, т.е. она выполняет методологическую функцию. На этом основании системные теории

включаются в системный методологический комплекс.

Системная теория развивается по нескольким направлениям. Практически исчерпывает себя такое

направление, как общая теория систем, сформировался структурализм, функционализм и структурный

функционализм в обществознании, биологии, получили развитие системно-кибернетические и

математические теории. Наиболее перспективным направлением ныне является синергетика, которая дает

объяснение нестандартным системам, с которыми человек сталкивается все чаще в условиях перехода к

постиндустриальной динамике жизни.

Многообразие методологии системного анализа выступает питательной почвой для развития

разновидностей системного анализа, под которым понимаются некоторые сложившиеся методологические

комплексы. Вопрос о классификации разновидностей системного анализа еще не разработан в науке.

Имеются отдельные подходы к этой проблеме, которые встречаются в некоторых работах. Довольно часто

виды системного анализа сводят к методам системного анализа или к специфике системного подхода в

системах различной природы. На самом деле бурное развитие системного анализа приводит к

дифференциации его разновидностей по многим основаниям, в качестве которых выступают: назначение

системного анализа; направленность вектора анализа; способ его осуществления; время и аспект системы;

отрасль знания и характер отражения жизни системы.

структуре общего системного анализа выделяются несколько составляющих. Наиболее важные – это

структурный, функциональный, факторный, генетический и временной анализы. Конкретные разновидности

главенствующий элемент

1-й иерархический уровень

2-й иерархический уровень

аналитической деятельности могут ограничиваться отдельными их разновидностями.

Табл. 6. Структура системного анализа

Составляющие

системного анализа

Вид Характеристика

Структурный Макроструктурный Выделение системы из среды, определение

факторов, которые на нее воздействуют, и того,

частью какой системы является данная система

Микроструктурный Изучение строения системы вплоть до

элементарности

Функциональный Внешний Выяснение воздействий внешних функций

системы

Внутренний Выделение внутренних функций системы

Факторный Макрофакторный Выделение факторов макросреды, которые

воздействуют на систему

Микрофакторный Выделение факторов микросреды, которые

воздействуют на систему

Генетический Макроанализ Исследование происхождения системы с точки

зрения макрохарактеристик

Микроанализ Исследование происхождения системы с точки

зрения микрохарактеристик

Временной Прогностический Выяснение будущего системы и ее составляющих

Исторический Предполагающий исследование прошлых

состояний системы

Выводы

Системный анализ представляется в виде некоторого множества более конкретных его разновидностей. Это

множество «простых» системных подходов можно представить в виде матрицы, в каждой ячейке которой

находится один из частных методов.

Матрица системного анализа дает представление обо всех возможных разновидностях системного анализа.

Она выступает классификатором, своеобразным путеводителем по системному анализу. Одновременно она

служит в качестве методологического прогноза относительно перспектив развития системного анализа.

Реальное состояние системной аналитики ныне таково, что развито небольшое число конкретных методов

системного анализа. Матрица практически пустая. Ее заполнение – очень важная и одновременно сложная

задача науки, которая должна не только отработать технологии методов, но и применять их к решению

задач системного анализа.

Системный анализ – это сложная наука, которая находится в процессе становления, обретения своей

системы, представленной матрицей системного анализа.

2. Методы экспертных оценок

Изучению возможностей и особенностей применения экспертных оценок посвящено много работ. В них

рассматриваются формы экспертного опроса (разные виды анкетирования, интервью), подходы к

оцениванию (ранжирование, нормирование, различные виды упорядочения и т. д.), методы обработки

результатов опроса, требования к экспертам и формированию экспертных групп, вопросы тренировки

экспертов, оценки их компетентности (при обработке оценок вводятся и учитываются коэффициенты

компетентности экспертов, достоверности их мнений), методики организации экспертных опросов.

Выбор форм и методов проведения экспертных опросов, подходов к обработке результатов опроса и т. д.

зависит от конкретной задачи и условий проведения экспертизы. Однако существуют некоторые общие

проблемы, которые нужно помнить специалисту по системному анализу. Остановимся на них подробнее.

Возможность использования экспертных оценок, обоснование их объективности обычно базируется на том,

что неизвестная характеристика исследуемого явления трактуется как случайная величина, отражением

закона распределения которой является индивидуальная оценка специалиста-эксперта о достоверности и

значимости того или иного события. При этом предполагается, что истинное значение исследуемой

характеристики находится внутри диапазона оценок, получаемых от группы экспертов, и что обобщенное

коллективное мнение является достоверным.

Однако в некоторых теоретических исследованиях это предположение подвергается сомнению. Например,

некоторыми специалистами предлагается разделить проблемы, для решения которых применяются

экспертные оценки, на два класса. К первому классу относятся проблемы, которые достаточно хорошо

обеспечены информацией и для которых можно использовать принцип «хорошего измерителя», считая

эксперта хранителем большого объема информации, а групповое мнение экспертов — близким к истинному.

Ко второму классу относятся проблемы, в отношении которых знаний для уверенности в справедливости

названных предположений недостаточно; экспертов нельзя рассматривать как «хороших измерителей», и

главенствующий элемент

1-й иерархический уровень

2-й иерархический уровень

необходимо осторожно подходить к обработке результатов экспертизы, поскольку в этом случае мнение

одного (единичного) эксперта, больше внимания, чем другие, уделяющего исследованию малоизученной

проблемы, может оказаться наиболее значимым, а при формальной обработке оно будет утрачено. В связи с

этим к задачам второго класса в основном должна применяться качественная обработка результатов.

Использование методов осреднения (справедливых для «хороших измерителей») в данном случае может

привести к существенным ошибкам.

Задачи коллективного принятия решений по формированию целей, совершенствованию методов и форм

управления обычно можно отнести к первому классу. Однако при разработке прогнозов и перспективных

планов целесообразно выявлять «редкие» мнения и подвергать их более тщательному анализу.

Другая проблема, которую нужно иметь в виду при проведении системного анализа, заключается в

следующем: даже в случае решения проблем, относящихся к первому классу, нельзя забывать о том, что

экспертные оценки несут в себе не только субъективные черты, присущие отдельным экспертам, но и

коллективно-субъективные черты, которые не исчезают при обработке результатов опроса (а при

применении Дельфи-процедуры даже могут усиливаться). Иными словами, на экспертные оценки нужно

смотреть как на некоторую «общественную точку зрения», зависящую от уровня научно-технических

знаний общества относительно предмета исследования, которая может меняться по мере развития системы и

наших представлений о ней. Следовательно, экспертный опрос — это не одноразовая процедура. Такой

способ получения информации о сложной проблеме, характеризующейся большой степенью

неопределенности, должен стать своего рода «механизмом» в сложной системе, т. е. необходимо создать

регулярную систему работы с экспертами.

Следует обратить также внимание на то, что использование классического частотного подхода к оценке

вероятности при организации проведения экспертных опросов бывает затруднительным, а иногда и

невозможным (из-за невозможности доказать правомерность использования представительности выборки).

Поэтому в настоящее время ведутся исследования характера вероятности экспертной оценки, базирующиеся

на теории размытых множеств Заде, на представлении об экспертной оценке как степени подтверждения

гипотезы или как вероятности достижения цели (последнее направление развивается на основе

информационного подхода).

Метод «Дельфи» или метод «дельфийского оракула» первоначально был предложен О. Хелмером и его

коллегами как итеративная процедура при проведении мозговой атаки, которая способствовала бы

снижению влияния психологических факторов при повторении заседаний и повышении объективности

результатов. Однако почти одновременно «Дельфи»-процедуры стали средством повышения объективности

экспертных опросов с использованием количественных оценок при оценке «деревьев цели» и при

разработке «сценариев».

В отличие от традиционных методов экспертной оценки метод Дельфи предполагает полный отказ от

коллективных обсуждений. Это делается для того, чтобы уменьшить влияние таких психологических

факторов, как присоединение к мнению наиболее авторитетного специалиста, нежелание отказаться от

публично выраженного мнения, следование за мнением большинства. В методе Дельфи прямые дебаты

заменены программой последовательных индивидуальных опросов, проводимых в форме анкетирования.

Ответы обобщаются и вместе с новой дополнительной информацией поступают в распоряжение экспертов,

после чего они уточняют свои первоначальные ответы. Такая процедура повторяется несколько раз до

достижения приемлемой сходимости совокупности высказанных мнений. Результаты эксперимента

показали приемлемую сходимость оценок экспертов после пяти туров опроса. Метод Дельфи первоначально

был предложен О. Хелмером как итеративная процедура «мозговой атаки», которая должна помочь снизить

влияние психологических факторов и повысить объективность результатов. Однако почти одновременно

Дельфи-процедуры стали основным средством повышения объективности экспертных опросов с

использованием количественных оценок при оценке деревьев цели и при разработке сценариев за счет

использования обратной связи, ознакомления экспертов с результатами предшествующего тура опроса и

учета этих результатов при оценке значимости мнений экспертов.

Процедура Дельфи-метода заключается в следующем:

1) организуется последовательность циклов «мозговой атаки»;

2) разрабатывается программа последовательных индивидуальных опросов с помощью вопросников,

исключающая контакты между экспертами, но предусматривающая ознакомление их с мнениями друг друга

между турами; вопросники от тура к туру могут уточняться;

3) в наиболее развитых методиках экспертам присваиваются весовые коэффициенты значимости их мнений,

вычисляемые на основе предшествующих опросов, уточняемые от тура к туру и учитываемые при

получении обобщенных результатов оценок.

Первое практическое применение метода Дельфи к решению некоторых задач министерства обороны США,

осуществленное RAND Corporation во второй половине 40-х гг., показало его эффективность и

целесообразность распространения на широкий класс задач, связанный с оценкой будущих событий.

Недостатки метода Дельфи:

• значительный расход времени на проведение экспертизы, связанный с большим количеством

последовательных повторений оценок;

главенствующий элемент

1-й иерархический уровень

2-й иерархический уровень

• необходимость неоднократного пересмотра экспертом своих ответов, вызывающая у него отрицательную

реакцию, что сказывается на результатах экспертизы.

В 60-е гг. область практического применения метода Дельфи значительно расширилась, однако присущие

ему ограничения привели к возникновению других методов, использующих экспертные оценки. Среди них

особого внимания заслуживают методы

QUEST, SEER, PATTERN.

Метод QUEST (Qualitative Utility Estimates for Science and Technology - количественные оценки полезности

науки и техники) был разработан для целей повышения эффективности решений по распределению

ресурсов, выделяемых на исследования и разработки. В основу метода положена идея распределения

ресурсов на основе учета возможного вклада (определяемого метода экспертной оценки) различных

отраслей и научных направлений в решение какого-либо круга задач. Метод SEER (System for Event

Evaluation and Review система оценок и обзора событий) предусматривает всего два тура оценки. В каждом

туре привлекается различный состав экспертов. Эксперты первого тура - специалисты промышленности,

эксперты второго тура - наиболее квалифицированные специалисты из органов, принимающих решения, и

специалисты в области естественных и технических наук. Эксперт каждого тура не возвращается к

рассмотрению своих ответов за исключением тех случаев, когда его ответ выпадает из некоторого

интервала, в котором находится большинство оценок (например, интервала, в котором находится 90 % всех

оценок).

главенствующий элемент

1-й иерархический уровень

2-й иерархический уровень

Билет 1

1.Энтропия системы и дискретных источников сообщений

До сих пор определялось количество информации, содержащееся в отдельных сообщениях. Вместе с тем во

многих случаях, когда требуется согласовать канал с источником сообщений , таких сведений оказывается

недостаточно. Возникает потребность в характеристиках, которые позволяли бы оценивать

информационные свойства источника сообщений в целом. Одной из важных характеристик такого рода

является среднее количество информации, приходящееся на одно сообщение. В простейшем случае, когда

все сообщения равновероятны, количество информации в каждом из них одинаково и определяется

выражением: J(a)= - logP(a)= log m. При этом среднее количество информации равно logm . Следовательно,

при равновероятных независимых сообщениях информационные свойства источника зависят только от

числа сообщений в ансамбле m. Однако в реальных условиях сообщения, как правило, имеют разную

вероятность. Так, буквы алфавита О, Е, А встречаются в тексте сравнительно часто, а буквы Щ, Ы, Ъ —

редко. Поэтому знание числа сообщений m в ансамбле является недостаточным, необходимо иметь сведения

о вероятности каждого сообщения: P(a

), P(a

),…, P(a

). Так как вероятности сообщений неодинаковы, то

они несут различное количество информации: J(a

) = - logP(a

) Менее вероятные сообщения несут большее

количество информации и наоборот. Среднее количество информации, приходящееся на одно сообщение

источника, определяется как математическое ожидание J(a

Величина Н(а) называется энтропией. Этот термин

заимствован из термодинамики, где имеется аналогичное по

своей форме выражение, характеризующее неопределенность

состояния физической системы. В теории информации

энтропия Н(а) также характеризует неопределенность

ситуации до передачи сообщения, поскольку заранее неизвестно, какое из сообщений ансамбля источника

будет передано. Для нас самым существенным является то, что чем больше энтропия, тем сильнее

неопределенность и тем большую информацию в среднем несет одно сообщение источника.

В качестве примера вычислим энтропию источника сообщений, который характеризуется ансамблем,

состоящим из двух сообщений a

и а

с вероятностями P(a

)=p и P(a

)=1-p. На основании (6.10) энтропия

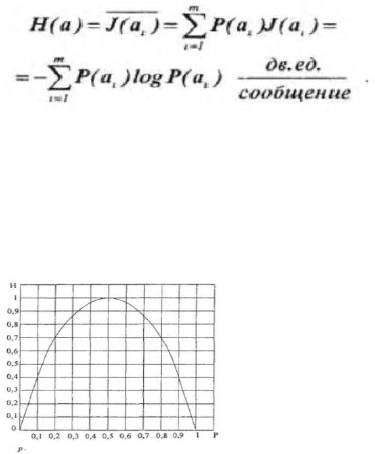
такого источника будет равна: H(a)= -P(a1) log P(a1) –P(a2) log P(a2) = --p log p- (1-p)lop(1-p) Зависимость

Н(а) от р показана на рис

Максимум энтропии имеет место при p=1/2, т. е. когда ситуация является

наиболее неопределенной. При р = 1 или р = 0, что соответствует передаче

одного из сообщений а

, или а

, неопределенности отсутствуют. В этих случаях

энтропия Н(а) равна нулю.

Среднее количество информации, содержащееся в последовательности из n-

сообщений, равно Jn = n*H(a). Отсюда следует, что количество передаваемой

информации можно увеличить не только за счет числа сообщений, но и путем

повышения энтропии источника, т. е. информационной емкости его сообщений.

Обобщая эти результаты, можно сформулировать основные свойства энтропии источника независимых

сообщений (6.10):

• энтропия — величина всегда положительная, так как 0<P(ai)<=1 • при равновероятных сообщениях,

когда: P(a1)= P(a2)=…= P(am)= P(a)=1/m энтропия максимальна и равна:Hmax(a)=H0(a)= SUM((i=1..m)1/

m log m)= log m • энтропия равняется нулю лишь в том случае, когда все вероятности P(a

) равны нулю, за

исключением одной, величина которой равна единице; • энтропия нескольких независимых источников

равна сумме энтропии этих источников: H(a,b,...,r)=H(a)+ (b) + + ... + Н(r).

Энтропия источника зависимых сообщений

Рассмотренные выше источники независимых сообщений являются простейшим типом источников. В

реальных условиях картина значительно усложняется из-за наличия статистических связей между

сообщениями. Примером может быть обычный текст, где появление той или иной буквы зависит от

предыдущих буквенных сочетаний. Так, например, после сочетания ЧТ вероятность следования гласных

букв О, Е, И больше, чем согласных.

Статистическая связь ожидаемого сообщения с предыдущим сообщением количественно оценивается

совместной вероятностью P(a

) или условной вероятностью P(a

), которая выражает вероятность

появления сообщения a

при условии, что известно предыдущее сообщение а

. Количество информации,

содержащейся в сообщении при условии, что известно предыдущее сообщение а

согласно (6.1), будет

равно: J(a l/a k)= - log P (a l/a k)

Среднее количество информации при этом определяется условной энтропией H(a

), которая вычисляется

как математическое ожидание информации J(a

), по всем возможным сообщениям a

и a

Важным свойством условной энтропии источника зависимых сообщений является то, что при неизменном

количестве сообщений в ансамбле источника его энтропия уменьшается с увеличением числа сообщений,

между которыми существует статистическая взаимосвязь. В соответствии с этим свойством, а также

главенствующий элемент

1-й иерархический уровень

2-й иерархический уровень

свойством энтропии источника независимых сообщений можно записать неравенства: H0(a)>= H1(a)>=…

>=Hn(a)

Таким образом, наличие статистических связей между сообщениями всегда приводит к уменьшению

количества информации, приходящейся в среднем на одно сообщение.

2. Основные определения и теоремы теории игр

Конфликт - это противоречие, вызванное противоположными интересами сторон.

Конфликтная ситуация - ситуация в которой участвуют стороны интересы которых полностью

или частично противоположны.

Игра - это действительный или формальный конфликт, в котором имеется по крайней мере два

участника, каждый из которых стремится к достижению собственных целей

Правилами игры называют допустимые действия каждого из игроков, направленные на

достижение некоторой цели.

Платежом называется количественная оценка результатов игры.

Парная игра - игра в которой участвуют только две стороны (два игрока).

Игра с нулевой суммой - парная игра при которой сумма платежа равна нулю, т. е. если проигрыш

одного игрока, равен выигрышу другого.

Стратегия игрока - это однозначный выбор игрока в каждой из возможных ситуаций, когда этот

игрок должен сделать личный ход.

Оптимальная стратегия - это такая стратегия игрока, которая при многократном повторении игры

обеспечивает ему максимально возможный средний выигрыш или минимально возможный средний

проигрыш.

Пусть мы имеем парную игру с нулевой суммой, один игрок может выбрать при данном ходе i -ю

стратегию из m своих возможных (i=1..m), а второй, не зная выбора первого j -ю стратегию из n своих

возможных стратегий (j=1..n). В результате первый игрок выигрывает величину

, а второй проигрывает

эту величину. Из этих величин составим матрицу A.

( )a

Платежная матрица - так назовем матрицу A или еще по другому

матрицей игры.

Конечной игрой размерности (m  n) называется игра определенная матрицей А имеющей m

строк и n столбцов.

Максимином или нижней ценой игры назавем число

 max( min )

i j

, а соответствующая

ему стратегия (строка) максиминной.

Минимаксом или верхней ценой игры назавем число ,

)max(min

a



а соответствующая

ему стратегия (столбец) минимаксной.

Теорема 1.1. Нижняя цена игры всегда не превосходит верхнюю цену игры.

Игрой с седловой точкой называется игра для которой

 

Ценой игры называется величина



, если

   

В случае игры с седловой точкой , игрокам выгодно придерживатся максиминной и минимаксной

стратегий и не выгодно отклонятся от них . В таких случаях про игру говорят, что в ней имеет место

равновесие в чистых стратегиях. Возможна игра и с несколькими седловыми точками. Тогда игра имеет

несколько оптимальных решений, но с одинаковой ценой игры. Чаще встречаются матричные игры без

седловой точки, когда    и тогда для нахождения её решения используются смешанные стратегии.

Смешанной стратегией игрока называется вектор, каждая из компонент которого показывает

относительную частоту использования игроком соответствующей чистой стратегии.

Теорема 1.2. Основная теорема теории матричных игр. Всякая матричная игра с нулевой суммой

имеет решение в смешанных стратегиях.

главенствующий элемент

1-й иерархический уровень

2-й иерархический уровень

















mnmm

aaa



22221

11211

Теорема 1.3. Если один из игроков применяет оптимальную смешанную стратегию, то его

выигрыш равен цене игры  в не зависимости от того, с какими частотами будет применять второй игрок

свои стратегии (в том числе и чистые стратегии).

главенствующий элемент

1-й иерархический уровень

2-й иерархический уровень

Билет 2

1. Принцип необходимого разнообразия

BЗакон необходимого разнообразия. По определению У. Р. Эшби, первый

фундаментальный закон кибернетики заключается в том, что разнообразие сложной

системы требует управления, которое само обладает некоторым разнообразием. Иначе

говоря, значительное разнообразие воздействующих на большую и сложную систему

возмущений требует адекватного им разнообразия её возможных состояний. Если же

такая адекватность в системе отсутствует, то это является следствием нарушения

принципа целостности составляющих её частей (подсистем), а именно - недостаточного

разнообразия элементов в организационном построении (структуре) частей.

,,,,,,,Ограничение разнообразия в поведении управляемого объекта достигается только за

счет увеличения разнообразия органа управления (управленческих команд). Чтобы

достигнуть минимума разнообразия выходных реакций (результатов деятельности)

системы, управляющий орган должен быть способен к выработке определенного

минимума команд и сигналов. Если его мощность ниже минимума, он не способен

обеспечить полное управление.

,,,,,,,Процесс управления в конечном счете сводится к уменьшению разнообразия

состояний управляемой системы, к уменьшению её неопределенности. В соответствии с

этим законом, с увеличением сложности управляемой системы сложность управляемого

блока также должна повышаться. Поэтому все большее усложнение аппарата управления

корпорациями, холдингами, финансово-промышленными группами, и т. п. организациями

и их частями в современных условиях - это закономерный процесс. Другое дело, что

восполнять разнообразие управляющей системы нужно за счет внедрения компьютерных

и других прогрессивных технологий управления и математических методов, а не за счет

привлечения дополнительных людских ресурсов.

,,,,,,,Закон необходимого разнообразия

имеет принципиальное значение для разработки

оптимальной структуры системы управления. Если центральный орган управления при

сохранении разумных размеров не обладает необходимым разнообразием, то следует

развивать иерархическую структуру, передавая принятие определенных решений на

нижние уровни и не допуская, чтобы они превращались в передаточные инстанции.

Неудовлетворительные результаты проводимой в стране экономической реформы

объясняются неадекватной реакцией органов управления. В стране увеличивается

разнообразие форм собственности, разновидностей структурных формирований объектов

управления, моделей хозяйствования и т. п. В соответствии с этими изменениями

необходимо систему управления таким развитием привести в соответствие с законом

необходимого разнообразия (обеспечить льготное кредитование структурных

преобразований, разумное налогообложение развивающихся предприятий,

государственную политику подготовки и переподготовки кадров и т. п. ).

,,,,,,,С позиции теории управления главнейшим моментом, характеризующим сложность

системы, является её разнообразие. Поэтому определение степени оптимального

разнообразия при разработке любых систем - организации производства, планирования,

обслуживания, оперативного управления, систем оплаты труда и т. д. - является одним

из наиболее важных и первоочередных этапов использования кибернетики при

проектировании и функционировании организации.

2. Аксиомы теории управления

Аксиома 1. Наличие наблюдаемости объекта управления. В теории управления ОУ

считается наблюдаемым в состоянии z(t) на множестве моментов времени Т при входном

воздействии ХО) и отсутствии возмущений, если уравнение наблюдения динами ческой

системы, представленное в виде y*(t) = g[t,x(t),z*(t)], где у *(t) — некоторая реализация

главенствующий элемент

1-й иерархический уровень

2-й иерархический уровень

выходного процесса, доступная для регистрации, имеет единственное решение z*(t) =

z(t)О Х Если это утверждение справедливо для любого z(t)О Х, то объект считается

полностью наблюдаемым. Это выражение означает, что определение любого из состояний

ОУ (т.е. его наблюдаемость) реализуется только в том слу чае, если по результатам

измерения выходных переменных у*(t) при известных значениях входных переменных

x(t) может быть получена оценка z*(t) любой из переменных состояния z(t). Такая задача в

теории систем известна как задача наблюдения. В организационно-технических системах

управления эта задача реализуется функцией контроля текущего состояния ОУ и воз

действий внешней среды. Без этой информации управление или невозможно, или

неэффективно.

Аксиома 2. Наличие управляемости — способности ОУ переходить в пространстве

состояний Z из текущего состояния в требуемое под воздействиями управляющей

системы. Под этим можно понимать перемещение в физическом пространстве, изменение

скорости и направления движения в пространстве состояний, изменение структуры или

свойств ОУ. Если состояние ОУ не меняется, то понятие управления теряет смысл.

Аксиома З. Наличие цели управления. Под целью управления понимают набор значений

количественных или качественных характеристик, определяющих требуемое состояние

ОУ. Если цель неизвестна, управление не имеет смысла, а изменение состояний

превращается в бесцельное блуждание. Цель отображается точкой, в которую надо

перевести систему из существующего состояния, или траекторией перевода ОУ в

требуемое состояние в виде, например, аддитивной свертки ,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,

с ограничениями типа ,, ,, где yi – i-я характеристика,

ai – важность (вес) i-й характеристики, bi – расход ресурсов на поддержании i-й

характеристики в требуемом состоянии, c – ,общее количество ресурсов.

Аксиома 4. Свобода выбора — возможность выбора управляющих воздействий

(решений) из некоторого множества допустимых альтернатив. Чем меньше это

множество, тем менее эффективно управление, так как в условиях ограничений

оптимальные решения часто остаются за пределами области адекватности. Если имеется

единственная альтернатива, то управление не требуется. Если решения не влияют на

изменение состояния СУ, то управления не существует.

Аксиома 5. Наличие критерия эффективности управления. Обобщенным критерием

эффективности управления считается степень достижения цели функционирования

системы.

Кроме степени достижения цели качество управления можно оценивать по частным

критериям: степени соответствия управляющих воздействий требуемым состояниям ОУ,

качеству принимаемых решений, точности управления. Для оценки систем управления

военного назначения вводятся требования к управлению по показателям устойчивости,

непрерывности (длительности цикла управления), оперативности и скрытности.

Аксиома 6. Наличие ресурсов (материальных, финансовых, трудовых и т.д.),

обеспечивающих реализацию принятых решений. Отсутствие ресурсов равносильно

отсутствию свободы выбора. Управление без ресурсов невозможно.

главенствующий элемент

1-й иерархический уровень

2-й иерархический уровень

Билет 4

1. Структура системы с управлением

Структура системы – расчленение ее на группы элементов с указанием связей

между ними, неизменное на все время рассмотрения и дающее представление о

системе в целом.

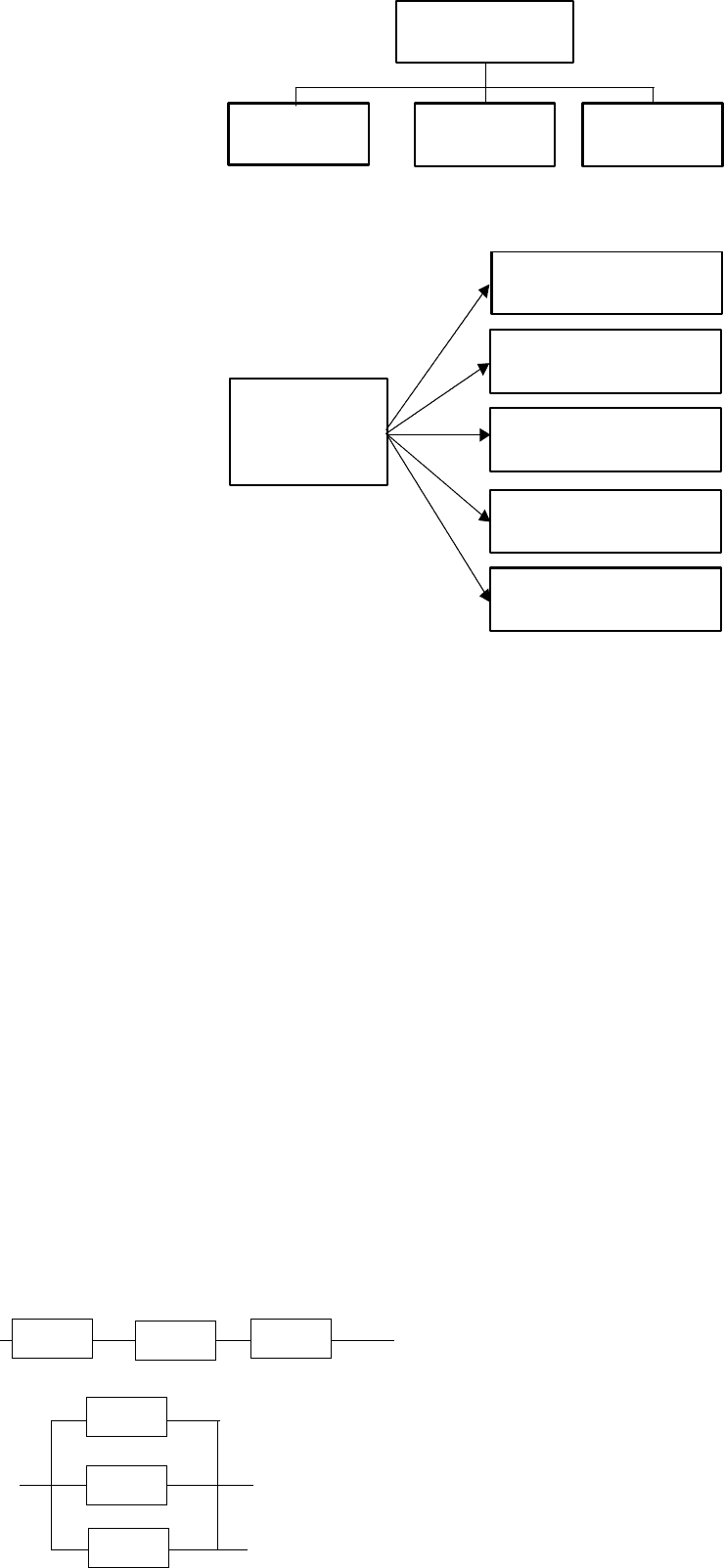
Расчленение системы может иметь различную основу:

 материальную (вещественную) (рис. 3а);

 функциональную (рис. 3б);

 алгоритмическую (алгоритм программы, инструкция).

Группы элементов в структуре обычно выделяются по принципу простых или

относительно более слабых связей между элементами разных групп. Структура

системы обычно изображается в виде графической схемы (структурной схемы).

Структуры других типов;

 календарь (временная структура);

 деление книги на главы (информационная структура).

Структура системы может быть охарактеризована по имеющимся в ней (или

преобладающим) типам связей:

а) последовательное соединение элементов;

Человек

Машины,

механизмы

Предмет

труда

Машинное

производство

Управление

безопасностью

труда

Планирование мероприятий

по охране труда

Организация работ по

охране труда

Анализ и оценка условий

труда

Контроль условий и

состояния охраны труда

Мотивация работ по охране

труда

Рис.3

главенствующий элемент

1-й иерархический уровень

2-й иерархический уровень