Shen S., Tuszynski J.A. Theory and Mathematical Methods for Bioformatics

Подождите немного. Документ загружается.

284 10 3D Structure of the Protein Backbone and Side Chains

Fig. 10.2a,b. Types E and Z for four-atom point conﬁgurations

Determination of Type E and Type Z

We use geometry to determine the type E and type Z conﬁguration of four-

atom points. Let π

and π

represent planes determined by the three points

a, b, c and b, c, d, respectively. Their normal vectors are b

and b

, where the

direction of the vectors is determined by the right-handed coordinate system,

that is, their mixed product

, r

, b

] , [r

, r

, b

] > 0 .

Using the correlation of the normal vectors b

and b

, we obtain the determin-

ing relationship for the structure type of the four-atom points conformation:

Theorem 38. The determining relationship of the type E and Z structures

of the four-atom points conﬁguration is as follows: If b

, b

 < 0, then the

conformation of the four-atom points a, b, c, d is of type E, if b

, b

 > 0, then

the conformation of the four-atom points a, b, c, d is of type Z.

Proof. We take the following steps to prove this proposition:

1. Because point d



is the projection of point d in plane Π

, we set vector



−→



to be the projection of r

−→

cd in plane Π

.Ifwedenotethe

normal vector of plane c, d



d by n = b

× r

,thenn is in plane Π

and

upright to r

, b

.Atthistime,r

, r



,andn are all in plane Π



Iﬀ (r

· n)(r



·n) > 0 , then d, d



are on the same side of r

Iﬀ (r

· n)(r



·n) < 0 , then d, d



are on diﬀerent sides of r

(10.12)

where r

· n = r

, n is the inner product of the two vectors.

2. In (10.12), r



· n = r

· n,and

· n)(r

·n)=r

, b

× r

r

, b

× r

 . (10.13)

Then, from

× r

10.1 Space Conformation Theory of Four-Atom Points 285

and the outer product formula (10.5), we obtain

× r

) × r

× r



·r

− r



Therefore,

·n)(r

· n)=

× r



·r

)

− r





·r

)(r

·r

) − r

· r

)



Since for any two vectors r

and r

,(r

·r

)

≤ r

always holds true,

sgn [(r

· n)(r



·n)] = sgn [(r

·n)(r

· n)]

=sgn



· r

) − (r

· r

)(r

· r

)



(10.14)

always holds.

3. On the other hand, we can also calculate (b

, b

). The deﬁnition of b

yields

, b

)=α(r

× r

, r

× r

) ,

where

α =

× r

|·|r

× r

> 0 .

Then from the outer product formula, we obtain

, b

)=α



, r

) · (r

, r

) − r

, r

)



;

therefore,

sgn (b

, b

)=−sgn [(r

· n)(r



·n)] . (10.15)

From formula (10.15), we know that the conclusion of the theorem stands.

Hence this theorem is proved.

Theorem 39. The structure types E and Z of the four-atom points conforma-

tion can be determined by the value of the torsion angle ψ, by the relationship:

⎧

⎪

⎨

⎪

⎩

If |ψ|≤

then the conformation of the four-atom points a,b,c,d

is of type Z ,

If |ψ| >

then the conformation of the four-atom points is of type E ,

(10.16)

where 0 ≤|ψ|≤π.

Proof. From the deﬁnition of the torsion angle (10.6), and comparing formula

(10.16) with Theorem 39, we see that this theorem holds.

286 10 3D Structure of the Protein Backbone and Side Chains

The Transformation Relationship for the Four-Atom Points

Torsion Angle and Phase

In the deﬁnition of torsion angle (10.6), ψ is in the domain [0,π]. If it is

combined with the mirror reﬂection value ϑ, ψ can be deﬁned on [0, 2π]. We

then take





ψ, if ϑ = −1 ,

2π − ψ, if ϑ =1.

(10.17)

At this time, ψ



is deﬁned on [0, 2π], and the value of ψ



in the four quadrants

of the plane rectangular coordinate system coincides with the deﬁnition of

(ϑ, ϑ



10.1.3 Four-Atom Construction of Protein 3D Structure

In the construction of protein atoms, we have already introduced the structure

of their backbones and side chains, from which various four-atom points of

diﬀerent types can be obtained. The important types that will be discussed

are as follows.

The Types of Four-Atom Points Obtained from the Protein

Backbones

1. Four-atom points obtained from the three atoms N, A, C in turn are of

the three types: N, A, C, N



;A,C,N



;C,N



, where N, A, C,



are the N, A, C atoms of two neighboring amino acids.

2. A series of four-atom points can be obtained by choosing an atom point in

each amino acid, for example, A

t+1

t+2

t+3

where t =1, 2, 3, ···.

Four-atom points obtained from the side chains of the backbones are of the

type N, A, C, O; N, A, C, B, etc.

Statistical Calculation for the Protein Backbone Four-Atom Points

There are 3190 proteins in the PDB-Select database (version 2005), on which

we may perform statistical calculations for all the four-atom points of the

linked amino acids. The results are as follows:

1. There are 739,030 linked amino acids in the 3190 proteins in the PDB-

Select database (version 2005), and every amino acid consists of diﬀer-

ent atoms. The PDB-Select database gives the space coordinates of all

the non-hydrogen atoms, and the total number of non-hydrogen atoms is

about 5,876,820.

10.1 Space Conformation Theory of Four-Atom Points 287

2. For the atoms N, A, C, N



,wedenoter

, r

to be

the lengths of the vectors

−→

NA,

−→

AC,

−−→



−−→



−−→



−−→



respectively. We denote the torsion angle between plane π(NAC) and

plane π(ACN



)byψ

, the torsion angle between plane π(ACN



) and plane

π(CN



)byψ

, and the torsion angle between plane π(CN



) and plane

π(N



)byψ

We calculate the mean, variance and standard deviation of each of the pa-

rameters r

,ψ

for the 739,030 linked amino acids

in the 3190 proteins in the PDB-Select database (version 2005). The re-

sults are given in Table 10.1.

We see from Table 10.1 that the values of the parameters r

, r

,andψ

are quite constant, where the mean of ψ

is μ =3.14716 =

180.320

◦

. This indicates that the four points A, C, N



are almost on

the same plane.

3. The edge lengths of the four-atom points A

in the backbone

are

The results of our statistical calculations for the torsion angle Ψ are shown

in Table 10.2, where the torsion angle Ψ is the angle between the triangle

δ(A

)andδ(A

), deﬁned on [0, 2π].

4. The phase distribution of ψ

,ψ

and Ψ is shown in Table 10.3.

In the next section, we will analyze the four-atom structure of protein side

chains. In the statistical analysis presented in this book, we include compre-

hensive statistics of all the amino acid parameters. If we analyzed each indi-

vidual amino acid, the values of the related parameters would diﬀer slightly,

which we do not discuss here.

Table 10.1. Parameter characteristics of four-atom points N, A, C, N



diﬀerent amino acids

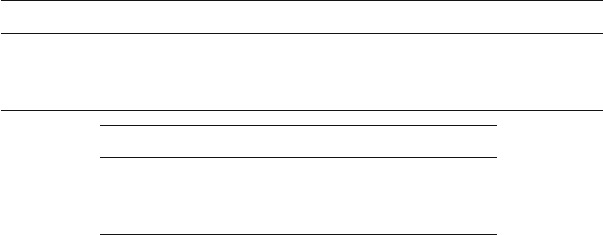
Mean (μ) 1.46215 1.52468 1.33509 2.45624 2.43543 2.43633

Variance (σ

) 0.00018 0.00014 0.00021 0.00258 0.00070 0.00068

Standard deviation (σ) 0.01325 0.01198 0.01455 0.05080 0.02651 0.02608

Mean (μ) 3.52116 3.14716 4.15748

Variance (σ

) 3.77901 0.03136 1.84675

Standard deviation (σ) 1.94397 0.17709 1.35895

288 10 3D Structure of the Protein Backbone and Side Chains

Table 10.2. Parameter characteristics of the four-atom points A

in dif-

ferent amino acids





Mean (μ) 3.81009 3.81007 3.80852 6.02735 6.02492 2.56770

Variance (σ

) 0.00301 0.00308 0.00520 0.39028 0.39149 2.68689

Standard deviation (σ) 0.05490 0.05552 0.07210 0.62473 0.62569 1.63917

Table 10.3. Phase distribution table of ψ

,ψ

,andΨ

Phase value 1 2 3 4

0.1625 0.3507 0.1926 0.3942

0.0014 0.5107 0.4863 0.0015

0.1155 0.0697 0.3156 0.4993

Ψ 0.3971 0.1937 0.2928 0.1164

10.2 Triangle Splicing Structure of Protein Backbones

There are two types of protein backbone structures. There are chains formed

by three atoms N, A, C alternately, and chains made up of atoms A

, ···. They are denoted respectively by



= {(N

, A

, C

), (N

, A

, C

), ··· , (N

, A

, C

)} ,

= {A

, A

, ··· , A

} ,

(10.18)

where n is the length of the protein sequence, that is, the number of amino

acids. We now discuss the structural properties of the protein backbone.

10.2.1 Triangle Splicing Belts of Protein Backbones

We can generally denote the sequences in (10.18) by

L = {Z

, ··· ,Z



−1



} , (10.19)

where n



is 3n or n,whenL is L

or L

, respectively. We denote the space

coordinates of each point Z

by (x

∗

), and L is the space structure

sequence of protein backbones.

Parameter System for Protein Backbone 3D Structures

Similar to the structure parameter theory of four-atom points, we can con-

struct the structure parameter for sequence L. We introduce the relevant

notations as follows:

10.2 Triangle Splicing Structure of Protein Backbones 289

1. If the three neighboring atoms in L are considered to form a triangle, then

L would be formed from a series of conjoined triangles. These triangles

are denoted by

= {δ

,δ

, ··· ,δ



−2

} , (10.20)

where δ

= δ(Z

i+1

i+2

) is the triangle with vertices Z

i+1

i+2

,and

and δ

i+1

are joined and have a common edge Z

i+1

i+2

.WecallL

the

triangle splicing belt of protein backbones.

2. For the triangle splicing belts of protein backbones, we introduce the pa-

rameter system as follows:

⎧

⎪

⎨

⎪

⎩

= |Z

i+1

|,i=1, 2, ··· ,n



− 1 ,



= |Z

i+2

|,i=1, 2, ··· ,n



− 2 ,

angle between

−−−−→

i+1

and

−−−−−−→

i+1

i+2

,i=1, 2, ··· ,n



− 2 ,

torsion angle of triangle δ

and δ

i+1

,i=1, 2, ··· ,n



− 3 ,

mirror value of the four points Z

i+1

i+2

i+3

(10.21)

This yields the parameter system of the triangle splicing belts of protein

backbones:

= {r





,φ



,ψ



,ϑ



,i∈ N



∈ N





∈ N



} , (10.22)

where N



= {1, 2, ···,n



− τ}, τ =1, 2, 3.

3. For the parameter system E

, similarly, we can divide it into two sets:



(1)

= {r





,ψ



,ϑ



,i∈ N



∈ N





∈ N



} ,

(2)

= {r

,φ



,ψ



,ϑ



,i∈ N



∈ N





∈ N



} .

(10.23)

At this time, parameter systems E

(1)

and E

(2)

determine each other, and

the 3D conﬁguration of the protein backbone can be completely deter-

mined.

Phase Sequences of the Protein Backbone 3D Structure

Similar to the four-atom points, we can deﬁne the phase sequences of the

protein backbone 3D structure. Here we take

ϑ = {(ϑ

,ϑ



), (ϑ

,ϑ



), ··· , (ϑ



−2

,ϑ





−2

)} , (10.24)

where ϑ

is deﬁned in formula (10.22), while





+1 , if |ψ

|≤π/2 ,

−1 , otherwise ,i∈ N



(10.25)

Using (ϑ

,ϑ



) and formula (10.17), similarly, the value of ψ

can be extended to

[0, 2π], and its values in the four quadrants of the plane rectangular coordinate

290 10 3D Structure of the Protein Backbone and Side Chains

system can be determined. At this time, we take



⎧

⎪

⎨

⎪

⎩

0 , if ϑ = −1, ϑ



=1,

1 , if ϑ = −1, ϑ



= −1 ,

2 , if ϑ =1,ϑ



= −1 ,

3 , if ϑ =1,ϑ



=1.

(10.26)

Table 9.1 gives the primary structure, secondary structure, and phase sequence

of protein 12E8H, where the phase sequence of the protein is in the third line.

Plane Unwinding of the Triangle Splicing Belts of Protein

Backbones

If the triangle splicing belt L

of a protein backbone is given, its parameter

system E

(0)

will be determined by formula (10.23). We denote the parame-

ter system of the plane unwinding formula of the protein backbone triangle

splicing belt by

(0)







,ψ



,ϑ



,i∈ N



∈ N





∈ N



, (10.27)

where ψ

= ψ

= ··· = ψ



−2

. The triangle splicing belt is then determined

by E

(0)



= {Z



, ··· ,Z





} or L







,δ



, ··· ,δ





−2

, (10.28)

where Z



, ··· ,Z





are points in the ﬁxed plane π(Z



= δ





i+1



i+2



and satisfy the conditions below:

1. Initial condition: (Z



)=(Z

2. Arc length condition: |Z



| = r

, |Z



| = r

, |Z



| = r

, |Z



| = r



| = r

At this time, every protein backbone triangle splicing belt L

can be unwound

into a plane triangle belt L



by rigid rotations between the triangles δ

and

i+1

. Conversely, a plane triangle splicing belt L



, using a rigid rotation be-

tween triangles δ



and δ



i+1

can become a protein backbone triangle belt L

Rigid rotation occurs between δ

and δ

i+1

(or δ



and δ



i+1

), while the parame-

ter structures of the other parts of the backbone triangle splicing belt L

(or

plane triangle splicing belt L



) stay the same. The plane triangle splicing belt

of the protein backbone is shown in Fig. 10.3.

10.2 Triangle Splicing Structure of Protein Backbones 291

Fig. 10.3. Plane triangle splicing belt of the protein backbones

10.2.2 Characteristic Analysis of the Protein Backbone Triangle

Splicing Belts

The Length and Width of the Protein Backbone Triangle Splicing

Belts

If L

is a ﬁxed protein backbone triangle splicing belt, its parameter space

will be E

(1)

. We can then deﬁne the edges and width of this triangle splicing

belt as follows:

1. From vector groups







, r



, ··· , r





−1

= {r



, r



, ··· , r





} ,

(10.29)

where n



is the integral value of n



/2. At this time, L

is formed by

two groups of conjoined vectors, and they are parallel. They are named the

upper edge and lower edge of the triangle splicing belts. Here we denote









i=1



2i−1

,







i=1



(10.30)

as the lengths of the upper and lower edge.

2. In triangle δ

= δ(Z

i+1

i+2

), we denote by h

the height from the vertex

i+1

to edge Z

i+2

;itsformulais:

=2S[δ(Z

i+1

i+2

)]/|Z

i+2

| =2S



, (10.31)

where S

, S[δ(Z

i+1

i+2

)] are both the area of triangle

= δ(Z

i+1

i+2

), while r



= |Z

i+2

| is the length of the line Z

i+2

3. We obtain from the calculation on the PDB-SEL database that the values

of h

are quite constant. In the calculation of triangle belts L

, L

,we

obtain the means and variances of h



Mean (μ) 1.03572 0.90677 0.82643 6.64234 0.84362 0.74411 0.67951 2.24859

Variance(σ

) 0.00074 0.00031 0.00048 0.72640 0.00134 0.00034 0.00047 0.22056

Standard deviation (σ) 0.02714 0.01768 0.02188 0.85229 0.03663 0.01835 0.02171 0.46964

where S



are the areas of triangles δ(NAC), δ(ACN



), δ(CN



)

and δ(A

), respectively, while h

,andh



are relevant

heights of these triangles.

292 10 3D Structure of the Protein Backbone and Side Chains

4. The lengths of 



),



) follow from the limit theorem:

lim



→∞







μ, when L = L

,heren



=3n − 2 ,



, when L = L

,heren



= n − 2 ,

(10.32)

where τ =1, 2, while

⎧

⎪

⎨

⎪

⎩

μ =

μ(r

+ r

(2.45624 + 2.43543 + 2.43633) = 3.664 ,



μ(r



6.02735

=3.0137 .

Here, the data of μ(r

),μ(r



) are given by Tables 10.1

and 10.2.

Using the central limit theorem, the values of 



)and



)canbe

estimated more precisely. We have validated these conclusions with a great

amount of calculations on proteins.

The Relation Analysis of the Phase of the Protein Backbone

Triangle Splicing Belt Between Secondary Structures

It has been mentioned above that the value of the protein backbone triangle

splicing belt phase ϑ



is closely correlated to the protein secondary structure.

When ϑ



=0, 3, four-atom points A

i+1

i+2

i+3

form a Z type, while

when ϑ



=1, 2, four-atom points A

i+1

i+2

i+3

form an E type.

An appendix posted on the Web site [99] gives phase values and secondary

structure sequences of all the proteins in the PDB-Select database. If we

denote by M

the number of the amino acids in the database which take the

secondary structure H or S, denote by M

the number of amino acids in the

database which take the secondary structure H and phase value ϑ



=0, 3,

and denote by M

the number of amino acids in the database which take the

secondary structure S and phase value ϑ



=1, 2, then

=88.25%. From

this, we conclude that the phase of the protein backbone triangle splicing belt

is closely correlated to the secondary structures.

10.3 Structure Analysis of Protein Side Chains

We have stated in Chap. 7 that, for diﬀerent amino acids, the component

structure of the side chains may vary. We now discuss their conﬁguration

characteristics. We have pointed out before that the backbone of a protein

consists of atoms N, C

, C alternately, and they form a space triangle belt.

Thus, the side chains of proteins can be considered to be components localized

in this space triangle belt. We discuss ﬁrst the conﬁguration structure of an

oxygen atom O and an atom C

on the backbones, where the oxygen atom

O is present in all amino acids, while atom C

is present in all amino acids

except the glycines.

10.3 Structure Analysis of Protein Side Chains 293

10.3.1 The Setting of Oxygen Atom O and Atom C

on the Backbones

Relevant Notation

1. We maintain the notation

L = {Z

, ··· ,Z

} = {N

, A

, C

, N

, A

, C

, ··· , N

, A

, C

}

(10.33)

for the backbone of the protein, so the oxygen atom sequences and the

side chain groups sequences are denoted by



¯a = {O

, O

, ··· , O

} ,

¯a = {R

, R

, ··· , R

} ,

(10.34)

where O

are the oxygen atom and the side chain group of the ith

amino acid, respectively.

2. In the side chain group R, except for glycines, all the other amino acids

contain C

atoms, which are denoted by B atoms. Here, the tetrahedrons

formed by the four-atom vertices N, A, C, O and N, A, C, B are V

, V

Their shapes are shown in Fig. 10.4.

Figure 10.4 presents the structural relation of the atoms N, A, C, O, B,



,whereN



is the nitrogen atom of the next amino acid. They form

diﬀerent tetrahedrons separately. For instance, V

= {N, A, C, O}, V

{N, A, C, B}, where point B is usually on one side of the plane N A C,

while point O can be on diﬀerent sides of the plane N A C.

3. For the atom points N, A, C, O, B, N



, their coordinates are denoted

separately by

∗

=(x

∗

) ,τ=1, 2, 3, 4, 5, 6 . (10.35)

We have already given the structural relations of the atom points N, A, C,



in the previous section, so we now discuss the relation between atoms

O, B and atom points N, A, C, N



.Wedenote



= r

∗

− r

∗

=(x

) ,





= r

∗

− r

∗

=(x













) ,

(10.36)

and their lengths are r



, τ =1, 2, 3.

4. In proteins, the tetrahedrons of diﬀerent amino acids with regard to O, B

atoms are denoted by V

i,O

and V

i,B

. Similarly, we can deﬁne the relevant

atom vectors r

i,τ

, r



i,τ

, τ =1, 2, 3 to represent the vectors from atoms

to atom O

and atom point B

. Similarly to the deﬁnition in

(10.36)



i,τ

= r

i,4

− r

i,τ

=(x

i,τ

) ,



i,τ

= r

i,5

− r

i,τ





i,τ





i,τ





i,τ





(10.37)

their lengths are r

i,τ

,andr



i,τ

, τ =1, 2, 3,i=1, 2, ···,n.