Shen S., Tuszynski J.A. Theory and Mathematical Methods for Bioformatics
Подождите немного. Документ загружается.

7.4 The Virtual Symbol Operation in the Alignment Space 241
with radius r = k + 1 as follows:
O
A
(A, k +1)=
6
A
∈O
A
(A,k)
O
A
(A
, 1) = O
A
(A, k)
6
⎡
⎣
6
A
∈O
A
(A,k)
S
A
(A
, 1)
⎤
⎦
.
(7.34)
Obviously, the sets O
A
(A
, 1) for two different centers may overlap with each
other as A
∈ O
A
(A, k) ranges. The recursion is hard to compute, but may
subsequently reduce the level of difficulty for the construction and computa-
tion of the alignment spheroid.
The Decomposition of the Alignment Spheroid According
to the Lengths of Sequences
In the alignment sphere S
A
(A, k), the lengths of the sequences may range
over [n
a
− k, n
a
+ k]. Therefore, it might be decomposed as: S
A
(A, k)=
n
a
+k
n=n
a
−k
S(A, k; n), in which
S
A
(A, k; n)={A
∈ S(A, k)||A
| = n},
n = n
a
− k, n
a
− k +1, ··· ,n
a
,n
a
+1, ··· ,n
a
+ k, (7.35)
where S
A
(A, k; n
a
− k) is the set generated by deleting the k components of
sequence A, S
A
(A, k; n
a
+ k) is the set generated by inserting k components
of sequence A, and the other sets S
A
(A, k; n) are generated by substituting,
deleting and inserting the components of sequence A.
7.4 The Virtual Symbol Operation
in the Alignment Space
In the previous two sections, we referred to the permutation operation of the
virtual symbol in alignment sequences. We now discuss it further. If sequences
(A
,B
) are the alignments of (A, B), then A
and B
are defined on set V
+
.
If we perform the operation on the virtual symbols of A
and B
,thenwecan
get the virtual symbol operator. To understand alignment space in detail, we
next analyze the virtual symbol operator.
7.4.1 The Definition of the Virtual Symbol Operator
The Virtual Symbol Operation on a Single Sequence
Let A
=(a
1
,a
2
, ··· ,a
n
) be the expansion of sequence A =(a
1
,a
2
, ··· ,a
n
).
Based on A
,wemayobtainA by deleting all the virtual symbols of A
.We
obtain a new expansion of A if we continue to insert or delete some virtual
symbols in A
. This operation is called the virtual symbol operation on A
.
242 7 Alignment Space
If A
is generated by sequence A
through the virtual symbol operation,
we can also represent the relationship by modulus structure. Here, let
H
∗
= {(j
k
,
∗
k
),k=1, 2, ··· ,k
a
} (7.36)
be the modulus structure of the virtual symbol operation from A
to A
,in
which
∗
k
=0,and(j
k
,
∗
k
) means that we insert or delete
∗
k
components after
the j
k
th component of A
,inwhich
0=j
0
≤ j
1
<j
2
<j
3
< ···<j
k−1
≤ j
k
= n
a
. (7.37)
The inserting or deleting operations depend on whether
∗
k
> 0or< 0. In
addition, in the case
∗
k
< 0, the a
j
k
+1
,a
j
k
+2
, ··· ,a
j
k
+
∗
k
are virtual symbols
required to keep (7.36) well-defined. Let A
= H
∗
(A
), where H
∗
is the virtual
symbol operator of A
, with the following properties:
1. If A
is an expansion of A,andH
∗
is the virtual symbol operator of A
,
then A
= H
∗
(A
) is still an expansion of A.
2. If A
and A
both are expansions of A, then there is a virtual symbol
operator H
∗
of A
such that A
= H
∗
(A
).
The proofs of the two propositions are obvious, and hence we omit them here.
Example 27. In the set V
2
, the components of value 2 are virtual symbols. The
modulus structures of virtual symbol operation on the following sequences are
shown as follows:
1. If
A
= (11111 22200 00000)
A
= (11111 00000 00) ,
then H
∗
= {(5, −3)}.
2. If
A
= (11111 00000 00)
A
= (11111 22200 00000) ,
then H
∗
= {(5, 3)}.
3. If
A
= (11111 21111 11111)
A
= (11111 11112 11111) ,
then H
∗
= {(5, −1), (10, 1)}.
The Virtual Symbol Operation on Alignment Sequences
Let (A
,B
) be the alignments of (A, B), and H
∗
a
, H
∗
b
be the virtual symbol
operators of A
and B
to A and B, respectively. Let their modulus struc-
7.4 The Virtual Symbol Operation in the Alignment Space 243
tures be
⎧
⎨
⎩
H
∗
a
=
j
a,k
,
∗
a,k
,k=1, 2, ··· ,k
a
,
H
∗
b
=
j
b,h
,
∗
b,h
,h=1, 2, ··· ,k
b
.
(7.38)
It should be noted that the fact that H
∗
a
, H
∗
b
are the modulus structures of
the virtual symbol operators of A
and B
, respectively, does not imply that
(H
∗
a
, H
∗
b
) are always the modulus structures of the virtual symbol operators
of (A
,B
). We add special conditions that are defined as follows.
Definition 38. (H
∗
a
, H
∗
b
) are the virtual symbol operators on the alignment
sequences (A
,B
) of (A, B) if their modulus structures satisfy the following
conditions:
1. H
∗
a
,H
∗
b
are the modulus structures of the virtual symbol operators of A
and B
, and satisfy the expression L
∗
a
= L
∗
b
,where
L
∗
a
=
k
a
k=1
∗
a,k
,L
∗
b
=
k
b
k=1
∗
b,k
. (7.39)
2. In (j
a,k
,
∗
a,k
),alla
j
a,k
+1
,a
j
a,k
+2
, ··· ,a
j
a,k
,
a,k
are not virtual symbols if
∗
a,k
> 0. Similarly, all b
j
b,h
+1
,b
j
b,h
+2
, ··· ,b
j
b,h
+
b,h
are not virtual sym-
bols if
∗
b,h
> 0.
3. All a
j
a,k
+1
,a
j
a,k
+2
, ··· ,a
j
a,k
+
a,k
are virtual symbols if
∗
a,k
< 0.All
b
j
b,h
+1
,b
j
b,h
+2
, ··· ,b
j
b,h
+
b,h
are virtual symbols if
∗
b,h
< 0.
The Properties of Virtual Symbol Operation of Alignment
Sequences
For the virtual symbol operation (H
∗
a
, H
∗
b
) on the alignment sequences (A
,B
)
of (A, B), the following properties also hold:
1. If (A
,B
) is the alignment of (A, B), and (H
∗
a
, H
∗
b
) are the virtual sym-
bol operators on (A
,B
), then (A
,B
)=(H
∗
a
(A
), H
∗
b
(B
)) is also the
alignment of (A, B).
2. If (A
,B
), (A
,B
) are all the alignment sequences of (A, B), then
there must be a virtual symbol operator (H
∗
a
, H
∗
b
)of(A
,B
) such that
(A
,B
)=(H
∗
a
(A
), H
∗
b
(B
)).
The proofs of these two propositions are obvious and hence are omitted here.
7.4.2 The Modulus Structure of the Virtual Symbol Operator
In Chap. 3, we introduced the modulus structure theory for sequence muta-
tions and alignments. Also, in the above section, we introduced the modulus
structure for the virtual symbol operator. Now, we discuss the relationships
between them.
244 7 Alignment Space
The Properties of the Modulus Structure of the Virtual Symbol
Operator for a Single Sequence
If A
is an expansion of A, then based on the discussion in Chap. 3, we in-
fer that the transformation from A to A
is uniquely determined by modulus
structure H = {(i
k
,
k
), where k =1, 2, ··· ,k
a
}.Furthermore,ifA
is gener-
ated by the virtual symbol operation on A
, then with the same discussion as
in the above section, we find that the transformation from A
to A
is deter-
mined by the modulus structure H
∗
= {(j
k
,
∗
k
), where k =1, 2, ··· ,k
a
}.The
operators H, H
induced by the modulus structures H, H
∗
satisfy A
= H(A),
and A
= H
(A
).
On the other hand, based on the proposition (2) of the virtual symbol
operation for a single sequence, we conclude that A
is the expansion of A.
Therefore, there is a modulus structure H
and its corresponding operator H
such that A
= H
(A). The properties of the modulus structure of the virtual
symbol operator for a single sequence are mainly the relations between H, H
∗
and H
. We discuss them below:
1. In the definitions of H, H
∗
and H
,wefirstnotethatH and H
are
the modulus structures of the sequence determined by A, while H
∗
is the
modulus structure of the virtual symbol determined by A
. Here, posi-
tion j
k
in H
∗
has values in {1, 2, ··· ,n
a
}. Therefore, a
j
k
∈ V
+
means a
j
k
can be valued in V or valued as “−”.
2. Following from the relationship between A and A
, we define
i
k
= j
k
− L
j
k
= j
k
−
j
k
−1
j=1
κ
−
a
j
(7.40)
where
κ
−
a
j
=
1 , if a
j
is the virtual symbol “−”,
0 , otherwise .
Based on this, we define the modulus structure as follows:
H
= {(i
k
,
k
) ,k=1, 2, ··· ,k
a
} (7.41)
in which i
k
is defined by (7.40), and
k
=
∗
k
.
3. Let H
= {(i
k
,
k
),k=1, 2, ··· ,k
a
} be the modulus structure from A to
its expansion A
,andI,I
,I
be the position sets of H, H
and H
,then
we define set I
= I ∪ I
= {i
1
,i
2
, ··· ,i
k
},where
k
=
⎧
⎪
⎨
⎪
⎩
k
, when i
k
= i
k
∈ I but i
k
is not in I
,
k
, when i
k
= i
k
∈ I but i
k
is not in I
,
k
+
k
, when i
k
= i
k
= i
k
∈ I ∩ I
.
(7.42)
7.4 The Virtual Symbol Operation in the Alignment Space 245
4. From the definitions of H
and H
∗
we see in (7.42) that
k
> 0 must apply
to the second case and
k
+
k
> 0 must apply to the third case; so
k
≥ 0
is always true. Their relation is as follows:
A
= H(A) ,A
= H
(A)=H
∗
(A
) . (7.43)
The Properties of the Modulus Structure of the Virtual Symbol
Operator for Alignment Sequences
The properties of the modulus structure of the virtual symbol operator for
a single sequence can be easily extended to the case of alignment sequences.
We elaborate on it below.
If sequences (A
,B
) are the alignment sequences of (A, B), the modulus
structures of the virtual symbol operations and the operators of (A
,B
)are
(H
∗
a
,H
∗
b
), (H
∗
a
, H
∗
b
) respectively, then
(A
,B
)=(H
∗
a
, H
∗
b
)(A
,B
)=(H
∗
a
(A
), H
∗
b
(B
)) . (7.44)
We discuss the following properties:
1. The modulus structure of the alignment sequence (A
,B
)of(A, B)
is: (H
a
,H
b
). The modulus structure of the virtual symbol operator for
(A
,B
)with(A
,B
)is(H
∗
a
,H
∗
b
). Here, (A
,B
) given in (7.44) are also
the alignment sequences of (A, B). Their modulus structure is denoted by
(H
a
,H
b
).
2. Using the properties (7.41) of the modulus structure for the virtual symbol
operator of a single sequence we can transform the modulus structure of
(A
,B
) into the modulus structure (H
a
,H
b
)of(A, B), where
⎧
⎨
⎩
H
a
=
i
a,k
,
a,k
,k=1, 2, ··· ,k
∗
a
,
H
b
=
i
b,k
,
b,k
,k=1, 2, ···,k
∗
b
,
(7.45)
and
i
τ,k
= j
τ,k
− L
∗
τ,j
k
= j
τ,k
−
j
τ,k
j=1
κ
−
(τ
j
) ,τ= a, b ,
τ,k
=
∗
τ,k
,τ= a, b ,
(7.46)
where
κ
−
τ
j
=
1 , when τ
j
is valued “−”,
0 , otherwise .
3. Similar to expression (7.42), we find the relation between (H
a
,H
b
),
(H
a
,H
b
), and (H
a
,H
b
), so that the expression
(A
,B
)=(H
a
, H
b
)(A, B)=(H
a
(A), H
b
(B)) ,
(A
,B
)=(H
a
(A), H
b
(B)) = (H
∗
a
(A
), H
∗
b
(B))
(7.47)
holds.
246 7 Alignment Space
The Basic Types of Modulus Structure of the Virtual Symbol
Operator for Alignment Sequences
Following from the definition of the modulus structure (H
∗
a
,H
∗
b
) of the virtual
symbol operator for alignment sequences, we can determine its basic type
as: I
j
a
,j
b
;±
,where is a nonnegative integer. This is the simpler form of
H
∗
a
= {(j
a
, ±)}, H
∗
b
= {(j
b
, ±)},wherej
a
= j
b
. It means that after the sites
j
a
,j
b
of sequences A
,B
, we insert or delete virtual symbols “−”.
Obviously, any virtual symbol operator of alignment sequences can be
decomposed to the product of several single symbol insertion and deletion
types.
Example 28. Let
A = (11111 00000 11111) ,
B = (00111 11000 0011) ,
and let
A
= (11111 22000 00111 11) ,
B
= (00111 11000 00222 11) ,
A
= (22111 11000 00111 11) ,
B
= (00111 11000 0011222) ,
then
H
a
= {(5, 2)},
H
b
= {(12, 3)},
H
∗
a
= {(0, 2), (5, −2)},
H
∗
b
= {(12, −3), (17, 3)} .
Furthermore,
H
a
= {(0, 2), (5, −2)},
H
b
= {(12, −3), (14, 3)},
H
a
= {(0, 2)},
H
b
= {(14, 3)} .
Then the decomposition of (H
∗
a
, H
∗
b
) is shown as follows:
I
0,17;2
A
B
=
221111 12200 00011 111
00111 11000 00222 1122
=
A
1
B
1
,
I
7,12;−2
A
1
B
1
=
22111 1100 00011 111
00111 11000 0021 122
=
A
2
B
2
,
I
14,15;1
A
2
B
2
=
22111 11000 00112 111
00111 11000 00211 222
=
A
3
B
3
,
I
14,12;−1
A
3
B
3
=
22111 11000 00111 11
00111 11000 00112 22
=
A
B
.
Finally, we have
A
B
=
H
∗
a
(A)
H
∗
b
(B)
= I
14,12;−1
I
14,15;1
I
7,12
I
7,12;−2
I
0,17;2
A
B
.
Therefore, the decomposition
(H
∗
a
, H
∗
b
)=I
14,12;−1
I
14,15;1
I
7,12;−2
I
0,17;2
holds.
7.4 The Virtual Symbol Operation in the Alignment Space 247
7.4.3 The Isometric Operation and Micro-Adapted Operation
of Virtual Symbols
For the sake of simplicity, we assume that for any case involving the matrix,
we use the Hamming matrix.
The Definitions of the Isometric Operator and Micro-Adapted
Operator for Virtual Symbols and Their Properties
Definition 39. Let (A
,B
) be the alignment of (A, B),and(H
∗
a
,H
∗
b
) be the
virtual symbol operators on (A
,B
) such that
(A
,B
)=(H
∗
a
(A
), H
∗
b
(B
)) .
Then, (H
∗
a
,H
∗
b
) is an isometric operator on (A
,B
) if d
+
(A
,B
)=
d
+
(A
,B
),and(H
∗
a
,H
∗
b
) is a micro-adapted operator on (A
,B
) if
d
+
(A
,B
) <d
+
(A
,B
).
Next, we discuss the properties of the isometric operator. Let (A
,B
)be
the alignment, and the virtual symbol operator (H
∗
a
, H
∗
b
). We introduce the
following notations:
j
∗
m
=min{j
∗
a,k
,k=1, 2, ··· ,k
a
,j
∗
b,k
,k
=1, 2, ··· ,k
b
},
j
∗
M
=max{j
∗
a,k
+
∗
a,k
,k=1, 2, ··· ,k
a
,j
∗
b,k
+
∗
b,k
,k
=1, 2, ··· ,k
b
} .
(7.48)
(j
∗
m
,j
∗
M
) is the value range of the virtual symbol operator. Based on (j
∗
m
,j
∗
M
),
we can determine the subsequences of A
and B
as follows:
⎧
⎨
⎩
A
mM
=
a
j
∗
m
+1
,a
j
∗
m
+2
, ··· ,a
j
∗
M
,
B
mM
=
b
j
∗
m
+1
,b
j
∗
m
+2
, ··· ,b
j
∗
M
.
(7.49)
Let L
0
=
k
a
k=1
a,k
=
k
b
k=1
b,k
be the total number of insertions or dele-
tions of the virtual symbol operator of the alignment sequences. Based on
these notations, we can formulate the basic property theorem for the isomet-
ric operator as follows.
Theorem 35. If (A
,B
), (A
,B
) are both the optimal alignments of (A, B),
then there is an isometric operator (H
∗
a
, H
∗
b
) such that A
= H
∗
a
(A
),B
=
H
∗
b
(B
).
On the other hand, if (A
,B
) are the optimal alignment sequences of
(A, B),and(H
∗
a
, H
∗
b
) is the isometric operator on (A
,B
),then(H
∗
a
, H
∗
b
)
is also an optimal alignment, in which A
= H
∗
a
(A
) and B
= H
∗
b
(B
).
Proof. The proof of the theory is obvious. Because (A
,B
), (A
,B
)areboth
the alignment sequences of (A, B), then making use of the properties of the
248 7 Alignment Space
virtual symbol operator of alignment sequences, we find the isometric operator
(H
∗
a
, H
∗
b
) such that A
= H
∗
a
(A
), B
= H
∗
b
(B
). Since (A
,B
), (A
,B
)are
both the alignments of (A, B), this implies that d
+
(A
,B
)=d
+
(A
,B
)
holds, meaning that (H
∗
a
,H
∗
b
) is an isometric operator on (A
,B
).
The converse proposition is obtained using the optimal alignment (A
,B
)
and the definition of the isometric operator (H
∗
a
, H
∗
b
).
The Basic Types of Isometric Operators
In Sects. 7.4.2 and 7.4.3, we have stated the basic types I
j
a
,j
b
;
of isometric
operators. We now discuss their properties.
Theorem 36. In order for the basic type I
j
a
,j
b
;
to be an isometric operator,
the necessary and sufficient conditions in different cases are stated as follows:
1. In the case where >0 and j
a
<j
b
− ,thenI
j
a
,j
b
;
is an isometric
operator if and only if
d
H
a
j
a
,j
b
,b
j
a
,j
b
= d
H
a
j
a
,j
b
−
,b
j
a
+,j
b
+2, (7.50)
in which c
i,j
=(c
i+1
,c
i+2
, ··· ,c
j
),andc = a, b.
By symmetry, in the case where j
b
<j
a
−, I
j
a
,j
b
;
is the isometric operator
if and only if
d
H
a
j
b
,j
a
,b
j
b
,j
a
= d
H
a
j
b
+,j
a
,b
j
b
,j
a
−
+2. (7.51)
2. In the case where <0 and j
a
<j
b
+ , I
j
a
,j
b
;
is an isometric operator
if and only if
d
H
a
j
a
+,j
b
,b
j
a
+,j
b
= d
H
a
j
a
−,j
b
−
,b
j
a
,j
b
− 2. (7.52)
By symmetry, in the case where j
b
<j
a
+, I
j
a
,j
b
;
is the isometric operator
if and only if
d
H
a
j
b
−,j
a
,b
j
b
−,j
a
= d
H
a
j
b
,j
a
,b
j
b
−,j
a
−
− 2. (7.53)
Proof. The proof of this theorem follows from Fig. 7.1. For the case >0and
j
a
<j
b
− , the proof is demonstrated below.
In Fig. 7.2, (A
,B
) are the alignment sequences of (A, B). Operation
I
j
a
,j
b
;
inserts virtual symbols after position i
a
of A
to obtain A
,andin-
serts virtual symbols after position j
b
of B
to obtain B
.ThenA
,B
just
act in the region (j
a
,j
b
+ 1) and do not involve the other regions. Therefore,
d(A
,B
)=d
a
0,j
a
,b
0,j
a
+ d
a
j
a
,j
b
+
,b
j
a
,j
b
+
+ d
a
j
b
+,n
,b
j
b
+,n
holds, in which case n
= n
+ .Wethenhave
d(A
,B
)=d
a
0,j
a
,b
0,j
a
+ d
a
j
a
,j
b
+
,b
j
a
,j
b
+
+ d
a
j
b
,n
,b
j
b
,n
. (7.54)
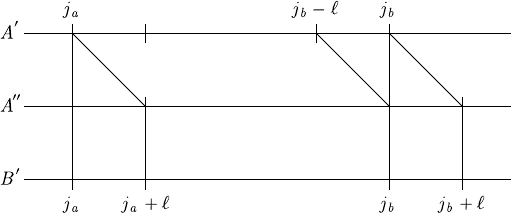
7.4 The Virtual Symbol Operation in the Alignment Space 249
Fig. 7.2. I
j
a
,j
b
;
. The isometric operator
Thus,
d
a
j
a
,j
b
+
,b
j
a
,j
b
+
= d
a
j
a
,j
a
+
,b
j
a
,j
a
+
+ d
a
j
a
+,j
b
,b
j
a
+,j
b
+ d
a
j
b
,j
b
+
,b
j
b
,j
b
+
.
Since both a
j
a
,j
a
+
and b
j
b
,j
b
+
are virtual symbol vectors, following from Def-
inition 38 we know that not every component in vectors b
j
a
,j
a
+
and a
j
b
,j
b
+
is a virtual symbol. Thus, we obtain the expression
d
a
j
a
,j
a
+
,b
j
a
,j
a
+
= d
a
j
b
,j
b
+
,b
j
b
,j
b
+
=
and
d
a
j
a
+,j
b
,b
j
a
+,j
b
= d
a
j
a
,j
b
−
,b
j
a
+,j
b
.
Therefore, we have
d
a
j
a
,j
b
+
,b
j
a
,j
b
+
=
a
+
b
+ d
a
j
a
,j
b
−
,b
j
a
+,j
b
.
Substituting this result into (7.54), we find that (7.50) holds.
With the same arguments, we may prove the other cases, so that the
theorem is proved in its entirety.
Remark 12. For the isometric operator, we should note that the product U
1
U
2
may be an isometric operator, although both U
1
and U
2
are not isometric
operators. For instance, in example 28, I
14,15;1
, I
14,12;−1
are both not isometric
operators, but their product is an isometric operator. In fact, I
14,12;−1
I
14,15;1
is the same as the permutation below:
I
7,12;−1
I
14,15;1
A
2
B
2
= I
14,12;−1
22111 11000 00112 111
00111 11000 00211 222
=
22111 11000 00111 11
00111 11000 00112 22
We define another type of virtual symbol operation as follows.
250 7 Alignment Space
Definition 40. In sequence A
or B
, if just one of the two connected com-
ponents is a virtual symbol, then we exchange the positions of the two compo-
nents, for example, positions 1 and 2 are exchanged to become 2 and 1. This
kind of exchange is called a transposition operation for virtual symbols.
Let II
A
,i+
denote the transposition operation acting on components (a
i
,a
i+1
)
of A
such that the output is (a
i+1
,a
i
); and let II
A
,i−
denote the transposi-
tion operation acting on components (a
i−1
,a
i
)ofA
such that the output is
(a
i
,a
i−1
). For the two operations, the component a
i
= 2 must be the virtual
symbol. Similarly, we may define the operations II
B
,j+
and II
B
,j−
.
Theorem 37. The operation II
A
,j±
is an isometric operator if and only if
b
j
= b
j±1
. Similarly, the operation II
B
,j±
is an isometric operator if and
only if a
j
= a
j±1
.
The proof of this theorem is obvious.
7.5 Exercises, Analyses, and Computation
Exercise 34. Prove the following propositions:
1. Give an example showing that Lemma 3 holds.
2. Prove Theorem 29 and proposition 2 of Theorem 31.
3. Prove formula (7.8).
4. Prove propositions 1–4 in Sect. 7.2.4.
Exercise 35. Based on Example 26, perform the following computations:
1. Compute the maximum core D of (A
,B
) and discuss its uniqueness.
2. Give the alignment modulus structure of (A
,B
) and the other four types
of modulus structures.
3. Compute the five maximum scoring alignments of (A, B).
Exercise 36. For the pairwise alignment in Exercise 13 in Chap. 3:
1. Construct the maximum core and minimum envelope, and give the mod-
ulus structure.
2. Determine the standard mode of the minimum envelope generated by
the modulus structure of the maximum core (may not be unique) and
construct all the minimum envelopes from this.
3. Use the counting theorem of the minimum envelope to explain the en-
velopes generated by task 2 and all the minimum envelopes of these se-
quences.
4. Use the minimum envelope of the pairwise sequences to construct their
minimum penalty alignment sequences.
