Seetharaman S. Fundamentals of metallurgy
Подождите немного. Документ загружается.

2.3.4 Maxwell's relations
Combination of first and second laws yields the following expressions:
dU TdS ÿ PdV (@T/@V)
S
ÿ(@P/@S)
V
(2.21a)
dH TdS VdP (@T/@P)
S
(@V/@S)
P
(2.21b)
dG VdP ÿ SdT (@S/@V)
T
(@P/@T)
V
(2.21c)
dA ÿPdV ÿ SdT (@V/@T)
P
ÿ(@S/@P)
T
(2.21d)
These four equations are termed Maxwell's relations.
2.3.5 Gibbs energy variation with pressure and temperature
From Maxwell's relations, it is quite easy to derive the pressure and temperature
dependencies of Gibbs energy. Equation (2.21c) leads to the relationship:
(@G/@P)
T
V and (@G/@T)
P
ÿS (2.22)
Further, according to equation (2.20),
G H ÿ T.S
H T.(@G/@T)
P
(2.23)
[@(G/T)/@T]
P
= ÿH/T
2
(2.24)
and
[@(G/T)/@(1/T]
P
H (2.25)
Equations (2.24) and (2.25) are referred to as two different forms of Gibbs±
Helmholtz equation.
2.3.6 The third law of thermodynamics
Nernst postulated that, for chemical reactions between pure solids, the Gibbs
energy and enthalpy functions, [@(G/T)/@T]
P
as well as [@H/@T]
P
approach
zero as the temperature approaches absolute zero. This further led to the theorem
that, for all reactions involving condensed phases, S is zero at absolut e zero.
This was further developed by Planc k to the third law of thermodynamics in a
new form, viz. `the entropy of any homogeneous substance in complete internal
equilibrium may be taken as zero at 0 K'.
Glasses, solid solutions or other systems (for example, asymmetric molecules
like CO) that do not have internal equilibrium will obviously deviate from third
law. The same is true for systems with different isotopes.
46 Fundamentals of metallurgy
2.3.7 Entropy and disorder
The second law of thermodynamics states that the total entropy is increasing for
spontaneous processes. In the atomistic level, entropy is considered to be a
degree of disorder arising due to randomness in configuration as well as energy
contents. The latter can manifest itself as vibrational, magnetic or rotational
disorders. From a statistical mechanics treatment of disorder, Boltzman arrived
at the equation for configurational entropy as
S k ln ! (2.26)
where k is the Boltzman constant and ! number of arrangements within the most
probable distribution.
Richard's and Trouton's rules
The degree of disorder increases as a substance melts. As a stronger bonding
energy between atoms need a higher temperature to cause disorder, Richard's
rule states that
S
f
L
f
/T
f
ca 8.4 J. K
ÿ1
(2.27)
where S
f
is the entropy of fusion, L
f
is the latent heat of fusion and T
f
is the
melting point. In reality, Richard's rule, which is empirical, holds approximately
for metals, the values tend to be higher for metalloids and salts.
Another useful emp irical rule for the heat of vaporization at the boiling point
is given by Trouton's rule, viz.
S
v
L
v
/T
v
ca 88 J. K
ÿ1
(2.28)
where S
v
is the entropy of vaporization, L
v
is the latent heat of vaporization
and T
v
is the boiling point.
2.3.8 Reference states for thermodynamic properties
The absolute values of enthalpy are not known; but only changes can be
measured. In order to facilitate the computation of enthalpies, especially as a
function of temperature, the accepted convention is to assign a value of zero to
all pure elements in their stable modifications at 10
5
Pa and 298.15K, which are
the reference points. The enthalpies at other temperatures can be cal culated by
using the expression
@H=@T
P
C
P
) H
Z
T
22
T
1Re f
C
P
dT HT
2
; P ÿ
o
H
Re f
2:29
The enthalpies of compounds can be calculated by adding the enthalpy of the
reaction between the elements. The superscript `o' stands for pure substance.
Thermodynamic aspects of metals processing 47
In the case of entropies, the computation of entropies at temperatures other
than the reference temperatures is carried out using the equation:
o
S
T
o
S
REF
Z
T
1
T
REF
C
P
d ln T 2:30
Newmann±Kopp rule
In the estimation of enthalpies and entropies of compounds from elements, the
Newmann±Kopp rule can be applied with reasonable success, even though it is
claimed that this rule lacks a theoretical basis. According to this rule
C
P
(compound) C
P
(components) (2.31)
2.3.9 Some thermodynamic compilations
It is important that a metallurgist has access to thermodynamic data of the
systems of intere st at temperatures of relevance. So me of the classical
compilations are listed below:
Thermochemical tables
1. Materials Thermochemistry, O. Kubaschewski, C.B. Alcock and P.J.
Spencer, Pergamon Press (1993).
2. Thermochemical Properties of Inorganic Substances, I. Barin and O.
Knacke, Springer-Verlag, Berlin (1973, Supplement 1977).
3. JANAF Thermochemical Tables, N.B.S., Michigan (1965±68, Supplement
1974±75).
4. Selected Values of Thermochemical Properties of Metals and Alloys, R.
Hultgren, R.L. Orr, P.D. Anderson and K.K. Kelley, John Wiley & Sons,
NY (1963).
5. Thermochemistry for Steelmaking, Vol. I & II, J.F. Elliot, M. Gleiser, J.F.
Elliott, M. Gleiser and V. Ramakrishna, Addison-Wesley, London (1963).
Thermochemical databases
1. HSC databas ± Finland
2. Thermo-Calc ± Sweden
3. Chemsage/F.A.C.T. ± Canade, Germany, Australia
4. MT Data ± England
5. THERMODATA ± France
48 Fundamentals of metallurgy
2.4 Unary and multicomponent equilibria
2.4.1 Unary systems
As stated previously, the condition for chemical equilibrium is that the Gibbs
energy of the products and reactants are equal and that there is no net driving
force for the reaction in either direction. This can be easily understood in the
case of systems consisting of a single component. At the melting point of ice, the
equilibrium condition is:
S
G
H20
l
G
H2O
(2.32)
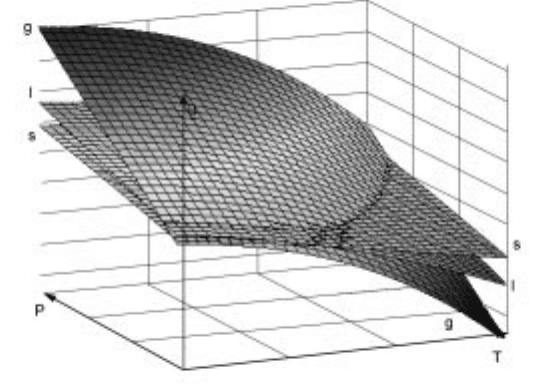
The Gibbs energy of the solid, liquid and gas phases in a G±P±T diagram, where
the intersections of the Gibbs energy planes represent equality in the Gibbs
energy values at given temperatures and pressures is present ed in Fig. 2.5. Solid
and liquid planes cross at the melting point, while the liquid and gas phase
intersect at the boiling point . The three planes meet at a unique temperature and
pressure when all the three phases have the same Gibbs ener gy. This point is
known as the triple point.
The projection of the Gibbs energy planes in Fig. 2.5 on to the P±T base plane
would provide an understanding of the stability areas of various phases as
functions of temperature and pres sure. Such a projection is presented in Fig. 2.6.
2.4.2 Clapeyron and Clausius±Clapeyron equations
An imaginary line in Fig. 2.5 from the triple point along the intersection of the
solid and liquid planes represents the variation of melting point as a function of
2.5 Gibbs energy± temperature± pressure diagram in the case of a one-
component system.
Thermodynamic aspects of metals processing 49

pressure. The mathematical relationship can easily be derived from equation
(2.21c) of the Maxwell relationship, viz.
dG VdP ÿ SdT (@S/@V)
T
(@P/@T)
V
(2.21c)
For a phase transformation reaction, the S and V terms could be replaced by S
and V, the entropy and volume changes accompanying the transformations
respectively. Equation (2.21c) can then be rewri tten as
ÿS
S
dT V
S
dP ÿS
l
dT V
l
dT (2.33)
(S
l
ÿ S
S
)dT (V
l
ÿ V
S
)dP (2.34)
dP
dT
S
f
V
f
H
f
T
f
1
V
f
2:35
where S
f
, V
f
and H
f
are the entropy, volume and enthalpy changes
respectively accompanying melting at the fusion temperature, T
f
. The above
equation holds for any phase transformation in a single component system and is
referred to as the Clapeyron equation. This equation is extremely useful in
estimating the variation of the melting point as the ambient pressure changes and
finds applications in high pressure synthesis of materials.
When the Clapeyron equation is applied to the vaporization of a liquid or
solid, the V term reduces to V, which is much larger compared to the
condensed phases. Thus equation (2.33) is rewritten, combining with the ideal
gas law, as
dP
dT
H
V
TV
V
H
V
R T
2
P 2:36
dP
P dT
H
V
R T
2
2:37
d ln P
dT
H
V
R T
2
2:38
T
P
S
l
g
2.6 Projection of the Gibbs energy planes in Fig. 2.5 on the P-T base plane.
50 Fundamentals of metallurgy
where the subscript `V' refers to vaporization.
The Clausius±Clapeyron equation is very useful in determining the latent
heat of vaporization or the vapour pressure of a substance at a temperature with
a knowledge of the same at another temperature and the latent heat.
2.4.3 Multicomponent systems
Maxwell's relationship for a single component system is expressed by equation
(2.21c). In the case of systems with more than one component, the Gibbs energy
of the component should be added to the equation. Hillert
3
suggests that the
inner driving force, could be added with great advantage in describing
reactions like, for example, nucleation. Thus, the integrated driving force can be
rewritten for multicomponent systems as
dG V.dP ÿ S.dT
i
.dn
i
ÿ D.d (2.39)
where
i
is the chemical potential of component `i' per mole of `i', n
i
is the
number of moles of `i', D is defined as ÿ(@U/@)
S,V,ni
. The common practice is
to express equation (2.39) without the last term on the right-hand side. It is
important to realize that the different phases in the system have thermal,
mechanical and chemical equilibria prevailing.
In the case of a binary system, it is illustrative to add a third composition axis
to Fig. 2.6 on the basis of equation (2.39) without the last term on the right- hand
side. This is shown in Fig. 2.7. While vertical planes corresponding to the pure
substances are identical with Fig. 2.6, the region in between has three
dimensional regions of stability of single phases as well as those with two
phases. The two phase regions are shaped as convex lenses. A section of the
diagram in Fig. 2.7 corresponding to 1 bar (10
5
Pa) plane will yield a diagram as
shown in Fig. 2.8. Figure 2.8 is a simple binary phase diagram showing the
stabilities of solid and liquid phases as a function of temperature. Among the
phase diagram types commonly used in metallurgy, eutect ic and peritectic types
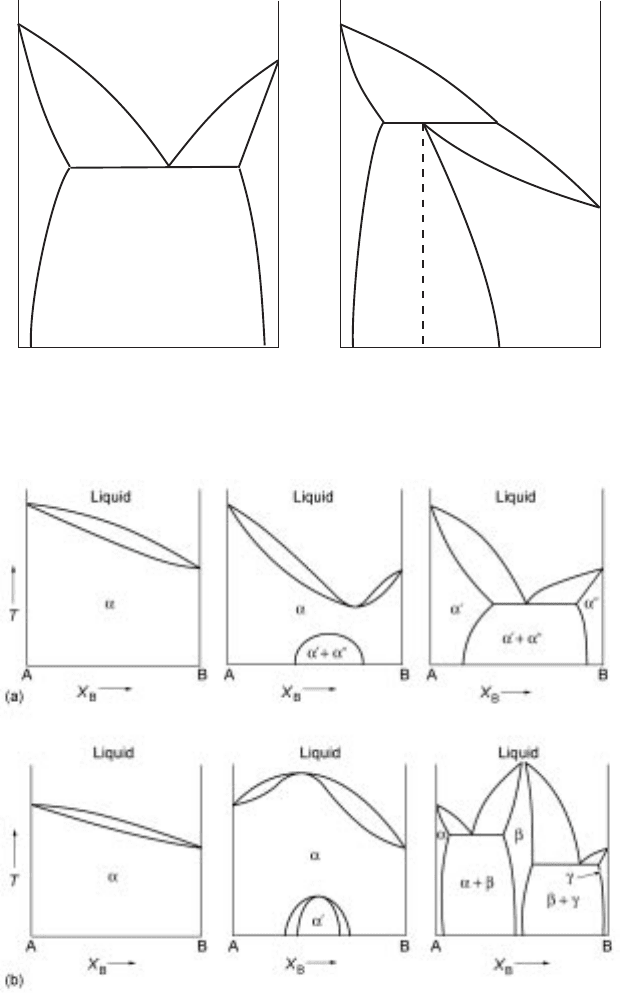
of diagrams are important. These are presented in Fig. 2.9.
In Fig. 2.8, the two components are chemically similar and thus exhibit
complete solubilities in solid and liquid phases. The repulsive or attractive
forces between the components in a binary system can result in partial
solubilities or compound formation in the solid state respectively. In the former
case, the liquid formation is favoured at lower temperatures. The contrary is true
in the case of compound formation. Figure 2.10 presents some examples of how
attractive and repulsive forces influence the phase diagrams for binary systems.
2.4.4 Gibbs phase rule
In accordance with the requirements for equilibrium, different phases in a
system have the same temperature and pressure. Further, each of the components
Thermodynamic aspects of metals processing 51

P
T
s
s + g
s + l
g + l
l
g
A
B
X
B
2.7 Composition±temperature±pressure diagram for a binary system.
4
A B
T
1
a + 1
a
P = 1 atm
X
B
2.8 A simple binary phase diagram showing the complete mutual solubilities of
the two components A and B in solid as well as liquid state.
52 Fundamentals of metallurgy
A
B
l
a
b
A
B
l
a
b
X
O
T
T
(a) (b)
2.9 Some common types of binary phase diagrams (a) eutectic diagram (b)
peritectic diagram.
2.10 (a) Binary phase dia grams wher e the repulsive forces between the
components are manifested.
5
(b) Binary phase diagrams where the attractive
forces between the components are manifested.
5
Thermodynamic aspects of metals processing 53

has the same chemical potential in all the phases in equilibrium. This led to the
derivation of the Gibbs phase rule, which states that
F C ÿ P 2 (2.40)
where `F' is the minimum number of degrees of freedom required to reproduce
the system, `C' represents the number of independent components in the system
and `P' refers to the number of phases. The Gibbs phase rule is applicable to
multicomponent macro systems in determining the number of phases at a given
temperature and pressure.
2.4.5 Gas mixtures
Maxwell's relationship (equation 2.21c) gets reduced at constant temperature to
the form
dG VdP R Td ln P 2:41
Z
P
2
P
1
dG R T
Z
P
2
P
1
d ln P R T
P
2
P
1
2:42
GP
2
; T ÿ GP
1
; T 2:43
If P
1
= 1 bar (10
5
Pa), G(P
1
, T) is the Gibbs energy in the standard state at
temperature T and can be denoted as ëG, thus equation (2.43) can be rewritten as
G(P
2
,T) ëG R T ln(P
2
/1) ëG R T ln(P
2
) (2.44)
In chemistry literature, it is common to refer to a term `fugasity' in the case of
non-ideal gases. At high temperatures as it is common in metallurgy, gases are
near ideal and the the term fugasity is considered superfluous.
Dalton's law of Partial pressures states that the partial pressure of a gas `A',
p
A
, in a mixture of gases `A', `B', `C', etc., is given by
P
A
X
A
P (2.45)
where P is the total pressure of the gas mixture (P p
A
p
B
p
C
. . .) and X
A
is
the mole fraction of gas species A.
2.4.6 Ellingham diagrams
Consider the reaction betwee n metal M (s) and oxygen to form oxide MO
2
(s):
M O
2
MO
2
(2.46)
At equilibrium
G (G
products
ÿ G
reactants
) 0 (2.47)
54 Fundamentals of metallurgy
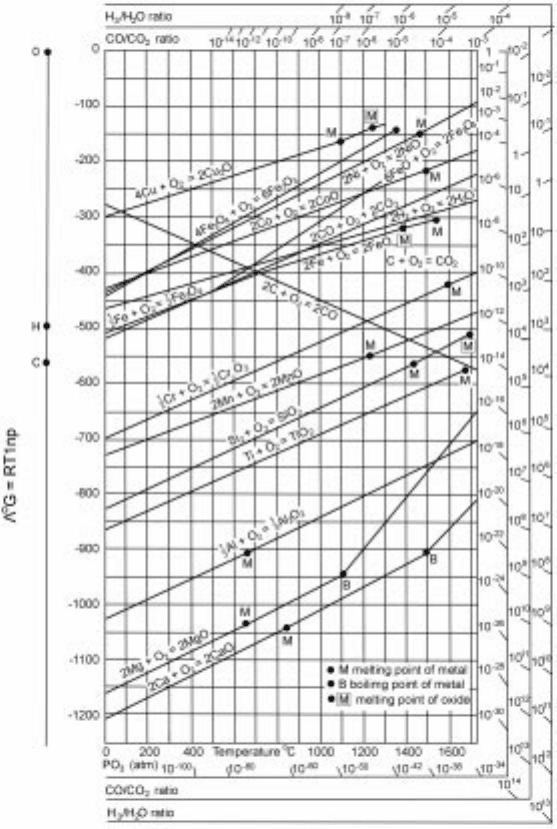
Assuming that the metal and the oxide phases are mutually insoluble and that
they are in their standard state, and, further remembering from equation (2.44),
that G
O2
= ëG
O2
+ RT ln p
O2
, equation (2.47) can be rewritten as
ëG
MO
2ÿ
(ëG
M
ëG
O
2
) ëG RT ln p
O
2
(2.48)
Figure 2.11 shows a plot of ëG as a function of temperature for a number of
metal±metal oxide systems. The stability of the oxide increases as we go down
2.11 Elligham diagram for oxides.
6
Thermodynamic aspects of metals processing 55
