Scheideler C. Universal Routing Strategies for Interconnection Networks

Подождите немного. Документ загружается.

3.4 Basic Definitions in Routing Theory 37

In case of online protocols, at the beginning every processor only knows

the messages that are currently stored in it (and, maybe, a few global para-

meters such as the size of the routing problem). In general, it makes no sense

to inform all processors about the whole routing problem before starting to

deliver the messages, since - as we will see - for many situations knowledge

about a small fraction of the routing problem already suffices for the proces-

sors to develop very efficient routing strategies. Note that online protocols

are also sometimes called local control or distributed protocols.

There are basically two classes of online protocols. In order to send a

message from its source to its destination in G it has to traverse a contigu-

ous sequence of links called routing path. Given a source-destination pair a

message may either have to traverse a path specified in advance or is able to

choose among several alternative paths depending on the source-destination

pairs of other messages or other events. The first case is called oblivious rout-

ing and the second case adaptive routing.

Oblivious Routing. In case of oblivious routing the path a message uses

only depends on its source and destination. Let Pv,w denote the path from v

to w in G that has to be taken by every message that wants to travel from

v to w. Then P = {Pv,~ I v,w E V} is called path system of size [VI. In this

case any routing problem 7~ can be defined by specifying a path collection

Pn of size [7~[ that contains the path Pv,w for every pair (v, w) in T~. Pn is

called

simple if no path in Pn contains the same edge more than once,

- shortcut-free if no piece of a path in Pn can be shortcut by any combination

of other pieces of paths in pn,

shortest if all paths in 7~n are shortest paths in G, and

- leveled if the nodes can be arranged in levels such that for every pair (v, w)

in 7~, the path from v to w in Pie only contains edges that lead from level

i to level i + 1 for some i _> 0.

The following relationship holds for these types of path collections.

leveled p. c. C shortest p. c. C shortcut-free p. c. C simple p. c.

Important parameters for the runtime are

- the size n of Pze, that is, the number of paths Pze contains,

the congestion C of Pn, that is, the maximal number of paths in P~ that

contain the same edge in G, and

- the dilation D of P~e, that is, the length of a longest path in Pze.

In case that we want to route random functions, we often use the notion

of expected congestion that is defined as follows. For an edge e and a path

system P, let the expected congestion Ce of e be defined as the expected

number of messages that traverse e using paths in P during the routing of a

randomly chosen (1-)function. The expected congestion of P is then defined

as 0 = maxoe Oe.

38 3. Terminology

Adaptive Routing.

In case of adaptive routing, the path a message uses

is not predetermined. There are several parameters that are used to measure

the performance of adaptive routing protocols: The bisection width, flux,

expansion, or routing number (see Chapter 5) of a network.

In adaptive protocols that do not restrict the messages to approach their

destinations via shortest paths, livelocks can happen. Messages are defined

to run into a livelock if they run infinitely often along the same cycle in the

network.

3.4.5 Space-Efficient Routing

In theory it is often assumed that we have unit size messages, unbounded

buffers, and enough space in the processors to store the protocol and routing

information such as routing tables that assign to each source-destination pair

a subset of links leaving that processor. In practice, however, messages are

only allowed to have a header of limited size (ATM-packets, e.g., only consist

of 53 bytes [B195]), buffers can only store a limited number of messages (or

even a limited number of parts of a message), and processors only have a

limited amount of space to store routing information. Within the field of

space-efficient routing there are two mainstreams.

Routing with Bounded Buffer Size

In networks with bounded buffers it may happen that messages prevent each

other from moving forward. Such a situation is called deadlock. It is a chal-

lenging task to find oblivious and adaptive protocols that run efficient and

can avoid deadlocks in case of bounded buffers. Protocols that do not require

any edge buffers to route the messages to their destinations are called hot

potato routing protocols.

Compact Routing

The theory of compact routing deals with questions about how a limited space

at the processors influences the efficiency of routing tables. It basically follows

two directions.

Relationship between Space and Stretch Factor.

The efficiency of a

routing scheme is measured in terms of its stretch factor, that is, the maxi-

mum ratio over all pairs of nodes between the length of a route produced by

the scheme and the length of a shortest path between these nodes. Let G be

an arbitrary network, and let v be any node in G. Given any s > 1, let Ss(G)

denote the class of all path selection strategies with stretch factor s in G.

For every strategy S E Ss(G), let MEM(v, S) be the memory requirement

in v to realize strategy S. Then we define, for every network G = (V, E) and

strategy S,

3.4 Basic Definitions in Routing Theory 39

the

global memory requirement

of S in G as

MEMg(G, S) = ~vey MEM(v, S),

and

the

local memory requirement

of S in G as

MEMt(G, S) = maxvey MEM(v, S).

Using this, we define, for every stretch factor s,

the

global memory requirement

of G as

MEMg(G, s) =

minses~(a)

MEMg(G, S),

and

- the

local memory requirement

of G as

MEMo(G, s) =

minses,(c)

MEMt(G, S).

It is interesting to consider both global and local memory requirements be-

cause it is possible that

MEMg(G, s)

nMEM~(G, s)

for some graph G and

stretch factor s. That is, informally, the global memory requirement does not

indicate whether the routing information can be evenly balanced between

all nodes. On the contrary, the local memory requirement does not indicate

whether all nodes need such a large memory.

The space for storing information in the headers of messages is usually

bounded to be at most logarithmic to the size of G.

Relationship between Space and Slowdown. Within this model the

efficiency of a routing scheme is measured in terms of its

slowdown,

that is,

the ratio between the worst case time to route any permutation in a network

using the scheme and the routing number of the network (see Section 5 for a

definition of the routing number). Given a slowdown s, the local and global

space requirements

MEMg(G, s) and MEMt(G, s)

of a scheme are measured

as defined for the stretch factor above.

4. Introduction to Store-and-Forward Routing

In the following six chapters we will concentrate on presenting store-and-

forward routing strategies. Such strategies are used on machines such as the

NCube, NASA MPP, Intel Hypercube, and Transputer-based machines. Since

the store-and-forward model assumes that all messages are of unit length, it

is the easiest and therefore the most studied model in the literature.

Let us start with giving an overview of results in the area of store-and-

forward routing, and describing networks for which optimal randomized and

deterministic store-and-forward routing protocols are already known. Chap-

ter 5 introduces a parameter called the routing number. This parameter will

be used extensively in the following chapters to apply routing protocols to ar-

bitrary networks. In Chapter 6 we prove the existence of three offline protocols

for routing packets along a fixed path collection and show, how these proto-

cols can be applied to network emulations. Chapter 7 gives an overview on the

best universal oblivious protocols for store-and-forward routing known so far.

It is shown, how each of these protocols can be applied to routing in specific

networks, and what the limitations of these protocols are. Chapter 8 gives

an overview on adaptive store-and-forward routing protocols, and describes

several techniques for developing universal adaptive protocols. It is further

demonstrated how efficiently these techniques can be applied to routing in

arbitrary networks. In Chapter 9 we show how a limited space for storing

routing information in the packets and the nodes of the network influences

the performance of routing algorithms. Both randomized and deterministic

protocols are developed that can be efficiently applied to arbitrary networks

even under severe space limitations.

4.1 History of Store-and-Forward

Routing

In this section we give an overview on results known about store-and-forward

routing in specific networks and universal oblivious store-and-forward routing

protocols.

42 4. Introduction to Store-and-Forward Routing

4.1.1 Routing in Specific Networks

In 1965, Bene~ [Be65] showed that the inputs and outputs of an N-node

Benew network (two back-to-back butterfly networks) can be connected in

any permutation by a set of disjoint paths. Shortly afterwards, Waksman

[Wa68] devised a simple sequential algorithm for finding the paths in O(N)

time. Given the paths, it is straightforward to route a set of packets from

the inputs to the outputs of an N-node Bene.~ network in any one-to-one

fashion in O (log N) steps using buffers of size 1. Although the inputs comprise

only O(N/logN) nodes in an N-node Bene~ network, it is possible to route

log N permutations from the inputs to the outputs in O(logN) steps by

routing the permutations one after the other in a continuous fashion (i.e.,

using pipelining). Unfortunately, no efficient parallel algorithm for finding

the paths is known.

In 1968, Batcher [Ba68] devised an elegant and practical parallel algorithm

for sorting N packets on an N-node shuffie-exchange network in log 2 N steps

using buffers of size 1. The algorithm can be used to route any permutation

of packets by sorting them according to their destination addresses. The

result extends to routing many-one problems provided that (as is typically

assumed) two packets with the same destination can be combined to form a

single packet should they meet en route to their destination.

No better deterministic algorithm was found until 1983, when Ajtai et al.

[AKS83] solved a classical open problem by constructing an O(log N)-depth

sorting network. Leighton [Le85] then used this O(N log N)-node network to

construct a degree 3 N-node network capable of solving any N-packet rout-

ing problem in O(log N) steps using buffers of size 1. Although this result is

optimal up to constant factors, the constant factors are quite large and the

algorithm is of no practical use. Hence, the effort to find fast deterministic

algorithms continued. In 1989, Upfal discovered an O(log N)-step algorithm

for routing on an expander-based network called multibutterfly [Up89]. The

algorithm solves the routing problem directly without reducing it to sorting,

and the constant factors are much smaller than those of the AKS-based algo-

rithms. In [LM92], Leighton and Maggs show that the multibutterfly is fault

tolerant and improve the constant factors in Upfal's analysis. Borodin et al.

[BRSU93] further show that any permutation can be routed deterministically

in an s-ary multibutterfly of size N in time O(log, N). Recently, Maggs and

VScking [MV97] found a constant degree variant of the multibutterfly that

allows every h-relation to be routed in O(h + log N) steps.

There has also been great success in the development of efficient ran-

domized packet routing algorithms. The study of randomized algorithms was

pioneered by Valiant [Va82] who showed how to route any permutation of

N packets in O(log N) steps on an N-node hypercube with buffers of size

O(log N) at each node. Valiant's idea was to route each packet to a randomly

chosen intermediate destination before routing it to its true destination. Al-

though the algorithm is not guaranteed to deliver all packets within O(log N)

4.1 History of Store-and-Forward Routing 43

steps, for any permutation it does so with high probability. In particular, the

probability that the algorithm falls to deliver the packets within O(logN)

steps is at most

1/N k,

for any constant k > 0. (The value of k can be made

arbitrarily large by increasing the constant in the O(log N) bound.) In the

following, we use the term "w.h.p." (with high probability) whenever we have

a probability of at least 1 -

1/N k

for any constant k > 0.

Valiant's result was improved in a succession of papers by Aleliunas [A182],

Upfal [Up82], Pippenger [Pi84], and Ranade [Ra87]. Aleliunas and Upfal de-

veloped the notion of a

delay path

and showed how to route on the shuffle-

exchange and butterfly of size N in O(log N) steps, w.h.p., using buffers of

size O(log N). Pippenger was the first to eliminate the need for large buffers,

and showed how to route on a variant of the butterfly in O(logN) steps,

w.h.p., with buffers of size O(1) [Pi84]. Ranade showed how combining can

be used to extend the Pippenger result to include many-one routing problems,

and tremendously simplified the analysis required to prove such a result. As

a consequence, it has finally become possible to simulate a step of an N-

processor CRCW PRAM on an N-node butterfly or hypercube in O(log N)

steps, w.h.p., using constant-size buffers on each edge [Ra87]. Borodin

et al.

[BRSU93] further showed that any permutation can be routed in any s-ary

butterfly of size N in time O(log s N), w.h.p.

Concurrent with the development of these hypercube-related packet rout-

ing algorithms has been the development of algorithms for routing in meshes.

The randomized algorithm of Valiant and Brebner can be used to route

any permutation of N packets on a (v/-N, 2)-mesh in O(v/-N) steps using

buffers of size O(log N). Kunde [Ku88] showed how to route deterministi-

cally in (2 + e)v/-N steps using buffers of size O(1/e). Krizanc

et al.

[KRT88]

showed how to route any permutation in 2v/-N + O(log N) steps, w.h.p., us-

ing constant-size buffers. Furthermore, Leighton

et al.

[LMT89] discovered a

deterministic algorithm for routing any permutation in 2v/N- 2 steps using

constant-size buffers, thus achieving the optimal time bound in the worst

case. In case of d-dimensional meshes, the results by Kunde [Ku91] and Suel

[Su94] imply that there is a deterministic protocol for routing any permuta-

tion in optimal time using constant size buffers. Kaklamanis

et al.

[KKR93a]

present a randomized hot-potato protocol that routes any permutation and

randomly chosen function in a d-dimensional torus of side length n in time

d. n + O(log 2 n), w.h.p.

4.1.2 Universal Routing

In the last years, also

universal

routing protocols have been developed, that is,

protocols that can be used for any communication pattern in any network.

The advantage of these protocols is that they can be quickly adapted to

topology changes that occur if new processors are added or some break down.

In 1988, Leighton

et al.

[LMR88] showed that for any simple path collection

with congestion C and dilation D there is an offline routing scheme that

44 4. Introduction to Store-and-Forward Routing

routes a packet along each of the paths in time

O(C + D)

using (sufficiently

large) constant size edge buffers. In case that only buffers of size 1 are allowed,

Meyer anf der Heide and Scheideler [MS95b] showed that packets can be

routed offiine along an arbitrary simple path collection with congestion C and

dilation D in time

O((D+C

log(C+D) log log(C+D))(log log log(C+D))

TM)

for any constant e > 0.

Several results about online universal protocols have also been found.

Leighton

et al.

[LMR88] presented an online protocol for routing packets in

any simple path collection of size n with congestion C and dilation D in time

O(C + D

log(nD)), w.h.p. In another paper, Leighton

et al.

[LMRR94] used

the techniques in IRa87] to develop an online protocol that can route packets

along any leveled path collection of size n with depth D and congestion C

in time

O(C + D +

logn), w.h.p, using constant size buffers. Meyer auf der

Heide and VScking [MV95] presented a protocol that can route packets along

any shortcut-free path collection of size n with congestion C and dilation

D in time

O(C + D +

logn), w.h.p., using buffers of size C. Cypher

et al.

[CMSV96] developed two randomized protocols for arbitrary simple path

collections. The first protocol runs in time

O((D

log log n + C + log

n.log log

n ~.

log log(C.D) /

log(C.D)

loglog(C.D)/, w.h.p., and requires buffers of size 8(log(C.D)

log log(C.D)/" The second

protocol runs in time

O(C. D 1/B +

Dlogn), w.h.p., if buffers of size B are

available. Furthermore, Rabani and Tardos [RT96] showed that there is a

randomized protocol for arbitrary simple path collections that runs in time

O(C) + (log* n)O(Iog" n)D+poly (log n), w.h.p., using buffers of size

poly(log

n).

Recently, Ostrovsky and Rabani [OR97] presented a randomized protocol for

arbitrary simple path collections that runs in time

O(C + D +

log 1+~ n) for

any constant e > 0, w.h.p., using buffers of size

poly(logn).

Meyer auf der Heide and Scheideler [MS96a] developed a universal deter-

ministic routing protocol. They showed, for instance, that for any network

with sufficiently large diameter (such as the class of planar networks), this

protocol reaches the best possible worst case time for routing arbitrary per-

mutations. A detailed description of the universal protocols mentioned above

will be given in Chapters 6 to 8.

4.2 Optimal Networks for Permutation Routing

Consider an arbitrary network of size N with degree d. Clearly, since

the

diameter of any graph of size N with degree d is at least log d N, there exists

a permutation that takes at least log d N steps to be routed. The question

is whether there are networks that can reach this lower bound up to con-

stants. In the following we describe two classes of networks that either have

an optimal randomized routing protocol or an optimal deterministic routing

protocol.

4.2 Optimal Networks for Permutation Routing 45

4.2.1 Optimal Networks for Randomized Routing

In this section we show that for any d _> 4 there exists a network of size N with

degree d such that there is a randomized protocol for routing an arbitrary

permutation in optimal time

O(logdN),

w.h.p. For this we introduce the

s-ary butterfly.

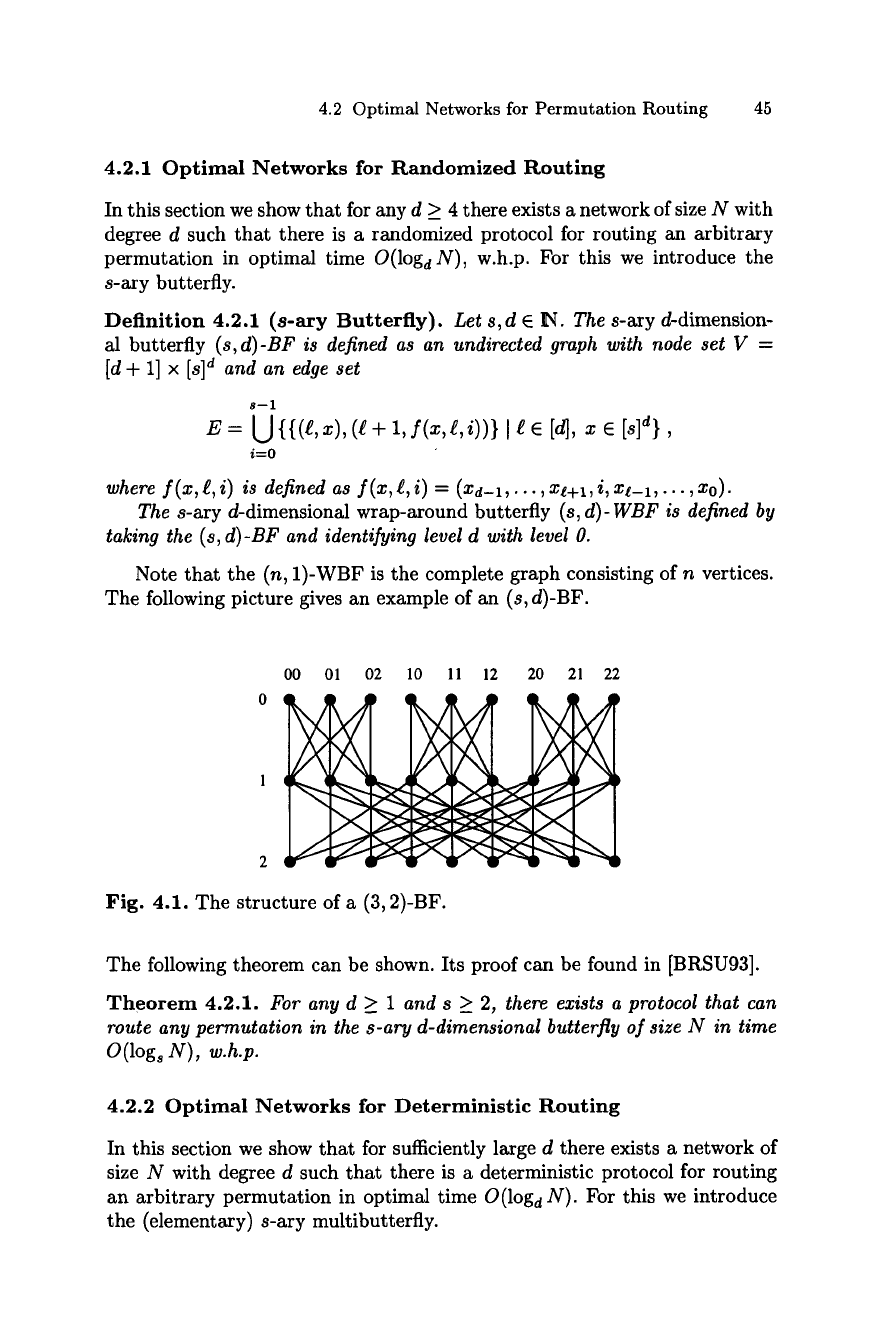
Definition 4.2.1 (s-ary Butterfly).

Let s, d E ~. The s-ary

d-dimension-

al butterfly

(s, d)-BF is defined as an undirected graph with node set V =

[d + 1] x

Is] d and an edge set

s--1

E = U {{(~'x)'(~d- 1, f(x,~,i))} I ~ e [d], x e [8]d},

i=0

where f(x, e, i) is defined as f(x,

~, i) = (Xd-l,..., X~+I, i, Xt-1,. 9 -, X0).

The

s-ary d-dimensional wrap-around butterfly (s,

d)- WBF is defined by

taking the

(s,

d)-BF and identifying level d with level O.

Note that the (n, 1)-WBF is the complete graph consisting of n vertices.

The following picture gives an example of an (s, d)-BF.

\/N

O1 02 10 11 12 20 21 22

,,--/. Y/

//X

Fig. 4.1. The structure of a (3, 2)-BF.

The following theorem can be shown. Its proof can be found in [BRSU93].

Theorem 4.2.1.

For any d >_ 1 and s > 2, there exists a protocol that can

route any permutation in the s-ary d-dimensional butterfly of size N in time

O(log s

N), w.h.p.

4.2.2 Optimal Networks for Deterministic Routing

In this section we show that for sufficiently large d there exists a network of

size N with degree d such that there is a deterministic protocol for routing

an arbitrary permutation in optimal time O(log d N). For this we introduce

the (elementary) s-ary multibutterfly.

46 4. Introduction to Store-and-Forward Routing

The basic building block of the s-ary multibutterfly is an

s-ary m-splitter

(see [BRSU93]).

The s-ary m-splitter (or (s, m)-splitter) is a bipartite graph with m input

nodes and m output nodes. In this graph the output nodes are partitioned

into v~ output sets, each with

m/vfs

nodes. Every input node has 2 ~ edges

to each of the v/s output sets. The edges connecting the input set to each

of the output sets define an expander graph with properties described in

[BRSU93].

The

s-ary d-dimensional multibutterfly (s,

d)-MBF has d + 1 levels. The

vertices at level 0 < i < d - 1 are partitioned into v~ sets of

mi = V ~d-i

consecutive nodes. Each of these sets in level i is an input set of an s-ary

mi-splitter. The output sets of that splitter are v/s sets of size

mi+l

in level

i + 1. Thus each node in the (s, d)-MBF is the endpoint of at most 2. ~ = s

edges. Figure 4.2 shows the structure of a (16, d)-MBF.

level n nodes

0[ f

. . ~ 9 9 9 9 ~ ~ 9 9 9

Fig. 4.2. The structure of a (16, d)-MBF.

Using the (s, d)-MBF, the following result can be shown. Its proof can be

found in [BRSU93].

Theorem

4.2.2.

For sufficiently large s, the s-ary multibutterfly of size N

can route any permutation from the inputs to the outputs in time

O(log s N).

Using techniques in [Up92], the s-ary multibutterfly can be extended to

route any global permutation in O(log s N) steps.

5. The Routing Number

In the following chapters we will often refer the routing time needed by our

online routing protocols to the worst case routing time of a best offiine routing

algorithm, the so-called

routing number.

This number is defined as follows

(see, e.g., [ACG94, MS96a]):

Consider an arbitrary network G with N nodes and link bandwidth one.

For a permutation ~ E

SN,

let

R(G, ~)

be the minimum possible number of

steps required to route packets offline in G according to r using the multi-

port model with unbounded buffers. Then the

routing number R(G)

of G is

defined by

R(G) = max n(G,~r) .

,r6SN

In case that there is no risk of confusion about the network G we will write

R instead of

R(G).

The routing number has the following nice property.

Theorem 5.0.3.

For any network G with routing number R and any routing

strategy, the average number of steps to route a permutation in G is bounded

by ~(R).

Proof.

Let/~ = 1

~']~esN R(G, r)

denote the average number of steps to

route a permutation in G using the best possible routing strategy. Consider

any fixed permutation ~r. In order to bound the minimum number of steps

to route ~r we will use a probabilistic argument based on Valiant's trick (see

[Va82]) by first sending the packets to random intermediate destinations be-

fore sending them to the destinations prescribed by 7r. Let X be a random

variable denoting the minimum number of steps necessary to route a ran-

domly chosen permutation. According to the Markov Inequality it holds:

Pr[X > 3/~1 < 89 .

Therefore, for a randomly chosen permutation ~ for the intermediate des-

tinations, it holds that the minimum number of steps to route the packets

first to their intermediate destinations (prescribed by ~) and then to their

final destinations (prescribed by r) is at least 6/~ with probability at most

1 + 1 < 1. Therefore there exists an offiine protocol that routes r in at most

3_ 3

6R steps. Thus R < 6/~, which completes the proof. []